
第一章 逻辑代数基础 1.2逻辑函数的化简方法 L.2.1逻辑函数的标准与或式和最简式 、标准与或表达式 Y=F(A,B,C) 标准与 或式 ABC+ABC+ABC+ABC 最小项 标准与或式就是最小项之和的形式
一、标准与或表达式 Y = F ( A ,B ,C ) = ABC + ABC + ABC + ABC 1. 2 逻辑函数的化简方法 1. 2. 1 逻辑函数的标准与或式和最简式 标准与 或式 标准与或式就是最小项之和的形式 最小项

第一章 逻辑代数基础 最小项的概念: 包括所有变量的乘积项,每个变量均以原变量或 反变量的形式出现一次。 Y=F(A,B) (2变量共有4个最小项 ABABABAB /=F(A,B,C)(3变量共有8个最小项) ABC ABC ABCABC ABCABCABC ABC (1变量共有2"个最小项)
1. 最小项的概念: 包括所有变量的乘积项,每个变量均以原变量或 反变量的形式出现一次。 Y = F ( A ,B ) ( 2 变量共有 4 个最小项) AB AB AB AB ( n 变量共有 2 n个最小项) Y = F ( A ,B ,C ) ( 3 变量共有 8 个最小项) ABC ABC ABC ABC ABC ABC ABC ABC
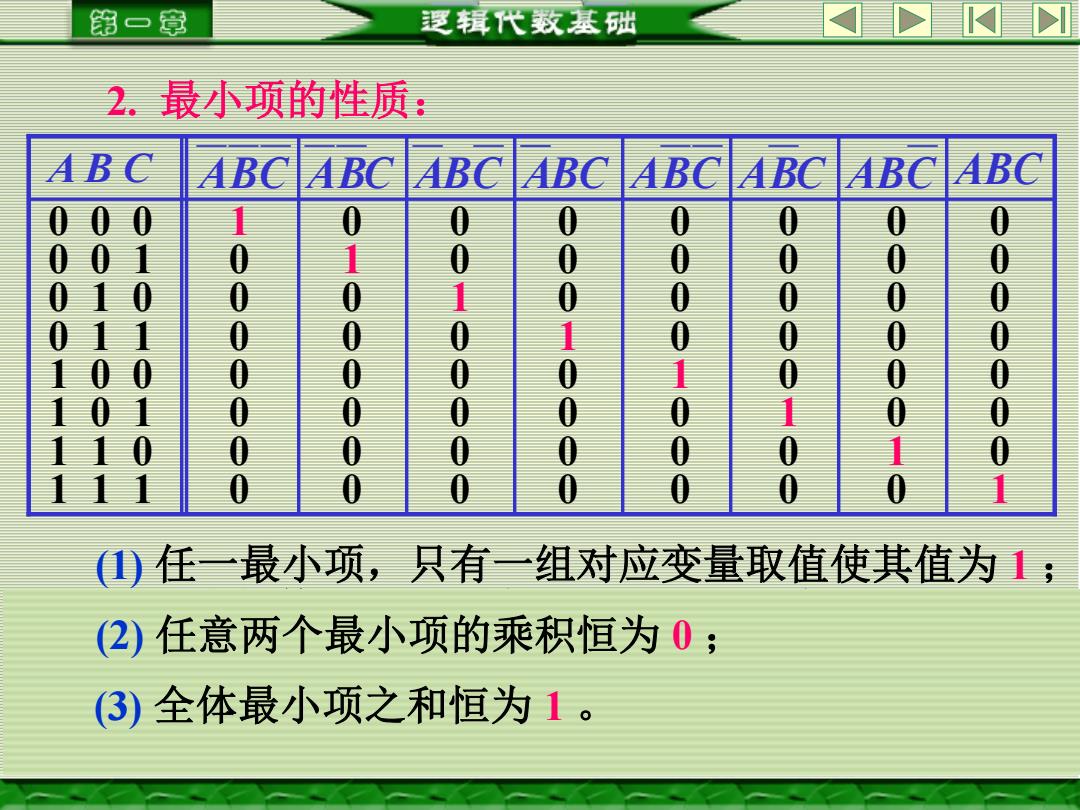
第一章 逻辑代数基础 2.最小项的性质: B ABC BC ABC ABC ABC ABC ABC ABC 0 0 0 0 0 0 0 0 0 0 0 0 0 0 01 0 0 0 0 0 0 0 0 0 0 0 ()任一最小项,只有一组对应变量取值使其值为; (2)任意两个最小项的乘积恒为0; 3)全体最小项之和恒为1
对应规律:1 原变量 0 反变量 2. 最小项的性质: 0 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 A B C ABC ABC ABC ABC ABC ABC ABC ABC (1) 任一最小项,只有一组对应变量取值使其值为 1 ; (2) 任意两个最小项的乘积恒为 0 ; (3) 全体最小项之和恒为 1
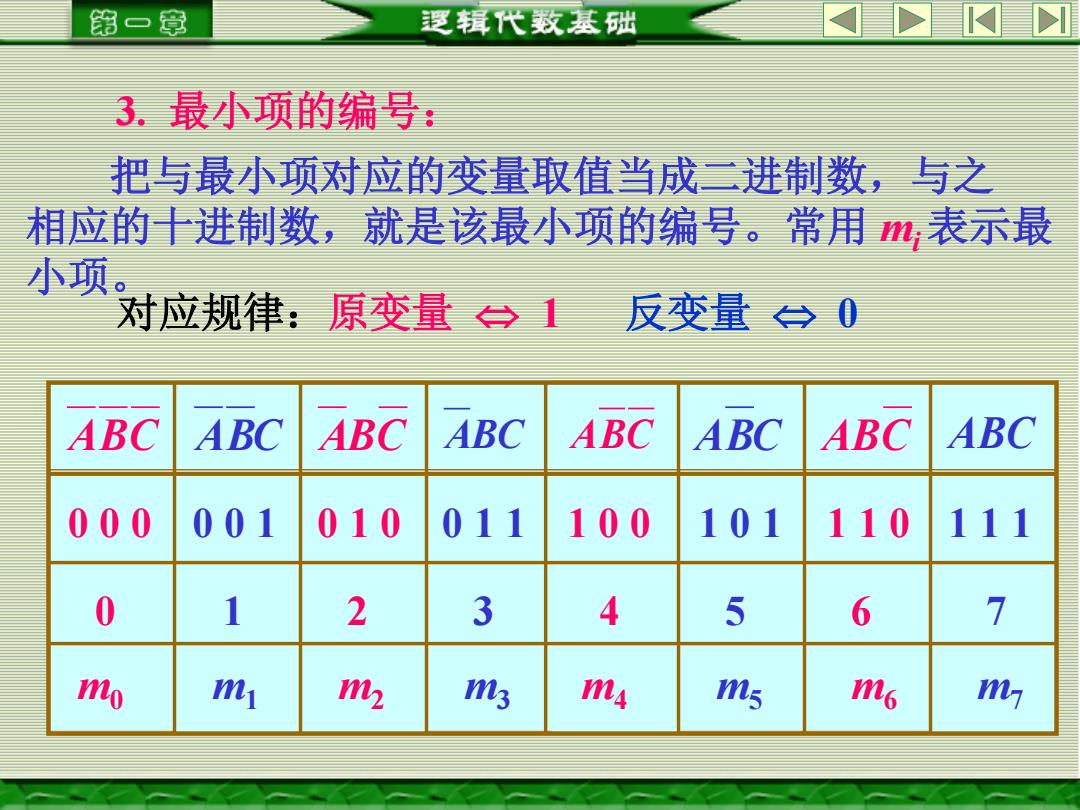
第一章 逻辑代数基础 3.最小项的编号: 把与最小项对应的变量取值当成二进制数,与之 相应的十进制数,就是该最小项的编号。常用m,表示最 小项 对应规律:原变量令1 反变量台0 ABC ABC ABC ABC ABC ABC ABC ABC 000 001 010 011 100 101 110 111 0 1 2 3 4 5 6 7 o 2 3 ms ms m6 M
3. 最小项的编号: 把与最小项对应的变量取值当成二进制数,与之 相应的十进制数,就是该最小项的编号。常用 mi 表示最 小项。 对应规律:原变量 1 反变量 0 ABC ABC ABC ABC ABC ABC ABC ABC 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 2 3 4 5 6 7 m0 m1 m2 m3 m4 m5 m6 m7

第一章 逻辑代数基础 4.最小项是组成逻辑函数的基本单元 任何逻辑函数都是都可以表示成最小项和的形式。 且表达式唯一。 [例们写出下列函数的标准与或式: Y=F(A,B,C)=AB+AC 解]Y=AB(C+C)+AC(B+B =ABC+ABC+ABC+ABC 6 店 g =m。+m,+41+L3 或=∑m(自,3,6,7
4. 最小项是组成逻辑函数的基本单元 Y = F( A ,B ,C ) = AB + AC = ABC + ABC + AB C + ABC = m6 + m7 + m1 + m3 = m (1 , 3 , 6 , 7) 任何逻辑函数都是都可以表示成最小项和的形式。 且表达式唯一。 Y = AB(C +C) + AC(B + B) [例] 写出下列函数的标准与或式: [解] 或 m6 m7 m1 m3

第一章 逻辑代数基础 标准与或表达式可由真值表直接写出P1门下部。 [例们写出的标准与或表达式。 B F=AB+AB*AB
标准与或表达式可由真值表直接写出(P17下部)。 [例] 写出F的标准与或表达式。 A B F 0 0 0 1 1 0 1 1 0 1 1 1 F AB AB AB = + +

数字电子技术 作业 P68思考题与习题 1.4(1)、1.5(3)、 1.7Y4、1.8(1)
作业 P68 思考题与习题 1.4(1)、 1.5(3)、 1.7 Y4 、 1.8(1)

第一章 逻辑代数基础 逻辑函数的最简表达式 ·最简与或表达式:与项的个数最少,每个与项中 的变量个数也最少的与或表达式。 ·如 Y=F(A,B)=AB+AB+AB =A十B 其他表达 式 Y=AB.AC 与非与非 Y=(A+C(A+B) 或与或与 Y=A+C+A+B 或非或排非
二、逻辑函数的最简表达式 • 最简与或表达式:与项的个数最少,每个与项中 的变量个数也最少的与或表达式。 • 如 ( , ) Y F A B AB AB AB = = + + Y AB AC = (A C)(A B) Y = + + A C A B Y = + + + 其他表达 式: 与非与非 或与或与 或非或非 = + A B

第一章 逻辑代数基础 L.2.2逻辑函数的公式化简法 公式 (与或式 最简与或式) 定理 一、并项法: AB+AB=A [例]Y-ABC+ABC+AB BVBABMB3333939791 83808888 书p20) =AB+AB=B 例]Y-ABC+ABC+ABC+ABC =A(BC+BC)+A(BC+BC) =AB⊕C+AB⊕C A
1. 2. 2 逻辑函数的公式化简法 一、并项法: AB + AB = A Y = ABC + ABC + AB = AB + AB = B Y = ABC + ABC + ABC + ABC = A (BC + B C) + A (BC + BC) = A = A B C + A(B C) [例 ] (书 p20) [例] (与或式 最简与或式) 公式 定理

第一章 逻辑代数基础 二、吸收法: A+AB=A [例们Y=AB+AD+BE (书p20) =A+B+AD+BE=4+B a03822 L例们Y=AB+ACD+BCD 1888838888 =AB+(4+B)CD =AB+ABCD=AB=A+B
二、吸收法: A + AB = A Y = AB + AD + BE = A + B + AD + BE = A+ B [例] (书 p20) [例] Y = AB + ACD + BCD = AB + (A + B) CD = AB + AB CD = AB = A + B