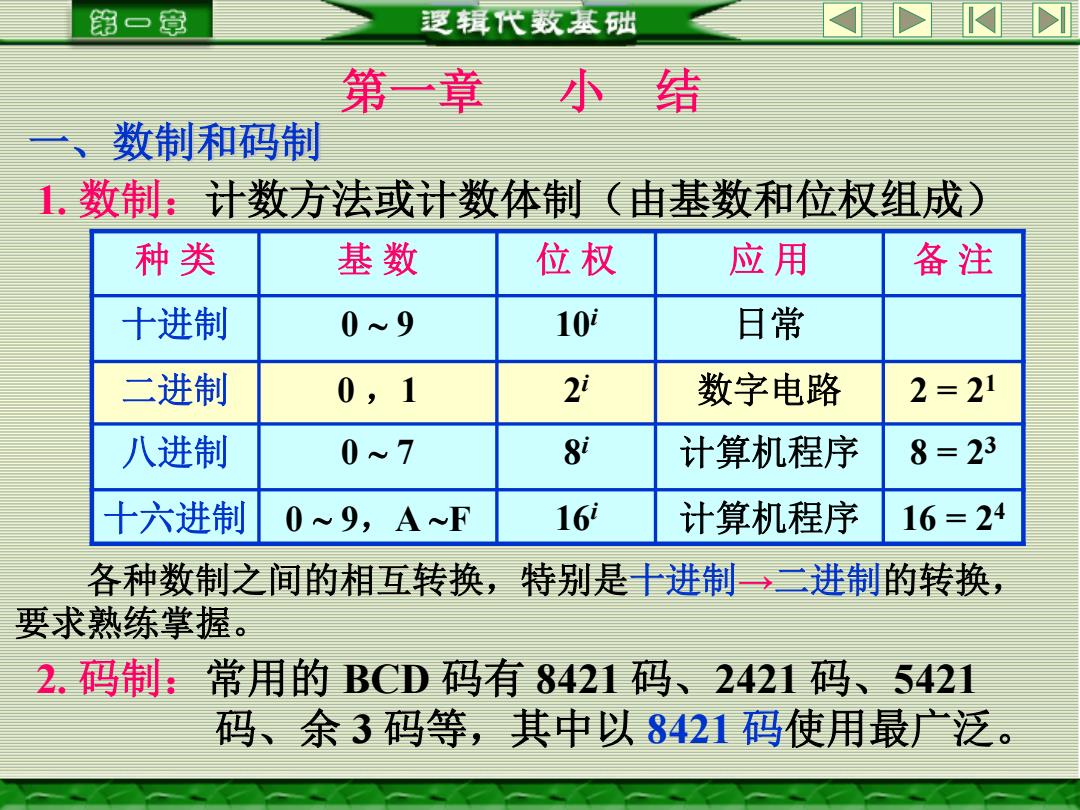
第一章 逻辑代数基础 第一章小结 、 数制和码制 1.数制:计数方法或计数体制(由基数和位权组成) 种类 基数 位权 应用 备注 十进制 0~9 10 日常 二进制 0,1 21 数字电路 2=21 八进制 0~7 81 计算机程序 8=23 十六进制 0心9,A~F 16 计算机程序 16=24 各种数制之间的相互转换,特别是十进制一→二进制的转换, 要求熟练掌握。 2.码制:常用的BCD码有8421码、2421码、5421 码、余3码等,其中以8421码使用最广泛
第一章 小 结 一、数制和码制 1. 数制:计数方法或计数体制(由基数和位权组成) 种 类 基 数 位 权 应 用 备 注 十进制 0 9 10i 日常 二进制 0 ,1 2 i 数字电路 2 = 21 八进制 0 7 8 i 计算机程序 8 = 23 十六进制 0 9,A F 16i 计算机程序 16 = 24 各种数制之间的相互转换,特别是十进制→二进制的转换, 要求熟练掌握。 2. 码制:常用的 BCD 码有 8421 码、2421 码、5421 码、余 3 码等,其中以 8421 码使用最广泛

第一章 逻辑代数基础 练习]完成下列数制和码制之间的相互转换 32。。4。 1.(37)o=(100101 02=(45)3=(25)1 V-1-1952 32821 2.(53)=101011 )2=(43)0=(2B) 5121286416842 3.(2DE)6=(101011110)2=(734)0 12816421 4.(151).=(10010111D2=(000101010001 8421BCD 684 5.(101001 842BcD=(29 10
[练习] 完成下列数制和码制之间的相互转换 8 2 10 16 2. ( 53 ) ( 101 0 11 ) ( ) ( ) 10 2 8421BCD 4. ( 151 ) ( ) ( ) 128 16 4 2 1 0001 0101 0001 16 2 10 3. ( 2DE) ( ) ( ) 8421BCD D B 5. (10 10 01) ( ) ( ) 10 1101 1110 29 11101 512 128 64 16 8 4 2 10 010111 32 8 2 1 43 10 2 8 16 1. ( 37 ) ( 10 0 101 ) ( ) ( ) 32 4 1 45 25 2B734 16 8 4 1

第一章 逻辑代数基础 二、常用逻辑关系及运算 L.三种基本逻辑运算:与、或、非 2.四种复合逻辑运算:与非、或非、与或非、异或 真值表 函数式 逻辑符号 三、逻辑代数的公式和定理 是推演、变换和化简逻辑函数的依据,有些与普通代数相 同,有些则完全不同,要认真加以区别。这些定理中,摩根定 理最为常用。 练习求下列函数的反函数(用摩根定理),并化简。 Y-A·B+C+AD 解Y=A.B+C+AD=AB+C·AD=(A+B+C)(A+D AD+AB+BD+AC+CD=AD+AB+AC
二、常用逻辑关系及运算 1. 三种基本逻辑运算:与 、或、非 2. 四种复合逻辑运算:与非 、或非、与或非、异或 三、逻辑代数的公式和定理 是推演、变换和化简逻辑函数的依据,有些与普通代数相 同,有些则完全不同,要认真加以区别。这些定理中,摩根定 理最为常用。 真值表 函数式 逻辑符号 [练习] 求下列函数的反函数(用摩根定理),并化简。 Y A B C AD [解] Y A B C AD A B C AD (A B C)(A D) AD AB BD AC CD AD AB AC

第一章 逻辑代数基础 四、逻辑函数的化简法 化简的目的是为了获得最简逻辑函数式,从而使逻辑电路 简单、成本低、可靠性高。化简的方法主要有公式化简法和图 形化简法两种。 1.公式化简法 可化简任何复杂的逻辑函数,但要求能熟 练和灵活运用逻辑代数的各种公式和定理, 并要求具有一定的运算技巧和经验。 2.图形化简法:简单、直观,不易出错,有一定的步骤和 方法可循。但是,当函数的变量个数多于 六个时,就失去了优点,没有实用价值。 约束项: 可以取O,也可以取1,它的取值对逻辑函 (无关项) 数值没有影响,应充分利用这一特点化简 逻辑函数,以得到更为满意的化简结果
四、逻辑函数的化简法 化简的目的是为了获得最简逻辑函数式,从而使逻辑电路 简单、成本低、可靠性高。化简的方法主要有公式化简法和图 形化简法两种。 1. 公式化简法:可化简任何复杂的逻辑函数,但要求能熟 练和灵活运用逻辑代数的各种公式和定理, 并要求具有一定的运算技巧和经验。 2. 图形化简法:简单、直观,不易出错,有一定的步骤和 方法可循。但是,当函数的变量个数多于 六个时,就失去了优点,没有实用价值。 约束项: (无关项) 可以取 0,也可以取 1,它的取值对逻辑函 数值没有影响,应充分利用这一特点化简 逻辑函数,以得到更为满意的化简结果

第一章 逻辑代数基础 [练习]用公式法将下列函数化简为最简与或式。 (1Y=ABC+ABD+BE+DE+AD)B =B十AC+AD+E+DE+AD+B 阳 (2)Y=AC+BC+BD+CD+A(B+C)+ABCD+ABDE =AC+BC+BD+CD+A BC+ABDE AC+BC+BD+CD+A+ABDE ananaa7aa 10300 =A+BC+BD+CD 49393939399393939393939 3992999393934 =A+BC+BD
(1)Y ABC ABD BE (DE AD) B B AC AD E DE AD B 1 [练习] 用公式法将下列函数化简为最简与或式。 (2)Y AC BC BD CD A(B C) ABCD ABDE AC BC BD CD A BC ABD E A BC BDCD A BC BD AC BC BDCD A ABDE

第一章 逻辑代数基础 [练习用图形法将下列函数化简为最简与或式。 1.Y=ABCD+AB+ABD+BC+BCD 38888888888888 [解(①)画函数的卡诺图 (2)合并最小项:画包围圈 (3)写出最简与或表达式Y=AD+BD+CD CD AB 00011110 00 01 AD CD 10 BD
[练习] 用图形法将下列函数化简为最简与或式。 (1) 画函数的卡诺图 (2) 合并最小项:画包围圈 (3) 写出最简与或表达式 1. Y ABCD AB ABD BC BCD AB CD 00 01 11 10 00 01 11 10 1 1 1 1 1 1 1 1 BD AD CD Y AD BDCD [解] 1 1

第一章 逻辑代数基础 2.F(A,B,C,D) =∑0,1,2,8,9)+∑0,1且,12,13,14,5) 解()画函数的卡诺图 CD AB 00011110 (2)合并最小项: 00 0 画包围圈 BD (3)写出最简与或 X 表达式 10 Y=BC+BD ∑(0,12,3,145)=0
m d F A , B ,C , D ( 0 1 2 8 9 ) ( 10 11 12 , 13 14 15 ) 2. ( ) ,,,, , , , , (1) 画函数的卡诺图 (2) 合并最小项: 画包围圈 (3) 写出最简与或 表达式 AB CD 00 01 11 10 00 01 11 10 1 BC BD Y BC BD [解] 1 1 1 1 ╳ ╳ ╳ ╳ ╳ ╳ ( 10 11 12 , 13 14 15 ) 0 d , , ,

第一章 逻辑代数基础 五、逻辑函数常用的表示方法: 真值表、卡诺图、函数式、逻辑图和被形图。 它们各有特点,但本质相同,可以相互转换。尤 其是由真值表→逻辑图和逻辑图→真值表,在逻 辑电路的分析和设计中经常用到,必须熟练掌握
五、逻辑函数常用的表示方法: 真值表、卡诺图、函数式、逻辑图和波形图。 它们各有特点,但本质相同,可以相互转换。尤 其是由真值表 → 逻辑图 和 逻辑图 → 真值表, 在逻 辑电路的分析和设计中经常用到,必须熟练掌握