
电子科学与应用物理学标 电子科学与应用物理学标 组合逻辑电路 ·概述 第四章组合逻辑电路 ■组合逻辑电路分析 ■组合逻辑电路设计 梁华国 ·考虑特殊问题的逻辑设计 电子科学与技术系 ·若干常用的组合逻辑电路 http://dwxy.hfut.edu.cn/ ■组合逻辑电路中的竟争冒险 ⊙个北三生秋置 ⊙个北51热8 ② 电子科学与应用物理学网 电子科学与应用物理学松 概述 组合逻辑电路 组合逻辑电路的定义: ■概述 ·是指电路在任何时刻产生的稳定输出信号,仅 ·组合逻辑电路分析 取决于该时刻电路的输入信号。 ■组合逻辑电路设计 12 1=faa2…a.) ■若干常用的组合逻辑电路 J2=f5(aa2…a.) ■考虑特殊问题的逻辑设计 ·组合逻辑中竟争冒险 组合逻辑电路的框图 yw=faa2…a ·常用的中规模组合逻辑标准构件 ⊙个化大人 ⊙个也二1法行 电子科学与应用物理学院 组合逻辑电路分析 ② 电子科学与应用物理学酸 组合逻辑电路分析 一般分析步骤: 分析下图逻辑功能 ■阅读组合逻辑电路图 S=P·P2=P+P=AB+AB ■列写逻辑表达式 C=P]=AB ■列出真值表 HA P 001 0 ■指出电路的逻辑功能 01 1 半加器 ■做出对逻辑电路图的评价和改进 o S=A⊕B ⊙个工A号 ⊙个人香 1
1 电子科学与应用物理学院 School of Electronic Science & Applied Physics 梁华国 电子科学与技术系 http://dwxy.hfut.edu.cn/ 第四章 组合逻辑电路 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 考虑特殊问题的逻辑设计 若干常用的组合逻辑电路 组合逻辑电路中的竟争-冒险 电子科学与应用物理学院 School of Electronic Science & Applied Physics 概 述 组合逻辑电路的定义: 是指电路在任何时刻产生的稳定输出信号,仅 取决于该时刻电路的输入信号。 组合逻辑 电路 1 a a2 n a 1y 2 y my 组合逻辑电路的框图 y f (a a a ) y f (a a a ) y f (a a a ) m m n n n 1 2 2 2 1 2 1 1 1 2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 若干常用的组合逻辑电路 考虑特殊问题的逻辑设计 组合逻辑中竟争冒险 常用的中规模组合逻辑标准构件 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 一般分析步骤: 阅读组合逻辑电路图 列写逻辑表达式 列出真值表 指出电路的逻辑功能 做出对逻辑电路图的评价和改进 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 P1 P2 P3 s=P1• P2= P1+ P2 = AB+AB c=P3=AB A B s c 0 0 0 0 0 1 1 0 1 0 1 0 1 1 0 1 s= A B 分析下图逻辑功能 HA s c A B 半加器 s c • • B B A A
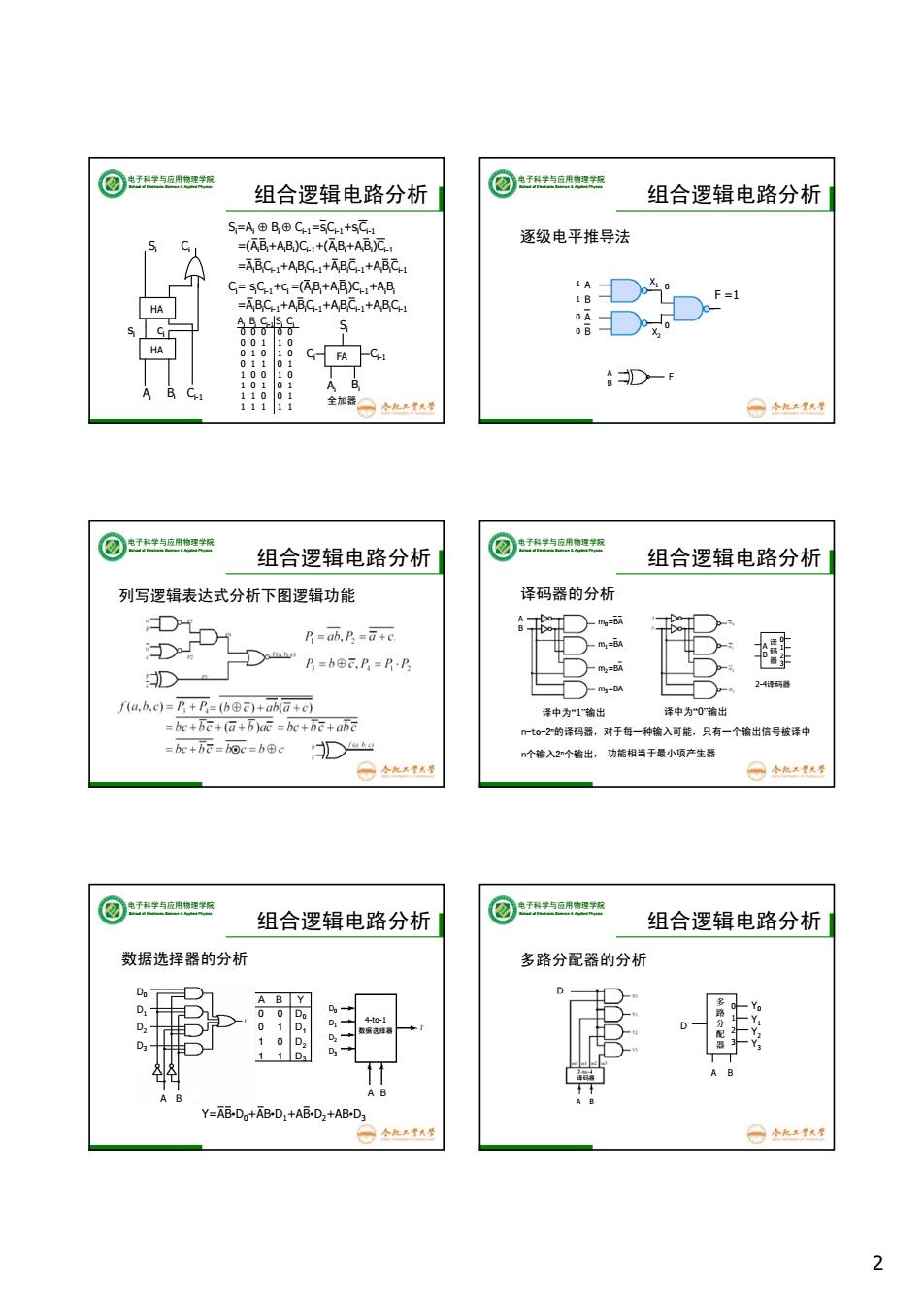
电子科学与应用物理学标 组合逻辑电路分析 ② 组合逻辑电路分析 S=A⊕B,DC1=sC1+sC =(AB+AB)C+(B+AB)C 逐级电平推导法 -ABC1+ABC1+ABC1+ABC C=sC:+G=(AB+AB)C+AB HA =ABC1+ABC+ABC+ABC 1B HA 0 A B D-F 全加器 ⊙个北51热8 ② 电子科学与应用物理学网 组合逻辑电路分析 电子科学与应用物理学粉 组合逻辑电路分析 列写逻辑表达式分析下图逻辑功能 译码器的分析 DH D D P=ab.P=G+c -BA P=b⊕元P=RE -BA D m=BA 2-4译码 fa,b,c)=乃+F=(h⊕c)+abMa+c 译中为“1”输出 译中为0输出 =be+be+(a+b)ac =be+he+abe mt0-2的译码器,对于每一种输入可能,只有一个输出信号被译中 =bc+BE=o=b⊕c D n个输入2n个输出,功能相当于最小项产生器 ○公化天达 ⊙个也去量 电子科学与应用物理学院 电子科学与应用物理学酸 组合逻辑电路分析 ② 组合逻辑电路分析 数据选择器的分析 多路分配器的分析 AB Y 0 00 D 4to-1 0 1 D3 Y=AB-D+AB-D,+AB-D2+AB-D3 2
2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 HA si ci Ai Bi HA Si Ci Ci-1 Si =Ai Bi Ci-1=si Ci-1+si Ci-1 =(Ai Bi +Ai Bi )Ci-1+(Ai Bi +Ai Bi )Ci-1 =Ai Bi Ci-1+Ai Bi Ci-1+Ai Bi Ci-1+Ai Bi Ci-1 Ci = si Ci-1+ci =(Ai Bi +Ai Bi )Ci-1+Ai Bi =Ai Bi Ci-1+Ai Bi Ci-1+Ai Bi Ci-1+Ai Bi Ci-1 0 0 0 0 0 0 0 1 1 0 0 1 0 1 0 0 1 1 0 1 1 0 0 1 0 1 0 1 0 1 1 1 0 0 1 1 1 1 1 1 Ai Bi Ci-1 Si Ci Ci FA Ci-1 Si Ai Bi 全加器 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 逐级电平推导法 A B F A B A B X1 X2 F =1 0 1 1 0 0 0 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 列写逻辑表达式分析下图逻辑功能 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 译码器的分析 A B m0=BA m1=BA m2=BA m3=BA 译中为“1”输出 译中为“0”输出 n-to-2n的译码器,对于每一种输入可能,只有一个输出信号被译中 译 码 器 A B 0 1 2 3 2-4译码器 n个输入2n个输出, 功能相当于最小项产生器 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 数据选择器的分析 D0 D1 D2 D3 0 0 0 1 1 0 1 1 A B Y D0 D1 D2 D3 A B Y=AB•D0+AB•D1+AB•D2+AB•D3 D0 D1 D2 D3 数据选择器 A B 4-to-1 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路分析 多路分配器的分析 D 译码器 A B 多 路 分 配 器 0 1 2 3 D A B Y0 Y1 Y2 Y3
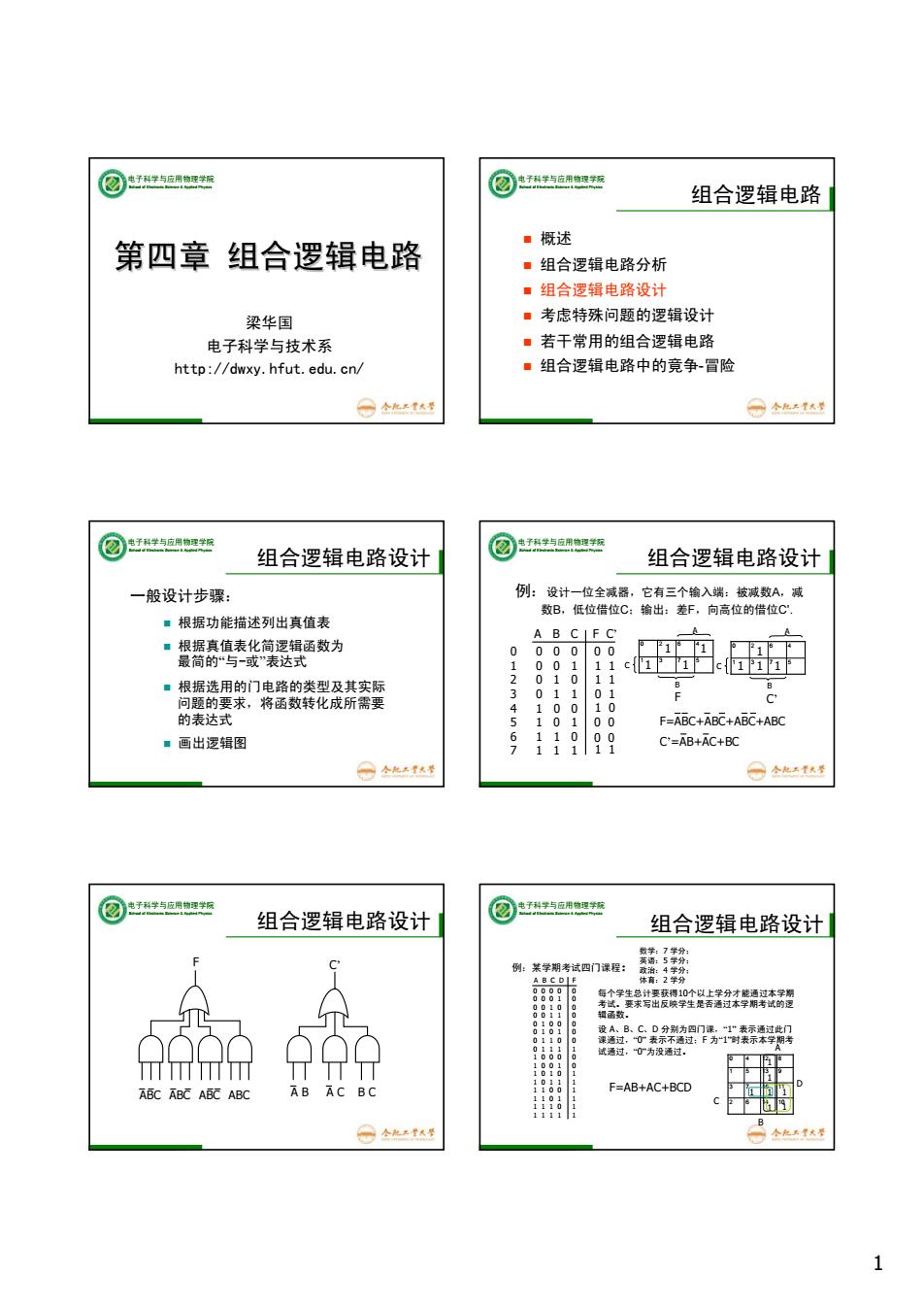
② 子科学与应用物理学标 电子科学与应用物理学标 组合逻辑电路 ·概述 第四章组合逻辑电路 ■组合逻辑电路分析 ■组合逻辑电路设计 梁华国 ·考虑特殊问题的逻辑设计 电子科学与技术系 ■若干常用的组合逻辑电路 http://dwxy.hfut.edu.cn/ ■组合逻辑电路中的竟争冒险 ⊙个北三生秋置 ⊙个北51热8 ② 电子科学与应用物理学纹 @ 电子科学与应用物理学粉 组合逻辑电路设计 组合逻辑电路设计 一般设计步骤: 例:设计一位全减器,它有三个输入端:被减数A,减 数B,低位借位C:输出:差F,向高位的借位C ■根据功能描述列出真值表 A B CIFC ■根据真值表化简逻辑函数为 0 00000 1F下1 15下 最简的“与一或”表达式 00111 ■根据选用的门电路的类型及其实际 010 1 c{1i☐1i1F B 0110 问题的要求,将函数转化成所需要 0 100 的表达式 101 0 F=ABC+ABC+ABC+ABC ■画出逻辑图 999 0 1 C'=AB+AC+BC ○个化天达 ⊙个儿去么行 ②于学与位用理想 电子科学与应用物理学酸 组合逻辑电路设计 ② 组合逻辑电路设计 封 例:某学期考试四门课程: 季纷 888 每个学生总计要获得10个以上学分才能通过本学阴 889 考试。要求写出反映学生是否通过本学期考试的逻 0000000100111111 辑函数。 889 设 B CD分别为四门课,“1”表示通过此门 课通过,表示不通过:F为“1时表示本学期考 试通过,“为没通过. ABC ABC ABCABC AB AC BC F=AB+AC+BCD ⊙个机2 1
1 电子科学与应用物理学院 School of Electronic Science & Applied Physics 梁华国 电子科学与技术系 http://dwxy.hfut.edu.cn/ 第四章 组合逻辑电路 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 考虑特殊问题的逻辑设计 若干常用的组合逻辑电路 组合逻辑电路中的竟争-冒险 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 一般设计步骤: 根据功能描述列出真值表 根据真值表化简逻辑函数为 最简的“与-或”表达式 根据选用的门电路的类型及其实际 问题的要求,将函数转化成所需要 的表达式 画出逻辑图 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 例:设计一位全减器,它有三个输入端:被减数A,减 数B,低位借位C;输出:差F,向高位的借位C’. 0 0 1 1 1 1 0 0 1 1 0 1 1 0 0 0 A B C F C’ 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 0 1 2 3 4 5 6 7 1 3 7 5 0 2 6 4 1 3 7 5 0 2 6 4 F C A B 1 1 1 1 A B C C’ 111 1 F=ABC+ABC+ABC+ABC C’=AB+AC+BC 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 F ABC ABC ABC ABC A B A C B C C’ 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 例:某学期考试四门课程: 数学:7 学分; 英语:5 学分; 政治:4 学分; 体育:2 学分 每个学生总计要获得10个以上学分才能通过本学期 考试。要求写出反映学生是否通过本学期考试的逻 辑函数。 设 A、B、C、D 分别为四门课,“1” 表示通过此门 课通过,“0” 表示不通过;F 为“1”时表示本学期考 试通过,“0”为没通过。 0 0 0 0 0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 0 0 1 1 0 0 0 1 1 1 1 1 0 0 0 0 1 0 0 1 0 1 0 1 0 1 1 0 1 1 1 1 1 0 0 1 1 1 0 1 1 1 1 1 0 1 1 1 1 1 1 A B C D F 2 6 14 10 3 7 15 11 1 5 13 9 0 4 12 8 A B C D 1 1 1 1 1 1 1 F=AB+AC+BCD

②好学与应用 电子科学与应用物理学板 组合逻辑电路设计 组合逻辑设计 例:已知X=xX2和Y=yy2是两个正整数, 逻辑函数的“与非”门实现 写出判断X>Y的逻辑表达式。 1.原函数二次反演,一次展开: X>Y的简化真值表 F=XiV+XX2V1Y2+xiX2YiV2 X1 X2 y1 y2 F 例如:F=AB+BC+CD+DA 1① 1×0x A 0100 3 回 F=AB+BC+CD+DA 1110 y @ 1111 11 AB-BC-CD-DA AB BC CD DA XiV1 XXV1V2 XiX2ViV2 F=x1+x22+xx22 B ⊙个北三生秋置 ⊙个北51热 ② 电子科学与应用物理学网 电子科学与应用物理学粉 组合逻辑电路设计 组合逻辑电路设计 逻辑函数的“或非"”门实现 2.反函数三次反演,一次展开: 采用“与非”门实现的对偶方法·直接采用反演定理 F=ABCD+ABCD 例如:用或非门实现函数F=AB+BC+CA ☐111 1111 F=ABCD+ABCD 111 F=(A+B+C)(A+B+C)=A+B+C+A+B+C 111 111 D 1111 =ABC5·ABCD 111 D TTTT mm 11☐1 -F ABCD ABCD B ○公化天达 F=ABC+ABC ⊙个也二1法行 电子科学与应用物理学院 组合逻辑电路设计 ②子学与应用理 习题 逻辑函数的“与或非”门实现 例如:用与或非门实现函数F=AB+BC+CA 对F两次求反F=AB+BC+C P61题2.12、2.13 对F-次求反F=AB+BC+C丽 P210-211题4.5、4.6、4.9 =ABC+ABC F=F-ABC+ABC ⊙个三A8 ⊙个人香 2
2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 例:已知 X=x1x2 和 Y=y1y2 是两个正整数, 写出判断 X>Y 的逻辑表达式。 1 1 1 0 x 0 0 1 0 1 x 0 1 1 1 x1 x2 y1 y2 F x1y1 x1x2y1y2 x1x2y1y2 F= x1y1+ x1x2y1y2+x1x2y1y2 1 1 1 1 1 1 x1 y1 y2 x2 F= x1y1 + x1x2y + x2 2 y1y2 X>Y 的简化真值表 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑设计 逻辑函数的“与非”门实现 1. 原函数二次反演,一次展开: 例如:F=AB+BC+CD+DA A B C D 1 1 1 1 1 1 1 1 1 1 1 1 1 1 F=AB+BC+CD+DA = AB•BC•CD•DA AB BC CD DA F 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 2. 反函数三次反演,一次展开: A B C D 1 1 1 1 1 1 1 1 1 1 1 1 1 1 F=ABCD+ABCD F=ABCD+ABCD =ABCD•ABCD ABCD A B C D F 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 逻辑函数的“或非”门实现 例如:用或非门实现函数 F=AB+BC+CA F= (A+B+C)•(A+B+C) A B C A B C F 采用“与非”门实现的对偶方法 直接采用反演定理 A B C D 1 1 1 1 1 1 1 1 1 1 1 1 F= ABC+ABC = A+B+C+A+B+C 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路设计 逻辑函数的“与或非”门实现 例如:用与或非门实现函数 F=AB+BC+CA 对F两次求反 F=AB+BC+CA 对F一次求反 F=AB+BC+CA =ABC+ABC F=F= ABC+ABC 电子科学与应用物理学院 School of Electronic Science & Applied Physics 习 题 P61 题2.12、2.13 P210-211题4.5、4.6、4.9

②子学与应用腰粉 组合逻辑电路 ② 电子科学与应用物理学 考虑特殊问题的逻辑设计 ·概述 ·多输出函数的逻辑设计 ·组合逻辑电路分析 例如:F1=AB+CD ■组合逻辑电路设计 F2=CD+CD ·考虑特殊问题的逻辑设计 公共的项并不总是很明显: ■若干常用的组合逻辑电路 F,=ABD+ACD ■组合逻辑电路中的竟争-冒险 F2=ABC+ACD+BCD 瓦而同 等效的F2=ACD+BCD+ABC c 8 ⊙个北三生秋置 3
3 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 考虑特殊问题的逻辑设计 若干常用的组合逻辑电路 组合逻辑电路中的竟争-冒险 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 多输出函数的逻辑设计 例如: F1=AB+CD F2=CD+CD C D A B C D F1 F2 • 公共的项并不总是很明显: 1 1 1 1 1 1 F1=ABD+ACD F2=ABC+ACD+BCD 等效的 F2=ACD+BCD+ABC A B C D F2

②子学与应用腰新 电子科学与应用物理学 组合逻辑电路 ② 考虑特殊问题的逻辑设计 ·概述 ·多输出函数的逻辑设计 ·组合逻辑电路分析 例如:F1=AB+CD ■组合逻辑电路设计 F2=CD+CD ·考虑特殊问题的逻辑设计 公共的项并不总是很明显: ■若干常用的组合逻辑电路 F,=ABD+ACD ■组合逻辑电路中的竟争-冒险 F2=ABC+ACD+BCD 佩而间 等效的F2=ACD+BCD+ABC c同 ⊙个北三生秋誉 ② 电子科学与应用物理学 电子科学与应用物理学 考虑特殊问题的逻辑设计 考虑特殊问题的逻辑设计 多输出的逻辑函数的化简步骤: 1.构成各自函数以及各个函数之间所有组合相 f3=m(1,6,7,8,9,10,11) 交的卡诺图。 求其一组最简的F「2,「"与或"表达式 F,=ABCD+BCD+AB 2.找出每个卡诺图的所有极大块,如果在高一 级以上相交卡诺图已圈过的极大块,在后继 F2=ABCD+ABCD+ACD 卡诺图中,不再圈出。 F:=ABCD+ABC+AB 3.构成函数的最小覆盖。对函数有关的所有卡诺 3 图,从高到低优先选择极大块,如果发现某级 的极大块被其它级极大块包含,此块应删去。 特点:点面相结合 ⊙个化天么学 F·F3 F2f3 公也天下长下 ②电子学与应用的 考虑特殊问题的逻辑设计 ② 电子科学与应用物理学 考虑特殊问题的逻辑设计 包含无关最小项的逻辑设计 在2个最小项中,一部分最小项并不能决定函数 的值,我们把这些最小项称为无关最小项 无关最小项发生在两种情况: ·输入某些组合不可能出现 。所有输入都可能出现,但其中部分输入对其 输出并不关心 A B BCD ABCD ACD ABC面ABC 化简依据:逻辑函数加上或者去掉无关最小项, 对原函数逻辑功能无影响 ⊙个工A号 y
1 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 考虑特殊问题的逻辑设计 若干常用的组合逻辑电路 组合逻辑电路中的竟争-冒险 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 多输出函数的逻辑设计 例如: F1=AB+CD F2=CD+CD C D A B C D F1 F2 • 公共的项并不总是很明显: 1 1 1 1 1 1 F1=ABD+ACD F2=ABC+ACD+BCD 等效的 F2=ACD+BCD+ABC A B C D F2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 多输出的逻辑函数的化简步骤: 1. 构成各自函数以及各个函数之间所有组合相 交的卡诺图。 2. 找出每个卡诺图的所有极大块,如果在高一 级以上相交卡诺图已圈过的极大块,在后继 卡诺图中,不再圈出。 3. 构成函数的最小覆盖。对函数有关的所有卡诺 图,从高到低优先选择极大块,如果发现某级 的极大块被其它级极大块包含,此块应删去。 特点:点面相结合 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 例如:已知有四个输入变量的三个逻辑函数: F1=m(5,7,8,9,10,11,13) F2=m(1,7,11,15) F3=m(1,6,7,8,9,10,11) 求其一组最简的F1,F2,F3”与-或”表达式。 2 6 14 10 3 7 15 11 1 5 13 9 0 4 12 8 1 1 1 1 1 1 1 F1 1 1 1 1 F2 1 1 1 1 1 1 1 F3 1 1 F1• F2 1 1 1 1 1 F1• F3 1 1 1 F2• F3 1 1 F1• F2• F3 F1=ABCD+BCD+AB F2= ABCD+ ABCD+ACD F3= ABCD+ ABC+AB A C B D 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 F1 A B BCD ABCD ACD • • • F2 F3 ABCD ABC 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 包含无关最小项的逻辑设计 在2n个最小项中,一部分最小项并不能决定函数 的值,我们把这些最小项称为无关最小项 无关最小项发生在两种情况: 输入某些组合不可能出现 所有输入都可能出现,但其中部分输入对其 输出并不关心 化简依据:逻辑函数加上或者去掉无关最小项, 对原函数逻辑功能无影响

② 电子科学与应用物理 考虑特殊问题的逻辑设计 ② 电子科学与应用物理 考虑特殊问题的逻辑设计 例如:用与非门设计一个判别电路,以判别8421码所 考虑级数的逻辑设计 表示的十进制数之值是否大于等于5 ABcD1E设:8421码对应输入变量:A,B,C,D,输出函数为F, 例:用与非门、与或非门分别实现以下函数 00000 ABCD≥0101时,F=1;当ABCD<0101时,F=0 F=AB+AC F=∑m(5,6,7,8,9)+∑p(10,11,12,13,14,15) Σp(10,11,12,13,14,15)=0 D F=BD+BC+A=BD-BC.A 下 DD 11 100 c中a D BP ⊙个北五秋誉 to F ⊙个人等 ② 电子科学与应用物理学网 课堂练习 1. 用代数法化简函数 F-AB+AC+CD+BCD+BCE+BCG+BCF 2. 已知逻辑函数:仁ABE+BCDE+BCDE+BCDE 的最简表达式为: F=BE+BDC 求其可确认的无关最小项。 3.分析右图, 并说明其逻辑功能 4. 设计一个二位二进制乘法器的 逻辑电路 A B 个机天 2
2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 例如:用与非门设计一个判别电路,以判别8421码所 表示的十进制数之值是否大于等于5 设:8421码对应输入变量:A,B,C,D, 输出函数为F, 0 0 0 0 0 ABCD 0101 时,F=1; 当ABCD 0101 时,F=0 0 0 0 1 0 0 0 1 0 0 0 0 1 1 0 0 1 0 0 0 0 1 0 1 1 0 1 1 0 1 0 1 1 1 1 1 0 0 0 1 1 0 0 1 1 A B C D F 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 F=m(5,6,7,8,9) (10,11,12,13,14,15)=0 +(10,11,12,13,14,15) 2 6 14 10 3 7 15 11 1 5 13 9 0 4 12 8 A B D C 1 1 1 1 1 F=BD+BC+A= BD•BC•A B D B C A F 电子科学与应用物理学院 School of Electronic Science & Applied Physics 考虑特殊问题的逻辑设计 考虑级数的逻辑设计 例:用与非门、与或非门分别实现以下函数: F=AB+AC 电子科学与应用物理学院 School of Electronic Science & Applied Physics 课堂练习 1. 用代数法化简函数 F=AB+AC+CD+BCD+BCE+BCG+BCF 2. 已知逻辑函数:F=ABE+BCDE +BCDE+BCDE 的最简表达式为:F=BE+BDC 求其可确认的无关最小项。 3. 分析右图,并说明其逻辑功能 4. 设计一个二位二进制乘法器的 逻辑电路 • • • • A B F1 F2 F3

电子科学与应用物理学院 第四章组合逻辑电路 梁华国黄正峰 电子科学与技术系 http://dwxy.hfut.edu.cn/ 合胞三堂大举 电子科学与应用物理学院 组合逻辑电路 概述 ■组合逻辑电路分析 ·组合逻辑电路设计 ·考虑特殊问题的逻辑设计 ■若干常用的组合逻辑电路 ·组合逻辑电路中的竟争-冒险 合他三营大坚 1
1 1 电子科学与应用物理学院 School of Electronic Science & Applied Physics 梁华国 黄正峰 电子科学与技术系 http://dwxy.hfut.edu.cn/ 第四章 组合逻辑电路 2 电子科学与应用物理学院 School of Electronic Science & Applied Physics 组合逻辑电路 概述 组合逻辑电路分析 组合逻辑电路设计 考虑特殊问题的逻辑设计 若干常用的组合逻辑电路 组合逻辑电路中的竟争‐冒险

电子科学与应用物理学院 4.3若干常用的组合逻辑电路 4.3.1编码器(Encoder) 编码:为了区分一系列不同的事物,将其中的每个事 物用二值代码表示。 编码器:由于在二值逻辑电路中,信号是以高低电 平给出的,故编码器就是把输入的每一个高低电平 信号变成一个对应的二进制代码。 编码器分为普通编码器和优先权编码器。根据进制 可分为二进制编码器和二土进制编码器。 个危三堂大举 电子科学与应用物理学院 4.3.1编码器 一、 普通编码器 3位二进制普通编码器,也称为8线-3线编码器,其 框图如图4.3.1所示 I0I,为信号输入端,高 线 电平有效:Y2Y1Yo为三 Y 位二进制代码输出端, 线编码 由于输入端为8个,输出 端为3个,故也叫做8线 图4.31位二进制编码器的框图 3线编码器 个他2誉大坚 2
2 3 电子科学与应用物理学院 School of Electronic Science & Applied Physics 4.3 若干常用的组合逻辑电路 4.3.1 编码器(Encoder) (Encoder) 编码:为了区分一系列不同的事物,将其中的每个事 物用二值代码表示。 编码器:由于在二值逻辑电路中,信号是以高低电 平给出的,故编码器就是把输入的每一个高低电平 信号变成一个对应的二进制代码。 编码器分为普通编码器和优先权编码器。根据进制 可分为二进制编码器和二‐十进制编码器。 4 电子科学与应用物理学院 School of Electronic Science & Applied Physics 4.3.1 编码器 I0~I7为信号输入端,高 电平有效;Y2Y1Y0为三 位二进制代码输出端, 由于输入端为8个,输出 端为3个,故也叫做8线- 3线编码器 一、 普通编码器 3位二进制普通编码器,也称为8线-3线编码器,其 框图如图4.3.1所示

② 电子科学与应用物理学院 4.3.1编码器 其输入、输出的真值表为 输 入 输出 利用无关项化简得到 0 0000 0 000 其输出端逻辑式为 000 001 00000 010 y2=14+15+16+17 0000 011 0 0 0 y=12+13+16+I7 0 00 110 Y%=1+13+15+7 00000001 111 特点:任何时刻只允许输入一个编码信号 5 合危子营大零 电子科学与应用物理学院 4.3.1编码器 其逻辑电路如图4.3.2所示 图4.3.23位二进制编码器(8线-3线编码器) 合他2营大坚 3
3 5 电子科学与应用物理学院 School of Electronic Science & Applied Physics 4.3.1 编码器 其输入、输出的真值表为 利用无关项化简得到 其输出端逻辑式为 特点:任何时刻只允许输入一个编码信号 6 电子科学与应用物理学院 School of Electronic Science & Applied Physics 4.3.1 编码器 其逻辑电路如图4.3.2所示 图4.3.2 3位二进制编码器(8线-3线编码器)