
第一章 逻辑代数基础 第一章逻辑代数与DA技 术的基础知识
第一章 逻辑代数与EDA技 术的基础知识

第一章 逻辑代数基础 本章需掌握的主要内容 ·L.二进制表示法、二进制与十进制之间的转 换 ·2.基本和常用的逻辑运算 ·3.當用逻辑公式 ·4.逻辑函数的化简 公式法和图形法 ·5.逻辑函数的表示方法
本章需掌握的主要内容 • 1.二进制表示法、二进制与十进制之间的转 换 • 2.基本和常用的逻辑运算 • 3.常用逻辑公式 • 4.逻辑函数的化简——公式法和图形法 • 5.逻辑函数的表示方法

第一章 逻辑代数基础 概述 一、逻辑代数(布尔代数、开关代数) 逻辑关系:事物间的因果关系。 逻辑代数:反映和处理逻辑关系的数学工具。 在二值逻辑中,逻辑变量取值只有两种:0、1, 分别代表两种对立的状态 种状态 高电平真是有 另一状态 低电平假非无 有三 0
另一状态 一种状态 一、逻辑代数(布尔代数、开关代数) 逻辑关系:事物间的因果关系。 逻辑代数: 反映和处理逻辑关系的数学工具。 在二值逻辑中,逻辑变量取值只有两种:0、1 , 分别代表两种对立的状态 高电平 低电平 真 假 是 非 有 无 … … 1 0 概 述

第一章 逻辑代数基础 二、二进制数表示法 1.十进制 (Decima)-逢十进 基数:10 位权:10 (143.75)0=1×102+4x10+3x10°+7×10H+5×102 2.二进制(Binary)-逢二进= 基数:2 位权:2 101.11)2=1×22+0×2+1×20+1×2+1×22
二、二进制数表示法 1. 十进制(Decimal)-- 逢十进一 基数:10 位权: 2. 二进制(Binary) -- 逢二进一 基数:2 位权: i 10i 2 2 1 0 1 2 1 10 4 10 3 10 7 10 5 10 − − ( 143.75 ) 10= + + + + 2 ( 101. 11 ) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + +

第一章 逻辑代数基础 3.八进制(Oca-逢八进 基数:8 位权:8 37.4103=3×8+7×80+4×8+1×8-2 4.十六进制(Hexadecima-逢十六进 基数:16 :0~9,A10,B(0,C(2,D3),E40,5 位权:16 (2A.7F)6=2×16+10×160+7×16+15×162 任意(W进制数展开式的普遍形式: D=∑kN k,一第i位的数码 一第位的权
3. 八进制(Octal)-- 逢八进一 基数:8 位权: 8 ( 37. 41 ) 1 0 1 2 3 8 7 8 4 8 1 8 − − = + + + 4. 十六进制 (Hexadecimal) --逢十六进一 基数:16 :0 ~ 9 , A(10) , B(11) , C(12) , D(13) , E(14) , F(15) 位权: i 8 i 16 16 ( 2A. 7F ) 1 0 1 2 2 16 10 16 7 16 15 16 − − = + + + 任意(N)进制数展开式的普遍形式: i D = ki N ki i — 第 i 位的数码 N — 第 i 位的权

第一章 逻辑代数基础 5.几种常用进制数之间的转换 )二十转换:将二进制数按位权展开后相加 (101.1102=1×22+0×2+1×20+1×2+1×22 =4+1+0.5+0.25=(⑤.75)0 2十二转换: 2 26 余数 2 13 0 整数的转换-除2取余法 降幂比较法 3 0 逆序排列 26)0=(110102
5. 几种常用进制数之间的转换 (1) 二-十转换: 将二进制数按位权展开后相加 2 ( 101.11 ) 2 1 0 1 2 1 2 0 2 1 2 1 2 1 2 − − = + + + + 10 = 4 + 1+ 0. 5 + 0. 25 = (5. 75) (2) 十-二转换: 整数的转换--除2取余法 降幂比较法 10 2 ( 26 ) = ( ) 2 26 13 余数 2 0 2 6 1 2 3 0 2 1 1 0 1 11010 逆 序 排 列
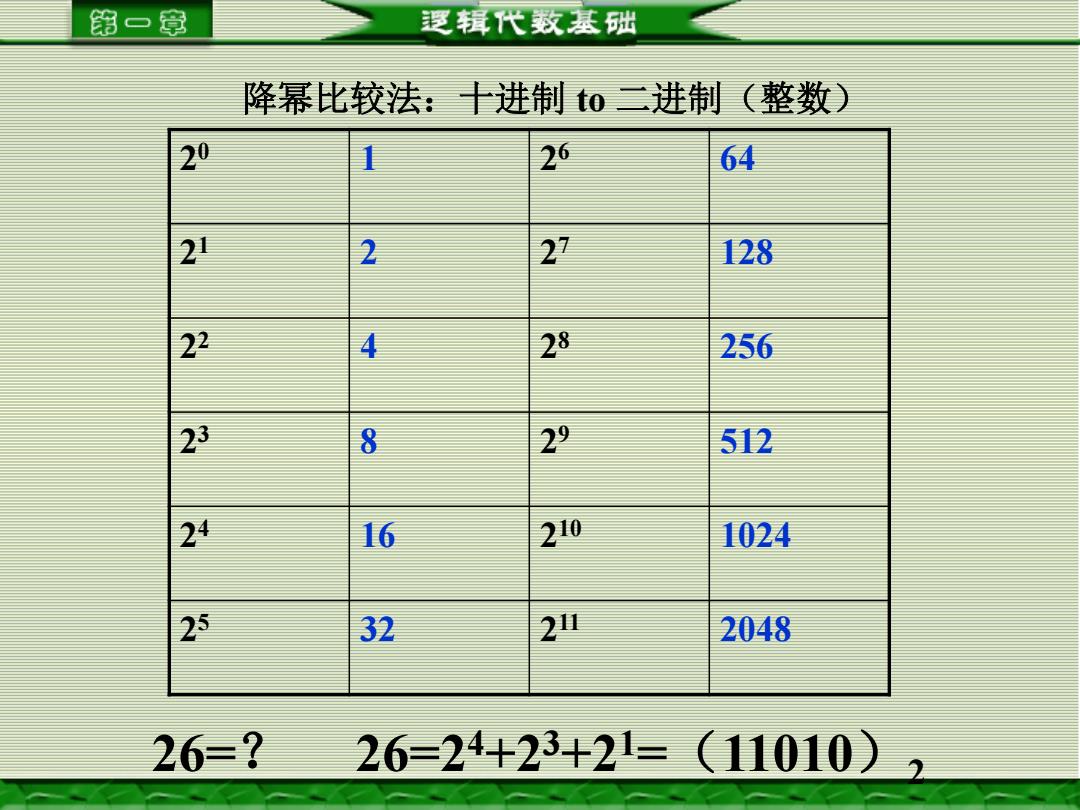
第一章 逻辑代数基础 降幂比较法:十进制二进制(整数) 20 26 64 21 2 27 128 22 4 28 256 23 8 29 512 24 16 20 1024 25 32 21 2048 26=? 26=24+23+2=(11010))
2 0 1 2 6 64 2 1 2 2 7 128 2 2 4 2 8 256 2 3 8 2 9 512 2 4 16 2 10 1024 2 5 32 2 11 2048 降幂比较法:十进制 to 二进制(整数) 26=? 26=24+23+21=(11010)2
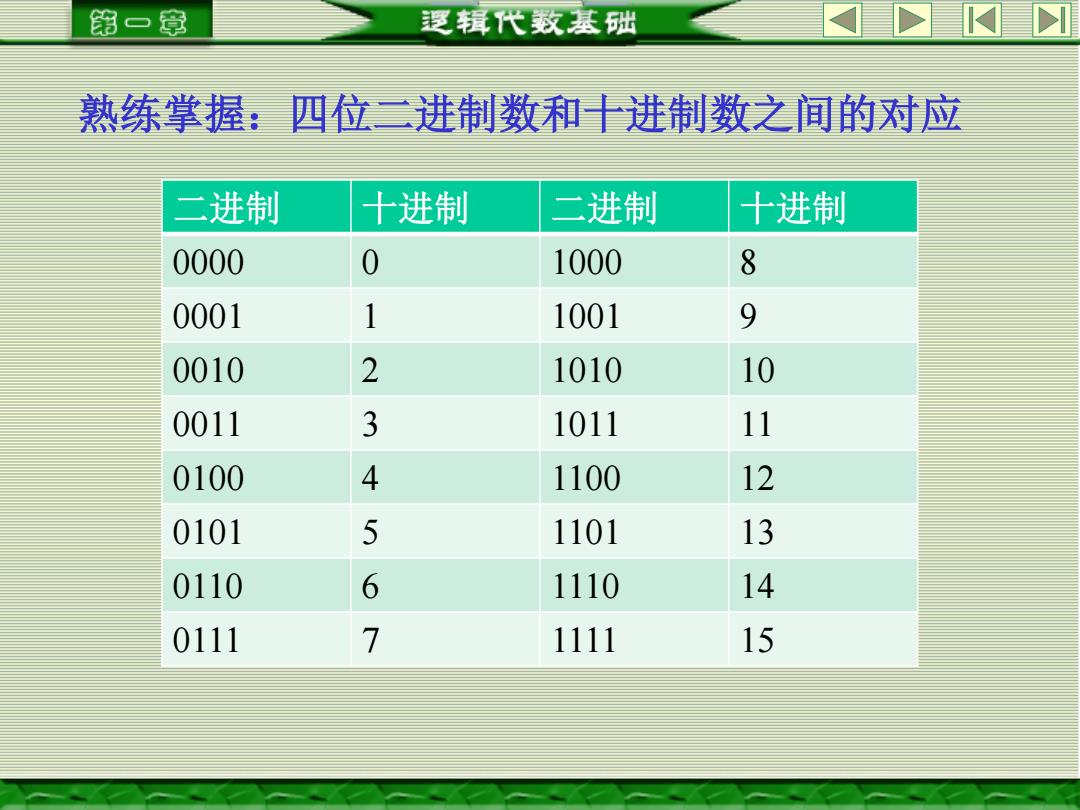
第一章 逻辑代数基础 熟练掌握:四位二进制数和十进制数之间的对应 二进制 十进制 二进制 十进制 0000 0 1000 8 0001 1 1001 9 0010 2 1010 10 0011 3 1011 11 0100 4 1100 12 0101 5 1101 13 0110 6 1110 14 0111 7 1111 15
熟练掌握:四位二进制数和十进制数之间的对应 二进制 十进制 二进制 十进制 0000 0 1000 8 0001 1 1001 9 0010 2 1010 10 0011 3 1011 11 0100 4 1100 12 0101 5 1101 13 0110 6 1110 14 0111 7 1111 15
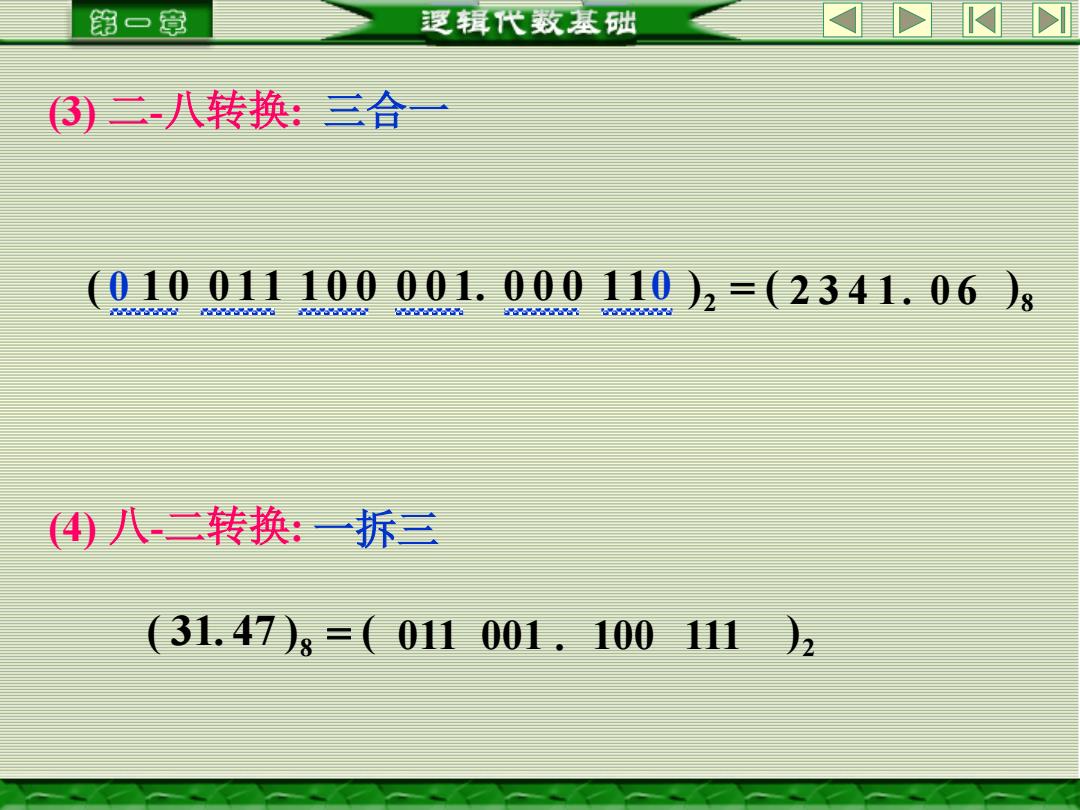
第一章 逻辑代数基础 3二-八转换:三合 010011100001.000110月2=(2341.06)8 32R3B383333333333283222R32333338323 4八二转换:一拆三 31.47)、=011001.100111)2
(3) 二-八转换: (4) 八-二转换: 一拆三 8 2 ( 31. 47 ) = ( 011 001 . 100 111 ) 三合一 2 8 ( 0 1 0 0 11 1 0 0 0 0 1. 0 0 0 11 0 ) = ( 2 3 4 1 . 0 6 )

第一章 逻辑代数基础 (5)二十六转换:四合一 00011011010.0010)2=(1B6.26 99aaa“ (6)十六二转换:拆四 (8FA.C6)6=(100011111010.11000110)2
(5)二-十六转换:四合一 (6)十六-二转换:一拆四 16 2 ( 8 F A .C 6 ) = ( 1 0 0 0 111 1 1 0 1 0 .1 10 0 0110 ) ( 1 1 0 11 0 11 0 . 0 0 1 ) ( ) 000 0 2 = 1B 6 . 2 16