
中国绅我术大空 University of Science and Technology of China 第一章数制和码制 本章目录 >1.1概述 >1.2几种常用的数制 >1.3不同数制间的转换 >1.4二进制算术运算 >1.5几种常用的编码 2017-8-4 第一章数制和码制 §1.1概述 一、数制 定义:多位数码中每一位的构成方法和从低位到高位的进位规则。 二、码制 定义:编制代码时所遵循的规则。 1编码 用文字、符号或者数字表示特定对象的过程。 2代码 具有特定含义的数码,用来表示不同的事物或事物的不同状态。 注:二进制代码的位数(),与需要编码的事物的个数N之间 应满足以下关系: 2"≥N 2017-8-4 第一章数制和码制
2017-8-4 第一章 数制和码制 1 第一章 数制和码制 第一章 数制和码制 本章目录 ¾1.1 概述 ¾1.2 几种常用的数制 ¾1.3 不同数制间的转换 ¾1.4 二进制算术运算 ¾1.5 几种常用的编码 2017-8-4 第一章 数制和码制 2 §1.1 概述 一、数制 定义:多位数码中每一位的构成方法和从低位到高位的进位规则。 2 代码 具有特定含义的数码,用来表示不同的事物或事物的不同状态。 二、码制 定义:编制代码时所遵循的规则。 注:二进制代码的位数(n),与需要编码的事物的个数(N)之间 应满足以下关系: 2n ≥ N 1 编码 用文字、符号或者数字表示特定对象的过程

§1.2几种常用的数制 © ●常用的数制 十进制,二进制,十六进制,八进制 ●数的表示方法 位置记数法、多项式法 2017-8-4 第一章数制和码制 §1.2几种常用的数制 一、十进制 每一位的构成:0,1,2,3,4,5,6,7,8,9 进位规则:逢十进一 任意一个n位整数、m位小数的十进制数可表示为 (D)1o=kn-kn-2…kk1…km =kn-1×10m-+…+k×10°+k1×10-1+…+km×10-m -0 i=-m 推广:任意进制(N进制)数可表示为:(D)w=∑k,N k:第位的系数;N:计数的基数;N:第位的权 2017-8-4 第一章数制和码制
2017-8-4 第一章 数制和码制 3 §1.2 几种常用的数制 z常用的数制 十进制,二进制,十六进制,八进制 z数的表示方法 位置记数法、多项式法 2017-8-4 第一章 数制和码制 4 §1.2 几种常用的数制 一、十进制 每一位的构成:0,1,2,3,4,5,6,7,8,9 进位规则:逢十进一 任意一个n位整数、m位小数的十进制数可表示为 i n i m i m m n n n n m k k k k k D k k k k k 10 10 10 10 10 ( ) . 1 1 1 0 0 1 1 10 1 2 0 1 = × = × + + × + × + + × = ∑ − =− − − − − − − − − − − L L L L k:第i位的系数;N:计数的基数;N :第i位的权 i i 推广:任意进制(N进制)数可表示为: i (D)N = ∑kiN
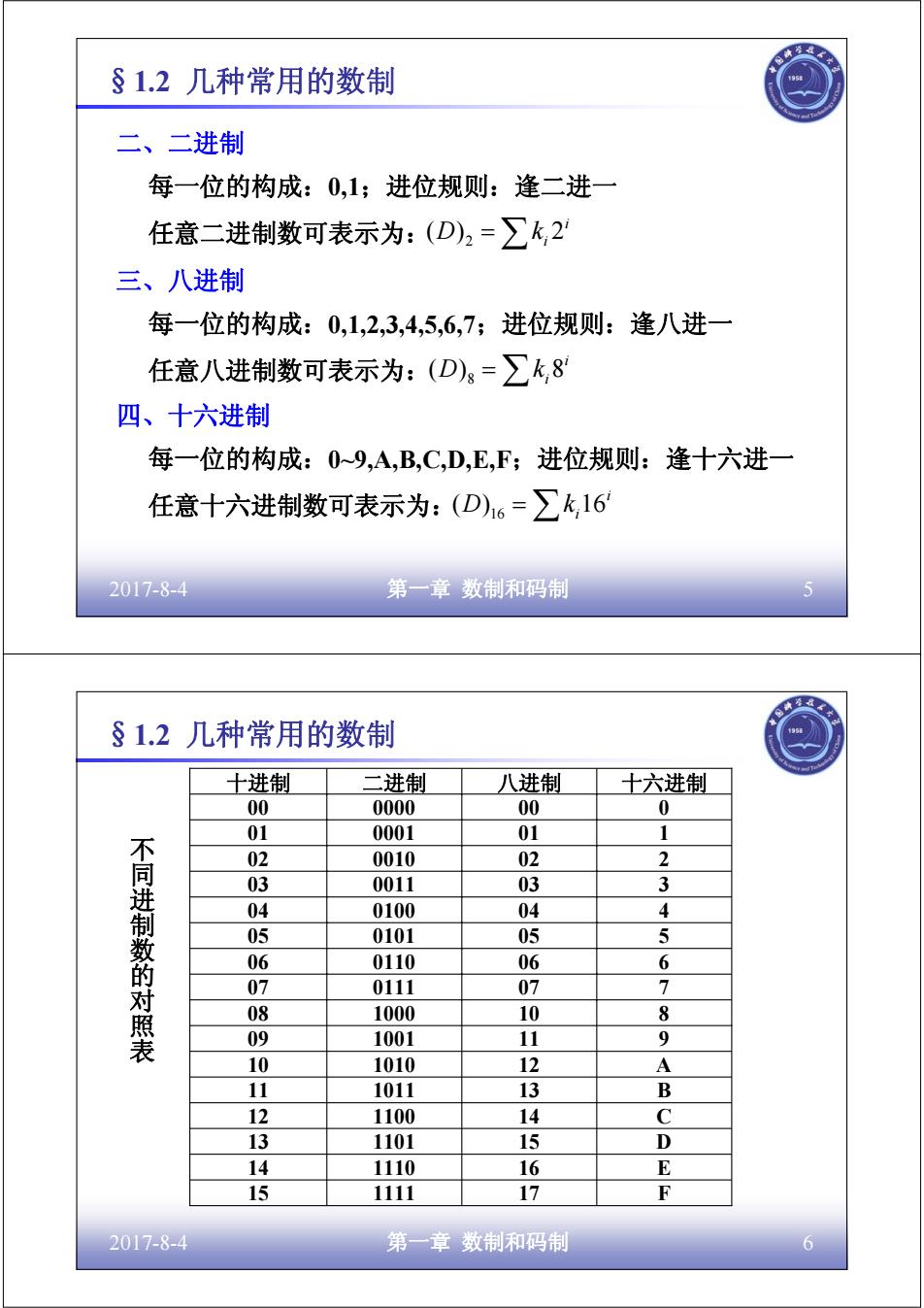
§1.2几种常用的数制 二、二进制 每一位的构成:0,1;进位规则:逢二进一 任意二进制数可表示为:(D)2=∑k,2 三、八进制 每一位的构成:0,1,2,3,4,5,6,7;进位规则:逢八进一 任意八进制数可表示为:(D)g=∑k,8 四、十六进制 每一位的构成:0~9,A,B,C,D,E,F;进位规则:逢十六进一 任意十六进制数可表示为:(D)16=∑k,16 2017-8-4 第一章数制和码制 5 §1.2几种常用的数制 十进制 二进制 八进制 十六进制 00 0000 00 0 01 0001 01 1 02 0010 02 2 不同进制数的对照表 03 0011 03 3 04 0100 04 4 05 0101 05 5 06 0110 06 6 07 0111 07 7 08 1000 10 8 09 1001 11 9 10 1010 12 A 11 1011 13 B 12 1100 14 C 13 1101 15 D 14 1110 16 E 15 1111 17 F 2017-8-4 第一章数制和码制 6
2017-8-4 第一章 数制和码制 5 §1.2 几种常用的数制 二、二进制 每一位的构成:0,1;进位规则:逢二进一 任意二进制数可表示为: i i (D) k 2 2 = ∑ 三、八进制 每一位的构成:0,1,2,3,4,5,6,7;进位规则:逢八进一 任意八进制数可表示为: i i (D) k 8 8 = ∑ 四、十六进制 每一位的构成:0~9,A,B,C,D,E,F;进位规则:逢十六进一 任意十六进制数可表示为: i i (D) k 16 16 = ∑ 2017-8-4 第一章 数制和码制 6 14 1110 16 E 11 1011 13 B 10 1010 12 A 12 1100 14 C 09 1001 11 9 13 1101 15 D 15 1111 17 F 8 7 6 5 4 3 2 1 0 十六进制 00 0000 00 01 0001 01 03 0011 03 08 1000 10 02 0010 02 07 0111 07 06 0110 06 05 0101 05 04 0100 04 十进制 二进制 八进制 不同进制数的对照表 §1.2 几种常用的数制

§1.3不同数制间的转换 一、任意进制数转换为十进制数 利用公式:(D)N=∑k,N 例:将下面给出的二进制、八进制和十六进制数转换为等值的 十进制数。 (1011.01)2=1×23+0×22+1×2+1×2°+0×21+1×22 =(11.25)10 (32.56)g=3×8+2×8°+5×81+6×8-2 =(26.71875)10 (2A.7F)16=2×16+10×16°+7×16-1+15×16-2 =(42.49609375)10 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 二、十进制数转换为二进制数 一—基数乘除法 整数部分——基数除法 (S)1o=(kkn-1k-2kk)2 (S)0=k,2”+kn-2m+kn-22-2+k2+k20 =2(k2+kn12-2+…+k)+k。 kn2-+kn-12-2+…+k=2(kn2-2+kn-2"-3+…+k2)+k 2017-8-4 第一章数制和码制 8
2017-8-4 第一章 数制和码制 7 = ∑ i (D)N kiN §1.3 不同数制间的转换 2 (1011.01) 8 (32.56) 10 1 0 1 2 (42.49609375) 2 16 10 16 7 16 15 16 = = × + × + × + × − − 一、任意进制数转换为十进制数 例:将下面给出的二进制、八进制和十六进制数转换为等值的 十进制数。 10 3 2 1 0 1 2 (11.25) 1 2 0 2 1 2 1 2 0 2 1 2 = = × + × + × + × + × + × − − 10 1 0 1 2 (26.71875) 3 8 2 8 5 8 6 8 = = × + × + × + × − − 16 (2A.7F) 利用公式: 2017-8-4 第一章 数制和码制 8 0 0 1 1 2 2 1 (S)10 k 2 k 1 2 k 2 k 2 k 2 n n n n n = n + + + + − − − − L 二、十进制数转换为二进制数 2 1 3 1 2 1 2 1 1 k 2 k 2 k 2(k 2 k 2 k ) k n n n n n n n n + + + = + + + + − − − − − − L L ——基数乘除法 整数部分——基数除法 1 0 2 1 1 2(k 2 k 2 k ) k n n n = n + + + + − − − L §1.3 不同数制间的转换 10 1 2 1 0 2 (S) (k k k k k ) = n n− n− L LL

§1.3不同数制间的转换 © 例:(173)10=( )2 2173…余数1(k) 286... 余数0(k) 243 ··。· 余数1(k2) 221…余数1(k) 210 ·…·余数0(k4) 2 5 余数1(k) 2 2 …·余数0(k6) 1 余数1(k) 0 .(173)10=(10101101)2 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 二、十进制数转换为二进制数 ——基数乘除法 小数部分——基数乘法 (S)10=(0.kk2…km)2 (S)10=k121+k222+…+km2m 2(S)h0=k1+(k221+k32-2+…+km2-m+1) 2(k22+k,2-2+…+km2m)=k2+(k32-++km2m+2) 2017-8-4 第一章数制和码制 10
2017-8-4 第一章 数制和码制 9 例: LL LLLLLLLLLLLLLL ( ) 0 k ( )1 k ( ) 2 k ( ) 3 k ( ) 4 k ( ) 5 k ( ) 6 k ( ) 7 k 余数 余数 余数 余数 余数 余数 余数 余数 10 2 (173) = ( ) 10 2 ∴(173) = (10101101) §1.3 不同数制间的转换 2017-8-4 第一章 数制和码制 10 二、十进制数转换为二进制数 ——基数乘除法 小数部分——基数乘法 m m S k k k − − − − − ( ) = − 2 + 2 + + 2 2 2 1 10 1 L 2( ) ( 2 2 2 ) 2 1 3 1 10 1 2 − + − − − − = − + − + + + m m S k k k L k 2( 2 2 2 ) ( 2 2 ) 1 2 2 3 2 1 3 1 2 − + − − − − − + − − − − − + + + = + + + m m m m k k L k k k L k §1.3 不同数制间的转换 10 1 2 2 ( ) (0. ) m S k k k = − − L − LL

§1.3不同数制间的转换 例:(0.8125)10=( )2 0.8125 × 2 …整数部分=1=k 1.6250 0.6250 ×2 …整数部分=1=k2 1.2500 0.2500 2 …整数部分=0=k 0.5000 0.5000 X 2 …整数部分=1=k4 1.0000 ∴.(0.8125)10=(0.1101)2 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 三、二进制数转换为十六进制和八进制数 例:将(1011110.1011001),转换成十六进制和八进制数。 解:(1011110.1011001)2=(01011110.10110010)2 =(5E.B2)16 (1011110.10110012=(001011110.101100100)2 =(136.544)8 四、八进制和十六进制数转换为二进制数 例:将(703.65)3和(9FC.4A)16转换成二进制数。 解:(703.65)3=(111000011.110101)2 (9FC.4A)16=(100111111100.01001010)2 2017-8-4 第一章数制和码制 12
2017-8-4 第一章 数制和码制 11 例: 10 2 (0.8125) = ( ) 10 2 ∴(0.8125) = (0.1101) 4 3 2 1 1 1.0000 2 0.5000 0 0.5000 2 0.2500 1 1.2500 2 0.6250 1 1.6250 2 0.8125 − − − − × × × × k k k k 整数部分= = 整数部分= = 整数部分= = 整数部分= = LL LL LL LL §1.3 不同数制间的转换 2017-8-4 第一章 数制和码制 12 三、二进制数转换为十六进制和八进制数 四、八进制和十六进制数转换为二进制数 (1011110.1011001) 2 =(001 011 110.101 100 100) 2 = (136.544) 8 (1011110.1011001) 2 = (0101 1110.1011 0010) 2 = (5E.B2)16 例:将(1011110.1011001) 2转换成十六进制和八进制数。 解: 例:将(703.65)8 和(9FC.4A)16 转换成二进制数。 (703.65)8 =(111 000 011.110 101)2 (9FC.4A)16 = (1001 1111 1100.0100 1010)2 解: §1.3 不同数制间的转换

§1.3不同数制间的转换 五、八进制数和十六进制数的互相转换 八进制数→二进制数→十六进制数 十六进制数→二进制数→八进制数 六、十进制数转换为八进制和十六进制数 十进制数→二进制数→八进制数 十进制数→二进制数→十六进制数 2017-8-4 第一章数制和码制 §1.3不同数制间的转换 例:对火星的首次探险发现的仅仅是文明的废墟。从石器和图 片中,探险家们推断创造这些文明的生物有四条腿,其触角末 端长着一些抓东西的“手指”。经过很多研究后,探险家们终于 能够翻译火星人的数学,他们发现了下面的等式: 5x2-50x+125=0 所指出的解为=5和=8。其中=5这个解看上去非常合理,但 是=8这个解就需要某种解释。于是,探险家们反思了地球的 计数体制发展,并且发现了火星的计数体制也有类似历史发展 的证据。你认为火星人有几个手指?(来自1956年2月的 《The Bent of Tau Beta Pi》)) 2017-8-4 第一章数制和码制 14
2017-8-4 第一章 数制和码制 13 五、八进制数和十六进制数的互相转换 六、十进制数转换为八进制和十六进制数 八进制数→二进制数→十六进制数 十六进制数→二进制数→八进制数 十进制数→二进制数→八进制数 十进制数→二进制数→十六进制数 §1.3 不同数制间的转换 2017-8-4 第一章 数制和码制 14 例:对火星的首次探险发现的仅仅是文明的废墟。从石器和图 片中,探险家们推断创造这些文明的生物有四条腿,其触角末 端长着一些抓东西的“手指”。经过很多研究后,探险家们终于 能够翻译火星人的数学,他们发现了下面的等式: 所指出的解为x=5和x=8。其中x=5这个解看上去非常合理,但 是x=8这个解就需要某种解释。于是,探险家们反思了地球的 计数体制发展,并且发现了火星的计数体制也有类似历史发展 的证据。你认为火星人有几个手指?(来自1956年2月的 《The Bent of Tau Beta Pi》) 5 50 125 0 2 x − x + = §1.3 不同数制间的转换

§1.4二进制算术运算 1.4.1二进制算术运算的特点 加法运算规则: 0+0=00+1=1 1+0=11+1=0(同时向相邻高位进1) 减法运算规则: 0-0=00-1=1(同时向相邻高位借1) 1-0=11-1=0 乘法运算规则: 0×0=0 0×1=0 1×0=0 1×1=1 除法运算规则: 0÷1=01÷1=1 2017-8-4 第一章数制和码制 §1.4二进制算术运算 例:两个二进制数1001和0101的算术运算(加、减、乘、除) 1001 1001 +0101 -0101 1110 0100 1.11 1001 01011001 ×0101 0101 1001 1000 0000 0101 1001 0110 0000 0101 0101101 0010 二进制算术运算的特点:加、减、乘、除运算全部可以用 “移位”和“相加这两种操作实现。简化了电路结构。 2017-8-4 第一章数制和码制 16
2017-8-4 第一章 数制和码制 15 1.4.1 二进制算术运算的特点 §1.4 二进制算术运算 加法运算规则: 减法运算规则: 乘法运算规则: 1 0 1 1 1 (同时向相邻高位进 0 1) 0 0 0 0 1 1 + = + = + = + = 1 0 1 1 1 0 0 0 0 0 1 1 1 − = − = − = − =(同时向相邻高位借 ) 1 0 0 1 1 1 0 0 0 0 1 0 × = × = × = × = 除法运算规则: 0 ÷1 = 0 1÷1 =1 2017-8-4 第一章 数制和码制 16 1 1 1 0 0 1 0 1 1 0 0 1 + 0 1 0 0 0 1 0 1 1 0 0 1 − 0 1 0 1 1 0 1 0 0 0 0 1 0 0 1 0 0 0 0 1 0 0 1 0 1 0 1 1 0 0 1 × 0 0 1 0 0 1 0 1 0 1 1 0 0 1 0 1 1 0 0 0 0 1 0 1 1. 1 1 0 1 0 1 1 0 0 1 ... 例:两个二进制数1001和0101的算术运算(加、减、乘、除) §1.4 二进制算术运算 二进制算术运算的特点:加、减、乘、除运算全部可以用 “移位”和“相加”这两种操作实现。简化了电路结构

§1.5几种常用的编码 一、十进制代码 用二进制代码来表示十进制数的0~9十个状态。 十进制数 8421码 余3码 2421码 5211码 余3循环码 0 0000 0011 0000 0000 0010 1 0001 0100 0001 0001 0110 2 0010 0101 0010 0100 0111 3 0011 0110 0011 0101 0101 4 0100 0111 0100 0111 0100 5 0101 1000 1011 1000 1100 6 0110 1001 1100 1001 1101 7 0111 1010 1101 1100 1111 8 1000 1011 1110 1101 1110 9 1001 1100 1111 1111 1010 权 8421 2421 5211 2017-8-4 第一章数制和码制 §1.5几种常用的编码 二、格雷码 编码顺序 二进制码 格雷码 编码顺序 二进制码 格雷码 0 0000 0000 8 1000 1100 1 0001 0001 9 1001 1101 2 0010 0011 10 1010 1111 3 0011 0010 11 1011 1110 4 0100 0110 12 1100 1010 5 0101 0111 13 1101 1011 6 0110 0101 14 1110 1001 0111 0100 15 1111 1000 特点:相邻两个代码之间只有一位不同。 优点:代码转换过程中不会产生过渡“噪声”。 2017-8-4 第一章数制和码制 18
2017-8-4 第一章 数制和码制 17 9 1001 1100 1111 1111 1010 权 8421 2421 5211 1110 1101 1100 1011 0100 0011 0010 0001 0000 2421码 1101 1100 1001 1000 0111 0101 0100 0001 0000 5211码 1110 1111 1101 1100 0100 0101 0111 0110 0010 余3循环码 0 0000 0011 1 0001 0100 3 0011 0110 8 1000 1011 2 0010 0101 7 0111 1010 6 0110 1001 5 0101 1000 4 0100 0111 十进制数 8421码 余3码 §1.5 几种常用的编码 一、十进制代码 用二进制代码来表示十进制数的0~9十个状态。 2017-8-4 第一章 数制和码制 18 15 14 13 12 11 10 9 8 编码顺序 1111 1110 1101 1100 1011 1010 1001 1000 二进制码 1000 1001 1011 1010 1110 1111 1101 1100 格雷码 0 0000 0000 1 0001 0001 3 0011 0010 2 0010 0011 7 0111 0100 6 0110 0101 5 0101 0111 4 0100 0110 编码顺序 二进制码 格雷码 二、格雷码 特点:相邻两个代码之间只有一位不同。 优点:代码转换过程中不会产生过渡“噪声”。 §1.5 几种常用的编码

§1.5几种常用的编码 三、美国信息交换标准代码(ASCI四 ASCIⅡ码是一组7位二进制代码,共128个。可以表示大、小写 英文字母、十进制数、标点符号、运算符号、控制符号等。 应用:计算机和通信领域 b:bab, 6,b,63b 000 001 010 011 100 101 110 111 0000 NUL DLE SP 0 例:写出以下ASCIⅡ码 0001 SOH DCI 9 R 表示的含义。 0010 STX DC2 2 0011 ETX DC3 3 0100 EOT DC4 4 D T 1010101 0101 ENQ NAK % 5 0110 ACK SYN & 6 F 011 EL ETB 7 G 1000110 100 H X 1001 HT 9 1010 e 1001111 1011 VT FF L 1101 M 1110 5s0 N 1111 SI US 0 DEL 2017-8-4 第一章数制和码制 19
2017-8-4 第一章 数制和码制 19 三、美国信息交换标准代码(ASCII) ASCII码是一组7位二进制代码,共128个。可以表示大、小写 个。 英文字母、十进制数、标点符号、运算符号、控制符号等。 应用:计算机和通信领域 例:写出以下ASCII码 表示的含义。 1010101 1000110 1001111 §1.5 几种常用的编码