
数字电子技术 第四章组合量} 4.2加法器 4.2.1二进制数的算术运算 一、两个绝对值之间的运算 运算规则,加法:“逢二进一”;减法:“借一当二”。 加、减、乘、除。 1001+0101=? 1001-0101=? 1011×0101=? 11001÷101=? 乘法运算可以通过连续的加法运算来实现;除 法运算可以通过连续的减法运算来实现。如 9X3,9÷3
第四章 组合逻辑电路 4.2 加法器 4.2.1 二进制数的算术运算 一、两个绝对值之间的运算 运算规则,加法:“逢二进一”;减法:“借一当二” 。 加、减、乘、除。 1001+0101=? 1001-0101=? 1011×0101=? 11001÷101=? 乘法运算可以通过连续的加法运算来实现;除 法运算可以通过连续的减法运算来实现。如 9×3,9÷3

数字电子技术 第四章组合量} 4.2加法器 4.2.1二进制数的算术运算 一、原码、反码和补码 (1)原码=符号--数值。(0?正1负) +1010101的原码?-1010101的原码? (2)反码表示 正数的反码=原码; 负数的反码=符号--数值按位取反。 +1010101的反码?-1010101的反码?
第四章 组合逻辑电路 4.2 加法器 4.2.1 二进制数的算术运算 一、原码、反码和补码 (1)原码=符号---数值。(‘0’正‘1’负) +1010101的原码?﹣1010101的原码? (2)反码表示 正数的反码=原码; 负数的反码=符号---数值按位取反。 +1010101的反码?﹣1010101的反码?

数字电子技术 第四章组合量}☒ 4.2加法器 4.2.1二进制数的算术运算 一、原码、反码和补码 (3)补码表示 正数的补码=原码: 负数的补码=反码+1。 +1010101的补码?-1010101的补码? -1的8位二进制原码、反码、补码?
第四章 组合逻辑电路 4.2 加法器 4.2.1 二进制数的算术运算 一、原码、反码和补码 (3)补码表示 正数的补码=原码; 负数的补码=反码+1。 +1010101的补码?﹣1010101的补码? -1的8位二进制原码、反码、补码?

数字电子技术 第四章组合量} 4.2加法器 4.2.1二进制数的算术运算 一、原码、反码和补码 补码运算规则:补码的补码是原码;两 数补码之和等于两数之和的补码。即 [补码]补码原码; [X1]补码+[X2]补码=[X1+X2]补码 减法运算电路结构复杂,运算速度慢;相对而 言,加法电路结构简单,运算速度快。故常将 减一个数变为加上一个负数,负数用补码表示 就可以将减法变为加法运算
第四章 组合逻辑电路 4.2 加法器 4.2.1 二进制数的算术运算 一、原码、反码和补码 补码运算规则:补码的补码是原码;两 数补码之和等于两数之和的补码。即 减法运算电路结构复杂,运算速度慢;相对而 言,加法电路结构简单,运算速度快。故常将 减一个数变为加上一个负数,负数用补码表示 就可以将减法变为加法运算。 [补码]补码=原码; [X1]补码+[X2]补码=[X1+X2]补码

数字电子技述 第四章组合量 4.2加法器 4.2.1二进制数的算术运算 用补码运算:1101-1010=?0110-1001=? 注意:在进行补码运算时,必须在其相应位数 表示的数值范围内进行,否则会产生错误的运 算结果。 综上所述,二进制数的加、减、乘、除运 算都可以通过加法运算来实现 实现加法运算的器件称为加法器,它是计 算机重要的组成单元
第四章 组合逻辑电路 4.2 加法器 4.2.1 二进制数的算术运算 用补码运算: 1101-1010=?0110-1001=? 综上所述,二进制数的加、减、乘、除运 算都可以通过加法运算来实现。 实现加法运算的器件称为加法器,它是计 算机重要的组成单元

数字电子技术 第四章组合 4.2加法器和数值比较器 4.2.2 加法器 一、半加器和全加器 1.半加器(Half Adder) 两个1位二进制数相加。 A+B;=S:(和)→C:(进位) A:Bi S; C 函数式 真值表 0 S=A;Bi+A;Bi 0 1 1 1 0 =A⊕B 1 0 Ci=AiBi
第四章 组合逻辑电路 4.2 加法器和数值比较器 4.2.2 加法器 一、半加器和全加器 1. 半加器(Half Adder) 两个 1 位二进制数相加。 0 0 0 1 1 0 1 1 0 0 1 0 1 0 0 1 真 值 表 函数式 Ai+Bi = Si (和) Ci (进位)
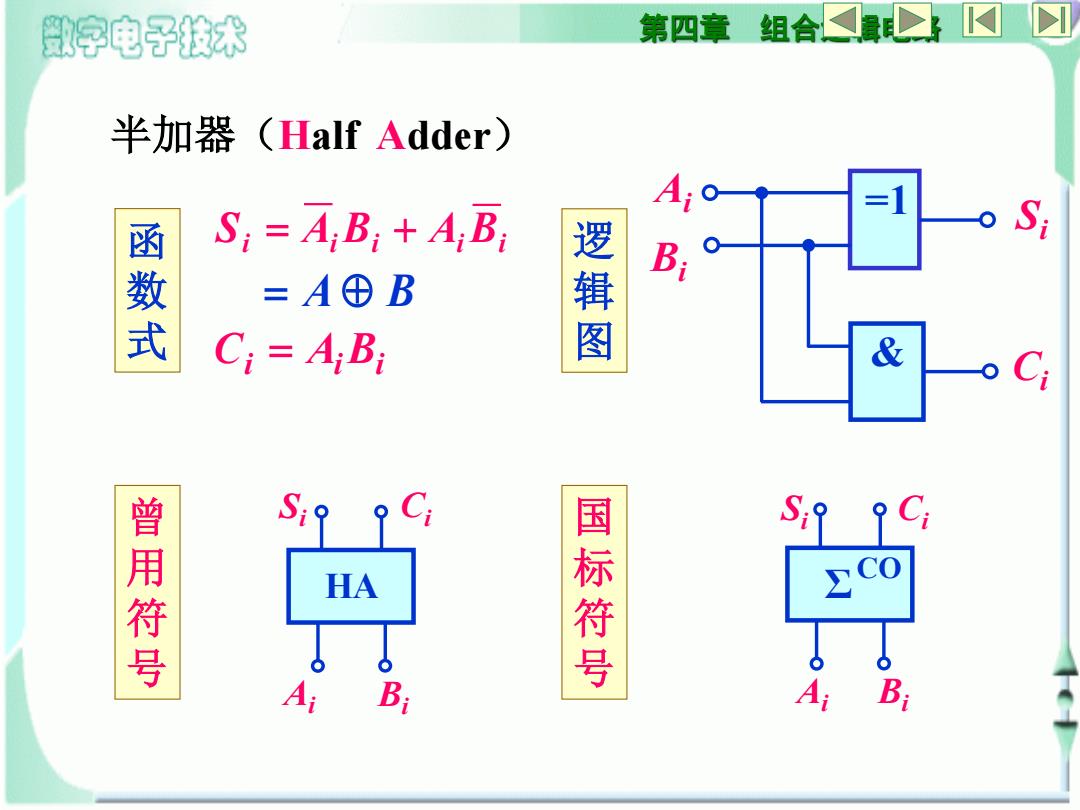
数字电子技术 第四章 组合量 半加器 (Half Adder) Si=A B+AB 函数式 逻辑图 Bi =A⊕B Ci=AiBi & S 曾用符号 HA 国标符号 Bi A B
第四章 组合逻辑电路 逻 辑 图 曾 用 符 号 国 标 符 号 半加器(Half Adder) Si & Ai Bi =1 Ci Σ CO Si Ai Bi Ci HA Si Ai Bi Ci Si Ai Bi Ai Bi Ci Ai Bi 函 数 式 A B

数字电子技术 第四章 组合量D 2.全加器 (Full Adder) 两个1位二进制数相加,考虑低位进位。 A;+B,+C-1(低位进位) =S:(和)→C:(向高位进位) A B C S; C A B( S;Ci 真值表 0 0 0 0n■a日8aa■s■aaa0■s■8级里■Bs8a0■8■a a■n88■■■sa0g■m■a0 Ssaas■a 8aa■■naa8里■ea00■■■aaa8■nanse0s8 面通■级面■量量面面面里组量细数面量组量■量组 0 0 1 ■面面■香道指■面■■用■原用海器 0 1 1 U 1 1 标准 S:=A B:Ci+A B:Ci+A:B:Ci+A B:Ci- 与或式 C;=A,B,C-1+A;B,C-1+A,B,C1+A,B,C-1
第四章 组合逻辑电路 2. 全加器(Full Adder) 两个 1 位二进制数相加,考虑低位进位。 Ai + Bi + Ci -1 ( 低位进位 ) = Si ( 和 ) Ci ( 向高位进位 ) 真 值 表 Si Ai Bi Ci-1 Ai Bi Ci-1 Ai Bi Ci-1 Ai Bi Ci-1 Ci Ai Bi Ci1 Ai Bi Ci1 Ai Bi Ci 1 Ai Bi Ci 1 标准 与或式 A B Ci-1 0 0 0 0 0 1 0 1 0 0 1 1 1 0 0 1 0 1 1 1 0 1 1 1 Si Ci A B Ci-1 Si Ci 0 0 1 0 1 0 0 1 1 0 0 1 0 1 1 1

数字电子技术 第四章组合} 全加器 (Full Adder) 卡诺图 00 011110 00011110 A A 0 最简与或式 圈“1=1瓦,C+iB,C+AaC+4BC C:=AB +ACi+B.Ci-
第四章 组合逻辑电路 卡诺图 全加器(Full Adder) A BC 0 1 00 01 11 10 1 1 1 1 Si A BC 0 1 00 01 11 10 1 1 1 1 Ci Si Ai Bi Ci-1 Ai Bi Ci-1 Ai Bi Ci-1 Ai Bi Ci-1 Ci Ai Bi Ai Ci1 Bi Ci1 最简与或式 圈 “ 1
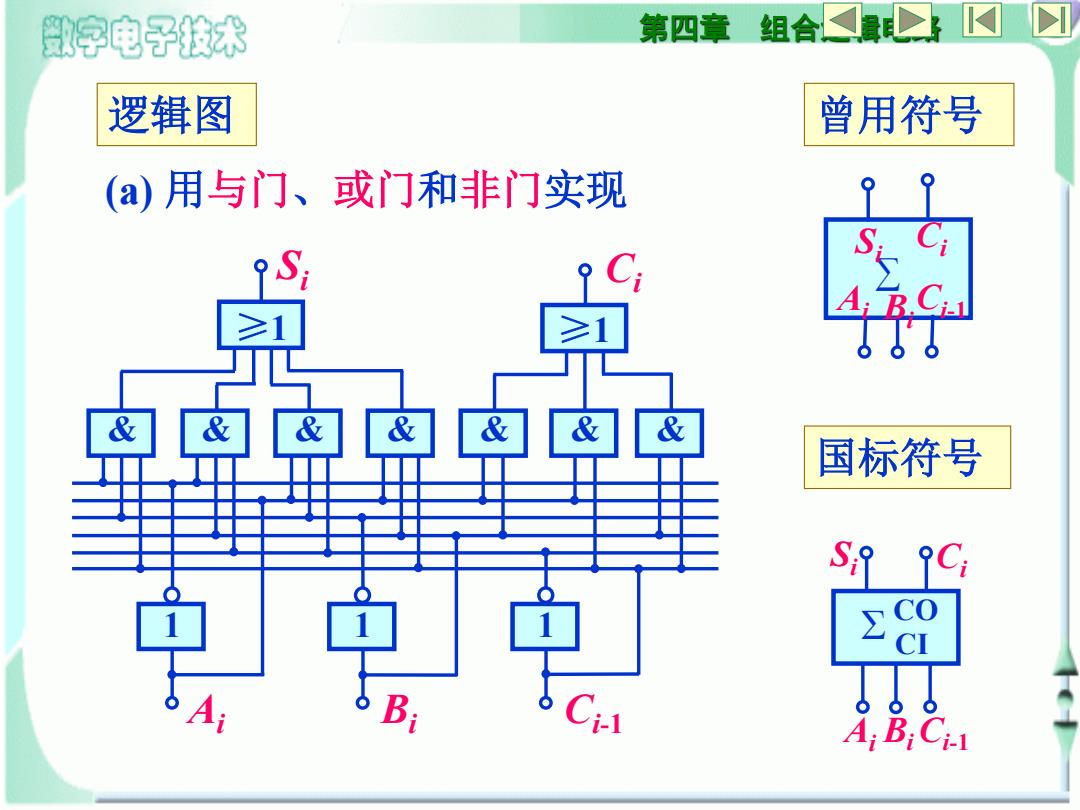
数字电子技术 第四章组合量} 逻辑图 曾用符号 (a)用与门、或门和非门实现 & & && & & & 国标符号 C 2 CI A:B:Ci
第四章 组合逻辑电路 逻辑图 (a) 用与门、或门和非门实现 曾用符号 国标符号 Σ CO CI Si Ai BiCi-1 Ci ∑ Si Ai Bi Ci-1 Ci & & & & & & & ≥1 1 1 1 Ai Si Ci Bi Ci-1 ≥1