
全程设计 章末核心素养整合
章末核心素养整合

知识体系构建 专题归纳突破
知识体系构建 专题归纳突破
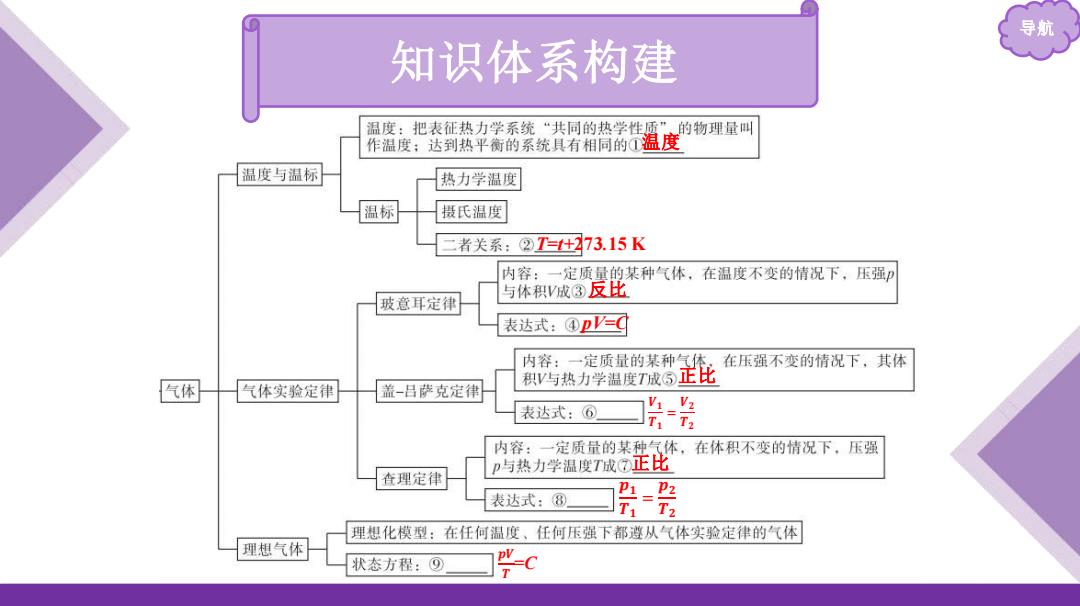
导航 知识体系构建 温度:把表征热力学系统“共同的热学性质”、的物理量叫 作温度;达到热平衡的系统具有相同的温度 温度与温标 热力学温度 温标 摄氏温度 二者关系:②T=+273.15K 内容:一定质量的某种气体,在温度不变的情况下,压强 与体积V成③反比 玻意耳定律 表达式:④pV匈 内容:一定质量的某种气体 在压强不变的情况下,其体 气体 气体实验定律 盖-吕萨克定律 积V与热力学温度T成⑤正比 表达式:⑥ 片号 内容:一定质量的某种气体, 在体积不变的情况下,压强 p与热力学温度T成⑦正比 查理定律 表达式:⑧ 片号 理想化模型:在任何温度、任何压强下都遵从气体实验定律的气体 理想气体 状态方程:⑨ c
导航 温度 T=t+273.15 K 反比 pV=C 正比 𝑽𝟏 𝑻𝟏 = 𝑽𝟐 𝑻𝟐 正比 𝒑𝟏 𝑻𝟏 = 𝒑𝟐 𝑻𝟐 𝒑𝑽 𝑻 =C 知识体系构建
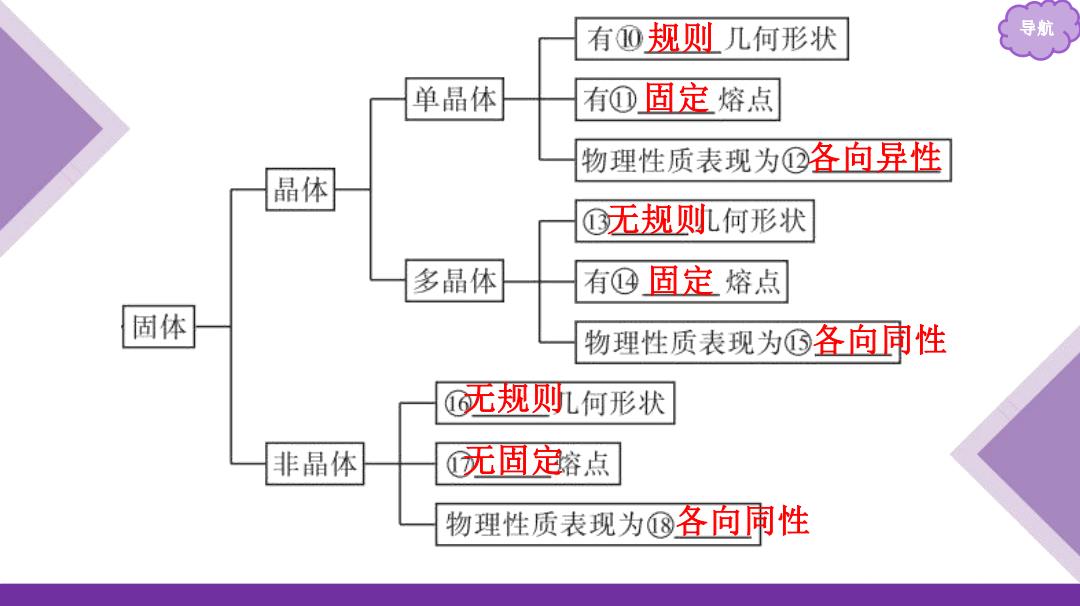
有⑩规则几何形状 导航 单晶体 有①固定熔点 物理性质表现为①各问异性 晶体 心无规则何形状 多晶体 有@固定熔点 固体 物理性质表现为⑤各向同性 无规则L何形状 非晶体 无固定容点 物理性质表现为⑧©各向南性
规则 导航 固定 各向异性 无规则 固定 各向同性 无规则 无固定 各向同性

导航 表面张力:在液体表面层内的各个方向上都存在,力的方向总是跟液面相切,且与分界面 ⑨垂直使液体表面绷紧的力 浸润、不浸润:一种液体会润湿某种固体并附着在固体的表面上的现象叫作浸润;不会润 湿某种固体,也就不会附着在这种固体的表面的现象叫作不浸润 液体 毛细现象:浸润液体在细管中@上升的现象,以及不浸润液体在细管中④下降的现象, 称为毛细现象 液晶:液晶是介于固态和液态之间的一种物质状态。液晶态既具有液体的②流动性,又 在一定程度上具有晶体分子的②③ 的性质 规则排列
导航 垂直 上升 下降 流动性 规则排列

导 专题归纳突破 专题一气体压强的计算方法 封闭气体压强的计算是应用气体实验定律的基础,大致可分 为液体封闭气体压强的计算和固体封闭气体压强的计算。 1.平衡时液体封闭气体压强的计算:液体封闭气体压强的计 算的典型问题是水银柱封闭气体压强的计算,常采用的方法 如下所示
导航 专题一 气体压强的计算方法 封闭气体压强的计算是应用气体实验定律的基础,大致可分 为液体封闭气体压强的计算和固体封闭气体压强的计算。 1.平衡时液体封闭气体压强的计算:液体封闭气体压强的计 算的典型问题是水银柱封闭气体压强的计算,常采用的方法 如下所示。 专题归纳突破

(1)取等压面法:根据同种液体在同一水平液面处压强相等 导航 在连通器内灵活选取等压面,由两侧压强相等列方程求解压 强。 如图所示,C、D在同一液面处,两点压强相等,所以封闭气体 的压强p=po+pgh(其中h为液面间的竖直高度差,不一定是液 柱的长度p为液体密度)。 B
导航 (1)取等压面法:根据同种液体在同一水平液面处压强相等, 在连通器内灵活选取等压面,由两侧压强相等列方程求解压 强。 如图所示,C、D在同一液面处,两点压强相等,所以封闭气体 的压强p=p0+ρgh(其中h为液面间的竖直高度差,不一定是液 柱的长度,ρ为液体密度)

(2)参考液片法:通常是在液体的最低点选取假想的液体薄 片(自身重力不计)为研究对象,分析液片两侧受力情况,建立 平衡方程消去面积,得到液片两侧压强相等,进而求得封闭气 体的压强。 如图所示,设U形管的横截面积为S,在其最低处取一液片B, 由其两侧受力平衡可知 pS+pghoS-poS+pghoS+pghS 即得p=po+pgh
导航 (2)参考液片法:通常是在液体的最低点选取假想的液体薄 片(自身重力不计)为研究对象,分析液片两侧受力情况,建立 平衡方程消去面积,得到液片两侧压强相等,进而求得封闭气 体的压强。 如图所示,设U形管的横截面积为S,在其最低处取一液片B, 由其两侧受力平衡可知 pS+ρgh0S=p0S+ρgh0S+ρghS 即得p=p0+ρgh

导 2.平衡时固体封闭气体压强的计算:固体封闭气体压强计算 的典型问题是汽缸和活塞封闭气体压强的计算,通常选活塞 或汽缸为研究对象,对其进行受力分析,列平衡方程求封闭气 体的压强。 3.容器加速运动时,封闭气体压强的计算:当容器加速运动时, 通常选与气体相关联的液体柱、固体等为研究对象,分析研 究对象的受力情况,再根据运动情况,运用牛顿第二定律列方 程,可求得封闭气体的压强
导航 2.平衡时固体封闭气体压强的计算:固体封闭气体压强计算 的典型问题是汽缸和活塞封闭气体压强的计算,通常选活塞 或汽缸为研究对象,对其进行受力分析,列平衡方程求封闭气 体的压强。 3.容器加速运动时,封闭气体压强的计算:当容器加速运动时, 通常选与气体相关联的液体柱、固体等为研究对象,分析研 究对象的受力情况,再根据运动情况,运用牛顿第二定律列方 程,可求得封闭气体的压强

【典型例题1】如图所示,一上端开口、下端封闭的 细长玻璃管竖直放置。玻璃管的下部封有长L,=25.0 cm的空气柱,中间有一段长L,=25.0cm的水银柱,上部空 气柱的长度l,=40.0cm。已知大气压强相当于75cm高 水银柱产生的压强。现将一活塞(图中未画出)从玻璃 管开口处缓慢往下推,使管下部空气柱长度变为 l1'=20.0cm。假设活塞下推过程中没有漏气,求活塞下 推的距离。 答案:15.0cm
导航 【典型例题1】如图所示,一上端开口、下端封闭的 细长玻璃管竖直放置。玻璃管的下部封有长l1 =25.0 cm的空气柱,中间有一段长l2 =25.0 cm的水银柱,上部空 气柱的长度l3 =40.0 cm。已知大气压强相当于75 cm高 水银柱产生的压强。现将一活塞(图中未画出)从玻璃 管开口处缓慢往下推,使管下部空气柱长度变为 l1 '=20.0 cm。假设活塞下推过程中没有漏气,求活塞下 推的距离。 答案:15.0 cm