
Regression Analysis y=Bo+Bx1+Bx2+...Bxk+u Estimation Econometrics 15-Zhuxi @SJTU 1
Econometrics 15 - Zhuxi @SJTU 1 Regression Analysis y = b0 + b1 x1 + b2 x2 + . . . bk xk + u Estimation

Some Terminology In the linear regression model,wherey=Bo+Bx +Bx2+...Bx+u,we typically call 1% xpx2...xk Dependent Variable Independent Variable Left-Hand Side Variable Right-Hand Side Variable Explained Variable Explanatory Variable Regressand Regressor Covariate,Control Variables Econometrics 15-Zhuxi @SJTU 2
Econometrics 15 - Zhuxi @SJTU 2 Some Terminology In the linear regression model, where y = b0 + b1 x1 + b2 x2 + . . . bk xk + u, we typically call y x1 ,x2 , …,xk Dependent Variable Independent Variable Left-Hand Side Variable Right-Hand Side Variable Explained Variable Explanatory Variable Regressand Regressor Covariate, Control Variables

2.1 Motivation for multiple regression We usually make Zero Conditional Mean Hypothesis: E(ux)=0,which implies E(ylx)=Bo+Bx1+B2x2+...Bxxk E(ux)=0 implies that the regression disturbance u contains no systematic information ofx that can be used to predict the mean of y. In other words,all information ofx that can be used to predict the expectation of y has been completely summarized. Econometrics 15-Zhuxi @SJTU 3
Econometrics 15 - Zhuxi @SJTU 3 2.1 Motivation for multiple regression We usually make Zero Conditional Mean Hypothesis: E(u|x) = 0, which implies E(y|x) = b0 + b1 x1 + b2 x2 + . . . bk xk E(u|x) = 0 implies that the regression disturbance u contains no systematic information of x that can be used to predict the mean of y. In other words, all information of x that can be used to predict the expectation of y has been completely summarized

Zero Conditional Mean Hypothesis (ctd) The condition E(ux)=0 is crucial for the validity of economic interpretation of model parameters-- correct model specification for E(vx) y=B。+Bx+B2x2+ If E(ux)=0,then- (y1x)=B 0x1 IfE(ux)=yx2≠0,then E(y)=B+27x 、 8x Econometrics 15-Zhuxi @SJTU 4
Econometrics 15 - Zhuxi @SJTU 4 Zero Conditional Mean Hypothesis (ctd) The condition E(u|x) = 0 is crucial for the validity of economic interpretation of model parameters -- correct model specification for E(y|x). 0 1 1 2 2 1 1 2 1 1 1 1 | If | 0, then . | If | 0, then 2 . y x x u E y x E u x x E y x E u x x x x b b b b b

Motivation of multiple regression For simple model:y=B+Beduc+u, It's unlikely that the condition E(u educ)=0 holds. Q:Why? A:Many important variables are omitted in u. Thus a multi model:y=Bo+Beduc+Bzexperience+u, where E(uleduc,experience)=0, may be more reasonable. Now,what's the economic meaning of B Econometrics 15-Zhuxi @SJTU 5
Econometrics 15 - Zhuxi @SJTU 5 Motivation of multiple regression Now, what’s the economic meaning of b1 . 0 1 0 1 2 For simple model: , It's unlikely that the condition | 0 holds. Q: Why? A: Many important variables are omitted in . Thus a multi model: , | , y educ u E u educ u y educ experience u where E u educ b b b b b 0, may be more reasonable. experience

Interpreting Multiple Regression Bo++Bxx So △少=B,△x+B2△x2+.+B△x, so holdingx2,fixed implies that △y=阝,△x,that is each B has a ceteris paribus interpretation (partial effect) Holding other factors fixed Econometrics 15-Zhuxi @SJTU 6
Econometrics 15 - Zhuxi @SJTU 6 Interpreting Multiple Regression 0 1 1 2 2 1 1 2 2 2 1 1 ˆ ˆ ˆ ˆ ˆ ... , so ˆ ˆ ˆ ˆ ... , so holding ,..., fixed implies that ˆ ˆ , that is each has a interpretation (partial effect) k k k k k y x x x y x x x x x y x ceteris paribus Holding other factor b b b b b b b b b s fixed

2.2 Mechanics and interpretation of OLS For convenience,we introduce matrix form,for =Bo+Bx.+Bx+u i=1,2....n we could write it in matrix form as follows Yx)B()np where Y=.)B=(BoBB) 1x1 X12..X 1 Xm(k+i) X21 X22 1 Xnl Xn2 Xnk Econometrics 15-Zhuxi @SJTU 7
Econometrics 15 - Zhuxi @SJTU 7 2.2 Mechanics and interpretation of OLS 0 1 1 1 1 1 1 1 1 1 2 0 1 1 1 1 For convenience, we introduce matrix form, for ... 1,2,... we could write it in matrix form as follows where , ,... , , ,..., , i i k ki i n n n k k n n k k n k y x x u i n Y X u Y y y y X b b b b b b b b , 11 12 1 21 22 1 2 1 1 1 k n n nk x x x x x x x x

Obtaining the OLS Estimates(ctd) the method of OLS(minimize SSR): min之td=∑(y-b。-bx:-b,x--bea)) bo,b,… il i- or in matrix form min SSR(b)=(Y-Xb)(Y-X6) Econometrics 15-Zhuxi @SJTU 8
Econometrics 15 - Zhuxi @SJTU 8 Obtaining the OLS Estimates(ctd) 0 1 2 2 0 1 1 2 2 , ,... the method of OLS (minimize SSR): min ... ˆ or in matrix form min n n i i i i k ki b b i=1 i=1 b u y b b x b x b x SSR b Y Xb Y Xb
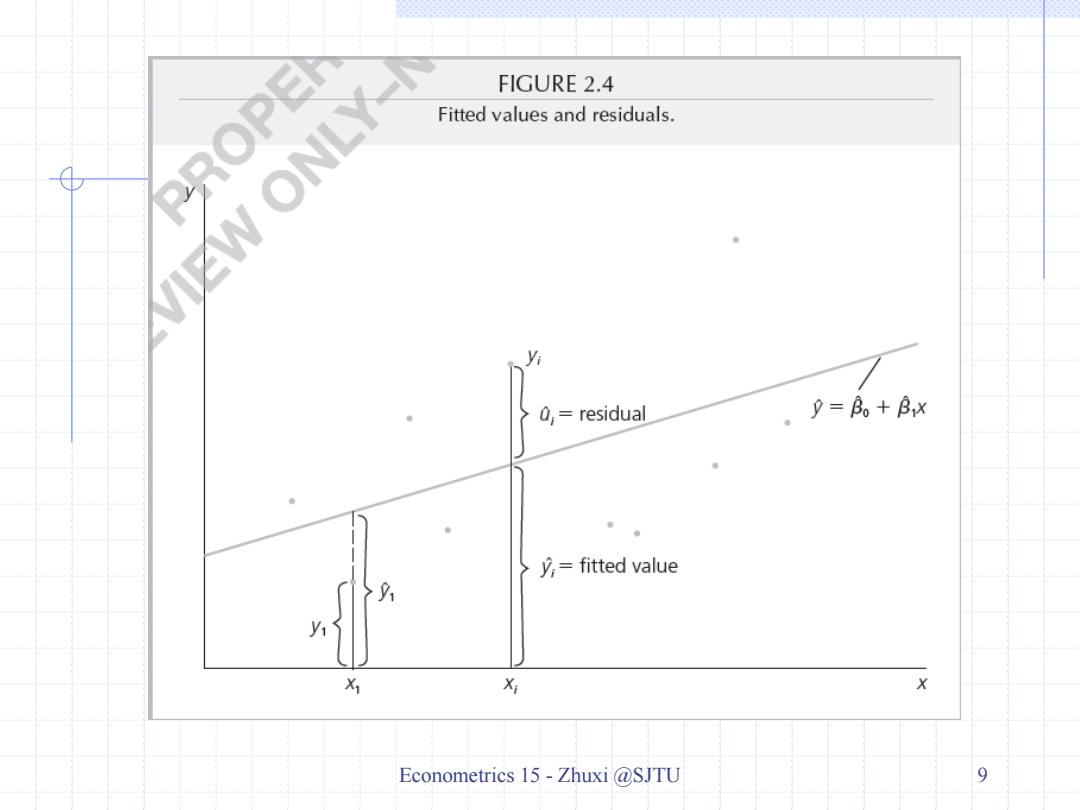
PROPEN FIGURE 2.4 W∠V ONLY- Fitted values and residuals. y 0,=residual ,9=B。+Bx y,=fitted value X X Econometrics 15-Zhuxi @SJTU 9
Econometrics 15 - Zhuxi @SJTU 9

Obtaining the OLS Estimates(ctd) by FOC on SSR(b),we have -2x(Y-XB)=0 or XXB=XY. by SOC,we have OSSR =2XX. aBaB assume XX is nonsingular,we have the OLS estimator B=(XX)XY. for simple regression,we have -Bx ∑(,-)y/∑(-)) Econometrics 15-Zhuxi @SJTU 10
Econometrics 15 - Zhuxi @SJTU 10 Obtaining the OLS Estimates(ctd) 1 0 2 1 by FOC on SSR , we have ˆ ˆ 2 0 or . by SOC, we have SSR 2 . ˆ ˆ assume is nonsingular, we have the OLS estimator ˆ . for simple regression, we have ˆ ˆ ˆ b X Y X X X X Y X X X X X X X Y b b b b b b b b 1 1 2 1 1 1 1 1 1 1 ˆ . n n i i i i i y x x x y x x b