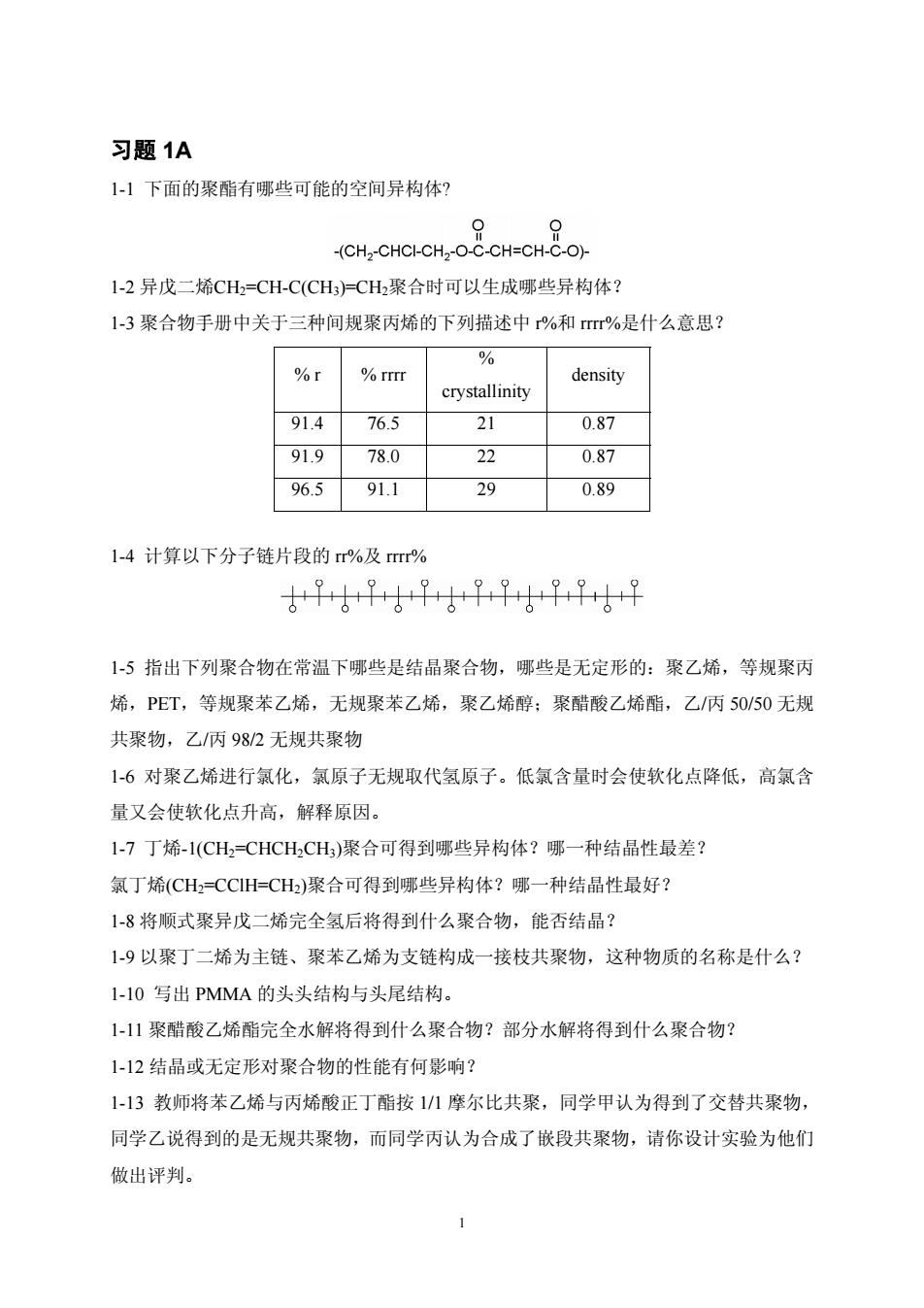
习题1A 1-1下面的聚酯有哪些可能的空间异构体? 1-2异戊二烯CH=CH-C(CH)CH聚合时可以生成哪些异构体? 13聚合物手册中关于三种间规聚丙烯的下列描述中r%和r%是什么意思? % %r %rrIr density crystallinity 91.476.5 21 0.87 91.9 78.0 0.87 96.591.1 29 0.89 1-4计算以下分子链片段的m%及m% ++甲+5中+早甲p+4 15指出下列聚合物在常温下哪些是结晶聚合物,哪些是无定形的:聚乙烯,等规聚丙 烯,PET,等规聚苯乙烯,无规聚苯乙烯,聚乙烯醇:聚醋酸乙烯酯,乙/丙50/50无规 共聚物,乙丙982无规共聚物 1-6对聚乙烯进行氯化,氯原子无规取代氢原子。低氯含量时会使软化点降低,高氯含 量又会使软化点升高,解释原因。 1-7丁烯-1(CH,-CHCH,CH)聚合可得到哪些异构体?哪一种结晶性最差? 氯丁烯(CH,-CCIH=CH2)聚合可得到哪些异构体?哪一种结晶性最好? 1-8将顺式聚异戊二烯完全氢后将得到什么聚合物,能否结晶? 1-9以聚丁二烯为主链、聚苯乙烯为支链构成一接枝共聚物,这种物质的名称是什么? 1-10写出PMMA的头头结构与头尾结构。 1-11聚醋酸乙烯酯完全水解将得到什么聚合物?部分水解将得到什么聚合物? 112结晶或无定形对聚合物的性能有何影响? 113教师将苯乙烯与丙烯酸正丁酯按11摩尔比共聚,同学甲认为得到了交替共聚物 同学乙说得到的是无规共聚物,而同学丙认为合成了嵌段共聚物,请你设计实验为他们 做出评判
习题 1A 1-1 下面的聚酯有哪些可能的空间异构体? 1-2 异戊二烯CH2=CH-C(CH3)=CH2聚合时可以生成哪些异构体? 1-3 聚合物手册中关于三种间规聚丙烯的下列描述中 r%和 rrrr%是什么意思? % r % rrrr % crystallinity density 91.4 76.5 21 0.87 91.9 78.0 22 0.87 96.5 91.1 29 0.89 1-4 计算以下分子链片段的 rr%及 rrrr% 1-5 指出下列聚合物在常温下哪些是结晶聚合物,哪些是无定形的:聚乙烯,等规聚丙 烯,PET,等规聚苯乙烯,无规聚苯乙烯,聚乙烯醇;聚醋酸乙烯酯,乙/丙 50/50 无规 共聚物,乙/丙 98/2 无规共聚物 1-6 对聚乙烯进行氯化,氯原子无规取代氢原子。低氯含量时会使软化点降低,高氯含 量又会使软化点升高,解释原因。 1-7 丁烯-1(CH2=CHCH2CH3)聚合可得到哪些异构体?哪一种结晶性最差? 氯丁烯(CH2=CClH=CH2)聚合可得到哪些异构体?哪一种结晶性最好? 1-8 将顺式聚异戊二烯完全氢后将得到什么聚合物,能否结晶? 1-9 以聚丁二烯为主链、聚苯乙烯为支链构成一接枝共聚物,这种物质的名称是什么? 1-10 写出 PMMA 的头头结构与头尾结构。 1-11 聚醋酸乙烯酯完全水解将得到什么聚合物?部分水解将得到什么聚合物? 1-12 结晶或无定形对聚合物的性能有何影响? 1-13 教师将苯乙烯与丙烯酸正丁酯按 1/1 摩尔比共聚,同学甲认为得到了交替共聚物, 同学乙说得到的是无规共聚物,而同学丙认为合成了嵌段共聚物,请你设计实验为他们 做出评判。 1

习题1B 1-14三个单分散聚苯乙烯样品混合:分子量10000的1g,分子量50000的2g,分子量 100000的2g。求混合物的数均、重均及Z均分子量。 115一聚合物具有下图中的分子量分布,求其数均、重均及Z均分子量。 10 10 分子量 1-l6聚合物A和B等重量混合,求混合物的Mw与Mn。A:M=35000,Mw=90000:B: Mm=150000,M=300000 1-17用硬脂酸钙(Ca(OOC(CH)16CHh)作为PVC加工润滑剂。含2wt%硬脂酸钙的PVC 体系的M。=90 00mol/g,求纯PVC的Mn。 1-18纯纤维素的经验式为CH1670o.3,平均分子量为1.46x103molg。采用分子量为 2.7×10mol/g的单分散聚丙烯腈在其上接枝,产物元素分析的结果为氨含量7.13wt%, 求每根纤维素分子链上接枝的丙烯腈链数 1-19端基分析得知尼龙6中-NH含量为4.45x10mol/g,求其平均聚合度 1-20将50g聚合物样品分成六个级分,测定各级分的数均分子量M如下: 级分号重量(g) Ma 1.5 2000 5.5 5000 22.0 100000 12.0 200000 45 500000 6 1.5 1000000 假定每级分是单分散的,求Mn与Mw。 1-21某种聚合物的重量分布函数为:w,=kx2,x=1,2,3,4,求数均聚合度x,重均聚合 度xw 1-22聚合物混合物由三个样品组成,计算混合物的Mn与Mw 2
习题 1B 1-14 三个单分散聚苯乙烯样品混合:分子量 10000 的 1g,分子量 50000 的 2g,分子量 100000 的 2g。求混合物的数均、重均及 Z 均分子量。 1-15 一聚合物具有下图中的分子量分布,求其数均、重均及 Z 均分子量。 1-16 聚合物A和B等重量混合,求混合物的Mw与Mn。A:Mn=35000,Mw=90000;B: Mn=150000,Mw=300000 1-17 用硬脂酸钙(Ca(OOC(CH2)16CH3)2)作为PVC加工润滑剂。含 2wt%硬脂酸钙的PVC 体系的Mn=9000mol/g,求纯PVC的Mn。 1-18 纯纤维素的经验式为CH1.67O0.83,平均分子量为 1.46×105 mol/g。采用分子量为 2.7×104 mol/g的单分散聚丙烯腈在其上接枝,产物元素分析的结果为氮含量 7.13wt%, 求每根纤维素分子链上接枝的丙烯腈链数。 1-19 端基分析得知尼龙 6 中-NH2含量为 4.45×10−5 mol/g,求其平均聚合度。 1-20 将 50g聚合物样品分成六个级分,测定各级分的数均分子量Mn如下: 级分号 重量(g) Mn 1 1.5 2000 2 5.5 5000 3 22.0 100000 4 12.0 200000 5 4.5 500000 6 1.5 1000000 假定每级分是单分散的,求Mn与Mw。 1-21 某种聚合物的重量分布函数为:wx = kx2 , x = 1,2,3,4,求数均聚合度xn,重均聚合 度xw。 1-22 聚合物混合物由三个样品组成,计算混合物的Mn与Mw。 2

样品号Mn Mw重量(g) A 1.2×1034.5×103 200 5.6×10 8.9x10 200 10.0×10310.0×10 100 习题2A 2-1某聚:烯烃的平均聚合度为500,均方末端距为165nm2,试求: ()Flory特征比C: (2)Kuhn长度b: (3)每个大分子平均包含的Kuhn单元: (4)每个Kuhn单元包含的重复结构单元数。 2-2今有大分子链a、b,分别含有p、q个自由连接的链段,链段长度均为L,现将b分 子接枝到a分子的正中。求从a分子的一端A到此支化分子的另二端A'及B的均方 末端距。 23今有大分子链a含有p个长度为L的链段,大分子链含有q个长度为M的链段, 均为自由连接链。现将b分子接枝到a分子的正中。求从AB链的均方末端距 24为什么聚合物在本体态的回转半径与0溶剂中相同而不同于其它溶剂中的值? 2-5求Me10gmol的聚乙烯在140C的均方末端距。 2.6证明自由连接链最可几末端距为(2l产/3)2。 2-7计算1000个下列重复单元组成的聚合物的伸展长度(忽略端基影响): (a)-(Si(CH3)2O)-(b)-(CH2-CO-O)-(c)-(CH2-CH2)-(d)-(CH2-O)- 2-8计算分子量为1x10的聚苯乙烯(C=9.85)的Kuhn长度。 2-9自由连接链A含x个长度为l,的链段,B含y个长度为,的链段,两根链末端对接,求 此结合链的均方末端距。 2-10聚合物稀溶液以npc对c作图得到直线,截距为1.50cm3/g,斜率为0.9cm/g2,求此 聚合物/溶剂对的Huggins常数。 2-11聚苯乙烯在25C四氢呋喃中Mark-Houwink常数为k-6.82x103cm3/g,a=0.766,相 同溶剂中PMMA具有[m=1.28×10M,6(cm/g)。利用以上数据构造以聚苯乙烯为标准 样品的、PMMA的GPC校正曲线
样品号 Mn Mw 重量(g) A 1.2×105 4.5×105 200 B 5.6×105 8.9×105 200 C 10.0×105 10.0×105 100 习题 2A 2-1 某聚α-烯烃的平均聚合度为 500,均方末端距为 165nm2 ,试求: (1) Flory 特征比C∞; (2) Kuhn 长度 b; (3) 每个大分子平均包含的 Kuhn 单元 z; (4) 每个 Kuhn 单元包含的重复结构单元数。 2-2 今有大分子链 a、b,分别含有 p、q 个自由连接的链段,链段长度均为 L,现将 b 分 子接枝到 a 分子的正中。求从 a 分子的一端 A 到此支化分子的另二端 A'及 B 的均方 末端距。 2-3 今有大分子链 a 含有 p 个长度为 L 的链段,大分子链含有 q 个长度为 M 的链段, 均为自由连接链。现将 b 分子接枝到 a 分子的正中。求从 AB 链的均方末端距。 2-4 为什么聚合物在本体态的回转半径与θ溶剂中相同而不同于其它溶剂中的值? 2-5 求M=107 g/mol的聚乙烯在 140°C的均方末端距。 2.6 证明自由连接链最可几末端距为 。2/12 nl )3/2( 2-7 计算 1000 个下列重复单元组成的聚合物的伸展长度(忽略端基影响): (a) –(Si(CH3)2O)- (b)-(CH2-CO-O)- (c) –(CH2-CH2)- (d) –(CH2-O)- 2-8 计算分子量为 1×105 的聚苯乙烯(C∞=9.85)的Kuhn长度。 2-9 自由连接链A含x个长度为la的链段,B含y个长度为lb的链段,两根链末端对接,求 此结合链的均方末端距。 2-10 聚合物稀溶液以ηsp/c对c作图得到直线,截距为 1.50cm3 /g,斜率为 0.9cm6 /g2 ,求此 聚合物/溶剂对的Huggins常数。 2-11 聚苯乙烯在 25°C四氢呋喃中Mark-Houwink常数为k=6.82×10−3 cm3 /g,α=0.766,相 同溶剂中PMMA具有[η]=1.28×10−2 Mη 0.69(cm3 /g)。利用以上数据构造以聚苯乙烯为标准 样品的、PMMA的GPC校正曲线。 3
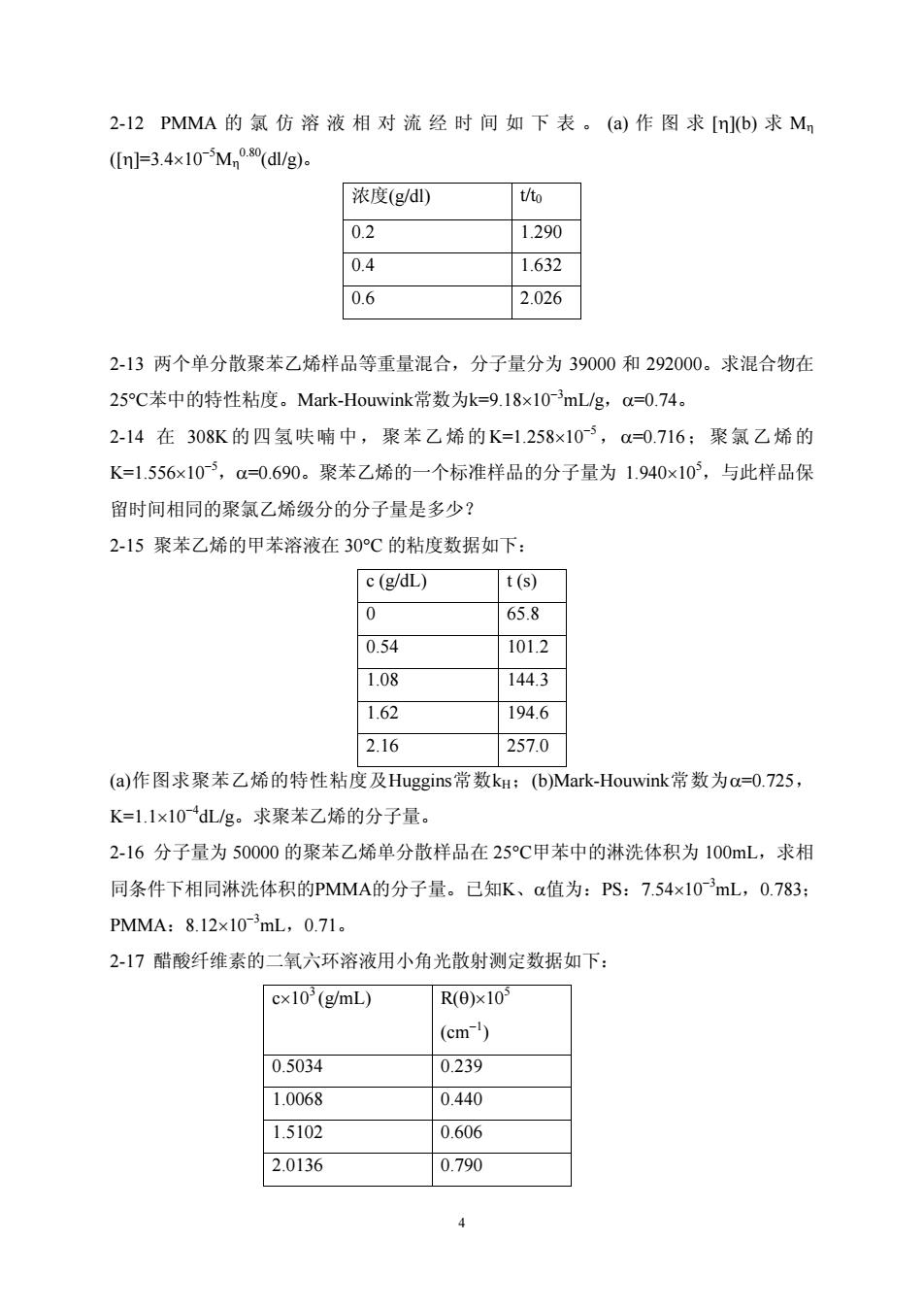
2-12PMMA的氯仿溶液相对流经时间如下表。(a)作图求[nb)求Mn (n=3.4x10M,0(dWg). 浓度(gdl t/to 02 1.290 0.4 1.632 0.6 2.026 2-13两个单分散聚苯乙烯样品等重量混合,分子量分为39000和292000。求混合物在 25C苯中的特性粘度。Mark-Houwink常数为k=9.18×10mL/g,a=0.74。 2-14在308K的四氢呋喃中,聚苯乙烯的K=1.258×10~3,a=0.716:聚氯乙烯的 K=1.556x105,a-=0.690。聚苯乙烯的一个标准样品的分子量为1.940×10,与此样品保 留时间相同的聚氯乙烯级分的分子量是多少? 2-15聚苯乙烯的甲苯溶液在30℃的粘度数据如下: c(g/dL) t(s) 0 65.8 0.54 101.2 1.08 144.3 1.62 194.6 2.16 257.0 (a)作图求聚苯乙烯的特性粘度及Huggins常数k:(b)Mark-Houwink常数为a=0.725, K=1.1x10dL/g。求聚苯乙烯的分子量 2-16分子量为50000的聚苯乙烯单分散样品在25℃甲苯中的淋洗体积为100mL,求相 同条件下相同淋洗体积的PMMA的分子量。已知K、a值为:PS:7.54x10mL,0.783: PMMA:8.12x103mL,0.71。 217醋酸纤维素的二氧六环溶液用小角光散射测定数据如下 cx10 (g/mL) R(0)x10 (cm) 0.5034 0239 1.0068 0.440 1.5102 0.606 2.0136 0.790
2-12 PMMA 的氯仿溶液相对流经时间如下表。 (a) 作图求 [η](b) 求 Mη ([η]=3.4×10−5 Mη 0.80(dl/g)。 浓度(g/dl) t/t0 0.2 1.290 0.4 1.632 0.6 2.026 2-13 两个单分散聚苯乙烯样品等重量混合,分子量分为 39000 和 292000。求混合物在 25°C苯中的特性粘度。Mark-Houwink常数为k=9.18×10−3 mL/g,α=0.74。 2-14 在 308K的四氢呋喃中,聚苯乙烯的K=1.258×10−5,α=0.716;聚氯乙烯的 K=1.556×10−5 ,α=0.690。聚苯乙烯的一个标准样品的分子量为 1.940×105 ,与此样品保 留时间相同的聚氯乙烯级分的分子量是多少? 2-15 聚苯乙烯的甲苯溶液在 30°C 的粘度数据如下: c (g/dL) t (s) 0 65.8 0.54 101.2 1.08 144.3 1.62 194.6 2.16 257.0 (a)作图求聚苯乙烯的特性粘度及Huggins常数kH;(b)Mark-Houwink常数为α=0.725, K=1.1×10−4 dL/g。求聚苯乙烯的分子量。 2-16 分子量为 50000 的聚苯乙烯单分散样品在 25°C甲苯中的淋洗体积为 100mL,求相 同条件下相同淋洗体积的PMMA的分子量。已知K、α值为:PS:7.54×10−3 mL,0.783; PMMA:8.12×10−3 mL,0.71。 2-17 醋酸纤维素的二氧六环溶液用小角光散射测定数据如下: c×103 (g/mL) R(θ)×105 (cm−1 ) 0.5034 0.239 1.0068 0.440 1.5102 0.606 2.0136 0.790 4

2.5170 0.902 已知二氧六环的折光指数o=1.4199,醋酸纤维素在三氧六环中的折光指数增率为 dndc=-6.297×102cmg,入射光波长.=632.8nm,求重均分子量及第二维利系数。 2-18用两种合成方法得到同一种聚合物,但分子量不同,分别为M和MB,特性粘度分 别为[ml和[B,建立一个方程描述这两种聚合物的共混物的特性粘度与共混组成间的 关系。 2-19在溶液中进行活性聚合,得到分子量为100000gmol的聚合物A,然后加入单体B。 后续的反应可能为继续活性聚合得到嵌段聚合物,也可能得到A、B两种聚合物的共混 物。B的均聚物分子量估计为15000g/mol。将产物用GPC进行鉴定,画出以下三种可 能的GPC谱图:(a)产物全为嵌段共聚物:(b)B单体一半构成嵌段共聚物一半形成均聚 物:(c)产物全为共混物 2-20合成了一种新聚合物,测得其特性粘度为5.5mLg,GPC测定的淋洗体积为160cm3。 利用下列普适校正曲线计算其分子量。 10 10 10 承荒体积Vcm 习题2B 2-21格子中有100个格位。计算()10个溶质分子在其中的摆放方式数。(b)含10个单 元的分子链的摆放方式数。 2-21计算(1)100个黑球和100个白球(2)10个由10个黑球组成的分子链和100个白球(3) 10个由10个黑球组成的分子链和10个由10个白球组成的分子链的混合嫡, 2-22将一摩尔M=2×10°gmol的聚苯乙烯与10m3的甲苯在298K混合,求混合自由能。 己知聚苯乙烯的密度为1.06gcm3,在甲苯中的x值为0.37。 2-23重叠浓度对分子量有何依赖性? 2-24分子量高于多少的聚氯乙烯不能气化?6=19.6Jcm)n,密度=136gem3
2.5170 0.902 已知二氧六环的折光指数n0=1.4199,醋酸纤维素在二氧六环中的折光指数增率为 dn/dc=6.297×10−2 cm3 /g,入射光波长λ=632.8nm,求重均分子量及第二维利系数。 2-18 用两种合成方法得到同一种聚合物,但分子量不同,分别为MA和MB,特性粘度分 别为[η]A和[η]B,建立一个方程描述这两种聚合物的共混物的特性粘度与共混组成间的 关系。 2-19 在溶液中进行活性聚合,得到分子量为 100000g/mol 的聚合物 A,然后加入单体 B。 后续的反应可能为继续活性聚合得到嵌段聚合物,也可能得到 A、B 两种聚合物的共混 物。B 的均聚物分子量估计为 15000g/mol。将产物用 GPC 进行鉴定,画出以下三种可 能的 GPC 谱图:(a)产物全为嵌段共聚物;(b)B 单体一半构成嵌段共聚物一半形成均聚 物;(c)产物全为共混物。 2-20 合成了一种新聚合物,测得其特性粘度为 5.5mL/g,GPC测定的淋洗体积为 160cm3 。 利用下列普适校正曲线计算其分子量。 习题 2B 2-21 格子中有 100 个格位。计算(a) 10 个溶质分子在其中的摆放方式数。(b)含 10 个单 元的分子链的摆放方式数。 2-21 计算(1)100个黑球和100个白球(2) 10个由10个黑球组成的分子链和100个白球(3) 10个由10个黑球组成的分子链和10个由10个白球组成的分子链的混合熵。 2-22 将一摩尔M=2×105 g/mol的聚苯乙烯与 10m3 的甲苯在 298K混合,求混合自由能。 已知聚苯乙烯的密度为 1.06g/cm3 ,在甲苯中的χ值为 0.37。 2-23 重叠浓度对分子量有何依赖性? 2-24 分子量高于多少的聚氯乙烯不能气化? δ= 19.6(J/cm3 ) 1/2,密度=1.36 g/cm3 。 5

2-25测得三己酸纤维素在二甲基甲酰胺中的0温度为41℃,并测得单位浓度的渗透压 πc=18.8Pa(gL),求三己酸纤维素的分子量。 2-26一聚合物溶液在25℃的渗透压如下: c(g/L) π(cm溶剂) 32 0.70 6.6 1.82 10 3.10 14 5.44 19 9.30 溶剂密度为0.85gcm3。(a)以π/RTc对浓度c作图;(b)计算聚合物的分子量及第二维利系 数。 2-27同一聚合物样品在渗透压测定中以πcT对c作图得到截距1M,在光散射测定中以 HcR-对c作图也得到截距1M,(a)两个1M是否相同?(b)两个斜率是否相同? 2-28A、B两种聚合物在27C的渗透压如下: CA(g/L) 渗透压πA,cm溶剂 Ca(g/L) 渗透压B,cm溶剂 3.20 0.70 6.60 1.82 4.0 1.60 10.0 3.10 9.0.0 4.44 14.0 5.44 14.0 8.95 19.0 9.30 18.0 13.01 溶剂密度为0.85,两种聚合物密度均为1.15。 (a)计算两种聚合物的M及第二维利系数。 (b)求A:B=25:75(wt)混合物的Mn。 (C)假定A、B两种聚合物的MMn均为2.O,求上述混合物的MwMn。 2-29从正则溶液模型导出旋节浓度的表达式。 习题2C 2-30某硫化橡胶的摩尔质量M=5000,密度p=1.0Mgm3,现于T=300K时将其拉伸 倍,求试样的回缩应力σ与弹性模量E。 6
2-25 测得三己酸纤维素在二甲基甲酰胺中的θ温度为 41°C,并测得单位浓度的渗透压 π/c=18.8Pa/(g/L),求三己酸纤维素的分子量。 2-26 一聚合物溶液在 25°C 的渗透压如下: c (g/L) π (cm 溶剂) 3.2 0.70 6.6 1.82 10 3.10 14 5.44 19 9.30 溶剂密度为 0.85g/cm3 。(a)以π/RTc对浓度c 作图;(b)计算聚合物的分子量及第二维利系 数。 2-27 同一聚合物样品在渗透压测定中以π/cRT对c作图得到截距 1/M,在光散射测定中以 Hc/Rθ=0对c 作图也得到截距 1/M,(a)两个 1/M是否相同?(b) 两个斜率是否相同? 2-28 A、B 两种聚合物在 27°C 的渗透压如下: CA(g/L) 渗透压πA,cm溶剂 CB(g/L) 渗透压πB,cm溶剂 3.20 0.70 6.60 1.82 4.0 1.60 10.0 3.10 9.0.0 4.44 14.0 5.44 14.0 8.95 19.0 9.30 18.0 13.01 溶剂密度为 0.85,两种聚合物密度均为 1.15。 (a)计算两种聚合物的Mn及第二维利系数。 (b)求A:B=25:75(wt)混合物的Mn。 (c)假定A、B两种聚合物的Mw/Mn均为 2.0,求上述混合物的Mw/Mn。 2-29 从正则溶液模型导出旋节浓度的表达式。 习题 2C 2-30 某硫化橡胶的摩尔质量Mc= 5000,密度ρ =1.0Mg/m3 ,现于T = 300K时将其拉伸一 倍,求试样的回缩应力σ与弹性模量E。 6

2-31密度为0.95Mgm3的理想弹性体,起始平均分子量为105,交联后交联点间的分子 量M为5×103,无交联缺陷,只考虑链末端校正,求其室温(300K)下的剪切模量。 2-32橡胶带截面积为10mm2,使用10N外力可在300K产生100%的伸长。求单位体积 中的网链数(Boltzmann?常数k=1.38×10-2J/K). 2-33橡胶带初始截面积为15mm×1.5mm,用10N外力在300K拉至初始长度的3倍。设 橡胶密度为0.9gcm3,求平均网链分子量。 2-34一根1×1x10cm3的橡胶带在1.5x10Pa的应力下在25C下拉伸到25cm长。 (a)设网络官能度为4,求交联点密度。 (b)在25℃下拉伸到15cm长时应力为多少? (C)在100C下拉伸到25cm长时应力为多少? 2-35一硫化天然橡胶在甲苯中溶胀到原体积的5倍。求溶胀前25℃下的模量。已知 X=0.39,甲苯的摩尔体积为106.3 cm/mol。. 2-36一根1×1x10cm3的橡胶带的杨氏模量为3x10Pa,其剪切模量为多少?在100C下 拉伸到25cm长所需应力为多少? 2-37两根长度为10cm橡胶的橡胶带被首尾相接在一起并固定在40cm的总长。让A带 处于25℃而B带处于150C,求B带的长度。 2-38SBR橡胶中苯乙烯含量为0.98mol%,交联前M,=100000。交联后密度为0.98gcm3求 25℃下100%拉伸应力及低拉伸时的模量。(a)网链分子量为10000:(b)网链分子量为 5000. 2-39一理想橡胶于27℃在一定应力作用下伸展到原长的1.10倍。10天后伸长不变情 况下127C的应力只剩10MPa。如果最初橡胶中交联密度为每单位体积0.015mol,求 10天后的交联密度。 2-40交联聚氧化丙烯-(CH,CH(CH)Oy中交联点间距为5000主链原子,密度为 1.20gcm3.今有一溶剂,密度为0.80gcm3,分子量为102,X=0.40。求聚合物在该溶剂 中溶胀后的密度。 2-41季戊四醇1mol与异氰酸酯2mol作用生成网络聚合物。 N=C=O C-(CH2OH)+2R →聚合物网络 N=C=0 密度为1.05gcm3。元素分析得知氮含量为2.10gL。将1.00cm3的这种聚合物用氯苯(密
2-31 密度为 0.95Mg/m3 的理想弹性体,起始平均分子量为 105,交联后交联点间的分子 量Mc为 5×103,无交联缺陷,只考虑链末端校正,求其室温(300K)下的剪切模量。 2-32 橡胶带截面积为 10mm2 ,使用 10N外力可在 300K产生 100%的伸长。求单位体积 中的网链数(Boltzmann常数k=1.38×10−23J/K)。 2-33 橡胶带初始截面积为 15mm×1.5mm,用 10N外力在 300K拉至初始长度的 3 倍。设 橡胶密度为 0.9g/cm3 ,求平均网链分子量。 2-34 一根 1×1×10cm3 的橡胶带在 1.5×104 Pa的应力下在 25°C下拉伸到 25cm长。 (a) 设网络官能度为 4,求交联点密度。 (b) 在 25°C 下拉伸到 15cm 长时应力为多少? (c) 在 100°C 下拉伸到 25cm 长时应力为多少? 2-35 一硫化天然橡胶在甲苯中溶胀到原体积的 5 倍。求溶胀前 25°C下的模量。已知 χ=0.39,甲苯的摩尔体积为 106.3cm3 /mol。 2-36 一根 1×1×10cm3 的橡胶带的杨氏模量为 3×104 Pa,其剪切模量为多少?在 100°C下 拉伸到 25cm长所需应力为多少? 2-37 两根长度为 10cm 橡胶的橡胶带被首尾相接在一起并固定在 40cm 的总长。让 A 带 处于 25°C 而 B 带处于 150°C,求 B 带的长度。 2-38 SBR橡胶中苯乙烯含量为 0.98mol%,交联前Mn=100000。交联后密度为 0.98g/cm3 求 25°C下 100%拉伸应力及低拉伸时的模量。(a)网链分子量为 10000;(b) 网链分子量为 5000。 2-39 一理想橡胶于 27°C 在一定应力作用下伸展到原长的 1.10 倍。10 天后伸长不变情 况下 127°C 的应力只剩 10MPa。如果最初橡胶中交联密度为每单位体积 0.015mol,求 10 天后的交联密度。 2-40 交联聚氧化丙烯-(CH2CH(CH3)O)-中交联点间距为 5000 主链原子,密度为 1.20g/cm3 。今有一溶剂,密度为 0.80g/cm3 ,分子量为 102,χ=0.40。求聚合物在该溶剂 中溶胀后的密度。 2-41 季戊四醇 1mol 与异氰酸酯 2mol 作用生成网络聚合物。 密度为 1.05g/cm3 。元素分析得知氮含量为 2.10g/L。将 1.00cm3 的这种聚合物用氯苯(密 7

度1.10gcm3,分子量112.5)溶胀至平衡。己知聚合物/溶剂间作用参数x=0.43,求最后溶 胀体积。 2-42交联聚氧化丙烯-(CH2CH(CH)Oy中交联点间距为3000个主链原子,密度为 1.20gcm3。今有一溶剂,密度为0.80gcm3,分子量为102,X=0.40。求聚合物形成的平 衡溶胀网络的密度。 习题3A 3-1根据下列数据求分子量无穷大聚合物的Tg。 T.K)182278354361362369.5375.5 M(gmol50010004000500060001000020000 3-2聚苯乙烯的Tg=100℃,聚丁二烯(视为均聚物)的Tg=-70°℃,欲得到T为-55C的了 苯橡胶,苯乙烯含量应为多少%? 3-3聚氯乙烯的Tg=356K,增塑剂的Tg=188K,求将PVC的Tg降至30C所用增塑剂的重 量分数。 3-4由式(3-36)的Taylor-Gordon公式,(a)证明Tg-Tgw,w2=k(TgT) (b)下表为PMMA(I)与环氧树脂(2)共混物的数据,利用表中数据以[(Tg1-Tgww]对 (TgT2)作图求出k值。T1=113C,T2=-19C. W2 Tg,℃ 0.000 113 0.200 52 0.300 42 0.430 0.700 3 1.000 -19 3-5单体A均聚物的玻璃化温度为60C,A和B的交替共聚物的玻璃化温度为-30C, 求B单体均聚物的玻璃化温度。 3-6苯乙烯均聚物的T为100C,苯乙烯丁二烯(25/75wMw)共聚物的T为-60℃,苯乙烯 丁二烯(75/25w小w)共聚物的Tg为28C,醋酸乙烯酯均聚物的T为28C。求丁二烯/醋酸 乙烯酯(50/50ww)共聚物的Tg。假设共聚物的T符合Gorden--Taylor方程,且含丁二烯的 共聚物k值均相同
度 1.10g/cm3 ,分子量 112.5)溶胀至平衡。已知聚合物/溶剂间作用参数χ=0.43,求最后溶 胀体积。 2-42 交联聚氧化丙烯-(CH2CH(CH3)O)-中交联点间距为 3000 个主链原子,密度为 1.20g/cm3 。今有一溶剂,密度为 0.80g/cm3 ,分子量为 102,χ=0.40。求聚合物形成的平 衡溶胀网络的密度。 习题 3A 3-1 根据下列数据求分子量无穷大聚合物的Tg。 Tg(K) 182 278 354 361 362 369.5 375.5 M(g/mol) 500 1000 4000 5000 6000 10000 20000 3-2 聚苯乙烯的Tg=100°C,聚丁二烯(视为均聚物)的Tg =−70°C,欲得到Tg为−55°C的丁 苯橡胶,苯乙烯含量应为多少wt%? 3-3 聚氯乙烯的Tg=356K,增塑剂的Tg=188K,求将PVC的Tg 降至 30°C所用增塑剂的重 量分数。 3-4 由式(3-36)的Taylor-Gordon公式,(a)证明(Tg1-Tg)w1/w2=k(Tg-Tg2) (b)下表为PMMA(1)与环氧树脂(2)共混物的数据,利用表中数据以[(Tg1-Tg)w1/w2]对 (Tg-Tg2)作图求出k值。Tg1=113°C,Tg2=-19°C。 w2 Tg,°C 0.000 113 0.200 52 0.300 42 0.430 11 0.700 -3 1.000 -19 3-5 单体 A 均聚物的玻璃化温度为 60°C,A 和 B 的交替共聚物的玻璃化温度为−30°C, 求 B 单体均聚物的玻璃化温度。 3-6 苯乙烯均聚物的Tg为 100°C,苯乙烯/丁二烯(25/75w/w)共聚物的Tg为−60°C,苯乙烯 /丁二烯(75/25w/w)共聚物的Tg为 28°C,醋酸乙烯酯均聚物的Tg为 28°C。求丁二烯/醋酸 乙烯酯(50/50w/w)共聚物的Tg。假设共聚物的Tg符合Gorden-Taylor方程,且含丁二烯的 共聚物k值均相同。 8

习题3B 3-7在三元件模型上突加应力时瞬时应变为0.002,1000s后应变为0.004,长时间后应 变趋向0.006。求推迟时间t 3-8一聚合物应力松弛模量在=0时为2.0GPa,=10s时为1.0GPa,求该聚合物突加应 力100MPa后1000s时的应变。 3-9一聚合物样品可用Kelvin模型描述,其弹簧模量为lMPa,粘壶粘度为100Pa.s,计 算下列条件下的伸长:(a)t=0时刻加载荷0.1kg,t=40s时除去载荷,=80s时重新施 加载荷0.1kg,120时再除去载荷,求t240s时的伸长:(b)0时刻加载荷0.1kg, =40s时再加载荷0.2kg,=200s时完全除去载荷,求=80s时的伸长。 3-10 Maxwell模型的弹簧模量为10Pa,粘壶粘度为101Pa.s.t=0时刻施加应变1%,25s 时再加应变2%,计算=50s时的应力。 3-11利用四元件模型,导出下列过程中应变与时间的函数关系: t<0g=0 0≤t<t=o0(蠕变) tst<t σ=0(蠕变回复) 3-12一聚合物可用Maxwell模型描述。103Pa的张力施加10s时,所得最大长度为初始长 度的1.15倍。去除应力10s后,长度变成初始长度的1.10倍。求该模型的松弛时 3-13一个类Maxwell单元由一个普通粘壶和一根理想橡胶带构成。27C时受1000Pa 的恒定应力,3h后应变为=2.00。在此刻去除应力,永久应变为0.750。现将此模型用 于应力松弛实验,在127C固定应变为1.5,求初始应力。 3-14一个SBR橡胶球的热容为Cp=1.83kkgK,从1米的高度落下回弹到60cm,假定 地板为理想弹性体,问球的温度升高多少? 3-15一线形无定形聚合物的玻璃化温度为10°C,25C时其粘度为6x10Pa.s,求其在40℃ 下的粘度。 3-16聚苯乙烯的玻璃化温度为100℃,求其在150的平移因子ar。(a)利用普适常数C,与 C2:(b)利用报道的常数C1=13.7与C2=50.0K。 3-17新合成一种热塑性聚合物,140C下的粘度为10Pa.s,玻璃化温度为Tg=110°℃, 9
习题 3B 3-7 在三元件模型上突加应力时瞬时应变为 0.002,1000s 后应变为 0.004,长时间后应 变趋向 0.006。求推迟时间τ。 3-8 一聚合物应力松弛模量在t=0 时为 2.0GPa,t=104 s时为 1.0GPa,求该聚合物突加应 力 100MPa后 1000s时的应变。 3-9 一聚合物样品可用 Kelvin 模型描述,其弹簧模量为 1MPa,粘壶粘度为 100Pa.s,计 算下列条件下的伸长:(a)t=0 时刻加载荷 0.1kg,t=40s 时除去载荷,t=80s 时重新施 加载荷 0.1kg,t=120 时再除去载荷,求 t=240s 时的伸长;(b) t=0 时刻加载荷 0.1kg, t=40s 时再加载荷 0.2kg,t=200s 时完全除去载荷,求 t=80s 时的伸长。 3-10 Maxwell模型的弹簧模量为108 Pa,粘壶粘度为1010Pa.s。t=0时刻施加应变1%, t=25s 时再加应变 2%,计算t=50s时的应力。 3-11 利用四元件模型,导出下列过程中应变与时间的函数关系: t < 0 σ = 0 0 ≤ t < t1 σ = σ0 (蠕变) t1 ≤ t < t2 σ = 0 (蠕变回复) 3-12 一聚合物可用Maxwell模型描述。103 Pa的张力施加 10s时,所得最大长度为初始长 度的 1.15 倍。去除应力 10s后,长度变成初始长度的 1.10 倍。求该模型的松弛时 间。 3-13 一个类 Maxwell 单元由一个普通粘壶和一根理想橡胶带构成。27°C 时受 1000Pa 的恒定应力,3h 后应变为ε=2.00。在此刻去除应力,永久应变为 0.750。现将此模型用 于应力松弛实验,在 127°C 固定应变为 1.5,求初始应力。 3-14 一个SBR橡胶球的热容为Cp=1.83kJkg−1 K−1 ,从 1 米的高度落下回弹到 60cm,假定 地板为理想弹性体,问球的温度升高多少? 3-15 一线形无定形聚合物的玻璃化温度为 10°C,25°C时其粘度为 6×107 Pa.s,求其在 40°C 下的粘度。 3-16 聚苯乙烯的玻璃化温度为 100°C,求其在 150°的平移因子aT。(a)利用普适常数C1与 C2;(b) 利用报道的常数C1=13.7 与C2=50.0K。 3-17 新合成一种热塑性聚合物,140°C下的粘度为 105 Pa.s,玻璃化温度为Tg=110°C, 9

(a)求这种聚合物在160C下的粘度: b)如何降低该聚合物的粘度? 习题3C 3-20为什么流道越长出口膨胀程度越低? 3-21一个塑料挤出机最适合2×10Pa.s的熔体粘度,某聚合物DPw=700在145C符合这个 粘度,其Tg=75C,每链节两个主链原子。由于工作不慎,聚合得到的该聚合物DPw=500, 问最佳挤出温度应是多少? 3-22用锥板粘度计测定粘度时,锥与板会受压相互靠近,还是被相互推开,还是会受侧 向力而错位? 3-23某新型聚合物链节含5个原子,链节分子量为211gmol,重均分子量为300000gmol, 其熔体粘度为1500泊。如果其分子量加倍,其熔体粘度应为多少? 3-24剪切应力与剪切速率子的关系可用一双参数经验公式表示:11+、8 Ay 某样品零切粘度为10Pa.s,应力为103Pa时的粘度为1.0Pa.5。求剪切速率为4x103s 时的粘度。 3-25一聚合物溶液可用x=2.70×1020635描述。应力为1000Pa时的粘度是多少mPas? 溶液为膨胀体、假塑体、触变体还是流凝体? 3-26某聚合物熔体可用模型产=2.00×1022描述。体积为0.500cm3该熔体被置于间距 为0.0100cm的两平板之间,其中动板被0.500g的重物拖动,求10s后动板移动的 距离。 习题4 4-1利用Thompson=-Gibbs方程计算厚度为100nm、50nm、l0nm、5nm的聚乙烯晶片的 熔点,△h°=293J/g,pe=lg/cm3,Tm°=415K,=90ml/m2。 4-2证明重量结晶度W。=A(1-Pp),其中A依赖聚合物性质,与结晶度无关,Pa与P,分 别为无定形组分与样品密度。今有两个聚合物样品密度分别为1.346和1.392gcm3, 重量结晶度分别为10%和50%。求(a)晶区与非晶区密度p.与Pa:(b)密度为1.357 10
(a)求这种聚合物在 160°C 下的粘度; (b)如何降低该聚合物的粘度? 习题 3C 3-20 为什么流道越长出口膨胀程度越低? 3-21 一个塑料挤出机最适合 2×104 Pa.s的熔体粘度,某聚合物DPw=700 在 145°C符合这个 粘度,其Tg=75°C,每链节两个主链原子。由于工作不慎,聚合得到的该聚合物DPw=500, 问最佳挤出温度应是多少? 3-22 用锥板粘度计测定粘度时,锥与板会受压相互靠近,还是被相互推开,还是会受侧 向力而错位? 3-23某新型聚合物链节含5个原子,链节分子量为211g/mol,重均分子量为300000g/mol, 其熔体粘度为 1500 泊。如果其分子量加倍,其熔体粘度应为多少? 3-24 剪切应力τ与剪切速率γ&的关系可用一双参数经验公式表示: γ γ τ & & B A + = 1 某样品零切粘度为 10Pa.s,应力为 103 Pa时的粘度为 1.0Pa.s。求剪切速率为 4×103 s -1 时的粘度。 3-25 一聚合物溶液可用 描述。应力为 1000Pa 时的粘度是多少 mPa.s? 溶液为膨胀体、假塑体、触变体还是流凝体? 635.02 τ ×= 1070.2 γ& 3-26 某聚合物熔体可用模型 描述。体积为 0.500cm 22 γ 1000.2 τ − & ×= 3 该熔体被置于间距 为 0.0100cm的两平板之间,其中动板被 0.500g的重物拖动,求 10s后动板移动的 距离 。 习题 4 4-1 利用Thompson=Gibbs方程计算厚度为 100nm、50nm、10nm、5nm的聚乙烯晶片的 熔点,Δh0 =293J/g,ρc=1g/cm3 ,Tm 0 =415K,σ=90mJ/m2 。 4-2 证明重量结晶度Wc=A(1−ρa/ρs),其中A依赖聚合物性质,与结晶度无关,ρa与ρs分 别为无定形组分与样品密度。今有两个聚合物样品密度分别为 1.346 和 1.392g/cm3 , 重量结晶度分别为 10%和 50%。求(a)晶区与非晶区密度ρc与ρa; (b)密度为 1.357 10