
第八章束流传输元器件和对应的传输矩阵 ·8.1概述及标准运动方程的解 ·8.2四极透镜 ·8.3弯转磁铁及其边缘场 ·8.4色散函数和包络函数 2
2 第八章 束流传输元器件和对应的传输矩阵 • 8.1 概述及标准运动方程的解 • 8.2 四极透镜 • 8.3 弯转磁铁及其边缘场 • 8.4 色散函数和包络函数
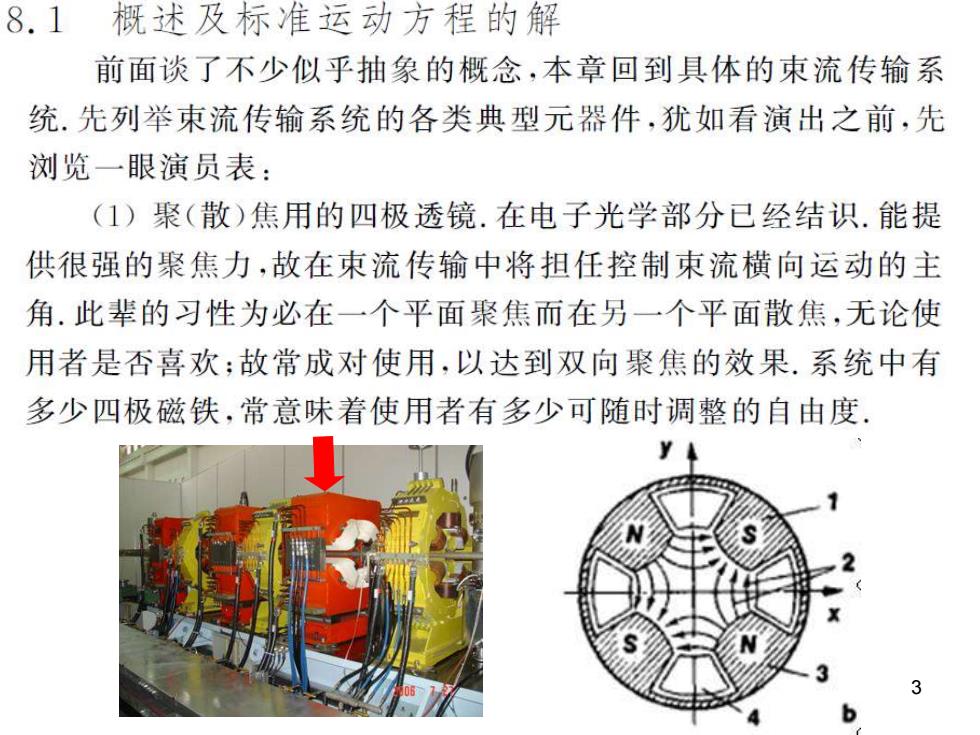
8.1概述及标准运动方程的解 前面谈了不少似乎抽象的概念,本章回到具体的束流传输系 统.先列举束流传输系统的各类典型元器件,犹如看演出之前,先 浏览一眼演员表: (1)聚(散)焦用的四极透镜.在电子光学部分已经结识.能提 供很强的聚焦力,故在束流传输中将担任控制束流横向运动的主 角.此辈的习性为必在一个平面聚焦而在另一个平面散焦,无论使 用者是否喜欢:故常成对使用,以达到双向聚焦的效果.系统中有 多少四极磁铁,常意味着使用者有多少可随时调整的自由度
3
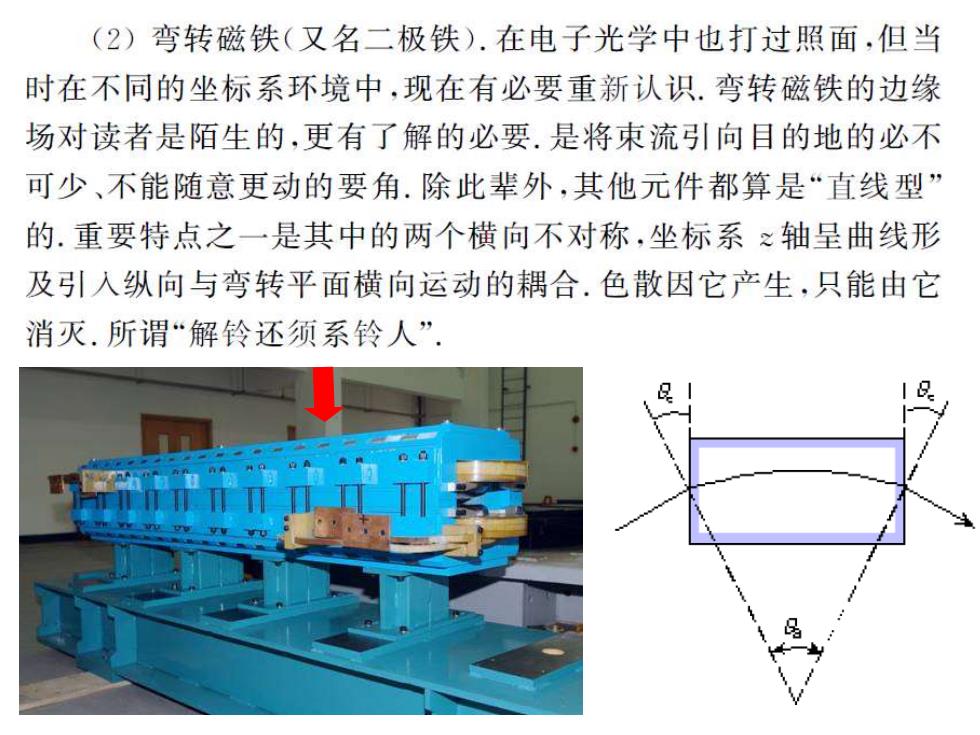
(2)弯转磁铁(又名二极铁).在电子光学中也打过照面,但当 时在不同的坐标系环境中,现在有必要重新认识.弯转磁铁的边缘 场对读者是陌生的,更有了解的必要.是将束流引向目的地的必不 可少、不能随意更动的要角.除此辈外,其他元件都算是“直线型” 的.重要特点之一是其中的两个横向不对称,坐标系之轴呈曲线形 及引入纵向与弯转平面横向运动的耦合.色散因它产生,只能由它 消灭.所谓“解铃还须系铃人
4

(3)有加速作用的元件.不是本课程重点.可分成两类,其一 是绝对的加速元件,束流质心动量P。通过它后有所增加,此类实 际上把系统分成两段粒子能量不同的传输系统,应分别处理(加速 中的横向运动则应以电子光学中介绍过的物理相空间方法处理): 其二是质心动量不变、而对纵向运动参量和δ进行调整的元 件,第9章将稍作介绍. (4)漂移空间.各主要元件之间的无场空间.看似“群众演 员”,往往不可缺少.其长度确定了其他元件的位置,常在设计一系 统时作为可调参数.又是各种辅助元件的寄身之地.长的传输系统 当然多半由漂移空间组成.在某种意义上,聚焦元件的功能就是为 束流做好准备,使它能穿过前方的漂移空间.束流在其中的表现特 点当然值得了解. 5
5

(5)磁铁制造、安装误差造成的场偏差或非理想场.其存在非 设计者所愿,但其影响不能忽视.是会形成中心轨道畸变、聚焦力 偏差、各种耦合、高阶场非线性效应等“恶果”的反面角色.多极磁 铁磁场和轴向磁场作为非理想场,亦归入此类, (6)测量元件和校正元件.本课程不可能对束流测量做详细 介绍.这两种元件的作用、其相互关系及与上一项各种误差的关系 是容易理解的.误差种类繁多,校正手法也不同.校正元件场与误 差场的相似之处是进行理想设计时皆不存在,须根据误差情况因 应设置,且非理想场误差多半只有非理想场方能矫正,所谓“以毒 攻毒”.它们的另一共同点是往往皆被视为没有长度的薄透镜! (7)其他元件.例如限制束流的光阑(束流传输中称刮束器或 限束狭缝)等. 6
6

这些典型元器件可分成两大类,以便进行数学处理.一类是 “有限长度器件”,或称“厚器件”,其中的场假设满足“区间常数”条 件,可逐元件地用解析法计算各元件对应的传输矩阵.另一类是 “无长度器件”,即薄透镜,其中的场可用“冲量假设”处理,对应的 传输矩阵就是“元传输矩阵”,但对若干可看作♂函数的量求积分. 之所以如此,可能是因为其作用区间确实很短,也可能因为其相对 强度较弱,可以把该场看作微扰,更准确的数学处理有难度或无 必要 大多数“有限长度器件”中的粒子运动方程就是上一章中的理 想场标准运动方程: "+Fu(z)·u=Gu()·δ z'=-G(》·u+ d 式中,u=x或y.F,G在有效长度L内(≤≤十L)视为常 数,其含义见前文
7

F-K+G ”+F.·u=Gw·8 Fy=-K+G2 '=-(G.·x+G,·y)+8 K- 1 ∂B (Bo)。axJo G=1 By (Bo)o G=一1 B Py (B0) 上一章已论述过,前一方程的通解应能写成u=·w十u ·十δ·和这3个数学特解函数,s,的性质,包括它们 满足的方程和初始条件. 为寻求各特解函数在区间常数条件下的数学形式,不妨根据 其初始条件与参量F.和G都不随之变化的特点,用级数展开法 求解.其结果可写成如下3个特殊函数:
8
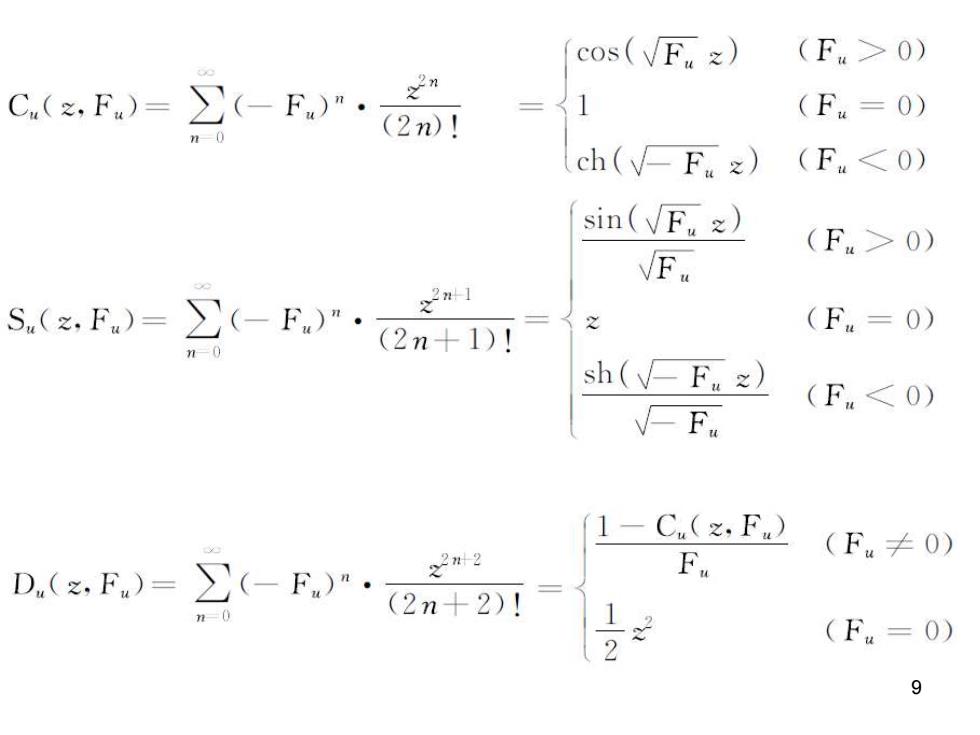
cos(Fz) (F.>0) C)=(-· (F4=0) ch(v F z)(F0) F s)=-R·g (Fu=0) sh(-Faz) (F.<0)》 F 1-C(,Fw) 222 D.(xF.)=(-F.)·2n+2 F (F.≠0) (Fu=0) 9
9

上述3个函数的命名与基本性质如下: Cw为“似余弦函数”,满足 C"+F.·Cw=0 C.(0)=1 Cw'(0)=0 S,为“似正弦函数”,满足 S"+F.·S4=0 S.(0)=0 S.'(0)=1 D为“色散发生函数”,满足 D"+F.·Dw=1 D(0)=0 D.'(0)=0 10
10

由此可见,这3个特殊函数都具有满足某一特定条件的最基 本单元的意味.考虑到复变函数论中三角函数和双曲三角函数的 关系及当~或F,趋于0时求极限,每个特殊函数尽管当F,取不 同值时有不同写法,或曰需用不同的计算方法求值,事实上各是一 个“统一”的函数,而且对F的变化都是连续的. 3个函数皆以之为第一自变量,F为第二自变量或参变量, 所以,如后面括号内只写一个自变量,就意味着它是之,而且“”代 表对之微分.Cm无量纲,S.与D.的单位分别是m和m(方程参 量Fu,G.的单位分别是m2和m1).容易看到,Cu与D是之的 偶函数,S是之的奇函数.它们还有以下性质: 基本恒等式: Cw2+Fk·Sw2=1 Cu+Fu·Du=1 Sn2=D.(1十Cm) 11
11