
第7章束流传输理论的主要问题 。7.1概述 ·7.2曲轴正交坐标系(自然坐标系)及磁 场、轨迹方程表达式 ·7.3多维相空间和传输矩阵 2
2 第7章 束流传输理论的主要问题 • 7.1 概述 • 7.2 曲轴正交坐标系(自然坐标系)及磁 场、轨迹方程表达式 • 7.3 多维相空间和传输矩阵
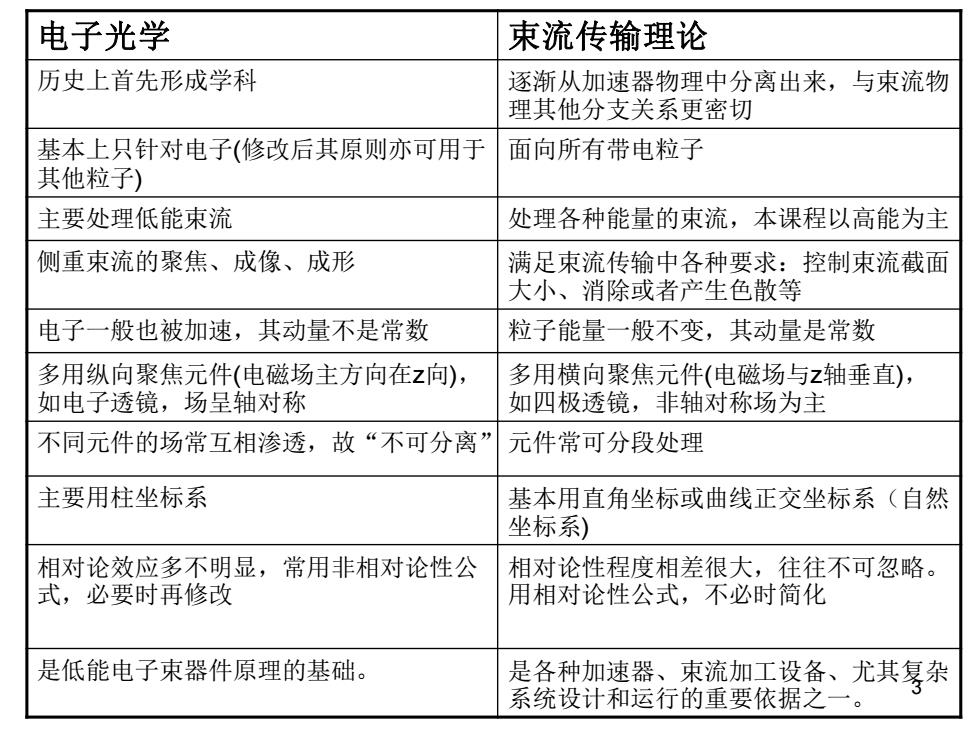
电子光学 束流传输理论 历史上首先形成学科 逐渐从加速器物理中分离出来,与束流物 理其他分支关系更密切 基本上只针对电子(修改后其原则亦可用于 面向所有带电粒子 其他粒子) 主要处理低能束流 处理各种能量的束流,本课程以高能为主 侧重束流的聚焦、成像、成形 满足束流传输中各种要求:控制束流截面 大小、消除或者产生色散等 电子一般也被加速,其动量不是常数 粒子能量一般不变,其动量是常数 多用纵向聚焦元件(电磁场主方向在z向), 多用横向聚焦元件(电磁场与z轴垂直), 如电子透镜,场呈轴对称 如四极透镜,非轴对称场为主 不同元件的场常互相渗透,故“不可分离” 元件常可分段处理 主要用柱坐标系 基本用直角坐标或曲线正交坐标系(自然 坐标系) 相对论效应多不明显,常用非相对论性公 相对论性程度相差很大,往往不可忽略。 式,必要时再修改 用相对论性公式,不必时简化 是低能电子束器件原理的基础。 是各种加速器、束流加工设备、尤其复杂 系统设计和运行的重要依据之一
3 电子光学 束流传输理论 历史上首先形成学科 逐渐从加速器物理中分离出来,与束流物 理其他分支关系更密切 基本上只针对电子(修改后其原则亦可用于 其他粒子) 面向所有带电粒子 主要处理低能束流 处理各种能量的束流,本课程以高能为主 侧重束流的聚焦、成像、成形 满足束流传输中各种要求:控制束流截面 大小、消除或者产生色散等 电子一般也被加速,其动量不是常数 粒子能量一般不变,其动量是常数 多用纵向聚焦元件(电磁场主方向在z向), 如电子透镜,场呈轴对称 多用横向聚焦元件(电磁场与z轴垂直), 如四极透镜,非轴对称场为主 不同元件的场常互相渗透,故“不可分离” 元件常可分段处理 主要用柱坐标系 基本用直角坐标或曲线正交坐标系(自然 坐标系) 相对论效应多不明显,常用非相对论性公 式,必要时再修改 相对论性程度相差很大,往往不可忽略。 用相对论性公式,不必时简化 是低能电子束器件原理的基础。 是各种加速器、束流加工设备、尤其复杂 系统设计和运行的重要依据之一

回顾电子光学 4
4 回顾电子光学

回顾电子光学 1.1轴对称电场和磁场 E.=-V+v-… E=2V,-wp+… B.(x)=B.()-4B"7+ B.()=-2Br+6B"r- 1.2电子在轴对称电场中的运动·高斯轨迹方程 F(')'+Vr=0 (P(z)x')'+Q(z)r=0 1.3电子在轴对称电磁场中的运动·布许定理 W('+子V+B)r=0 5 2m
5 回顾电子光学

1.4横向运动线性方程的解的矩阵形式 (P(x)·r)′+Q(z)·r=0 rc称为“似余弦解”,它满足运动方程c()=1r'()=0 称为“似正弦解”,它满足运动方程(a)=0'(之)=P) r(z)=r%·re(z)+Por′·rs(z) Px()=P(z)(r·re'(z)+Pm′·r'()) 传输矩阵 rc 元传输矩阵 1 , 6
6

1.5传输矩阵与相空间、发射度和包络·刘 维尔定理 mi m2 01 612 M- m21 m22 012 22 以状态点坐标(r,P,)为方程变量,(rm,P,m)为束流质心 用矩阵Σ的益处是它的矩阵元即o1,o2和o2与粒子群性质联系密切 (U一Um)T∑1(U一Um)≤1πe就是该椭圆的面积e= /No1122- 2 012 或22(r-rm)2-2o2(r-rm)(P,-P,m)十1(P,-Pm)2≤e 011 n,3 2m1m12 m2 Um(动=MUm(a) 012 m121 1+2m42m1 m12n22 612 ←> Σ(=M()(M)I 022) 2 m21 m22 2 m22 022 3= 01 1 ,Q ,Y=型令R=Vo1为束流包络 7 刘维尔定理 相空间粒子集合体积在传输中不变
7
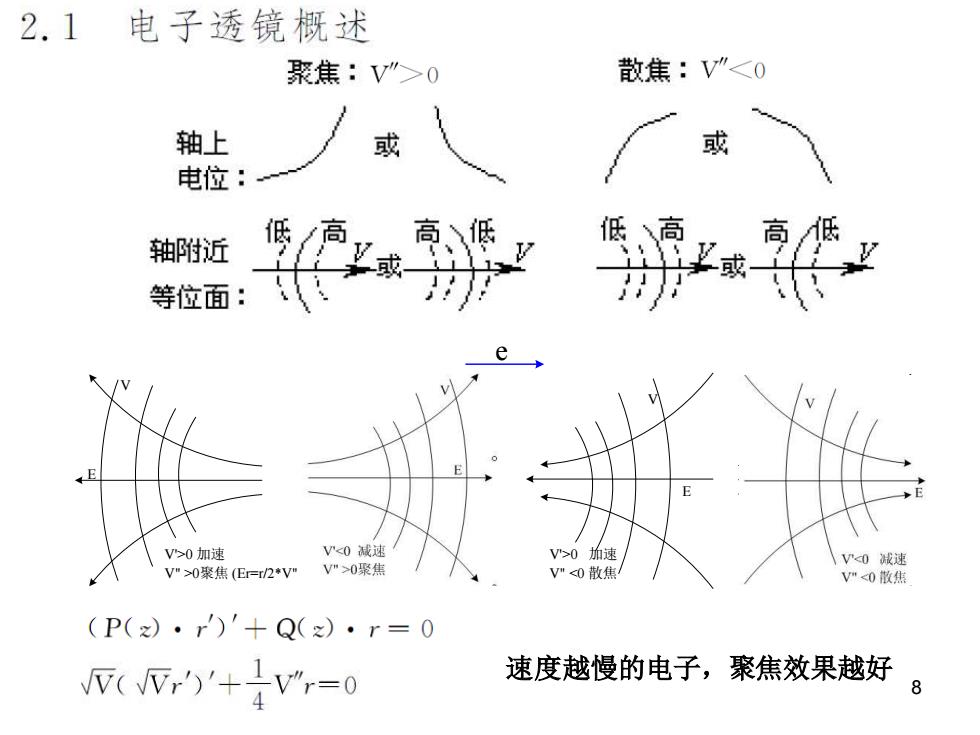
2.1 电子透镜概述 聚焦:V">0 散焦:V”0加速 V0加速 V0减速 V">0聚焦(E=r/2*V" V">0聚焦 V"<0散焦 V”0散焦 (P(z)·r)'+Q(x)·r=0 ()'+子=0 速度越慢的电子,聚焦效果越好
8 E V e V'>0 加速 V" >0聚焦 (Er=r/2*V") E V V'0聚焦 E V V'0 加速 V" <0 散焦 E V 速度越慢的电子,聚焦效果越好
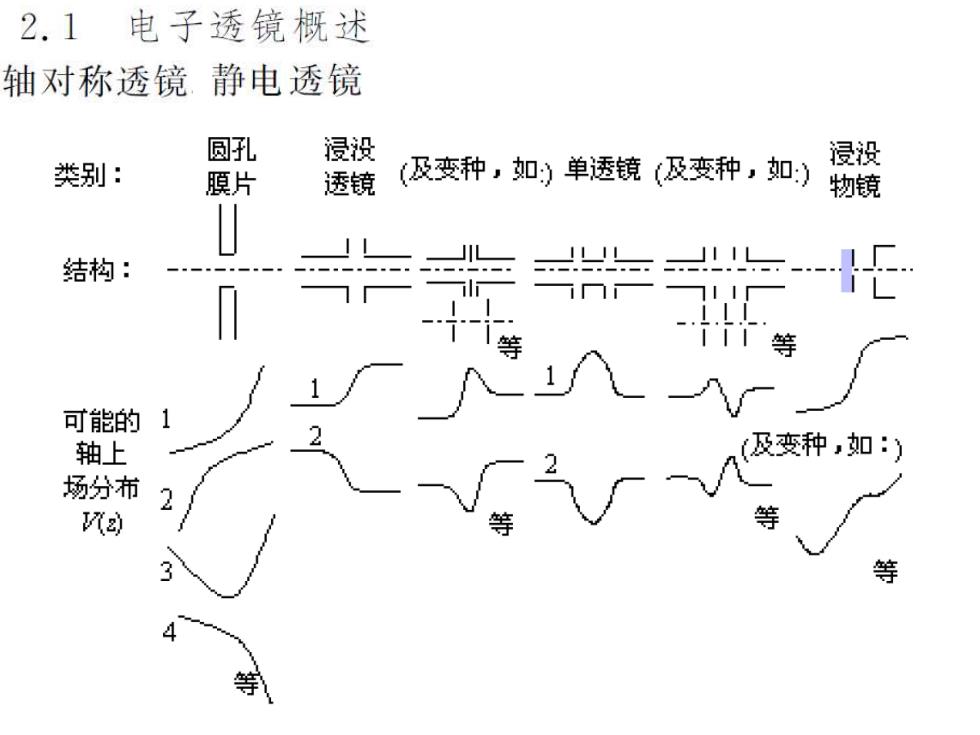
2.1电子透镜概述 轴对称透镜静电透镜 圆孔 浸没 类别: 膘片 透镜 (及变种,如)单透镜(及变种,如) 浸没 物镜 结构: 可能的 轴上 (及变种,如: 场分布 等 等 等
9
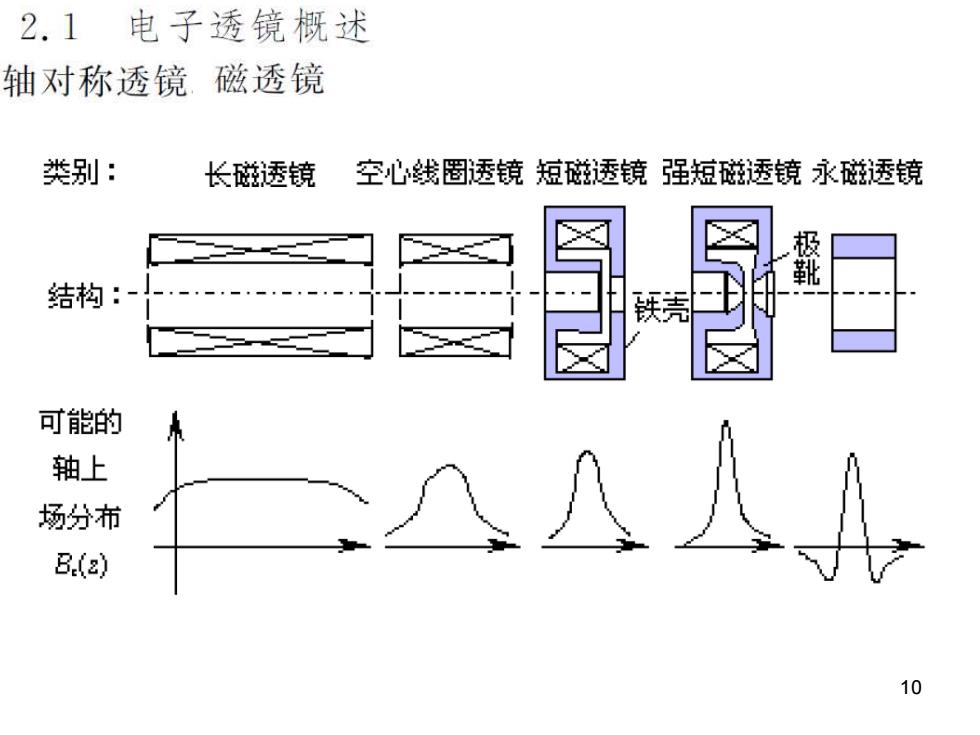
2.1 电子透镜概述 轴对称透镜磁透镜 类别: 长磁透镜 空心线圈透镜短磁透镜强短磁透镜永磁透镜 极 靴 结构: 可能的 轴上 场分布 B.( 10
10

2.2电子透镜的主要参量和传输矩阵、场分布 (P()·r)'+Q(z)·r=0 径向轨迹方程 ()'+V"+2Br=0 2m mii m2 薄透镜 厚透镜 m21 m22 m1= Qd之物方、像方焦距分别为f。=P。f,f=Pf 在电子光学中,对于静电透镜(B.=0),则有 六≈长:i=wf=W “简正焦距”F 在静电透镜中定义网数(R=V,F=Y 而对于磁透镜(设V=常数),则有 ≈Q=8 B.2dz 11 然后根据轴对称透镜的电磁场分布求的其焦距
11 然后根据轴对称透镜的电磁场分布求的其焦距