
1电子在轴对称场中的运动 。1.1轴对称电场和磁场 ·1.2电子在轴对称电场中的运动(高斯轨迹方程) ·1.3电子在轴对称电磁场中的运动(布许定理) ·1.4横向运动线性方程的解的矩阵形式 ·1.5传输矩阵与相空间、发射度和包络(刘维尔定理) 2
2 1 电子在轴对称场中的运动 • 1.1 轴对称电场和磁场 • 1.2 电子在轴对称电场中的运动(高斯轨迹方程) • 1.3 电子在轴对称电磁场中的运动(布许定理) • 1.4 横向运动线性方程的解的矩阵形式 • 1.5 传输矩阵与相空间、发射度和包络(刘维尔定理)
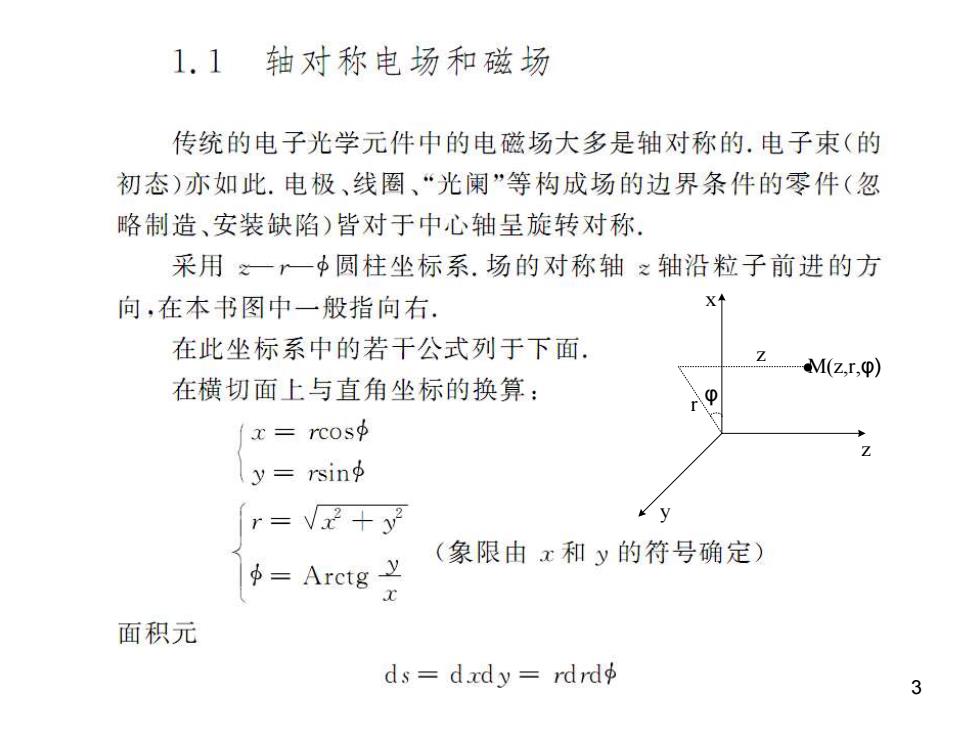
1.1轴对称电场和磁场 传统的电子光学元件中的电磁场大多是轴对称的.电子束(的 初态)亦如此.电极、线圈、“光阑”等构成场的边界条件的零件(忽 略制造、安装缺陷)皆对于中心轴呈旋转对称. 采用x一一中圆柱坐标系.场的对称轴之轴沿粒子前进的方 向,在本书图中一般指向右 X 在此坐标系中的若干公式列于下面. Z M(z,r,) 在横切面上与直角坐标的换算: x=rcosp y=rsin中 r=Vx十y (象限由x和y的符号确定) =Aretg y x 面积元 ds=dxdy=rdrdφ 3
3 M(z,r,φ) r φ z z x y

哈密顿算子V在直角坐标中的表示式为:7= 据上述坐标变量之间的微分关系为: a ay ⑦水 层+保°+层-(是-品+异+多+保 -(}++ 哈密顿算子7在柱坐标中的表示式为:了=寻。 +e+ 标志梯度、散度、旋度等的耐普拉算子: A=++e ar r∂φ 7·A=1(A)+1A+ aA r∂r r∂中 az V X A=e, (1 aA. (OA,aA: ia ra中 az) ar 8 x z 十e. 1 ∂(A)aA ar ao V2A= a∂A 1 4 r∂r'∂r 02 又2一拉普拉斯算子
4
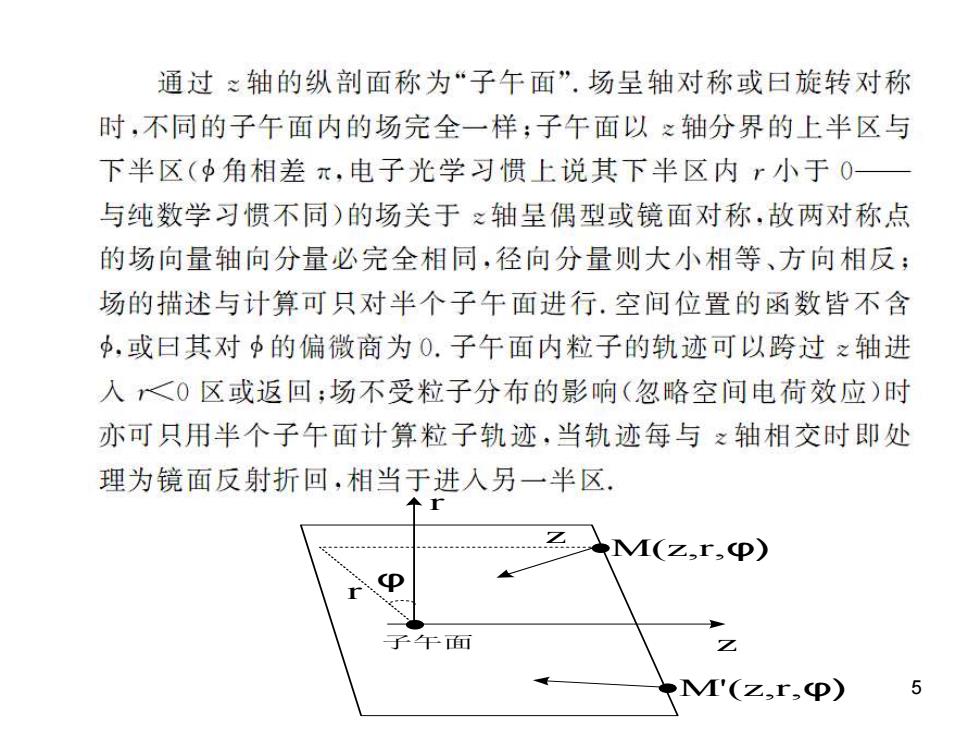
通过≈轴的纵剖面称为“子午面”.场呈轴对称或日旋转对称 时,不同的子午面内的场完全一样;子午面以之轴分界的上半区与 下半区(角相差π,电子光学习惯上说其下半区内x小于0一 与纯数学习惯不同)的场关于之轴呈偶型或镜面对称,故两对称点 的场向量轴向分量必完全相同,径向分量则大小相等、方向相反; 场的描述与计算可只对半个子午面进行.空间位置的函数皆不含 中,或日其对中的偏微商为0.子午面内粒子的轨迹可以跨过之轴进 人<0区或返回:场不受粒子分布的影响(忽略空间电荷效应)时 亦可只用半个子午面计算粒子轨迹,当轨迹每与之轴相交时即处 理为镜面反射折回,相当于进入另一半区. M(z,r,φ) 子面 '(z,r,p) 5
5 M(z,r,φ) r φ z z r 子午面 M'(z,r,φ)

空间电磁场非可任意选取.它们必须: (1)(目前看来,绝对地)服从麦克斯韦方程; (2)(如果是理想场,则)满足某些特定条件,如本章的轴 对称: (3)(可能是近似地)符合某些数学处理所要求的其他条件 麦克斯韦方程和电荷连续性方程如下: 7·D=p 7XE=一 aB D=E ∂t 7·B=0 及 V X H- aD十J B=uH at 7·J+ 3p二0 at 6
6

在束流光学中,束流一般在高真空环境中,故式中介电常数€ 和磁导率可用真空中的ε。和h代替,而场向量D和H可分别 以E和B取代;不考虑空间电荷效应时,可忽略空间电荷密度P 和空间电流密度J(考虑时,勿忘电子电荷带来的负号):绝大多数 情况下,电磁场为静态或似稳态(随时间变化甚慢),故各量对t的 偏微商可取为0. V.E= 7·E=0 E0 7·B=0 7·B=0 VxE=-a1 V×E=0 ∂E V×B=0J+o0at 7×B=0 所以,本章(大多数情况下全书亦然)认为电场强度E和磁场 强度B都是散度、旋度皆为0的向量场
7

E作为无旋场,可用静电位场V描述,E=一V. B作为无源场,可用向量势场A(附加条件:A无源,即7·A =0)描述,B=7×A.当B亦无旋时,也可形式地用标量磁位Vm 描述.本书一般直接用B,而不用Vm或A,也很少用到场向量H. 因为作者以为,B能通过洛伦兹力作用于带电粒子、与场的空间储 能相联系、可以直接测量,所以唯它有资格“真实”地在物理意义上 代表磁场(一如E之于电场),“磁场强度”之名亦只有它可当之无 愧,而其他量在某种程度上只具有数学意义 既然皆是无旋无源的轴对称场,本章中E和B在近轴区域满 足同样的偏微分方程,其定性特征相似,但与边界条件的关系和生 成的方式迥然不同. 8
8
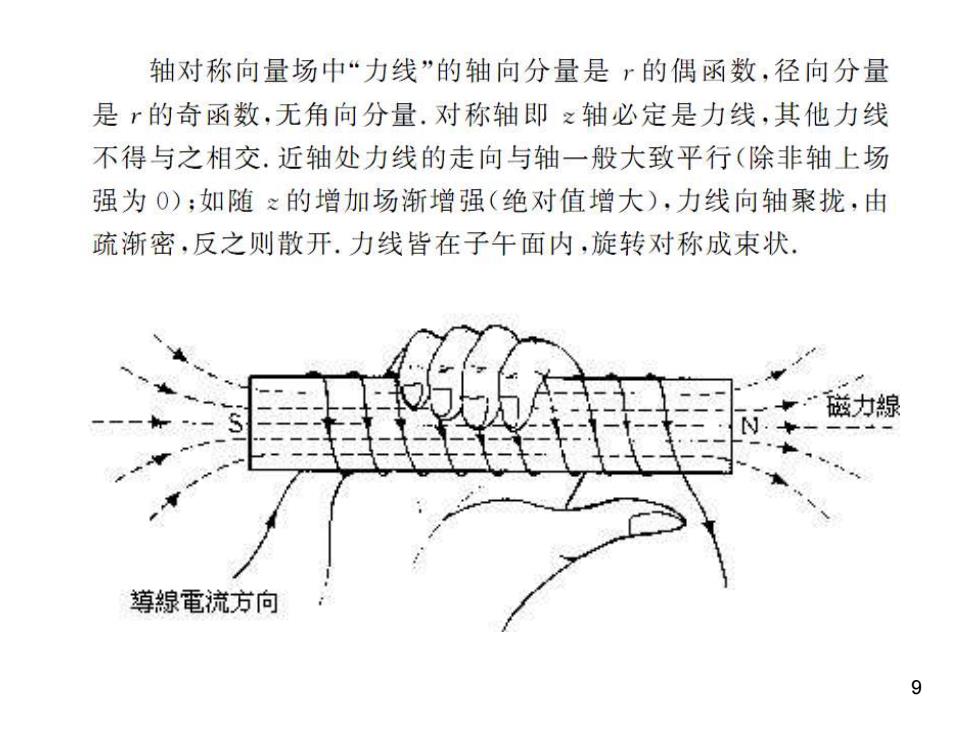
轴对称向量场中“力线”的轴向分量是r的偶函数,径向分量 是r的奇函数,无角向分量.对称轴即之轴必定是力线,其他力线 不得与之相交.近轴处力线的走向与轴一般大致平行(除非轴上场 强为O);如随~的增加场渐增强(绝对值增大),力线向轴聚拢,由 疏渐密,反之则散开.力线皆在子午面内,旋转对称成束状 磁力線 導線電流方向 9
9

轴对称场的位V也必是r的偶函数.V的分布可用等位面描 述,力线E是其法线.所有等位面皆为绕z轴的旋转曲面,其与子 午面的交线在近轴处近似为关于之轴对称的二次曲线,与之轴正 交(除非该点V取极值,故E=0,且易号),呈或凸或凹的弧形或 近于平行直线.以等差的多层等位面描述V,E强处其相聚紧密, 弱处则稀疏.与力线的特性综合,随~的增加,如E大致不变,则 等位面大体是等距平面,力线近乎平行;若E渐增强,则等位面渐 向左凹回,间距变小,力线会聚:若E渐减弱,则等位面渐向右凸 前,间距放宽,力线发散, 等位面V r等位面V 电场E e e 轴上电位 高电位 低电位 VO(聚焦) 电场正 10 类似,光学中的凸透镜,光子进入凸透镜减速并聚焦,折射率越大,聚焦越强
10 等位面V r r z 电场E 等位面V e e e 电场E 高电位 低电位 轴上电位 V'0(聚焦) 类似,光学中的凸透镜,光子进入凸透镜减速并聚焦,折射率n越大,聚焦越强
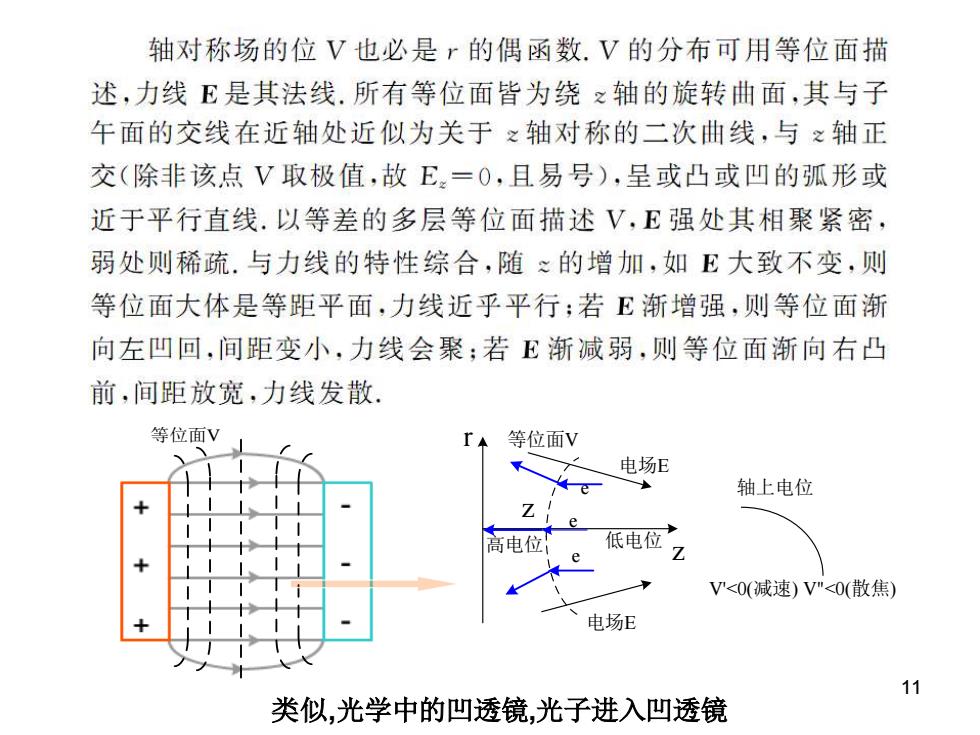
轴对称场的位V也必是r的偶函数.V的分布可用等位面描 述,力线E是其法线.所有等位面皆为绕之轴的旋转曲面,其与子 午面的交线在近轴处近似为关于之轴对称的二次曲线,与之轴正 交(除非该点V取极值,故E,=0,且易号),呈或凸或凹的弧形或 近于平行直线.以等差的多层等位面描述V,E强处其相聚紧密, 弱处则稀疏.与力线的特性综合,随≈的增加,如E大致不变,则 等位面大体是等距平面,力线近乎平行;若E渐增强,则等位面渐 向左凹回,间距变小,力线会聚;若E渐减弱,则等位面渐向右凸 前,间距放宽,力线发散 等位面V r等位面V 电场E e 轴上电位 Z e 高电位 低电位 Z V<0(减速)V"<O(散焦) 电场E 11 类似,光学中的凹透镜,光子进入凹透镜
11 等 位 面 V 类似 ,光学中的凹透镜 ,光子进入凹透镜 z z r 电 场 E 等 位 面 V e ee 电 场 E 高 电 位 低 电 位 轴 上 电 位 V ' < 0 ( 减 速 ) V " < 0 ( 散 焦 )