
The Sixth Overseas Chinese Physics Association ACCELERATOR SCHOOL Beijing,China,July 29 Augusr 72010 束流传输和束流操纵 (Beam Transport and Manipulation) 中国科学院高能物理研究所 唐靖宇 0CPA2010,北京,J1.YTag
束流传输和束流操纵 (Beam Transport and Manipulation) Beam Transport and Manipulation) 中国科学院高能物理研究所 唐靖宇 OCPA 2010, 北京, J. Y. Tang

主要内容 了引言 了束流光学的基本理论 了输运线线性光学设计的一般方法 了横向相空间的匹配 了纵向相空间的匹配 了束流的多路分束 了束晕刮除和动量分析 了 束流分布变换 CSNS输运线设计的例子 0CPA2010,北京,J.Y.Tang
主要内容 引言 束流光学的基本理论 输运线线性光学设计的一般方法 横向相空间的匹配 纵向相空间的匹配 束流的多路分束 束晕刮除和动量分析 束流分布变换 CSNS输运线设计的例子 OCPA 2010, 北京, J. Y. Tang

§1引言 束流传输 ●大型加速器的不同加速段之间通常需要束流输运线进行连 接,将从加速器引出的束流传送到各实验终端或靶站也需 要通过束流传输系统和束流分配系统来进行。 ●通常束流输运线的光学设计较环形加速器要简单一些,主 要是因为束流只是一次性通过(线性光学设计) ●没有束流加速问题 ·相空间匹配问题:横向相空间和纵向相空间中的匹配 ●空间位置安排相对来说也较环中的要轻松一些 束流操纵 ·束流至不同的后级加速器或实验站的分束 ●束晕的刮除 ·束流分布变换 ●电荷态分析和选择(特别是重离子束) 0CPA2010,北京,J.YTag
§1 引言 束流传输 大型加速器的不同加速段之间通常需要束流输运线进行连 接,将从加速器引出的束流传送到各实验终端或靶站也需 要通过束流传输系统和束流分配系统来进行。 通常束流输运线的光学设计较环形加速器要简单 通常束流输运线的光学设计较环形加速器要简单 些一 ,主 要是因为束流只是一次性通过(线性光学设计) 没有束流加速问题 相空间匹配问题:横向相空间和纵向相空间中的匹配 空间位置安排相对来说也较环中的要轻松一些 束流操纵 束流至不同的后级加速器或实验站的分束 束晕的刮除 束流分布变换 电荷态分析和选择(特别是重离子束) OCPA 2010, 北京, J. Y. Tang 电荷态分析和选择(特别是重离子束)

§2束流光学的基本理论 束流光学与束流动力学 。束流光学(beam optics):通常是处理加速器中的束流传输 段和电子显微镜(电子光学)中束流的运动规律,一般不 处理加速问题和多次循环问题,一般也不处理高阶场不稳 定性问题和束流集体不稳定性问题;采用与几何光学类似 的方法即线性矩阵方法的描述为主,配合一些色差和像差 的校正。 ●束流动力学(beam dynamics):通常是处理加速器中束流的 运动,包括加速过程、各种高阶场不稳定性和集体不稳定 性。在不考虑空间电荷效应和集体不稳定性的情况下,以 采用单粒子的跟踪方法为主。 ●二者之间是有交叉的,基本原理也是相近的。 束流光学的研究方法 ●描迹法 ●传输矩阵法 0CPA2010,北京,J1.YTag
§2 束流光学的基本理论 束流光学与束流动力学 束流光学(beam optics):通常是处理加速器中的束流传输 段和电子显微镜 段和电子显微镜(电子光学)中束流的运动规律 中束流的运动规律,一般不 处理加速问题和多次循环问题,一般也不处理高阶场不稳 定性问题和束流集体不稳定性问题;采用与几何光学类似 的方法即线性矩阵方法的描述为主,配合一些色差和像差 的校正。 束流动力学(beam dynamics):通常是处理加速器中束流的 运动,包括加速过程、各种高阶场不稳定性和集体不稳定 性。在不考虑空间电荷效应和集体不稳定性的情况下,以 采用单粒子的跟踪方法为主。 二者之间是有交叉的,基本原理也是相近的。 束流光学的研究方法 描迹法 OCPA 2010, 北京, J. Y. Tang 传输矩阵法
束流发射度、C-S不变量和刘 维定理 ●束流发射度: ·在相空间中包含一定粒子数比例 的相椭圆面积(π)。 [rms,95%,100%] 。椭圆方程: a.(22 6,(22)x2-26,12)x'+6,110x2=8 7 。束流矩阵的表示 01 a.-0.0wo.m 0,(11)0.12) (】 1o,1 V(22 ●刘维定理[横向运动中已有介绍] ·束流发射度在由电场和磁场组成 的加速器中运动时通常保持不变。 0CpA2010,北京,J.YTag
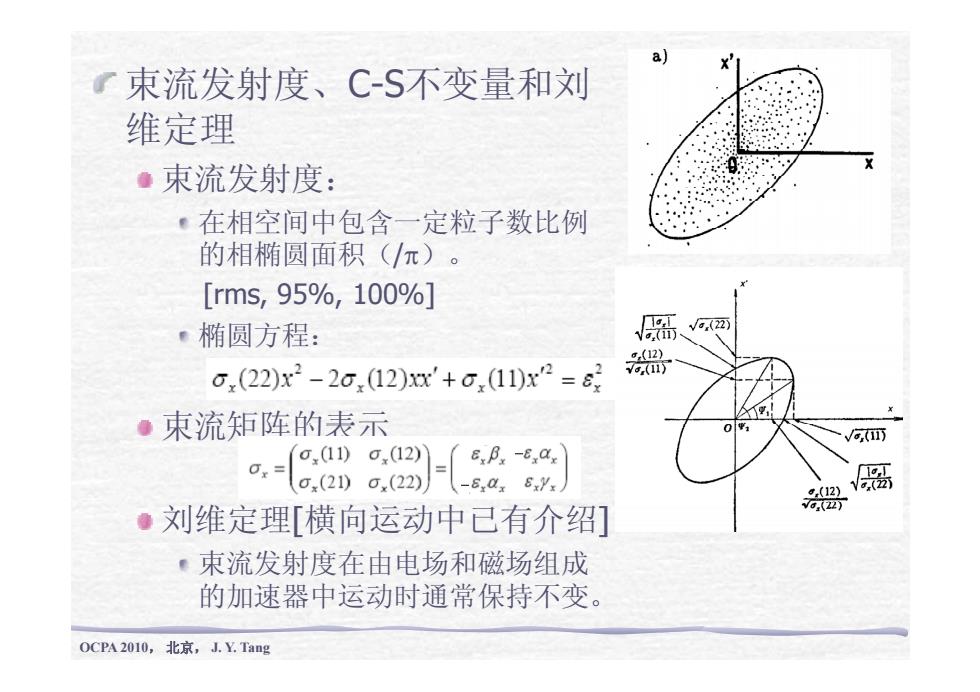
束流发射度、C-S不变量和刘 维定理 束流发射度: 在相空间中包含一定粒子数比例 的相椭圆面积(/π)。 [rms, 95%, 100%] 椭圆方程: 束流矩阵的表示 刘维定理[横向运动中已有介绍] 束流发射度在由电场和磁场组成 OCPA 2010, 北京, J. Y. Tang 的加速器中运动时通常保持不变

。C-S不变量 代表单个粒子的振荡能量,通常也是运动中不变的。 Yx2+2axx+Bx=(6)=21 1=(1+2a2)6,ms 了束流光学的描述方法 X 。描迹法:跟踪单个粒子的运动 x' x' ·传输矩阵法:将束流作为一个整体来 考虑 y ●6维相空间: y' =M y 每个粒子除初始条件外是相同的,6N △1 维相空间简并为6维相空间。 p MP 3个投影相平面(xx,y-y°,中-△p/p)。 0CpA2010,北京,J1.YTag
C-S不变量 代表单个粒子的振荡能量,通常也是运动中不变的。 x x x x x x 2 xx x ( ) 2I 2 2 γ + α ′ + β ′ = ε = I (1 2 )2 ⎛ x ⎞ ⎛ x ⎞ rms I (1 2α )ε 2 = + 束流光学的描述方法 y x x y x x ⎟⎟⎟⎞ ⎜⎜⎜⎛ ′ ⎟⎟⎟⎞ ⎜⎜⎜⎛ ′ 描迹法:跟踪单个粒子的运动 传输矩阵法:将束流作为一个整体来 考虑 l y y M l y y ⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜ Δ′ = ⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜ Δ′ 考虑6维相空间: 每个粒子除初始条件外是相同的 6N f i p p l p p l ⎟⎟⎟⎟⎠ ⎜⎜⎜⎜⎝ ΔΔ ⎟⎟⎟⎟⎠ ⎜⎜⎜⎜⎝ Δ 每个粒子除初始条件外是相同的,6N Δ 维相空间简并为6维相空间。 3个投影相平面 (x-x’, y-y’, φ-Δp/p)。 OCPA 2010, 北京, J. Y. Tang 3个投影相平面 (x x , y y , φ Δp/p)。 f i
1L000 0 0 01000 常见束流传输元件的传 001L0 0 M= 000100 输矩阵 00001L1/y2 ·自由漂移空间:L 000001 ·磁四极透镜 coskL 咖红 0 0 0 0 =马1 -k sin kL coskL 0 000 1 a Bp Mo= 0 0 coshkL sinh kL 00 0 0 k sinh kL coshkL 00 ·偏转磁铁 0 0 0- 01L1y2 0 0 0 001 h=1/p,k=(1-n)h2,号=nh2 cosk,L 在sn长红 0 0 0 (-cosk,) h -k,sin k L cosk,L 0 00 h 磁铁本体 咖长L Mo= 0 0 coskL mL0 1 0 部分 0 0 -k,sin k,L cosk,L 0 0 0 咖L h (1-cosk,L) 01 2 0 0 0 0 0 0CPA2010,北京,J.YTag
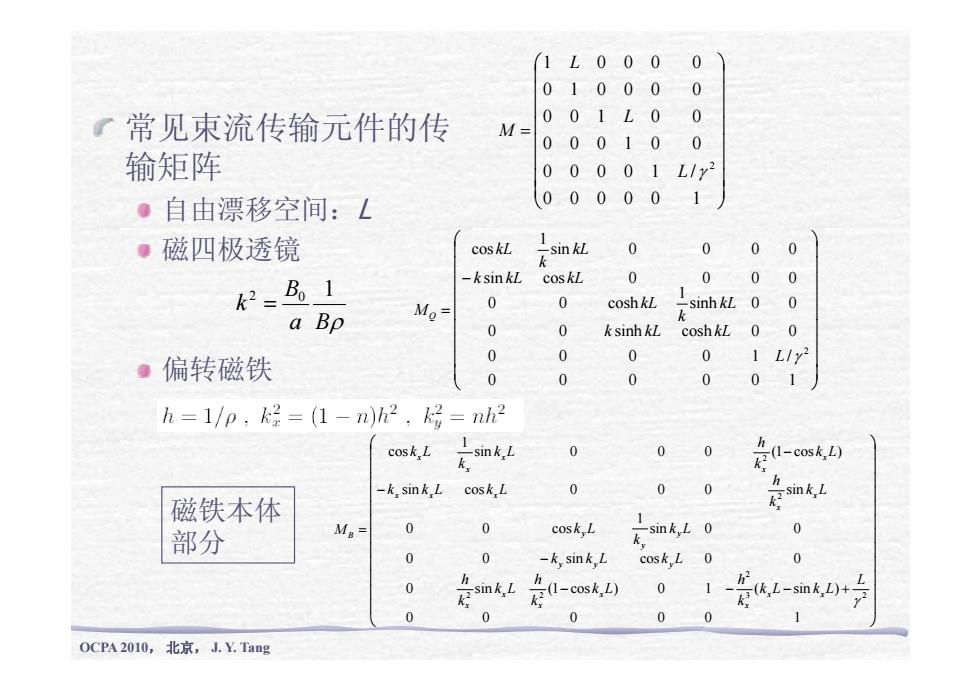
⎟ ⎟ ⎟ ⎞ ⎜ ⎜ ⎜ ⎛ 0 0 1 0 0 0 1 0 0 0 0 1 0 0 0 0 L L 常见束流传输元件的传 输矩阵 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ = 0 0 0 0 1 / 0 0 0 1 0 0 0 0 1 0 0 2 L γ L M 自由漂移空间: L 磁四极透镜 ⎟ ⎠ ⎜ ⎝ 0 0 0 0 0 1 ⎟ ⎟ ⎞ ⎜ ⎜ ⎛ sin 0 0 0 0 1 cos kL k kL ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ − = 0 0 sinh cosh 0 0 sinh 0 0 1 0 0 cosh sin cos 0 0 0 0 k kL kL kL k kL k kL kL k M Q a Bρ B k 2 0 1 = 偏转磁铁 ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ 0 0 0 0 0 1 0 0 0 0 1 / 2 L γ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ − − sin cos 0 0 0 sin sin 0 0 0 (1 cos ) 1 cos 2 2 k L k h k k L k L k L k h k L k k L x x x x x x x x x 磁铁本体 ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ − = 0 0 sin cos 0 0 sin 0 0 1 0 0 cos 2 h h h L k k L k L k L k k L k M y y y y y y x B 磁铁本体 部分 OCPA 2010, 北京, J. Y. Tang ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎝ − − − + 0 0 0 0 0 1 0 sin (1 cos ) 0 1 ( sin ) 2 2 3 2 γ L k L k L k h k L k h k L k h x x x x x x x
●偏转磁铁的边缘角 心= 1+in2 cos B 1 0 0 000 tanB 1 0 000 p 00 1 000 M Rot= 0 0 tan(B-y) 100 0 0 0 010 00 0 001 0CPA2010,北京,1.YTag
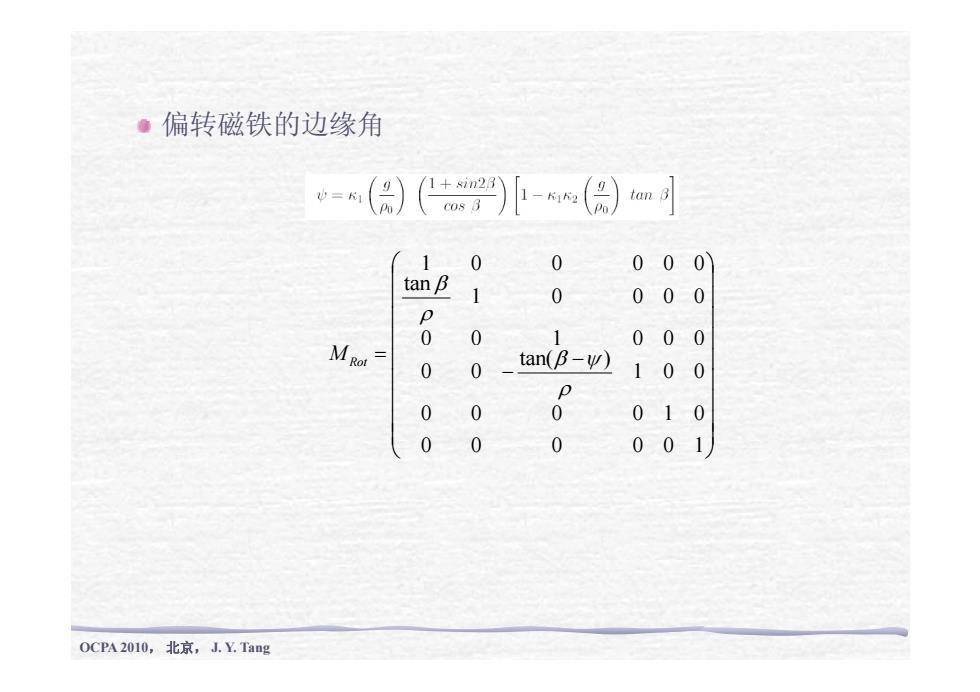
偏转磁铁的边缘角 ⎟⎞ ⎜⎛ 1 0 0 0 0 0 ⎟⎟⎟⎟⎞ ⎜⎜⎜⎜⎛ 0 0 1 0 0 0 1 0 0 0 0 tan1 0 0 0 0 0 ρβ ⎟⎟⎟⎟⎟⎟ ⎜⎜⎜⎜⎜⎜ − − = 0 0 0 0 1 0 1 0 0 tan( ) 0 0 ρ MRot β ψ ⎟⎟⎠ ⎜⎜⎝ 0 0 0 0 0 1 OCPA 2010, 北京, J. Y. Tang

束流传输的一般表示 装配矩阵 ●一系列传输元件的总作用 R R12 R RIs R16 矩阵(装配矩阵)是单个 R21 R22 R23 RA R25 R26 元件传输矩阵的乘积(有 R= R31 R32 R33 R34 R35R6 时也称为R矩阵): Ra R32 R43 Ri Ras R46 R52 R56 M=Mn…M2M1 束流矩阵的变换 O:=M.O0MI =MooM 0CpA2010,北京,J.YTag
束流传输的一般表示 装配矩阵 一系列传输元件的总作用 ⎟ ⎟ ⎞ ⎜ ⎜ ⎛ 11 12 13 14 15 16 R R R R R R R R R R R R 矩阵(装配矩阵)是单个 元件传输矩阵的乘积(有 时也称为 R矩阵 ) ⎟ ⎟ ⎟ ⎟ ⎜ ⎜ ⎜ ⎜ = 31 32 33 34 35 36 21 22 23 24 25 26 R R R R R R R R R R R R R R R R R R R 时也称为 R矩阵 ): M = M n L M 2 M1 ⎟ ⎟ ⎟ ⎟ ⎠ ⎜ ⎜ ⎜ ⎜ ⎝ 51 52 53 54 55 56 41 42 43 44 45 46 R R R R R R R R R R R R R R R R R R 束流矩阵的变换 n 2 1 ⎝ R61 R62 R63 R64 R65 R66 ⎠ T σ x = M x σ x 0 M x T σ = Mσ 0 M OCPA 2010, 北京, J. Y. Tang

了六维束流矩阵的表示 σ矩阵具有关于对角线的对称性 ●r矩阵又称为是关联矩阵(beam matrix correlations) T' a' 011 V011 MM 021 02 V022 MR T21 031 032 033 y V033 MM T31T32 041 042 043044 Vo4 MR T41 T42 T43 T51 052 053054055 V055 MM T61 T52T53T54 061 062063064065 066 V066 PM T61T62 T63T64T65 0i词 ”120代表相椭圆是发散的 T21=T12= V1+a7 √丙 0CPA2010,北京,1.Y.Tag
六维束流矩阵的表示 σ矩阵具有关于对角线的对称性 r矩阵又称为是关联矩阵(beam matrix correlations) Î r120代表相椭圆是发散的. OCPA 2010, 北京, J. Y. Tang