
第九章组合系统设计 。9.1概述 ·9.2消色散系统 ·9.3发射度匹配和组合系统设计计算
第九章 组合系统设计 • 9.1 概述 • 9.2 消色散系统 • 9.3 发射度匹配和组合系统设计计算

单个粒子的“完整”的轨迹为 回顾 x=+(-+a.6os盘+ η与传输矩阵的关系为 m12 mis m21 22 m26 此关系既可用于已知初值和所有传输矩阵元求()和)(), 也可用于已知)与)'的初值、终值和其他矩阵元反算矩阵元m6 和m2s. 由传输矩阵元求3等函数 m2 -2m1m2 n22 n1m21 2m4221+1 222 a n12 -221me2 2 n22 Y o
回顾

9.1 概 述 组合系统是指由若干束流传输元器件组成的具有一定功能的 束流传输系统,这些元器件一般包括弯转磁铁、四极磁铁和漂移 段.设计的目的总是尽量使该系统具有所要求的功能,不必要的束 流损失尽量少,而又尽量简单、经济、便于操作.“简洁为美”应视为 设计的一个原则.系统的特色应来自设计目标的特殊要求、外部客 观条件(如束流源、使用环境、空间位置等)的局限和综合考虑各种 要求与利弊的折衷优化.代价高昂的复杂化应该是“必须”的,仅仅 “有所改善”不是充足的理由, 对束流传输系统的第一个要求往往涉及理想轨道的几何布局 与匹配.理想轨道一般由直线段和弯转平面内的转角为O的圆弧 段构成. 弯转磁铁 漂移段
θB ρ 漂移段 弯转磁铁

一般而言,传输系统的起点、终点和进行束流测量的地点都在 漂移段.本节先对漂移段内的束流性质稍作更深入的讨论,然后引 入接受度的概念 漂移段内F=0,G=0.)=n'和Y=Ym是常数.束流的 7=0十门'(之-) B.=30-2au(之-)+Ya(x-x)2 a=Q0一Y0(之一z) 漂移段的传输矩阵 -6 -2m1m12 m 1 -2L 2 -m11m21 22m21+1-m12m2 do 0 1 -L a m -2m21m22 m 0 0 1 Yo 7 m m2 m6 L m21 m22 1 76
0 0 1 0 1 u L u u u = 漂移段的传输矩阵 2 2 2 11 11 12 12 0 0 11 21 12 21 12 22 0 0 2 2 21 21 22 22 0 0 2 1 2 2 1 0 1 2 0 0 1 m m m m L L m m m m m m L m m m m − − = − + − = − − 11 12 0 16 0 21 22 0 26 0 1 0 1 m m m L m m m = + =
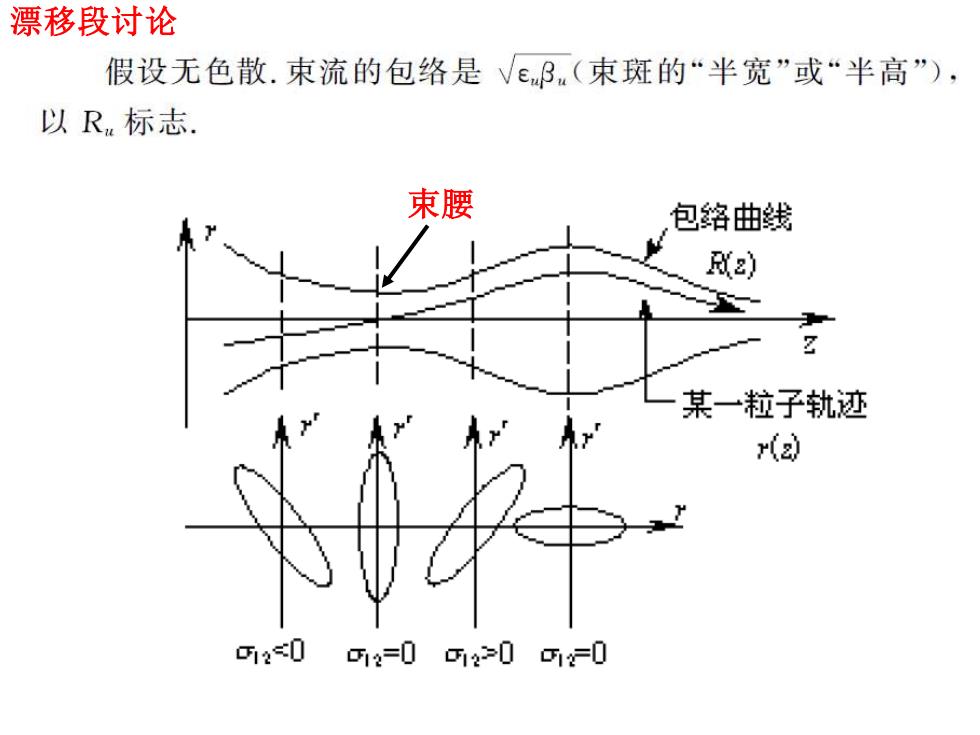
漂移段讨论 假设无色散.束流的包络是Ve3(束斑的“半宽”或“半高”), 以R标志 束腰 包络曲线 某一粒子轨迹 r 听20 12=0所12201F0
束腰 漂移段讨论

漂移段讨论 问题: (1)以下标w表示“束腰”.给出B,R依赖于腰点位置之w和 R的关系 β.=30-2ao(之-0)+Yo(之-0)2 au=a0一Y0(之一z0) 问题的答案是: (1)腰点处aw=0,Yw= 所以 1 B.=R? =R十}(之-)月 Eu 而 1 3曲线是以腰点为顶点的抛物线.B不仅本身是β的最小 值,而且由它决定偏离腰点后3.如何上升.B越小,上升越快
漂移段讨论
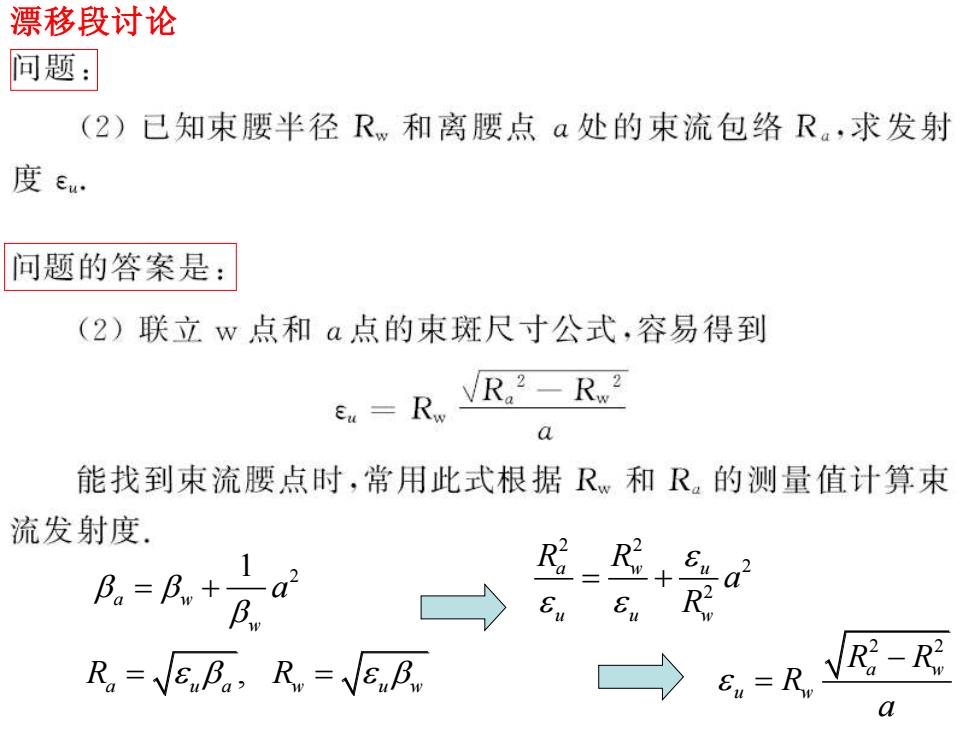
漂移段讨论 问题: (2)已知束腰半径Rw和离腰点a处的束流包络R。,求发射 度eu 问题的答案是: (2)联立w点和a点的束斑尺寸公式,容易得到 E-R Ra2-Rw2 a 能找到束流腰点时,常用此式根据R。和R。的测量值计算束 流发射度 B。=B。+ Eu R2 Rn=VEnf。,R。=VEnB。 Eu=R VR-R2
漂移段讨论 1 2 a w w a = + , R R a u a w u w = = 2 2 2 2 a w u u u w R R a R = + 2 2 a w u w R R R a − =

漂移段讨论 问题: (3)一般情况下,测量几处的束斑尺寸可间接计算e? 问题的答案是: 三点测量法,分别测量漂移段三点的束流包络R、R2、R3,求出发射度 R2=6wB=6u(B-2031+Yo2) 其中y 1+06 R=6nB2=6n(B。-2a22+Y22) R=6nB=6(B。-20o3+o23) 上面方程组,共三个未知数eu、α。、Bo,解方程组可得: 2√s(s-a)(s-a)(s-a3) (22-)(3-22)(3-月 其中:( 4=33-2R,4=3-1R,4=32-2R s=2(a+a+a)
漂移段讨论 三点测量法,分别测量漂移段三点的束流包络R1、 R2、 R3,求出发射度 ( ) ( ) ( ) 2 2 1 1 0 0 1 0 1 2 2 2 2 0 0 2 0 2 2 2 3 3 0 0 3 0 3 2 2 2 u u u u u u R z z R z z R z z = = − + = = − + = = − + 2 0 0 0 1 + 其中 = 上面方程组,共三个未知数εu、α0 、 β0,解方程组可得: ( )( )( ) ( )( )( ) 1 2 3 2 1 3 2 3 1 2 u s s a s a s a z z z z z z − − − = − − − 1 3 2 1 2 3 1 2 3 2 1 3 a z z R a z z R a z z R = − = − = − , , ( 1 2 3 ) 1 2 s a a a = + + 其中:

漂移段讨论 问题:(4)假设聚焦透镜出口为点,该处B=B,什么条件下可使 腰点最远? 3.=β0-2ao(之-0)十Yo(x-0)2 问题的答案是: au=a0一Y0(之一z0) (4)腰点处am=0,所以到腰点的距离 之一= Yo >0时会聚,腰点在前方.=1时腰点最远,在前方号处. 此时,漂移段中%= 所以腰点=R=号R。 在前方十3处的束流包络与在处一样. 所以,长漂移段前的四极透镜出口应使3不太小,大约为 1,方可使漂移段较长,或者说用的聚焦元件较少.太小或太大 意味着聚焦不足或过分
漂移段讨论

漂移段讨论 问题: (5)一漂移段长L,什么条件下全段中包络的极大值最小? 问题的答案是: (⑤5)当该段中点为束流腰点而且R。=L时,全段上尽=L (在两端)为最小. 此问题亦可理解为前一问题的另一种提法,因为此时两端点 处am=士1
漂移段讨论