
实验5气垫法测定物体的转动惯量 在很多情况下,物体的形状和大小对物体的运动规律起着重要作用,例如宏观物体的 转动,以及微观粒子如分子、原子的转动甚至电子的自转等等。在这种情况下,物体就不 能再被当作质点看待,而必须考虑物体的大小和形状,即把物体视为刚体。 在研究刚体的转动问题时,首先遇到的困难就是磨擦力矩的存在:本仪器由于采用了 气垫悬浮与气垫滑轮相结合以及气流定轴等独特设计,故该装置所有转动件间的磨擦均达 到可以忽略的程度。用它可以测量多种物体的转动惯量,能够完成转动定律、角动量守恒 定律及平行轴定理等许多实验。本实验利用气垫转动惯量测定仪测定刚体在力矩作用下转 动的角加速度,来验证刚体转动定律。 实验目的和学习要求 1.验证刚体转动定律,测定刚体绕固定轴的转动惯量 2.验证刚体转动惯量的平行轴定理: 3.验证角动量守恒定律: 4.用对称测量法消除零转引起的系统误差。 实验仪器 气垫转动惯量测定仪,专用CH山型数 字毫秒计,DC型微音气泵,砝码组(2× 1g,4×2g,及2×5g),镊子及细线等。 实验原理 1.验证刚体转动定律 转动定律指出:绕固定轴转动的刚体 其所受外力矩N与该力矩作用下产生的角 加速度成正比,即: N=la (5-1) 10 比例系数为刚体绕定轴转动的转动惯 e 量,单位:kgm。当刚体的转轴被确定 1一气室:2-定盘:3-动盘: 4一细线:5一气垫滑轮: 后,其转动惯量为一常数。如图(5-1)所 6一砝码桶:7一遮光板: 示(参见附录),由于砝码m的重力作用, 8一光电门:9-定点发放开关: 使绕在动盘圆柱上的软细线产生张力T, 10一进气口:11一地脚螺丝 在张力作用下,动盘将产生一转动力矩N。 假定动盘圆柱直径为D,则当气动阻力可忽 略时,外 图51气垫转动惯量测定仪
实验 5 气垫法测定物体的转动惯量 在很多情况下,物体的形状和大小对物体的运动规律起着重要作用,例如宏观物体的 转动,以及微观粒子如分子、原子的转动甚至电子的自转等等。在这种情况下,物体就不 能再被当作质点看待,而必须考虑物体的大小和形状,即把物体视为刚体。 在研究刚体的转动问题时,首先遇到的困难就是磨擦力矩的存在;本仪器由于采用了 气垫悬浮与气垫滑轮相结合以及气流定轴等独特设计,故该装置所有转动件间的磨擦均达 到可以忽略的程度。用它可以测量多种物体的转动惯量,能够完成转动定律、角动量守恒 定律及平行轴定理等许多实验。本实验利用气垫转动惯量测定仪测定刚体在力矩作用下转 动的角加速度,来验证刚体转动定律。 实验目的和学习要求 1.验证刚体转动定律,测定刚体绕固定轴的转动惯量; 2.验证刚体转动惯量的平行轴定理; 3.验证角动量守恒定律; 4.用对称测量法消除零转引起的系统误差。 实验仪器 气垫转动惯量测定仪,专用 CHJ 型数 字毫秒计,DC 型微音气泵,砝码组(2× 1g,4×2g,及 2×5g),镊子及细线等。 实验原理 1.验证刚体转动定律 转动定律指出:绕固定轴转动的刚体, 其所受外力矩N与该力矩作用下产生的角 加速度 成正比,即: N = I (5-1) 比例系数 I 为刚体绕定轴转动的转动惯 量,单位: 2 kg m 。当刚体的转轴被确定 后,其转动惯量为一常数。如图(5-1)所 示(参见附录),由于砝码 m 的重力作用, 使绕在动盘圆柱上的软细线产生张力 T, 在张力作用下,动盘将产生一转动力矩 N。 假定动盘圆柱直径为 D1 ,则当气动阻力可忽 略时,外 图 5-1 气垫转动惯量测定仪

力矩:N=TD (5-2) 在力矩N的作用下,动盘将作匀角加速运动,砝码m随之下落,由牛顿第二定律可 知,张力T与砝码下落的角加速度a=aD/2之间满足如下关系: T=g-a)=g-2) (5-3) 将式(5-2)及(5-3)代入式(5-1),有: N=m(g-=a (5-4) 若式(5-4)得证,则刚体转动定律得以验证。当m及D与动盘质量及半径相比均很小 时,有a<<g,于是式(5-4)变为: N=Ia≈ngD (5-5) 设动盘转动的初角速度为0,其继续转过日=2π及日,=4红角度所用的时间分别 为及2,则由刚体运动学公式可得 01=2π=0l1+am7/2 (5-6) 02=4π=042+am/2 (5-7) 由式(5-6)和(5-7)中消去0,即可求出动盘在力矩N的作用下,绕固定轴转动的角 a=4r2-1/4) 加速度: 2-41 (5-8) 改变砝码质量m,测出动盘在不同外力矩N,=m,8D下绕定轴转动的角加速度4,作 N一“曲线,若该曲线为一直线,则证明刚体转动定律成立,且直线的斜率即为刚体绕固定 轴的转动惯量1。 2.验证刚体转动惯量的平行轴定理 刚体对任一转动轴的转动惯量1等于刚体对通过其质心且平行于该轴的转动惯量'。 加上刚体的质量M乘以两平行轴间距离D的平 方。即: I=1。+MD (5-9) 这就是刚体转动惯量的平行轴定理。式(5-9)表 动盘 明,刚体的转动惯量!与其质心到转轴距离的平 图5-2动盘及圆铜柱
力矩: N = TD1 (5-2) 在力矩 N 的作用下,动盘将作匀角加速运动,砝码 m 随之下落,由牛顿第二定律可 知,张力 T 与砝码下落的角加速度 a =D1 / 2 之间满足如下关系: ( ) = − = − 2 D1 T m g a m g (5-3) 将式(5-2)及(5-3)代入式(5-1),有: I D N mD g = = − 2 1 1 (5-4) 若式(5-4)得证,则刚体转动定律得以验证。当 m 及 D1 与动盘质量及半径相比均很小 时,有 a <<g,于是式(5-4)变为: mgD1 N = I (5-5) 设动盘转动的初角速度为 0 ,其继续转过 1 = 2 及 2 = 4 角度所用的时间分别 为 1 t 及 2 t ,则由刚体运动学公式可得 2 / 2 2 1 0 1 1 = = t +t (5-6) 4 / 2 2 2 0 2 2 = = t +t (5-7) 由式(5-6)和(5-7)中消去 0 ,即可求出动盘在力矩 N 的作用下,绕固定轴转动的角 加速度: ( ) 2 1 2 1 4 2/ 1/ t t t t − − = (5-8) 改变砝码质量 mi ,测出动盘在不同外力矩 Ni = mi gD1 下绕定轴转动的角加速度 i ,作 N- 曲线,若该曲线为一直线,则证明刚体转动定律成立,且直线的斜率即为刚体绕固定 轴的转动惯量 I 。 2.验证刚体转动惯量的平行轴定理 刚体对任一转动轴的转动惯量 I 等于刚体对通过其质心且平行于该轴的转动惯量 0 I 加上刚体的质量 M 乘以两平行轴间距离 D 的平 方。即: 2 I = I 0 + MD (5-9) 这就是刚体转动惯量的平行轴定理。式(5-9)表 明, 刚体的转动惯量 I 与其质心到转轴距离的平 图 5-2 动盘及圆铜柱

方D成线性关系。当D不变时I亦不变。 (1)改变D,考察1与D的关系将质量均为M的两个铜圆柱对称地置于动盘圆柱 两侧的插孔上,如图5-2所示。设圆柱绕自身对称轴的转动惯量为'。,动盘绕自身对称 轴的转动惯量为'。,两轴间距离为D,整体系统的转动惯量为1,则据平行轴定理有: I-1。+2L.+MD') (5-10) 1=mgD mD 又由式(5-4)可知,整体系统的转动惯量为: 2 (5-11) 式(5-11)中,D1表示动盘圆柱直径:(表示砝码桶及砝码质量为m时系统转动的角加 速度,且由式(5-7)可知: 12-41 4-4) a4x2/2-1/44z24,-) (5-12) 式(5-12)中,4及'2分别表示系统旋转一周及两周所用的时间。将式(5-11)代入式(5-10), 1=4+BD 整理后得: (5-13) 若在直角坐标系内1/a~D'关系为一条直线,则式(5-13)亦即式(5-10)成立,刚体 转动惯量的平行轴定理得以验证。且直线的截距A和斜率B分别为: A=6+2+ D mgD 2g (5-14) 2M 及 B-mgD (5-15) (2)D不变,只改变刚体的方位 将质量均为M'的两个长方体铝块对 (1) (2) (3) 称地置于动盘圆柱两侧的插孔上,在 保持铝块质心与动盘中心轴的距离D'恒定的情 图53动盘及铝块 况下,改变铝块方位,如图5-3所示
方 2 D 成线性关系。当 D 不变时 I 亦不变。 (1)改变 D,考察 I 与 D 2 的关系将质量均为 M 的两个铜圆柱对称地置于动盘圆柱 两侧的插孔上,如图 5-2 所示。设圆柱绕自身对称轴的转动惯量为 c I ,动盘绕自身对称 轴的转动惯量为 0 I ,两轴间距离为 D,整体系统的转动惯量为 I ,则据平行轴定理有: 2( ) 2 I = I 0 + I c + MD (5-10) 又由式(5-4)可知,整体系统的转动惯量为: 2 2 mgD1 mD1 I = − (5-11) 式(5-11)中,D 1 表示动盘圆柱直径; 表示砝码桶及砝码质量为 m 时系统转动的角加 速度,且由式(5-7)可知: ( ) ( ) ( ) 1 2 1 2 2 1 2 1 2 1 4 2/ 1/ 4 2 1 t t t t t t t t t t − − = − − = (5-12) 式(5-12)中, 1 t 及 2 t 分别表示系统旋转一周及两周所用的时间。将式(5-11)代入式(5-10), 整理后得: 1 2 = A + BD (5-13) 若在直角坐标系内 2 1/ ~ D 关系为一条直线,则式(5-13)亦即式(5-10)成立,刚体 转动惯量的平行轴定理得以验证。且直线的截距 A 和斜率 B 分别为: g D mgD I I A c 2 2 1 1 0 + + = (5-14) 及 B= 1 2 mgD M (5-15) (2)D 不变,只改变刚体的方位 将质量均为 M 的两个长方体铝块对 称地置于动盘圆柱两侧的插孔上,在 保持铝块质心与动盘中心轴的距离 D 恒定的情 况下,改变铝块方位,如图 5-3 所示, 图 5-3 动盘及铝块

分别使两铝块长轴(1)平行、(2)垂直及(3)重合等。若在上述情况下,测得系统转动 一周及两周所需要的时间对应相等,亦即角加速度相等,则说明:当转轴确定后,刚体的 转动惯量 =h=+MD 2 (5-16) 只与其通过质心且平行于固定轴的转动惯量:及平行轴间距D'有关,而与刚体相对于自 身转轴转过的角度无关。它又从另一个侧面证实了平行轴定理。式(5-16)中,若测定了 动盘及整体系统的转动惯量'0及,则可求出铝块的转动惯量'。 3.验证角动量守恒定律 质点绕定轴转动的角动量L定义为其矢径r与其动量P的矢乘积,即:L=Xp。由 此可以证明,刚体绕固定轴转动的角动量,等于刚体相对于该轴的转动惯量Ⅰ乘以刚体转 动的角速度0,且其方向与角速度的方向相同,以数值表示时,为: L-@ (5-17) 当刚体在外力矩N的作用下,以角加速度a=dO/h转动时,即服从转动定律。显然, 描述刚体转动定律的式(5-1)即为式(5-17)对时间t的微商: N=dL/dh=I.(doldt) (5-18) 而当合外力矩为零时,角动量不随时间变化,即: L=I0=恒量 (5-19) 式(5-19)即角动量守恒定律。 角动量的概念及角动量守恒定律在原子物理、量 子物理及基本粒子的研究中都有很重要的作用。本实 验就是在气垫转动惯量测定仪上验证角动量守恒定 1一压缩空气:2-光电门: 律。将气垫转动惯量测定仪主体(图5-1)去掉动盘、 2一挡光板: 4定位板 细线及砝码桶,并与其附件(4)一起装配如图5-4所 5一固定板:6一圆柱式定位器 示。提起细尼龙绳,使金属球与凹盘脱离并被圆柱式 1一尼龙线: 8一金属球: 定位器嵌住,保持角速度为零。若某时刻使金属球轻 9一凹盘: 10一定位开关 缓地对心落于正以 图5-4气垫转盘与附件(4)装配 角速度)旋转的凹 盘上,二者合为一体,并以另一角速度2旋转,设凹盘与金属球绕其自身对称轴的转动 惯量分别为及2,则因合外力矩为零而满足角动量守恒定律,即:
分别使两铝块长轴(1)平行、(2)垂直及(3)重合等。若在上述情况下,测得系统转动 一周及两周所需要的时间对应相等,亦即角加速度相等,则说明:当转轴确定后,刚体的 转动惯量 1 0 2 2 I M D I I I c = + − = (5-16) 只与其通过质心且平行于固定轴的转动惯量 c I 及平行轴间距 D 有关,而与刚体相对于自 身转轴转过的角度无关。它又从另一个侧面证实了平行轴定理。式(5-16)中,若测定了 动盘及整体系统的转动惯量 0 I 及 1 I ,则可求出铝块的转动惯量 I。 3.验证角动量守恒定律 质点绕定轴转动的角动量 L 定义为其矢径 r 与其动量 P 的矢乘积,即:L=r×p。由 此可以证明,刚体绕固定轴转动的角动量,等于刚体相对于该轴的转动惯量 I 乘以刚体转 动的角速度 ,且其方向与角速度的方向相同,以数值表示时,为: L=I (5-17) 当刚体在外力矩 N 的作用下,以角加速度 = d/ dt 转动时,即服从转动定律。显然, 描述刚体转动定律的式(5-1)即为式(5-17)对时间 t 的微商: N = dL/ dt = I ( d / dt ) (5-18) 而当合外力矩为零时,角动量不随时间变化,即; L = I = 恒量 (5-19) 式(5-19)即角动量守恒定律。 角动量的概念及角动量守恒定律在原子物理、量 子物理及基本粒子的研究中都有很重要的作用。本实 验就是在气垫转动惯量测定仪上验证角动量守恒定 律。将气垫转动惯量测定仪主体(图 5-1)去掉动盘、 细线及砝码桶,并与其附件(4)一起装配如图 5-4 所 示。提起细尼龙绳,使金属球与凹盘脱离并被圆柱式 定位器嵌住,保持角速度为零。若某时刻使金属球轻 缓地对心落于正以 角速度 1 旋转的凹 盘上,二者合为一体,并以另一角速度 2 旋转,设凹盘与金属球绕其 自身对称轴的转动 惯量分别为 1 I 及 2 I ,则因合外力矩为零而满足角动量守恒定律,即: 图 5-4 气垫转盘与附件(4)装配

I0,=(41+12)0 (5-20) 若以4、52分别表示金属球与凹盘合成一体前、后转过2π所用的时间,则式(5-20) 1+12-01-2π/h-2 变为: 1022π/1341 (5-21) 式(5-21),4、12即凹盘上的平板挡光片在两种情况下转过2π弧度的时间。而I1及'2 则可由下述方法测得:将气垫转动惯量测定仪恢复成图5-1主体结构所示的状态。然后将 转动惯量接插座扣在动盘圆柱上(插脚向上),参照实验2的方法,测出动盘与接插座系 统的转动惯量6。之后,将凹盘插在转动惯量接插座的插脚上(图5-5),以同样方法测 出动盘、接插座和凹盘系统的转动惯量【。由此求得凹盘的转动惯量: 1=1-16 (5-22) 最后,将凹盘取下,翻转转动惯量接插座(将其 插脚插入动盘圆柱的中心孔内),再把金属球置 于转动惯量接插座的凹面上,即可以相同方法测 出动盘、接插座和金属球整个系统的转动惯'。 于是,金属球的转动惯量: L,='-I6 (5-23) 将式(5-23)代入(5-23)代入式(5-22),得 1一压缩空气:2-光电门: 1+1r-2- 3一挡光板:4一转动惯量插接座 1-6 5一气垫滑轮:6一定位开关 7-动盘:8一凹盘:9细线 (5-24) 若式(5-24)成立,则式(5-19)成立,即角动 量守恒定律得证。 仪器的使用及调节方法 1.气垫转盘承重21×10kg/P口、故当负载2kg待测样品(包括动盘)时,所提 供的气压应不小于2kPa。气源压力应视负载大小而定,一般可选2~3kPa。 2.气垫转动惯量测定仪使用前应调节水平。方法是:取下动盘,接通气源,将水平 校准盘置于气室上表面中央,调节地脚螺丝(11),使校准盘稳定地飘浮于气室中央,或 其各质点绕定盘内侧空腔四壁均匀而缓慢地作滚轮线运动,且改变旋轮方向时其运动方式 不变
1 1 1 2 2 I = (I + I ) (5-20) 若以 1 t 、 2 t 分别表示金属球与凹盘合成一体前、后转过 2 所用的时间,则式(5-20) 变为: 1 2 2 1 2 1 1 1 2 2 / 2 / t t t t I I I = = = + (5-21) 式(5-21), 1 t 、 2 t 即凹盘上的平板挡光片在两种情况下转过 2 弧度的时间。而 1 I 及 2 I 则可由下述方法测得:将气垫转动惯量测定仪恢复成图 5-1 主体结构所示的状态。然后将 转动惯量接插座扣在动盘圆柱上(插脚向上),参照实验 2 的方法,测出动盘与接插座系 统的转动惯量 0 I 。之后,将凹盘插在转动惯量接插座的插脚上(图 5-5),以同样方法测 出动盘、接插座和凹盘系统的转动惯量 I 。由此求得凹盘的转动惯量: 1 0 I = I − I (5-22) 最后,将凹盘取下,翻转转动惯量接插座(将其 插脚插入动盘圆柱的中心孔内),再把金属球置 于转动惯量接插座的凹面上,即可以相同方法测 出动盘、接插座和金属球整个系统的转动惯 I 。 于是,金属球的转动惯量: 2 0 I = I − I (5-23) 将式(5-23)代入(5-23)代入式(5-22),得 1 2 0 2 0 t t I I I I I = − + − (5-24) 若式(5-24)成立,则式(5-19)成立,即角动 量守恒定律得证。 仪器的使用及调节方法 1.气垫转盘承重 1 10 kg / Pa −3 、故当负载 2kg 待测样品(包括动盘)时,所提 供的气压应不小于 2kPa。气源压力应视负载大小而定,一般可选 2~3kPa。 2.气垫转动惯量测定仪使用前应调节水平。方法是: 取下动盘,接通气源,将水平 校准盘置于气室上表面中央,调节地脚螺丝(11),使校准盘稳定地飘浮于气室中央,或 其各质点绕定盘内侧空腔四壁均匀而缓慢地作滚轮线运动,且改变旋轮方向时其运动方式 不变

3.气垫滑轮的调节。气垫滑轮的调节包括两项内容:其一,使气垫滑轮在空载情况 下运动自如,且无附加力矩。方法是:先调节滑轮两端定位圈,使与滑轮间隙约为0.5mm: 再调节滑轮高度及轴向水平,使细线与动盘平面水平:取下细线,在高度及水平程度不变 的前提下,旋转滑轮的方向,使其气孔密集处位于外侧上方45℃左右,直至滑轮在负 载情况下能正、反两个方向保持惯性运动状态或相对静止。其二,动盘顺时针或逆时针运 动时,都应首先旋动滑轮支架,使细线与滑轮轴向垂直。 仪器的使用规则 1.特别注意:未开气源时,动盘不得人为地在气室表面磨擦转动,气室、气垫滑轮 及诸连接管道均不得漏气。 2.每次使用前,应在接通气源的情况下,以蘸有酒精的软细布轻拭气室及动盘的上、 下表面,以防气孔堵塞或被尘粒划伤表面。 3.实验前,应调节气室上表面水平,使处于正常状态,且调好后不得随意哪动。 4.整个实验过程中要求气压稳定不变。 5.安装、调节及使用该装置时,操作应细心谨慎,严禁磕碰动盘、定盘、气垫滑轮、 水平校准盘、金属球、圆柱式定位器、转动惯量接插座、铜圆柱、铝块及凹盘等,更不得 使其坠落地 实验内容 1.验证刚体转动定律 (1)接通气源、取下动盘、放上水平校准盘再调节地脚螺丝使定盘及气室上表面处 于水平状态。 (2)将仪器各部分均调到正常状态。主要包括:气垫滑轮运转自如且无附加力矩, 细线自然缠绕于动盘圆柱时,应与动盘平面平行,且细线应分别与气垫滑轮轴向垂直:两 端砝码桶基本等高:聚光灯泡对准光敏二极管,且光控计时正常等。 (3)依次向两个砝码桶(其质量相等5g)内放入等量砝码,分别在不同力矩作用下 以数字毫秒计测定动盘旋转一周(即8=2π)及两周(82=4r)所需的时间1及2各 3次:给动盘施加转动力矩的方向是逆时针在动盘圆柱上绕线3周以上。采用数字毫秒计 测动盘旋转一周及两周的时间。 (4)为采用对立影响法消除动盘可能产生的零转引起的系统误差,使动盘按相反方 向旋转,并重复3中所述的测量:但测量前,应重新调整气垫滑轮轴线与细线垂直。 1.1.在不同力矩作用下,侧定动盈转动的角加速度(见下表)。 1.2.据下表中的数据,在直角坐标纸上,以N为横坐标,为纵坐标,作水曲线 验证刚体转动定律,并由直线斜率求动盘的转动惯量!。 动盘顺时针旋转时单位制(S1):g=9.8m/s2:D,=2×10-2m 则量 i 次数 123 123123 123 123 m
3.气垫滑轮的调节。气垫滑轮的调节包括两项内容:其一,使气垫滑轮在空载情况 下运动自如,且无附加力矩。方法是:先调节滑轮两端定位圈,使与滑轮间隙约为 0.5mm; 再调节滑轮高度及轴向水平,使细线与动盘平面水平;取下细线,在高度及水平程度不变 的前提 下,旋转滑轮的方向,使其气孔密集处位于外侧上方 45℃左右,直至滑轮在负 载情况下能正、反两个方向保持惯性运动状态或相对静止。其二,动盘顺时针或逆时针运 动时,都应首先旋动滑轮支架,使细线与滑轮轴向垂直。 仪器的使用规则 1.特别注意:未开气源时,动盘不得人为地在气室表面磨擦转动,气室、气垫滑轮 及诸连接管道均不得漏气。 2.每次使用前,应在接通气源的情况下,以蘸有酒精的软细布轻拭气室及动盘的上、 下表面,以防气孔堵塞或被尘粒划伤表面。 3.实验前,应调节气室上表面水平,使处于正常状态,且调好后不得随意挪动。 4.整个实验过程中要求气压稳定不变。 5.安装、调节及使用该装置时,操作应细心谨慎,严禁磕碰动盘、定盘、气垫滑轮、 水平校准盘、金属球、圆柱式定位器、转动惯量接插座、铜圆柱、铝块及凹盘等,更不得 使其坠落地 实验内容 1.验证刚体转动定律 (1)接通气源、取下动盘、放上水平校准盘再调节地脚螺丝使定盘及气室上表面处 于水平状态。 (2)将仪器各部分均调到正常状态。主要包括:气垫滑轮运转自如且无附加力矩, 细线自然缠绕于动盘圆柱时,应与动盘平面平行,且细线应分别与气垫滑轮轴向垂直;两 端砝码桶基本等高;聚光灯泡对准光敏二极管,且光控计时正常等。 (3)依次向两个砝码桶(其质量相等 5g)内放入等量砝码,分别在不同力矩作用下 以数字毫秒计测定动盘旋转一周(即 1 = 2 )及两周( 2 = 4 )所需的时间 t1 及 t2 各 3 次;给动盘施加转动力矩的方向是逆时针在动盘圆柱上绕线 3 周以上。采用数字毫秒计 测动盘旋转一周及两周的时间。 (4)为采用对立影响法消除动盘可能产生的零转引起的系统误差,使动盘按相反方 向旋转,并重复 3 中所述的测量;但测量前,应重新调整气垫滑轮轴线与细线垂直。 1.1.在不同力矩作用下,测定动盘转动的角加速度(见下表)。 1.2.据下表中的数据,在直角坐标纸上,以 N 为横坐标, 为纵坐标,作 N- 曲线, 验证刚体转动定律,并由直线斜率求动盘的转动惯量 I 。 动盘顺时针旋转时单位制(SI): g m s D m 2 1 2 9.8 / ; 2 10− = = 测量 次数 i 1 2 3 4 5 j 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 物 m i
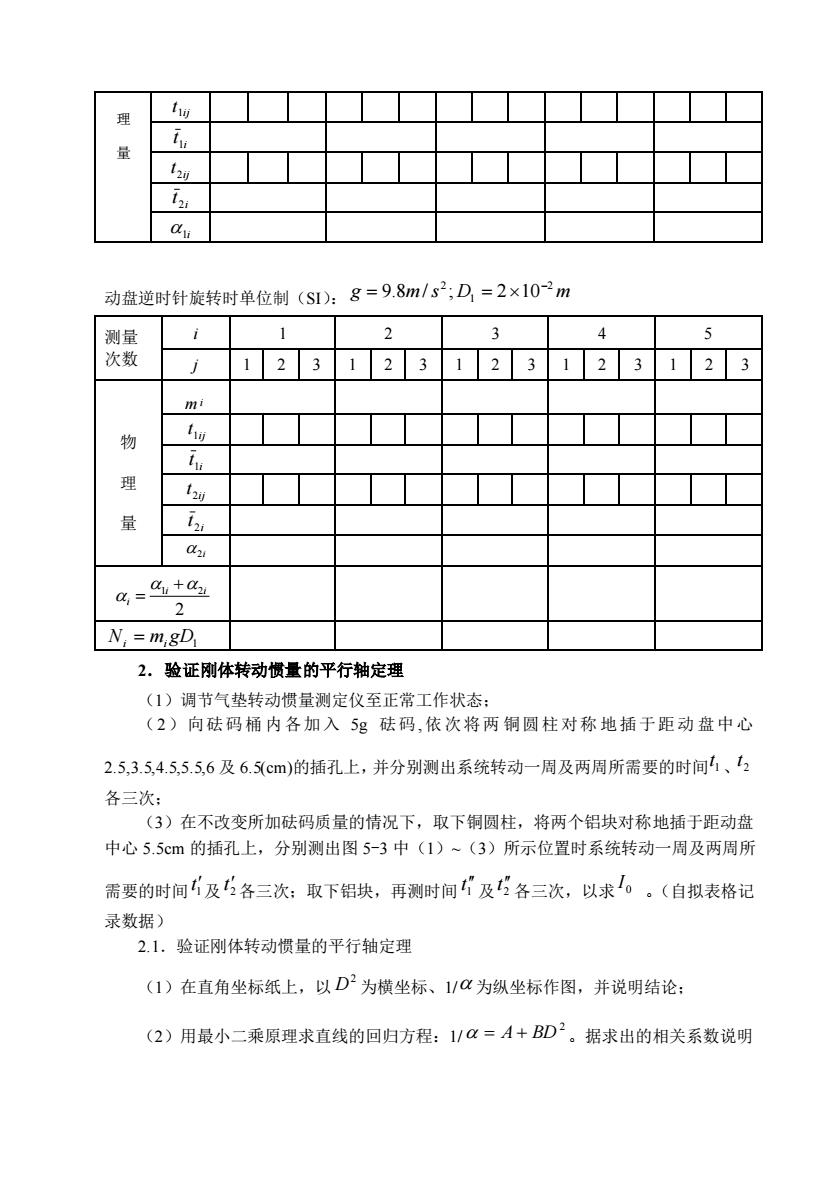
动盘逆时针旋转时单位制(SD:8=9.8m/s;D=2×102m 测量 2 3 5 次数 123123123123123 mi 物 C N =mgD 2.验证刚体转动惯量的平行轴定理 (1)调节气垫转动惯量测定仪至正常工作状态: (2)向砝码桶内各加入5g砝码,依次将两铜圆柱对称地插于距动盘中心 2.5,3.5,4.5,5.5,6及6.5(cm)的插孔上,并分别测出系统转动一周及两周所需要的时间、2 各三次: (3)在不改变所加砝码质量的情况下,取下相圆柱,将两个铝块对称地插于距动盘 中心5.5cm的插孔上,分别测出图5-3中(1)~(3)所示位置时系统转动一周及两周所 需要的时间及5各三次:取下铝块,再测时间及5各三次,以求'。。(自拟表格记 录数据) 2.1.验证刚体转动惯量的平行轴定理 (1)在直角坐标纸上,以D2为横坐标、1/C为纵坐标作图,并说明结论: (2)用最小二乘原理求直线的回归方程:1/=A+BD2。据求出的相关系数说明
理 量 ij t 1 i t 1 ij t 2 i t 2 1i 动盘逆时针旋转时单位制(SI): g m s D m 2 1 2 9.8 / ; 2 10− = = 测量 次数 i 1 2 3 4 5 j 1 2 3 1 2 3 1 2 3 1 2 3 1 2 3 物 理 量 m i ij t 1 i t 1 ij t 2 i t 2 2i 1 2 2 i i i + = Ni = mi gD1 2.验证刚体转动惯量的平行轴定理 (1)调节气垫转动惯量测定仪至正常工作状态; (2)向砝码桶 内各加入 5g 砝码, 依次将两 铜圆柱对称 地插于距动 盘中心 2.5,3.5,4.5,5.5,6 及 6.5(cm)的插孔上,并分别测出系统转动一周及两周所需要的时间 1 t 、 2 t 各三次; (3)在不改变所加砝码质量的情况下,取下铜圆柱,将两个铝块对称地插于距动盘 中心 5.5cm 的插孔上,分别测出图 5-3 中(1)~(3)所示位置时系统转动一周及两周所 需要的时间 1 t 及 2 t 各三次;取下铝块,再测时间 1 t 及 2 t 各三次,以求 0 I 。(自拟表格记 录数据) 2.1.验证刚体转动惯量的平行轴定理 (1)在直角坐标纸上,以 2 D 为横坐标、1/ 为纵坐标作图,并说明结论; (2)用最小二乘原理求直线的回归方程:1/ 2 = A + BD 。据求出的相关系数说明

结论。并由A、B之值求'及M。 单位制:S1:D,=2×102;8=2x,8,=4r,m=0.01kg 2.2.D不变,测定铝块与动盘系统转动的角加速度 (1)由心的计算结果说明结论: (2)由a'及式(5-11)求系统的转动惯量I1: a'=∑a,13= 1=mgD_mD am'2= 单位制:S1:D=2×1028=9.8m=0.01kgD=5.5x10 23.测定动盘的转动惯量。 单位制:S1:D,=2×102:g=9.8m=0.01kg 1,-mg2_m0- r=4-= 2 3.验证角动量守恒定律(选作) (1)调节气垫转动惯量测定仪使其达到正常工作状态: (2)参照图55(不包括凹盘),向砝码桶内各加入5g砝码,分别在顺时针和逆时 针两个方向测出其旋转一周及两周所用的时间、如及6:、各三次,求转动惯量6: (3)放上凹盘,以同样方法测出、公及、各三次,以求转动惯量1: (4)取下凹盘,将转动惯量接插座翻转,置上金属球。以同样的方法测出1、如及 、各三次,以求转动惯量': (5)取下动盘及砝码桶,换上凹盘。参照图5-4安装圆柱式定位器,调整其位置 使金属球能相对凹盘对心下落。安装与调整方法如下:将悬挂金属球的细尼龙线自下而 上穿过已旋去上部螺母的圆柱式定位器通孔,手持金属球与定位器,将定位螺杆穿入矩 形框架横梁的中心通孔,手提金属球并将其平稳地放在凹盘凹面内,圆柱式定位器倒扣 在金属球正上方,套上定位板,旋入上部螺母,至金属球与定位器凹面间距1~2mm。此 时,按住定位板,当提、落金属球时,球不应在凹盘凹面内摆动。检验方法是:在通有 气源的情况下,旋转凹盘,待转稳后,反复提、落金属球,凹盘及球均不应有明显摆动
结论。并由 A、B 之值求 c I 及 M。 单位制:SI: = = = = − D 2 10 ; 2 ; 2 4 ;m 2 1 0.01kg 2.2. D 不变,测定铝块与动盘系统转动的角加速度 (1)由 J 的计算结果说明结论; (2)由 及式(5-11)求系统的转动惯量 1 I : = = = 3 1 / 3 J J 2 2 1 1 1 mgD mD I − = = 单位制:SI; 2 2 1 2 10 ; 9.8; 0.01 ; 5.5 10 − − D = g = m = kg D = 2.3.测定动盘的转动惯量 0 I 单位制:SI; 2 10 ; 9.8; 0.01 2 1 = = = − D g m kg − = = 2 2 1 1 0 mgD mD I = − = 2 1 0 I I I 3.验证角动量守恒定律(选作) (1)调节气垫转动惯量测定仪使其达到正常工作状态; (2)参照图 5-5(不包括凹盘),向砝码桶内各 加入 5g 砝码,分别在顺时针和逆时 针两个方向测出其旋转一周及两周所用的时间 01 t 、 02 t 及 01 t 、 02 t 各三次,求转动惯量 0 I ; (3)放上凹盘,以同样方法测出 11 t 、 12 t 及 11 t 、 12 t 各三次, 以求转动惯量 I ; (4)取下凹盘,将转动惯量接插座翻转,置上金属球。以同样的方法测出 21 t 、 22 t 及 21 t 、 22 t 各三次,以求转动惯量 I ; (5)取下动盘及砝码桶,换上凹盘。参照图 5-4 安装圆柱式定位器,调整其位置, 使金属球能相对凹盘对心下落。安装与调整方法如下:将悬挂金属球的细尼龙线自下而 上穿过已旋去上部螺母的圆柱式定位器通孔,手持金属球与定位器,将定位螺杆穿入矩 形框架横梁的中心通孔,手提金属球并将其平稳地放在凹盘凹面内,圆柱式定位器倒扣 在金属球正上方,套上定位板,旋入上部螺母,至金属球与定位器凹面间距 1~2mm。此 时,按住定位板,当提、落金属球时,球不应在凹盘凹面内摆动。检验方法是:在通有 气源的情况下,旋转凹盘,待转稳后,反复提、落金属球,凹盘及球均不应有明显摆动

最后旋紧固定螺丝,圆柱式定位器即安装完毕。 (6)人为给定一平稳的角速度,连续测出金属球未落下(凹盘)与已落下(凹盘与 金属球合系统)时平板挡光片遮光时间1及2各四次,以分别求出角速度o1及ω2。由 计算结果说明验证结论。 思考题 1.能否用本仪器验证刚体运动学公式:日=0o1+12?若能,应怎样进行实验? 2.本实验操作中,如果不要求采取正、反两个方向旋转,即不要求采用对立影响法 进行实验。如此操作,对实验有无影响?请具体说明之。 3.本实验若采用对称测量方法,能消除或减弱哪种系统误差?相应的数据处理应如 何进行?此外还存在系统误差吗?对实验有何影响? 4.试由计算公式,求出一个铝块绕动盘中心轴旋转时的转动惯量),与实验结果' 进行比较,并分析原因。己知转轴与铝块的高“c”平行,铝的密度P=2700kg/m, 平行轴间距D'=5.5cm,且铝块的长、宽、高分别为:a=6.0cm,b=4.0cm,c=3.0cm
最后旋紧固定螺丝,圆柱式定位器即安装完毕。 (6)人为给定一平稳的角速度,连续测出金属球未落下(凹盘)与已落下(凹盘与 金属球合系统)时平板挡光片遮光时间 t1 及 t2 各四次,以分别求出角速度 ω1及 ω2。由 计算结果说明验证结论。 思考题 1.能否用本仪器验证刚体运动学公式: / 2? 2 0 = t +t 若能,应怎样进行实验? 2.本实验操作中,如果不要求采取正、反两个方向旋转,即不要求采用对立影响法 进行实验。如此操作,对实验有无影响?请具体说明之。 3.本实验若采用对称测量方法,能消除或减弱哪种系统误差?相应的数据处理应如 何进行?此外还存在系统误差吗?对实验有何影响? 4.试由计算公式,求出一个铝块绕动盘中心轴旋转时的转动惯量 0 I ,与实验结果 I 进行比较,并分析原因。已知转轴与铝块的高“c”平行,铝的密度 3 = 2700kg / m , 平行轴 间距 D = 5.5cm ,且铝块的长、宽、高分别为: a = 6.0cm,b = 4.0cm,c = 3.0cm.