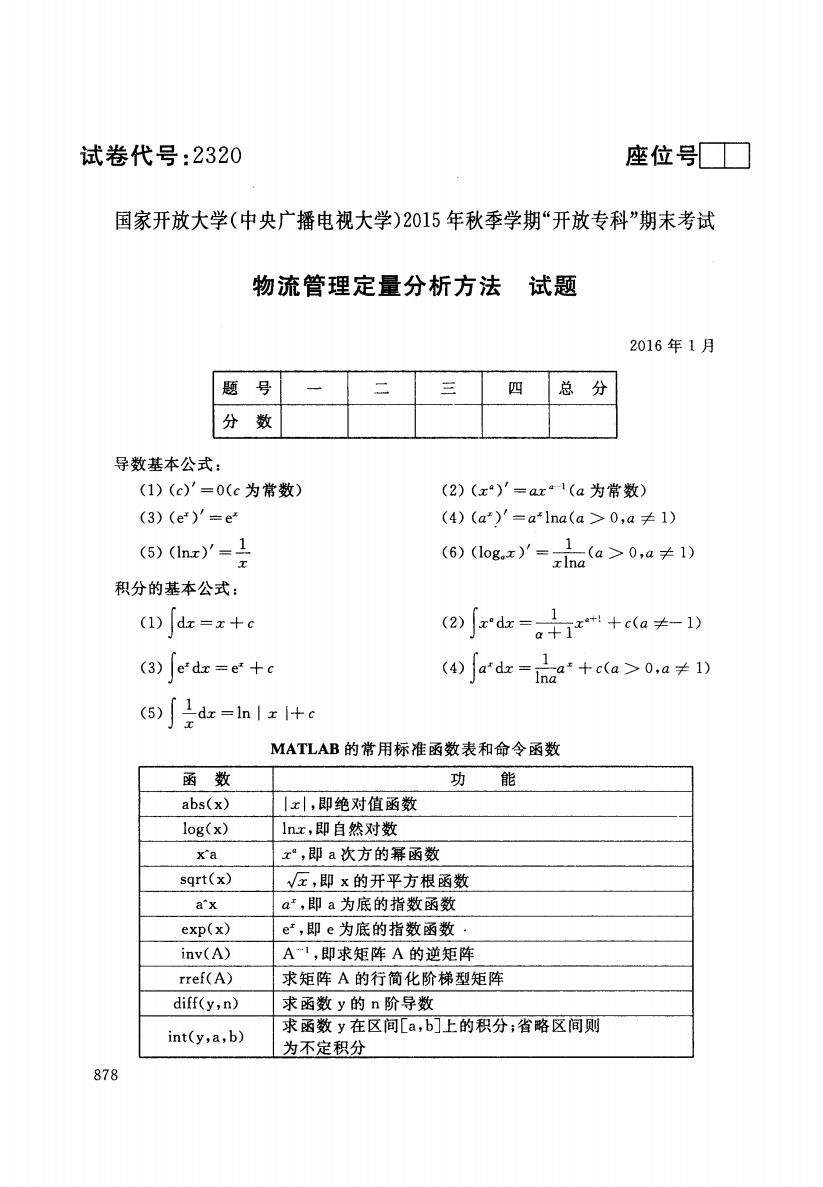
试卷代号:2320 座位口 国家开放大学(中央广播电视大学)2015年秋季学期“开放专科”期末考试 物流管理定量分析方法试题 2016年1月 题号 三 四 总分 分数 导数基本公式: (1)(c)'=0(c为常数) (2)(x)'=ax1(a为常数) (3)(e)'=e (4)(a)'=alna(a>0,a≠1) (6)(Ixy= (60ox)r-a>0.a≠D 积分的基本公式: (1)d=x+c 2d-x+a≠-) (3)∫crdx=e+c )fadz=a+ca>0a≠D (5)∫上dz=lnlx+c MATLAB的常用标准函数表和命令函数 函数 功能 abs(x) x|,即绝对值函数 log(x) lnx,即自然对数 xa x,即a次方的幂函数 sqrt(x) √:,即x的开平方根函数 a'x a',即a为底的指数函数 exp(x) e,即e为底的指数函数· inv(A) A1,即求矩阵A的逆矩阵 rref(A) 求矩阵A的行简化阶梯型矩阵 diff(y,n) 求函数y的n阶导数 int(y,a,b) 求函数y在区间[a,b]上的积分;省略区间则 为不定积分 878
试卷代号 :2320 座位号 国家开放大学(中央广播电视大学)2015 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题 2016 E E 导数基本公式: (1) (c)' =O(c 为常数〉 (3) (e)' =eX (5) (\nx)' = 1... z (2) (x.)' .--1 (a 为常数) (4) (αX)' =axlna( >O 手1) (6)(logaZ)'=J (α >O 手1) xlna 积分的基本公式: (1) fdx=x+c Xdx 刊:千: td缸←=ln I x MATLAB 的常用标准函数表和命令函数 (2)lx.dx= --:;-x.+ + c( 叫一1) J 寸- -L (4)iazdz=TLaz c(a > ,叫1) J ma abs(x) Ixl ,即绝对值函数 log(x) lnx ,即自然对数 x-a za ,即 次方的幕函数 sqrt(x) .[i, 的开平方根函数 a-x ,即 为底的指数函数 exp(x) 为底的指数函数, Ìnv(A) 寸,即求矩阵 的逆矩阵 rref(A) 求矩阵 的行简化阶梯型矩阵 diff(y , n) 求函数 阶导数 int(y , a , b) 求函数 在区间 [a ,盯上的积分;省略区间则 为不定积分 878

得分 评卷人 一、单项选择题(每小题4分,共20分) 1.若某物资的总供应量大于总需求量,可增设一个虚销地,其需求量取总供应量与总需 求量的差额,并取各产地到该销地的单位运价为0,则可将( )运输问题化为供求平衡运输 问题。 A.供不应求 B.供需平衡 C.供过于求 D.供求平衡 2.某物流公司有三种化学原料A1,A2,A3。每公斤原料A1含B,B2,B,三种化学成分 的含量分别为0.7公斤、0.2公斤和0.1公斤:每公斤原料A2含B1,B2,B的含量分别为0.1 公斤、0.3公斤和0.6公斤;每公斤原料A,含B,B2,B的含量分别为0.3公斤、0.4公斤和 0.3公斤。每公斤原料A1,A2,A,的成本分别为500元、300元和400元。今需要B1成份至 少100公斤,B2成份至少50公斤,B,成份至少80公斤。为列出使成本最小的线性规划模型, 设需要原料A:,A2,A,的数量分别为x1公斤、x2公斤和x3公斤,则化学成分B2应满足的约 束条件为()。 A.0.2x1十0.3x2+0.4x3<100 B.0.2.x1+0.3x2+0.4x3≥100 C.0.2x1+0.3x2+0.4x3=100 D.0.2x1+0.3x2+0.4x3≤100 3.下列矩阵中,( )是单位矩阵。 10] 017 A. B. 1 0 0 17 1 0] C. D. 01 1 o 4.设某公司运输某物品的总收人(单位:千元)函数为R(q)=100q一0.1gq,则运输量为 100单位时的边际收入为( )千元/单位。 A.90 B.9000 C.80 D.8900 5.由曲线y=x3,直线x=1与x=2,以及x轴围成的曲边梯形的面积表示为( )。 A.dz B.'dx C.= D.z'dx 879
|得分|评卷人| l 一、单项选择题{每小题 分,共 20 分} 1.若某物资的总供应量大于总需求量,可增设一个虚销地,其需求量取总供应量与总需 求量的差额,并取各产地到该销地的单位运价为 o. 则可将( )运输问题化为供求平衡运输 问题。 A. 供不应求 c. 供过于求 B. 供需平衡 o. 供求平衡 2. 某物流公司有三种化学原料 Al .A2 .A3 每公斤原料 Al Bl , B2 .B3 三种化学成分 的含量分别为 o. 公斤、O. 公斤和 0.1 公斤;每公斤原料 Az Bl' .B 的含量分别为 O. 1 公斤、 0.3 公斤和 0.6 公斤;每公斤原料 A3 含矶,也,民的含量分别为 0.3 公斤、 0.4 公斤和 0.3 公斤。每公斤原料儿 .A2.A3 的成本分别为 500 元、 300 元和 400 元。今需要 Bl 成份至 100 公斤 .B2 成份至少 50 公斤,且成份至少 80 公斤。为列出使成本最小的线性规划模型, 设需要原料儿 .A .儿的数量分别为 Xl 公斤、X2 公斤和岛公斤,则化学成分 应满足的约 束条件为 )。 A. o. 2Xl 0. 3X 0.4均< 100 B. o. 2Xl + o. 3X2 + o. 4X3 100 c. o. 2Xl + o. 3X2 O. 4X3 = 100 0.0. 2X 0. 3X O. 4X3 ~ 100 3. 下列矩阵中. ( )是单位矩阵。 A. [~ ~] c. [: ~] B. [~ ~] O. [~ :] 4. 设某公司运输某物品的总收入(单位:千元〉函数为 R(q) = 100q o. 1q2. 则运输量为 100 单位时的边际收入为)千元/单位。 A.90 C. 80 B. 9000 0.8900 5. 由曲线 Y=X 直线工 =1 x=2 以及工轴围成的曲边梯形的面积表示为( )。 Z JU Z FEElztd A Z ' B Z c. = J: x 3 dx z d z P--t1d ZI D 879

得分 评卷人 二、计算题(每小题9分,共27分) 3 -21r 10 2 6.已知矩阵A= ,B= 2 1 ,求:A+BT 01-1 3 7.设y=(x3+2)e,求:y 8.计算定积分: f(1+32+e)dr 得 分 评卷人 三、编程题(每小题9分,共27分) 已知矩阵A= 9. 。 试写出用MATLAB软件计算 矩阵表达式A1+BCT的命令。 10.试写出用MATLAB软件计算函数y=a.n(9十√/x+4)的二阶导数的命令语句. 11.试写出用MATLAB软件计算不定积分的,3(x2+e)dx命令语句. 得 分 评卷人 四、应用题(第12题18分,第13题8分,共26分) 12.某公司从A,B,C三个产地运输某物资到I,Ⅱ,Ⅲ三个销地,各产地的供应量(单位: 吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示: 运输平衡表与运价表 销地 产地 供应量 Ⅲ A 50 9 12 20 B 40 8 16 11 C 30 14 15 10 销量 40 20 60 120 (1)在上表中写出用最小元素法编制的初始调运方案(用其它方法不计成绩); (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 880
二、计算题(每小题 分,共 27 分} A + B T T B nihv ol , hu 7. = (X3 + 2) 矿,求 :YF 计算定积分: f: (1 + 白白 三、编程题(每小题 分,共 27 分) 11 r 1 0 I r 2 - 11 已知矩阵 A=L 1l ,B=L A,c=Ll A 。试写出用 MATLAB 软件计算 矩阵表达式 A-1+BC 的命令。 10. 试写出用 MATLAB 软件计算函数 y= .ln(9+ v' +4) 的二阶导数的命令语句。 11 试写出用 MA1 川软件讨算不定积分的 f: 叫十的叫令语句。 四、应用题{第 12 18 分,第 13 分,共 26 分) 12. 某公司从 三个产地运输某物资到 , n ,田三个销地,各产地的供应量(单位: 吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表所示: 运输平衡表与运价表 主汪\\芝? I E 供应量 I E A 50 9 12 20 B 40 8 16 11 C 30 14 15 10 销量 40 20 60 120 一一一一一一一一 (1)在上表中写出用最小元素法编制的初始调运方案(用其它方法不计成绩) ; (2) 检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运‘输总 费用。 880

13.某物流公司下属企业经过对近期销售资料分析及市场预测得知,该企业生产的甲、 乙、丙三种产品,均为市场紧俏产品。今已知上述每件产品的原材料消耗定额分别为4公斤、5 公斤和6公斤;上述每件产品所需工时分别为2台时、3台时和5台时。另外,上述每件产品 的利润分别为3百元、5百元和4百元。因每天生产所需原材料和工时限额分别为180公斤、 200台时。试建立在上述条件下,使企业获得利润最大的线性规划模型,并写出用MATLAB 软件计算该线性规划问题的命令语句。 881
13. 某物流公司下属企业经过对近期销售资料分析及市场预测得知,该企业生产的甲、 乙、丙三种产品,均为市场紧俏产品。今已知上述每件产品的原材料消耗定额分别为 公斤、 公斤和 公斤;上述每件产品所需工时分别为 台时、 台时和 台时。另外,上述每件产品 的利润分别为 百元、 百元和 百元。因每天生产所需原材料和工时限额分别为 180 公斤、 200 台时。试建立在上述条件下,使企业获得利润最大的线性规划模型,并写出用 MATLAB 软件计算该线性规划问题的命令语句。 881

试卷代号:2320 国家开放大学(中央广播电视大学)2015年秋季学期“开放专科”期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考) 2016年1月 一、单项选择题(每小题4分,共20分)】 1.C 2.B 3.A 4.C 5.D 二、计算题(每小题9分,共27分) 17 6.ABT= 0 1 3分 01-2 A1 0 -B-3 9分 7.y=(x3+2)'·e2+(x3+2)·(e)'=3x2e+(x3+2)·e*=(x3+3x2+2)·e* 9分 8.j1+3x2+e)dz=(x+x+e)=e+9 9分 三、编程题(每小题9分,共27分) 9. 计算AI+BCT的MATLAB命令语句为: >>clear 1分 >>A=[01:11] 2分 >>B=[10;-12] 3分 >>C-[2-1;-12] 4分 >>AT=inv(A) 5分 >>SD=AT+B*C' 9分 10. >>clear >>syms x 1分 >>y=a*x log(9+sqrt(4+x2)); 5分 >>dy=diff(y,2) 9分 882
试卷代号 :2320 国家开放大学(中央广播电视大学 )2015 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考〉 2016 一、单项选择题{每小题 分,共 20 分) 1. C 2. B 3. A 二、计算题{每小题 分,共 27 分} 4. C 5. D :4-j 7.y'=(x3+2)'. ez +(x3+2). (e =3x (x + 2) • eZ = (x3 + 3x2 + 2) • eZ 8. f: (1 + 介的dx=(x+ 扑的 1: =e2 + 9 三、编程题{每小题 分,共 27 分} 计算 A-1+BC MATLAB 命令语句为 >>clear >>A=[O 1;1 1J >>B=[l 0;-1 2J >>C=[2 -1;-1 2J >>AT=inv(A) >>SD=AT+B C' 10. >>clear >>syms x >>y=a^x og(9+sqrt(4+x^2)) ; > >dy=diff(y,2) 882
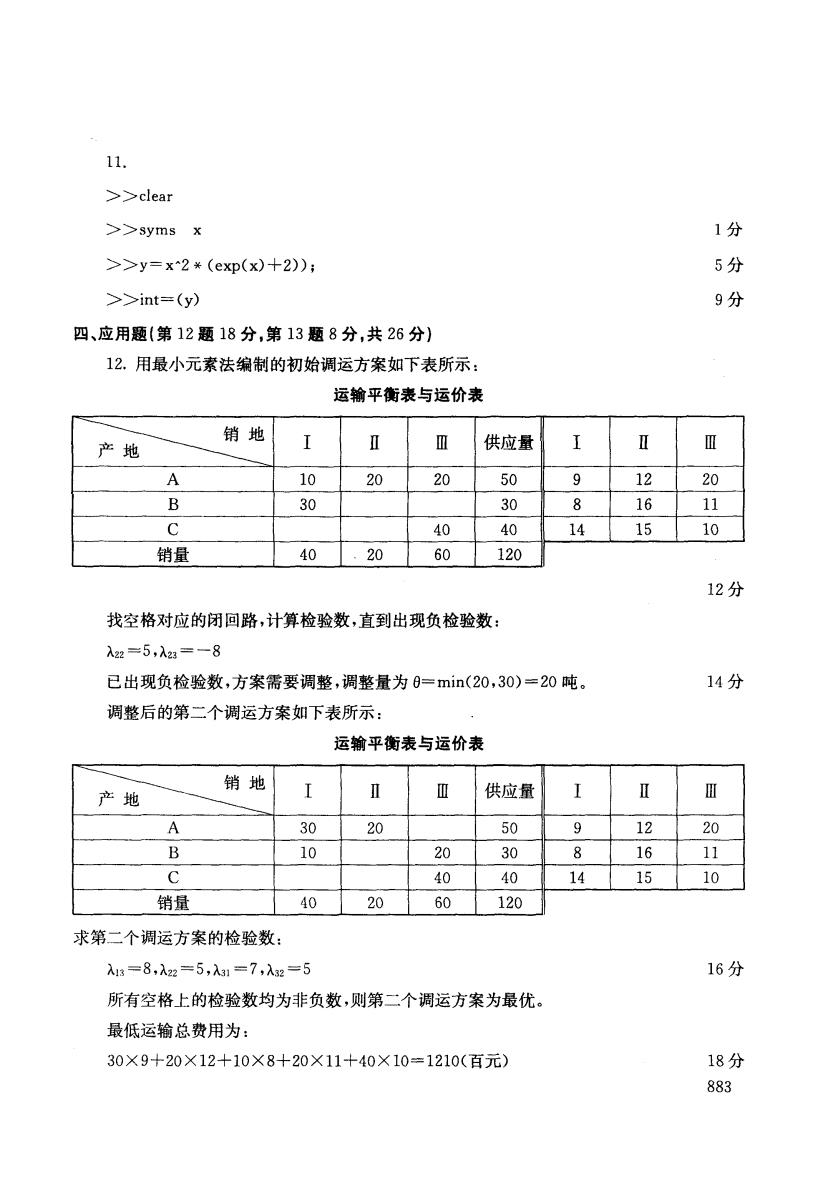
11. >>clear syms x 1分 >>y=x2¥(exp(x)+2)); 5分 >>int=(y) 9分 四、应用题(第12题18分,第13题8分,共26分) 12.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 产地 I Ⅱ Ⅲ 供应量 I Ⅱ Ⅲ A 10 20 20 50 9 12 20 B 30 30 8 16 11 C 40 40 14 15 10 销量 40 20 60 120 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: 入22=5,λ23=-8 已出现负检验数,方案需要调整,调整量为0=min(20,30)=20吨。 14分 调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 产地 I Ⅲ 供应量 I I Ⅲ A 30 20 50 9 12 20 B 10 20 30 8 16 11 C 40 40 14 15 10 销量 40 20 60 120 求第二个调运方案的检验数: 入13=8,入22=5,入31=7,入32=5 16分 所有空格上的检验数均为非负数,则第二个调运方案为最优。 最低运输总费用为: 30×9+20×12+10×8+20×11-+40×10=1210(百元) 18分 883
11. >>clear >>y=x^2 (exp(x) 2)); >>int=(y) >>syms x 囚、应用题{第 12 18 分,第 13 分,共 26 分) 12. 用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 豆\\芝? I E 供应量 I H A 10 20 20 50 9 12 20 B 30 30 8 16 11 C 40 40 14 15 10 销量 40 20 60 120 」一一 」一 12 找空格对应的闭回路,计算检验数,直到出现负检验数: 22 =5 ,À23 =-8 已出现负检验数,方案需要调整,调整量为 B=mín(20 30)=20 吨。 调整后的第二个调运方案如下表所示: 运输平衡表与运价衰 14 产\地飞飞飞飞\\销\ I H E 供应量 I E A 30 20 50 9 12 20 B 10 20 30 8 16 11 C 40 40 14 15 10 销量 40 20 60 120 求第二个调运方案的检验数: 13=8 À22=5 ,入31 =7 λ32=5 16 所有空格上的检验数均为非负数,则第二个调运方案为最优。 最低运输总费用为: 30X9 20X12 10X8 20X11 40X 10=1210( 百元) 18 883

13.设生产甲、乙、丙的产品产量分别为x吨、y吨和z吨,显然x,y,之≥0。 1分 maxS=3x+5y+4z [4x+5y+6z≤180 线性规划模型为:2x十3y十5x≤200 4分 x,y,z≥0 计算该线性规划模型的MATLAB语句为: >>clear; >>C=-[354] >>G=[456;235] 6分 >>H=[180200]' >>LB=[000]' 7分 >>[X,fval]=linprog(C,G,H,[],],LB) 8分 884
13. 设生产甲、乙、丙的产品产量分别为 吨、 吨和 吨,显然 二三 maxS=3x+5y 4z rl!IId--llt 49u ZZ ++- 53: YYJ ++WM -BAnk" nunu 计算该线性规划模型的 MATLAB 语句为 >>clear; >>c= [3 5 4J >>G=[4 5 6;2 3 5J >>H=[180 200J' >>LB=[O 0 OJ' > >[X,fvalJ=linprog(C ,G, ,口,口, LB) 884