
试卷代号:2320 座位■ 国家开放大学(中央广播电视大学)2015年春季学期“开放专科”期末考试 物流管理定量分析方法 试题 2015年7月 题号 二 三 四 总分 分 数 导数基本公式: (1)(c)'=0(c为常数) (2)(x)'=r1(a为常数) (3)(e)'=e (4)(a)'=alna(a>0,a≠1) (5)(lnx)'=1 (6)(1og.xy=l(a>0,a≠1) xlna 积分的基本公式: (I)∫d=x+c 。十7x+ca≠-1D (2)∫xdx= (3)[e'dz=e+c 4)∫ar*=aa*+c(a>0,a≠) 5)∫女=nlz+c MATLAB的常用标准函数表 函数 功能 abs(x) 绝对值函数,即x log(x) 以e=2.71828…为底的对数函数,即自然对数lnx log10(x) 以10为底的对数函数,即常用对数1gx xa a次方的幂函数,即x° sqrt(x) x的开平方根函数,即√元 a'x 以a为底的指数函数,即a exp(x) 以e为底的指数函数,即e 1036
试卷代号 :2320 座位号 国家开放大学(中央广播电视大学)2015 年春季学期"开放专科"期末考试 物流管理定量分析方法 试题 2015 导数基本公式 (1) (c)' =O(c 为常数〉 (3) (e =eZ (5) Onx) , =.l z (2) (x.)' x.- 1 为常数〉 (4) (α '=a"lna(a> 手1) (6) 吼叫'=J (a> 叫1) xma 积分的基本公式 (忖由 =x+c (2 lfdz=-i-zM+c(α#--1) J α+1 xdx=e +c (的 raIdx= ,L +c(a > 手1) J ma tdz=l I+c MATLAB 的常用标准函数表 abs(x) 绝对值函数,即 Ixl log(x) e=2.71828 …为底的对数函数,即自然对数 lnx log10(x) 10 为底的对数函数,即常用对数 19x x.a 次方的幕画数,即 sqrt(x) 的开平方根函数,即 rx ax 为底的指数函数,即 exp(x) 为底的指数画数,即 1036

得分 评卷人 一、单项选择题(每小题4分,共20分】 1.若某物资的总供应量小于总需求量,可增设一个( ),其供应量取总供应量与总需 求量的差额,并取该产地到各销地的单位运价为0,可将将供不应求运输问题化为供求平衡运 输问题。 A.虚产地 B.需求量 C.虚销地 D.供应量 2.某物流企业用甲、乙两种原材料生产A,B,C三种产品。企业现有甲原料50吨,乙原 料60吨。已知每吨A产品需要甲原料2吨;每吨B产品需要甲原料1吨,乙原料3吨;每吨C 产品需要甲原料0.5吨、乙原料1吨。又知每吨A,B,C产品的利润分别为3万元、2万元和1 万元。为列出获得最大利润的线性规划模型,设生产A,B,C三种产品的产量分别为x吨、y 吨和z吨,则甲原料的限制条件为()。 A.3y+x≤50 B.3x+2y十z≤50 C.2x+y+0.5z≤50 D.2x+y+0.5z>50 5 6 5 9并且A=B,则x=( 6 3.设A= ,B= )。 6-x9 9 A.1 B.2 C.3 D.4 4.设某公司运输某物品的总成本(单位:万元)函数为C(q)=1000+20g十g,则运输量为 100单位时的边际成本为( )万元。 A.1100 B.220 C.13000 D.3100 5.已知运输某物品q吨的边际成本函数(单位:元/吨)为MC(q)=100+10q,则运输该物 品从100吨到110吨时成本的增加量为()。 100 A. (100+10q)dg (100+2q)dg 11 10 110 C.MC(q)dg+C(o) D. (100+10g)dg 100 100 1037
|得分|评卷人 | 一、单项选择题{每小题 分,共 20 分} 1.若某物资的总供应量小于总需求量,可增设一个( ),其供应量取总供应量与总需 求量的差额,并取该产地到各销地的单位运价为 ,可将将供不应求运输问题化为供求平衡运 输问题。 A. 虚产地 C. 虚销地 B. 需求量 D. 供应量 2. 某物流企业用甲、乙两种原材料生产 三种产品。企业现有甲原料 50 吨,乙原 60 吨。已知每吨 产品需要甲原料 吨;每吨 产品需要甲原料 吨,乙原料 吨;每吨 产品需要甲原料 0.5 吨、乙原料 吨。又知每吨 产品的利润分别为 万元、 万元和 万元。为列出获得最大利润的线性规划模型,设生产 三种产品的产量分别为 吨、 吨和 吨,则甲原料的限制条件为( )。 A. 3y+z 50 C. 2x+y+0. 5z~50 B. 3x 2y z~二 50 D. 2x+y+0.5z>50 A B z 5k B FOny Z 5- qa A A.1 B.2 C.3 D.4 4. 设某公司运输某物品的总成本(单位 万元)函数为 C(q) = 1000+20q+ 矿,则运输量为 100 单位时的边际成本为( )万元。 A. 1100 C. 13000 B. 220 D. 3100 5. 已知运输某物品 吨的边际成本函数(单位 :5G/ 吨)为 MC(q) =100+10q 则运输该物 品从 100 吨到 110 吨时成本的增加量为( nu AC OM OC hurt tiEI dC J(B. fOOO+2 D j:::(100+Wdq 1037

得 分 评卷人 二、计算题(每小题7分,共21分)】 0 -1 6.已知矩阵A= ]A+c 7.设y=x2(3十e),求:y 8.计算定积分:。(e+3x)d 得 分 评卷人 三、编程题(每小题6分,共12分) 9.试写出用MATLAB软件计算函数y=(e+2)lnx的二阶导数的命令语句。 10.试写出用MATLAB软件计算定积分e(x+VG)dz的偷令语句. 得 分 评卷人 四、应用题(第11、12题各14分,第13题19分,共47分) 11.设某商品的价格p(万元/百台)与需求量q(百台)的关系是q=100一5p,求获最大收 入时的销量及最大收人。 12.某企业计划生产甲、乙两种产品,需要用A,B,C三种不同的原料。已知产品的生产 工艺如下:每生产一吨产品甲,需用A,B,C三种原料分别为1、1、2(吨);生产一吨产品乙,需 用三种原料分别为1、2、1(吨)。每天原料供应的能力分别为7、9、8(吨)。又知,销售一吨产品 甲,企业可得利润6万元;销售一吨产品乙,企业可得利润5万元。试建立使企业能获得最大 利润的线性规划模型,并写出用MATLAB软件计算该线性规划问题的命令语句。 13.某企业从A1,A2和A,三个产地,运送一批物资到B1,B2和B,三个销地。已知各产 地的供应量(单位:百吨)、各销地的需求量(单位:百吨)及各产地到各销地的单位运价(单位: 元/吨)如下表所示: 1038
|得分|评卷人| | 二、计算题{每小题 分,共 21 分} 已知矩阵 A~ ~ :]• A B C 'i Z JU {z FYK |得分|评卷人| | 三、编程题{每小题 分,共 12 分} 9. 试写出用 MATLAB 软件计算函数 y= (e +2)}nx 的二阶导数的命令语句。 10 试写出用 MATLAB 软件计算定积分s: 叫+../x灿的命令语句。 |得分|评卷人| | 四、应用题{第 11 12 题备 14 分,第 13 19 分,共 47 分} 1.设某商品的价格 ρ( 万元/百台〉与需求量 q( 百台〉的关系是 q=100 一句,求获最大收 ‘人时的销量及最大收入。 12. 某企业计划生产甲、乙两种产品,需要用 三种不同的原料。已知产品的生产 工艺如下 每生产一吨产品甲,需用 三种原料分别为 2( 吨) ;生产一吨产品乙,需 用三种原料分别为 、l(吨)。每天原料供应的能力分别为 、民吨〉。又知,销售一吨产品 甲,企业可得利润 万元 销售一吨产品乙,企业可得利润 万元。试建立使企业能获得最大 利润的线性规划模型,并写出用 MATLAB 软件计算该线性规划问题的命令语句。 13. 某企业从 Al A2 A3 三个产地,运送一批物资到矶 B2 和良三个销地。已知各产 地的供应量(单位 百吨〉、各销地的需求量(单位 百吨〉及各产地到各销地的单位运价(单位 元/吨〉如下表所示: 1038
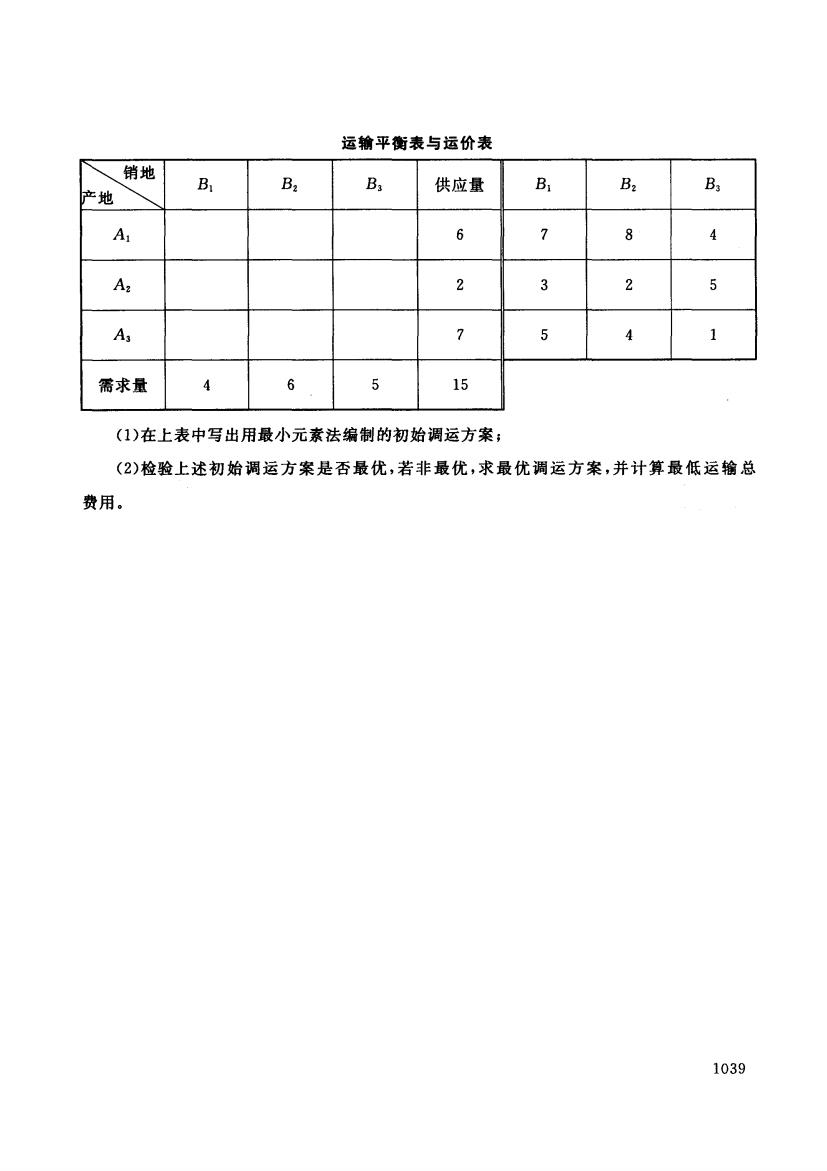
运输平衡表与运价表 销地 B Ba Ba 供应量 B, B2 Ba 产地 Ar 6 2 A: 2 3 2 5 A3 7 5 4 1 需求量 4 6 5 15 (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 1039
运输平衡表与运价表 斗可 Bl B2 B3 供应量 Bl B2 B3 Al 6 7 8 4 A2 2 3 2 5 A3 7 5 4 1 需求量 4 6 5 15 (1)在上表中写出用最小元素法编制的初始调运方案 (2) 检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 1039

试卷代号:2320 国家开放大学(中央广播电视大学)2015年春季学期“开放专科”期末考试 物流管理定量分析方法试题答案及评分标准 (供参考) 2015年7月 一、单项选择题(每小题4分,共20分)】 1.A 2.C 3.B 4.B 5.D 二、计算题(每小题7分,共21分) 2分 -[18 5分 7分 7.y=(x2)'。(3+e)+x2·(3+e)' 4分 =(2x)·(3+e2)+x2·e 7分 8.J(e+3x)dx =(e+x)=(e+1)-(e+o)=e 7分 三、编程题(每小题6分,共12分) 9.>>>clear >>syms x 2分 >>y=(exp(x)+2)*log(x); 4分 >>dy=diff(y,2) 6分 1040
试卷代号 :2320 国家开放大学(中央广播电视大学 )2015 年春季学期"开放专科"期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考) 2015 一、单项选择题(每小题 分,共 20 分} l. A 2.C 3. B 4. B 5.D 二、计算题{每小题 分,共 21 分} n--u + 'l ''··nru 1i -1 --2-2 4LBqdp FO A B + C 7. y'=(x2 )' • (3 ) + x 2 • (3 + eZ ) , = (2x) • (3 + eZ ) + x 2 • eZ 8. J: (er dx =(叶叫归 +1)一"。十 0) =e 三、编程题{每小题 分,共 12 分} 9. >>clear >>syms x >>y=(exp(x)+2) log(x) ; >>dy=diff句, 2) 1040

10.>>clear >>syms x 2分 >>y=exp(x)*(x2+sqrt(x)); 4分 >>int(y,0,1) 6分 四、应用题(第11、12题各14分,第13题19分,共47分) 11.解:由g=100-5p得p=20-0.2g 3分 收入函数为:R(q)=pg=(20-0.2q)q=20g-0.2g2 7分 求导数得:MR(q)=20-0.4g 令MR(g)=0,得唯一驻点q=50(百台) 13分 故,获最大收入时的销量是50百台,最大收入是: R(50)=20×50-0.2×502=500(万元) 14分 12.解:设生产甲、乙两种产品产量分别为x、y吨,显然,x、y≥0。 1分 maxS=6x+5y [x十y≤7 x+2y≤9 线性规划模型为: 8分 2x+y≥0 x,y≥0 计算该线性规划模型的MATLAB语句为: >>clear >>C=-[-65]:(或C=-[65]) >>G=[11:12:21]; 10分 >>H=[798]';(或>>H=[7;9;8];) >>LB=[00]';(或>>LB=[00];) 12分 >>X,fval]=linprog(C,G,H,[],]LB) 14分 1041
10. >>clear >>syms x >>y=exp(x) (x-2+sqrt(x)) ; >>int(y,O,l) 四、应用题{第 11 12 题各 14 分,第 13 19 分,共 47 分} 1.解 q=100-5 p=20-0.2q 收入函数为 :R(q)= q=(20 0.2q)q=20q 0.2l 求导数得 :MR(q)=20 0.4q MR(q)=O 得唯一驻点 q=50( 百台〉 13 故,获最大收入时的销量是 50 百台,最大收入是 R(50)=20X50 0.2X50 =500( 万元) 14 12. 设生产甲、乙两种产品产量分别为 吨,显然 maxS=6x 5y x+yζ7 x+2yζ9 线性规划模型为 2x+y注。 二三O 计算该线性规划模型的 MATLAB 语句为 >>clear >>c= [-6 5J 刊或 c= [6 5J) >>G=[l 1;1 2;2 1J; >>H=[7 9 8J';( >>H=[7; 9; 8J;) >>LB=[O OJ';( >>LB=[O OJρ 10 > >[X,fvalJ=linprog(C ,G , H. 口,口, LB) 12 14 1041
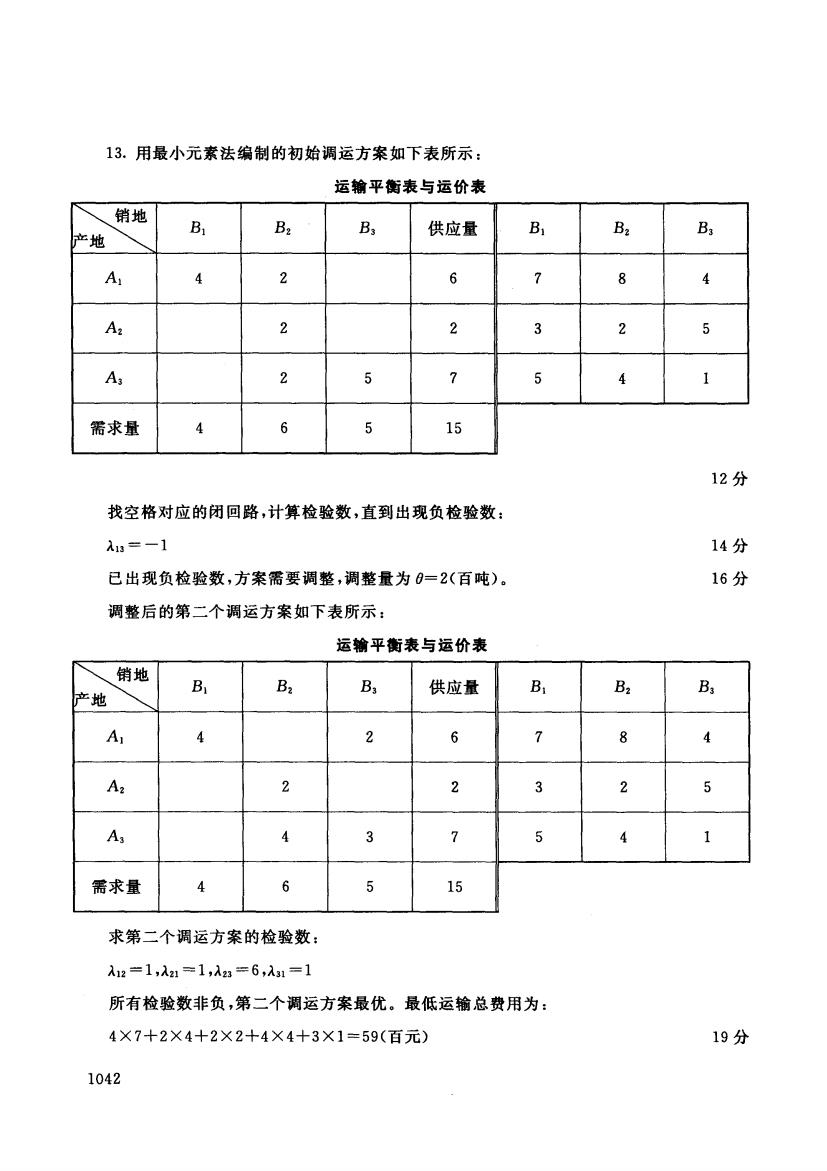
13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 B B2 B3 供应量 B B2 产地 A 2 6 7 8 A2 2 2 3 2 5 A3 2 5 7 5 4 1 需求量 4 6 5 15 12分 找空格对应的闭回路,计算检验数,直到出现负检验数: 入3=-1 14分 已出现负检验数,方案需要调整,调整量为0=2(百吨)。 16分 调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 B Ba 供应量 Bi B2 B 产地 B2 A 4 2 6 7 8 A2 2 2 3 2 5 A3 4 3 7 5 4 1 需求量 6 5 15 求第二个调运方案的检验数: 入12=1,λ21=1,λ23=6,λ31=1 所有检验数非负,第二个调运方案最优。最低运输总费用为: 4×7+2×4+2×2+4×4+3×1=59(百元) 19分 1042
13. 用最小元素法编制的初始调运方案如下表所示 运输平衡表与运价衰 年吧 BI B2 B3 供应量 AI 4 2 6 A 2 2 2 A3 2 5 7 需求量 4 6 5 15 L..-. --'-- 找空格对应的闭回路,计算检验数,直到出现负检验数 λ13=-1 已出现负检验数,方案需要调整,调整量为 8=2( 百吨)。 调整后的第二个调运方案如下表所示 运输平衡表与运价囊 比吧 BI B2 B3 供应量 AI 4 2 6 A 2 2 2 A3 4 3 7 需求量 4 6 5 15 求第二个调运方案的检验数 λ12=1 λ21 = 1 "l23 = 6 λ31 =1 BI 7 3 5 BI 7 3 5 所有检验数非负,第二个调运方案最优。最低运输总费用为= 4X7 X4+2 X2+4 X4+3 X 1 =59( 百元〉 1042 B2 8 2 4 B2 8 2 4 B3 4 5 I 12 14 16 B3 4 5 1 19