
试卷代号:2320 座位号 国家开放大学(中央广播电视大学)2014年秋季学期“开放专科”期末考试 物流管理定量分析方法试题 2015年1月 题号 二 三 四 总分 双 数 导数基本公式: (1)(c)'=0(c为常数) (2)(x)'=x-1(a为常数) (3)(e2)'=e' (4)(a)'=a*lna(a>0,a≠1) (5)nx)e (6)1og.xy=1(a>0,a≠1) xlna 积分的基本公式: (a)∫dx=x+c 2小。xn+ca≠-1D (3)e'dr=e*+c ④jard=品+ca>0,a≠) 6)∫dr=lalx+c MATLAB的常用标准函数表 函数 功 能 abs(x) 绝对值函数,即|x log(x) 以e=2.71828…为底的对数函数,即自然对数lnx log10(x) 以10为底的对数函数,即常用对数1gx x'a a次方的幂函数,即x sqrt(x) x的开平方根函数,即√红 a'x 以a为底的指数函数,即a exp(x) 以e为底的指数函数,即e 1117
试卷代号 :2320 座位号rn 国家开放大学(中央广播电视大学)2014 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题 2015 |题号|一| |分数 E 导数基本公式: (1) (c) =O(c 为常数) (3) (e) =e (2) (x.) ~X.-l (Q'为常数) (4) (aX) =axlna(a > 手1) (5) C1nx) , = ~ z (6) Clogax)' (α>0 ,叫1) xlna 积分的基本公式: dx=x (2)jfdz=trvc叶1) (3) xdx= (4) I aXdx 士于~aX +c(a > α* 1) J lna tdz=MZ|+c MATLAB 的常用标准函数表 abs(x) 绝对值函数,即 Ixl log(x) e=2.71828 …为底的对数函数,即自然对数 lnx log10(x) 10 为底的对数函数,即常用对数 19x x^a 次方的事函数,即 sqrt( x) 的开平方根函数,即 rx a^x 为底的指数函数,即 exp(x) 为底的指数函数,即 1117

得分 评卷人 一、单项选择题(每小题4分,共20分) 1.若某物资的总供应量小于总需求量,可增设一个(),其供应量取总需求量与总供 应量的差额,并取该产地到各销地的单位运价为0,则可将供不应求运输问题化为供求平衡运 输问题。 A.虚销地 B.虚产地 C.需求量 D.供应量 2.某物流公司有三种化学原料A1,A2,A3。每公斤原料A1含B1,B2,B,三种化学成分的含 量分别为0.7公斤、0.2公斤和0.1公斤:每公斤原料A2含B1,B2,B的含量分别为0.1公斤、0.3 公斤和0.6公斤:每公斤原料A含B,,B2,B,的含量分别为0.3公斤、0.4公斤和0.3公斤。每 公斤原料A1,A2,A:的成本分别为500元、300元和400元。今需要B,成分至少100公斤,B2成 分至少50公斤,B成分至少80公斤。为列出使总成本最小的线性规划模型,设原料A1,A2,A 的用量分别为x公斤、x公斤和x3公斤,则化学成分B2应满足的约束条件为()。 A.0.2x1+0.3x2+0.4x3≥50 B.0.2x1+0.3x2+0.4x3≤50 C.0.2x1+0.3x2+0.4x3=50 D.0.2x1+0.3x2+0.4xa>50 1 2 2 10 3.设A= 6 ,B= 则计算AT+3B的MATLAB语句为()。 3 -5 1-3 4 A.AT+3B B.AT+3¥B C.A'+3B D.A’+3*B 4.设某公司运输某物品的总成本(单位:百元)函数为C(q)=q2+50q+4000,则运输量为 100单位时的总成本为()百元。 A.1900 B.190 C.19000 D.250 5.已知运输某物品q吨的边际收人函数(单位:元/吨)为MR(g)一100一3q,则运输该物 品从100吨到200吨时收入的增加量为()。 f200 A. (100-3q)dq B. J100 [(100-3q)dq J200 200 C.(100-3g)dg D. ,(3g-100)dg 10 1118
|得分|评卷人| | 一、单项选择题{每小题 分,共 20 分) 1.若某物资的总供应量小于总需求量,可增设一个( ) ,其供应量取总需求量与总供 应量的差额,并取该产地到各销地的单位运价为 ,则可将供不应求运输问题化为供求平衡运 输问题。 A. 虚销地 c.需求量 B. 虚产地 D. 供应量 2. 某物流公司有三种化学原料 AI' A3o 每公斤原料 AI 含乱,鸟,且三种化学成分的含 量分别为 0.7 公斤、 0.2 公斤和 O. 公斤;每公斤原料 Az 含且,鸟,且的含量分别为 0.1 公斤、0.3 公斤和 0.6 公斤;每公斤原料 含矶,鸟,队的含量分别为 0.3 公斤、 0.4 公斤和 0.3 公斤。每 公斤原料 AI' A3 的成本分别为 500 元、 300 元和 400 元。今需要 BI 成分至少 100 公斤, Bz 分至少 50 公斤,且成分至少 80 公斤。为列出使总成本最小的线性规划模型,设原料 /\1 ,儿 A3 的用量分别为 XI 公斤、工 公斤和工 公斤,则化学成分 Bz 应满足的约束条件为)。 A. O. 2xI +0. 3xz +0. 4X3 二三 50 c. O. 2xI +0. 3xz +0. =50 B. O. 2xI +0. 3X2 0. 4X 350 •• -3 --if--iL B 9'unbAq A 101 ,则计算 AI 3B MATLAB 语句为( 4 1 A. AT +3B C. A'+3B B. A T +3 D. A' 4. 设某公司运输某物品的总成本(单位:百元)函数为 CCq)= 旷十 50q+4000 则运输量为 100 单位时的总成本为( )百元。 A. 1900 C. 19000 B. 190 D. 250 5. 己知运输某物品 吨的边际收入函数(单位:元/吨)为 MR(q)=100 一句,则运输该物 品从 100 吨到 200 吨时收入的增加量为( A jp100 一刷 B j ;;;〉〉::二川〉:〉〉〉(门 α10贮)( D j:::(3q QA IG q TEA AU AU "'-EEBB-'jU C 1118

得分 评卷人 二、计算题(每小题7分,共21分) ① -1 01 203 6.已知矩阵A=0 1 -2,B= ,求:BA 01-1 3 0 2 7.设y=2十,求:y 8.计算定积分:(c-r)d 得分 评卷人 三、编程题(每小题6分,共12分) 9.试写出用MATLAB软件计算函数y=ln(x十√1+x2)的导数的命令语句。 10.试写出用MATLAB软件计算定积分,Izle'dr的命令语句. 得分 评卷人 四、应用题(第11、12题各14分,第13题19分,共47分) 11.运输某物品q百台的成本(单位:万元)函数为C(q)一40gq+300,收入(单位:万元)函 数为R(q)=100q一q,问运输量为多少时利润最大?最大利润是多少? 12.某物流公司经过对近期销售资料分析及市场预测得知,该公司生产的甲、乙、丙三种 产品,均为市场紧俏产品,销售量一直持续上升、经久不衰。今已知上述三种产品的单位产品 原材料消耗定额分别为4公斤、4公斤和5公斤:三种产品的单位产品所需工时分别为6台 时、3台时和6台时。另外,三种产品的利润分别为400元/件,250元/件和300元/件。由于 生产该三种产品的原材料和工时的供应有一定限制,原材料每天只能供应180公斤,工时每天 只有150台时。试建立能获得最大利润的线性规划模型,并写出用MATLAB软件计算该线 性规划模型的命令语句。 1119
二、计算题{每小题 分,共 21 分) A B A 1llil--J 7. ·百i~ Y=2+x v=~ 言,习求'<.:y 计算定积分 J: CC" - x)dx 三、编程题(每小题 分,共 12 分} 9. 试写出用 MATLAB 软件计算函数 y=ln(x 7) 的导数的命令语句。 10 试写出用 MATLAB 软件计算定积分[1 I x 巾的命令语句。 四、应用题(第 11 12 题各 14 分,第 13 19 分,共 17 分) 1.运输某物品 百台的成本(单位:万元)函数为 C(q)=10q 300 ,收入(单位:万元)函 数为 R(q)=100q_q2 问运输量为多少时利润最大?最大利润是多少? 12. 某物流公司经过对近期销售资料分析及市场预测得知,该公司生产的甲、乙、丙三种 产品,均为市场紧俏产品,销售量-直持续上升、经久不衰。今已知上述三种产品的单位产品 原材料消耗定额分别为 公斤 公斤和 公斤;三种产品的单位产品所需工时分别为 时、 台时和 台时。另外,三种产品的利润分别为 400 元/件、 250 元/件和 300 元/件。由于 生产该三种产品的原材料和工时的供应有」定限制,原材料每天只能供应 180 公斤,工时每天 只有 ]50 台时。试建立能获得最大利润的线性规划模型,并写出用 MATLAB 软件计算该线 性规划模型的命令语句。 1119
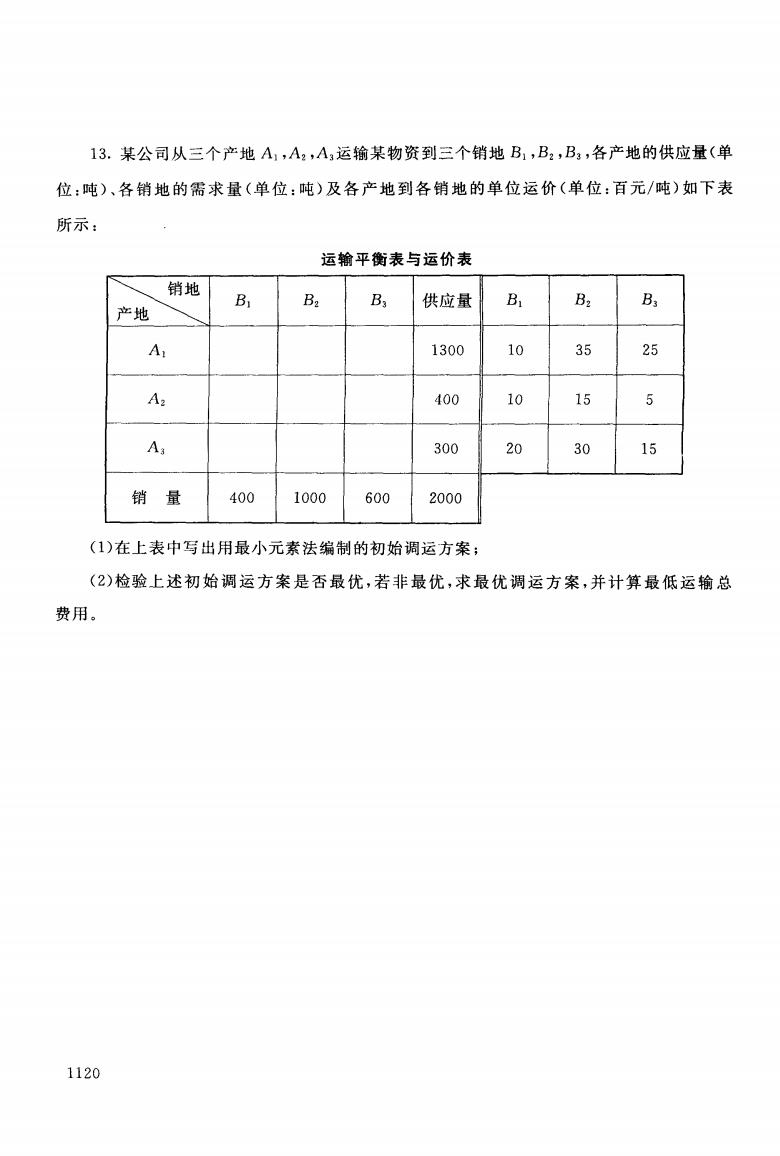
13.某公司从三个产地A1,A2,A3运输某物资到三个销地B1,B2,B,,各产地的供应量(单 位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 运输平衡表与运价表 销地 B B2 B B3 产地 B3 供应量 B2 A 1300 10 35 25 A2 400 10 15 5 A3 300 20 30 15 销量 400 1000 600 2000 (1)在上表中写出用最小元素法编制的初始调运方案; (2)检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 1120
13. 某公司从三个产地儿,儿,儿运输某物资到三个销地乱 B2 且,各产地的供应量(单 位:吨)、各销地的需求量(单位:吨)及各产地到各销地的单位运价(单位:百元/吨)如下表 所示: 运输平衡表与运价表 斗? Bl B2 B3 供应量 Bl B2 B3 Al 1300 10 35 25 A 2 400 10 15 5 A3 300 20 30 15 400 1000 600 2000 一一一 (1)在上表中写出用最小元素法编制的初始调运方案; (2) 检验上述初始调运方案是否最优,若非最优,求最优调运方案,并计算最低运输总 费用。 1120

试卷代号:2320 国家开放大学(中央广播电视大学)2014年秋季学期“开放专科”期未考试 物流管理定量分析方法试题答案及评分标准 (供参考) 2015年1月 一、单项选择题(每小题4分,共20分) 1.B 2.A 3.D 4.C 5.A 二、计算题(每小题7分,共21分)】 2 -1 0 20 3 13 6.BA= 0 -2 -26 7分 01-1 L-3 1-4 3 0 2 7.y=e)'·(2+x)-·(2+xy=2+x2-2x)e (2+x2)2 (2+x2)2 7分 &.(e-xdz=(e-2=e-2 7分 三、编程题(每小题6分,共12分) 9.>>clear >syms 2分 >>y=log(x+sqrt(1+x2)); 4分 >>dy=diff(y) 6分 10.>>clear >>syms x 2分 >>y=abs(x)exp(x); 4分 >>int(y,-1,3) 6分 四、应用题(第11、12题各14分,第13题19分,共47分) 11.利润函数L(q)=R(q)-C(q)=60g-g2-300 6分 1121
试卷代号 :2320 国家开放大学(中央广播电视大学 )2014 年秋季学期"开放专科"期末考试 物流管理定量分析方法 试题答案及评分标准 (供参考) 2015 一、单项选择题{每小题 分,共 20 分} l. B 2.A 3. D 4. C 5. A 二、计算题{每小题 分,共 21 分) ''qd qu p--MVLU -lo o-2 -- nuti 3- nhu B A 7. v'=~e )' • (2 - e . (2 + x 2)' 2+X2 2x)e J (2+ X2)2 (2 x2 )2 8. J:何一训 = (e 一护)|;=e-? 三、编程题(每小题 分,共 12 分) 9. >>clear >>syms x >>y=log(x sqrt (l十 x-2)) ; > >dy=diff(y) 10. >>clear >>syms x >>y=abs(x) exp(x); >>int(y ,一 3) 四、应用题(第 11 12 题各 14 分,第 13 19 分,共 47 分) 1.利润函数 L(q) =R(q) -C(q) =60q_q2 -300 1121

令边际利润ML(g)=60一2g=0,得惟一驻点q=30(百台) 11分 故当运输量为30百台时,利润最大。 12分 最大利润为L(30)=600(万元) 14分 12.设生产甲、乙、丙三种产品产量分别为x1件、x2件和x3件,显然,x1,x2,x3≥0。 1分 maxS=400.x1+250x2十300x [4x1+4x2+5x3≤180 线性规划模型为:6x1十3x2+6x3≤150 8分 x1,x2,x3≥0 计算该线性规划模型的MATLAB语句为: >>clear >>C=[-400-250-300]: >>A=[445;636] 10分 >>B=[180150]';(或>>B=[180150];) >>LB=[000]';(或>>LB=[000];) 12分 >X,fval]=linprog(C,A,B,[],[],LB) 14分 13.用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 销地 B 供应量 产地 B2 B B 33 A 400 900 1300 10 35 25 A2 400 400 10 15 13 100 200 300 20 30 15 销量 400 1000 600 2009 12分 找空格对应的闭回路,计算检验数,直到出现负检:: 1122
令边际利润 ML(q)=60-2q=0 得惟一驻点 q=30( 百台) 11 故当运输量为 30 百台时,利润最大。 12 最大利润为 (30) =600( 万元) 14 12. 设生产甲、乙、丙三种产品产量分别为工 件、工 件和工 件,显然,码, zz Z32 maxS=400Xl +250 300X3 (4Xl +4X2 5X 180 线性规划模型为:~ 6Xl +3X2 +6 3>clear >>C=[ -400 -250 -300J; >>A=>B=[180 150J';( >>B= [1 80 150Jρ >>LB=[O 0 OJ';( >>LB=[O 0 OJ;) > >[X ,fva!J= !inprog(C ,口,口, B) 10 12 14 13. 用最小元素法编制的初始调运方案如下表所示: 运输平衡表与运价表 B3 10 寸一二 T25 JL; 30077;-l 12 ] }j 1300 并吁: Bl B2 供应量 Al 400 900 八, 400 '/\3 100 200 销量 100 1000 AU O 12 找空格对应的闭回路,计算检验数,直到出现负拉 1:,' 1122

A13=5,A21=15,λ22=-5 14分 已出现负检验数,方案需要调整,调整量为0=100吨。 16分 调整后的第二个调运方案如下表所示: 运输平衡表与运价表 销地 B B2 供应量 B B 产地 B3 B2 Au 400 900 1300 10 35 25 A2 100 300 400 10 15 5 A, 300 300 20 30 15 销量 400 1000 600 2000 求第二个调运方案的检验数: λ13=0,入21=20,入31=20,入32=5 所有检验数非负,第二个调运方案最优。 最低运输总费用为: 400×10+900×35+100×15+300×5+300×15=43000(百元) 19分 1123
.1.\3 =5 λ21 = 15 λ22= -5 已出现负检验数,方案需要调整,调整量为 0=100 吨。 调整后的第二个调运方案如下表所示: 运输平衡表与运价表 斗呼 BI B2 B3 AI 400 900 A 2 100 300 A3 300 400 1000 600 求第二个调运方案的检验数 .1. 13 = 0 ,.1. 21 = 20 ,.1. 31 = 20 ,.1. 32 = 5 所有检验数非负,第二个调运方案最优。 最低运输总费用为: 供应量 1300 400 300 2000 BI 10 10 20 400 X 10+900X35+100X 15+300X 5+300X 15=4300QC 百元) B2 35 15 30 B3 25 5 15 14 16 19 1123