
第九章率失真函数
第九章 率失真函数

无失真信源编码和有噪信道编码告诉我们:只要信道的 信息传输速率小于信道容量,总能找到一种编码方法,使得 在该信道上的信息传输的差错概率任意小;反之,若信道 的信息传输速率大于信道容量,则不可能使信息传输差错 概率任意小。 问题:若信息速率大于信道容量,怎么办? 无失真的编码并非总是必要的。 引入失真,允许失真大,信息率可以越低。P248例
无失真信源编码和有噪信道编码告诉我们:只要信道的 信息传输速率小于信道容量,总能找到一种编码方法,使得 在该信道上的信息传输的差错概率任意小;反之,若信道 的信息传输速率大于信道容量,则不可能使信息传输差错 概率任意小。 问题:若信息速率大于信道容量,怎么办? 无失真的编码并非总是必要的。 引入失真,允许失真大,信息率可以越低。P248例

香农首先定义了信息率失真函数RD),并论述了关于这个 函数的基本定理。 定理指出:在允许一定失真度D的情况下,信源输出的信 息传输率可压缩到R(D)值,这就从理论上给出了信息传输率与 允许失真之间的关系,奠定了信息率失真理论的基础。 信息率失真理论是进行量化、数模转换、频带压缩和数据 压缩的理论基础。 本章主要介绍信息率失真理论的基本内容,侧重讨论离散 无记忆信源。 首先给出信源的失真度和信息率失真函数的定义与性质; 然后讨论离散信源和连续信源的信息率失真函数计算;在这基 础上论述保真度准测下的信源编码定理
香农首先定义了信息率失真函数R(D),并论述了关于这个 函数的基本定理。 定理指出:在允许一定失真度D的情况下,信源输出的信 息传输率可压缩到R(D)值,这就从理论上给出了信息传输率与 允许失真之间的关系,奠定了信息率失真理论的基础。 信息率失真理论是进行量化、数模转换、频带压缩和数据 压缩的理论基础。 本章主要介绍信息率失真理论的基本内容,侧重讨论离散 无记忆信源。 首先给出信源的失真度和信息率失真函数的定义与性质; 然后讨论离散信源和连续信源的信息率失真函数计算;在这基 础上论述保真度准则下的信源编码定理

失真测度 一、 失真度 ·从直观感觉可知,若允许失真越大,信息传输率可 越小;若允许失真越小,信息传输率需越大。 ·所以信息传输率与信源编码所引起的失真(或误差) 是有关的
失真测度 一、失真度 ⚫ 从直观感觉可知,若允许失真越大,信息传输率可 越小;若允许失真越小,信息传输率需越大。 ⚫ 所以信息传输率与信源编码所引起的失真(或误差) 是有关的

失真测度 离散无记忆信源U,信源变量U={u1,u2,u}, 概率分布为P(u)=[P(u),P(2).P(ur】。 信源符号通过信道传输到某接收端,接收端的 接收变量V=V1,V2,Vs}。 对应于每一对(u,V),我们指定一个非负的函数: 0 i=j d()= a(>0)i≠j 称为单个符号的失真度(或失真函数)。 通常较小的d值代表较小的失真,而d(uy)=0 表示没有失真
离散无记忆信源U,信源变量U={u1 ,u2 ,…ur }, 概率分布为P(u)=[P(u1 ),P(u2 ),…P(ur )] 。 信源符号通过信道传输到某接收端,接收端的 接收变量V= {v1 ,v2 ,…vs } 。 对应于每一对(u,v),我们指定一个非负的函数: 称为单个符号的失真度(或失真函数)。 通常较小的d值代表较小的失真,而d(ui ,vj)=0 表示没有失真。 i j i j d u v i j = = ( 0) 0 ( , ) 失真测度

失真矩阵D 若信源变量U有r个符号,接收变量V有s个符号, 则d(u,)就有r×s个,它可以排列成矩阵形式,即: d(41,y1)d(u1,y2).d(u1,yg) d42,1y)d(42,y2)… d(uz;v,) D= d(u,y)d(u,y2)…d(u,y) 它为失真矩阵D,是Xs阶矩阵
若信源变量U有r个符号,接收变量V有s个符号, 则d(ui ,vj )就有r×s个,它可以排列成矩阵形式,即: 它为失真矩阵D,是 r×s 阶矩阵。 = ( , ) ( , ) ... ( , ) : : ... : ( , ) ( , ) ... ( , ) ( , ) ( , ) ... ( , ) 1 2 2 1 2 2 2 1 1 1 2 1 r r r s s s d u v d u v d u v d u v d u v d u v d u v d u v d u v D 失真矩阵D
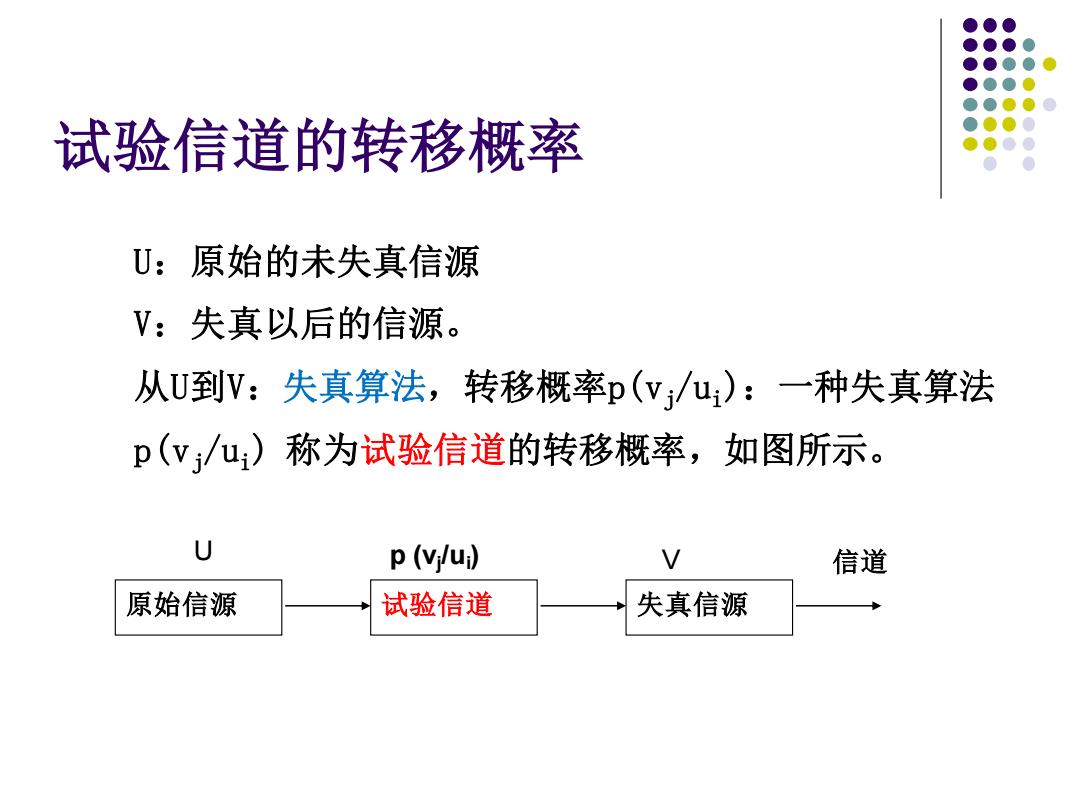
试验信道的转移概率 U:原始的未失真信源 V:失真以后的信源。 从U到V:失真算法,转移概率p(V/u):一种失真算法 p(vu:)称为试验信道的转移概率,如图所示。 U p (vj/u) V 信道 原始信源 试验信道 失真信源
U:原始的未失真信源 V:失真以后的信源。 从U到V:失真算法,转移概率p(vj/ui):一种失真算法 p(vj/ui) 称为试验信道的转移概率,如图所示。 原始信源 试验信道 失真信源 U p (vj /ui ) V 信道 试验信道的转移概率

[例1]离散对称信源(r=s)。信源变量U={u1,u2u}, 接收 量V={V1,V2,Vs}。定义单个符号失真度: u;=v d(4,y)= 1 u;丰V 这种失真称为汉明失真。汉明失真矩阵是一方阵,对角线上的 元素为零,即: 1 0 1 D 0 对二元对称信源(s=r=2),信源U={0,1},接收变量V={0,1}。在 汉明失真定义下,失真矩阵为:
[例1] 离散对称信源(r=s)。信源变量U={u1 ,u2 ,…ur } ,接收变 量V= {v1 ,v2 ,…vs }。定义单个符号失真度: 这种失真称为汉明失真。汉明失真矩阵是一方阵,对角线上的 元素为零,即: = = i j i j i j u v u v d u v 1 0 ( , ) r r D = 1 1 ... 0 : : ... : 1 0 ... 1 0 1 ... 1 • 对二元对称信源(s=r=2),信源U={0,1},接收变量V={0,1}。在 汉明失真定义下,失真矩阵为: = 1 0 0 1 D

[例2]删除信源。信源变量U={u1,u2,u},接收变量V牛 V1,V2,Vs}(s=r+1)。定义其单个符号失真度为: 0 i=j d(4,)=1 i≠ji 除=s以外所有的和 1/2 i=s 所有1 。其中接收符号Vs作为一个删除符号。 在这种情况下,意味着若把信源符号再现为删除符号Vs 时,其失真程度要比再现为其他接收符号的失真程度少 一半。 若二元删除信源s=2,r=3,U={0,1},V={0,1,2}。 失真度为: d(0,0)=d(1,2)=0 d(0,2)=d(1,0)=1 则 d(0,1)=d(1,1)=1/2 1 0 2
[例2] 删除信源。信源变量U={u1 ,u2 ,…ur } ,接收变量V= {v1 ,v2 ,…vs } (s = r+1) 。定义其单个符号失真度为: ⚫ 其中接收符号vs作为一个删除符号。 ⚫ 在这种情况下,意味着若把信源符号再现为删除符号vs 时,其失真程度要比再现为其他接收符号的失真程度少 一半。 ⚫ 若二元删除信源s =2,r=3, U={0,1},V={0,1 ,2} 。 失真度为: 则 = 0 2 1 1 1 2 1 0 D d(0,0)=d(1,2)=0 d(0,2)=d(1,0)=1 d(0,1)=d(1,1)=1/2 j s i j i j d u v i j = = = 1/ 2 1 0 ( , ) 除j=s以外所有的j和i 所有i

[例3]对称信源(s=r)。信源变量U={u1,u2,u},接收变 量V={V1,V2,Vs}。失真度定义为: d(4,yj)=(y,-4)2 若信源符号代表信源输出信号的幅度值,这就是一种以方 差表示的失真度。它意味着幅度差值大的要比幅度差值小的所 引起的失真更为严重,严重程度用平方来表示。 当r=3时,U={0,1,2},V={0,1,2},则失真矩阵为: 「01 4 D= 10 410 上述三个例子说明了具体失真度的定义。一般情况下根 据实际信源的失真,可以定义不同的失真和误差的度量。另 外还可以按其他标准,如引起的损失、风险、主观感觉上的 差别大小等来定义失真度d(u,v)
[例3] 对称信源(s = r) 。信源变量U={u1 ,u2 ,…ur } ,接收变 量V= {v1 ,v2 ,…vs } 。失真度定义为: 若信源符号代表信源输出信号的幅度值,这就是一种以方 差表示的失真度。它意味着幅度差值大的要比幅度差值小的所 引起的失真更为严重,严重程度用平方来表示。 当 r=3时, U={0,1,2},V={0,1,2} ,则失真矩阵为: 2 ( , ) ( ) i j j ui d u v = v − = 4 1 0 1 0 1 0 1 4 D 上述三个例子说明了具体失真度的定义。一般情况下根 据实际信源的失真,可以定义不同的失真和误差的度量。另 外还可以按其他标准,如引起的损失、风险、主观感觉上的 差别大小等来定义失真度d(u,v)