
State Key Laboratory of Integrated Services Networks 国家重点实验室 纠错码一原理与方法
State Key Laboratory of Integrated Services Networks 纠错码——原理与方法

国家重点实验室 有关事项 目的:、了解信道编码的作用与意义,,对信道编码 的研究方法和成菓有产泛的基本认识,孚会应用, 为进一步研究打下基础 以概念和物理意义为主,数学推导尽量放 。考核形式:论文/计算机仿真+开卷考试 参考书:“纠错码原理与方法”,王新梅,西安电 子科技大学出版社,高等学校教材;“差错控制编码 (第二版)”,Shu Lin,.Daniel J.Costello,机械工业出 版社,电子与电气工程丛书)
有关事项 目的:了解信道编码的作用与意义,对信道编码 的研究方法和成果有广泛的基本认识,学会应用, 为进一步研究打下基础 特点:以概念和物理意义为主,数学推导尽量放 到课外 考核形式:论文/计算机仿真+开卷考试 参考书: “纠错码——原理与方法”,王新梅,西安电 子科技大学出版社,高等学校教材; “差错控制编码 (第二版)”, Shu Lin,Daniel J.Costello, 机械工业出 版社,电子与电气工程丛书)

国家重点实验室 第1章 纠错码基本概念 什么是纠错码?为什么要引入纠错码?纠错码在 通信系统中起什么作用? 。如何实现纠错码? 。如何衡量纠错码的纠错能力及性能? 。纠错码的发展概况
第1章 纠错码基本概念 什么是纠错码?为什么要引入纠错码?纠错码在 通信系统中起什么作用? 如何实现纠错码? 如何衡量纠错码的纠错能力及性能? 纠错码的发展概况

State Key Laboratory of Integrated Services Networks 国家重点实验室 1.1纠错码的作用
State Key Laboratory of Integrated Services Networks 1.1 纠错码的作用

国家重点实验室 {S) {m {C) M调制器 信源 信源编码器 信道编码器 (写入单元) C,) (E} 信道 噪声源 (存贮媒质) (C) ⊙ {m} (R) 解调器 信宿 信源译码器 信道译码器 (读出单元) 数字通信系统模型
数字通信系统模型
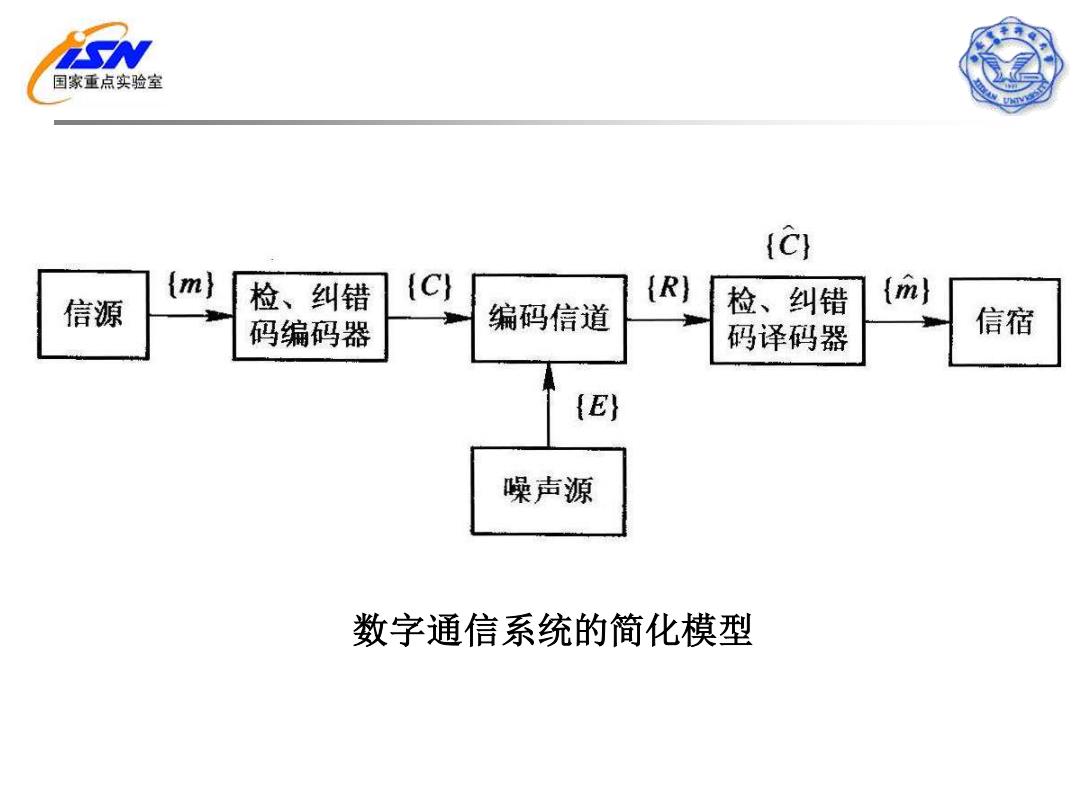
国家重点实验室 (C) {m} 检、纠错 {R) 检、纠错 (m) 信源 码编码器 编码信道 码译码器 信宿 {E} 噪声源 数字通信系统的简化模型
数字通信系统的简化模型

国家重点实验室 信源、信道与信道编码 信源:实时性与非实时性,可变速率,多媒体 。信道:离散与连续,时变与非时变,有记忆与无 记忆 >常见信道:模拟基带信道、射频信道、存储器等 。不同的信源和信道类型所对应的最佳编码方案是 不同的。 0 信道编码:从消息到信道波形或矢量的映射 复接、代数编码、调制、成形滤波、扩频、上下 变频等等都属于广义的信道编码范畴
信源、信道与信道编码 信源:实时性与非实时性,可变速率,多媒体 信道:离散与连续,时变与非时变,有记忆与无 记忆 ➢常见信道:模拟基带信道、射频信道、存储器等 不同的信源和信道类型所对应的最佳编码方案是 不同的。 信道编码:从消息到信道波形或矢量的映射 复接、代数编码、调制、成形滤波、扩频、上下 变频等等都属于广义的信道编码范畴

N 国家重点实验室 。信道编码:从消息到信道波形或矢量的映射 消息集中 信道波形 空间中的 失真后 恢复的 个元素 一个点 的波形 消息 信源 信道 信道 信道 信源 编码 编码 译码 译码 消息到波 判断是消 形的映射 引入失真 息集中的 哪个元素
信道编码:从消息到信道波形或矢量的映射 信 源 编 码 信 道 编 码 信 道 信 道 译 码 信 源 译 码 消息集中 一个元素 信道波形 空间中的 一个点 失真后 的波形 恢复的 消息 引入失真 消息到波 形的映射 判断是消 息集中的 哪个元素

国家重点实验室 信道 ®信道实际上也是从发空间X到收空间Y一 个映射函数 e发空间的维数n与收空间的维数m可以不 等 ©根据收发空间中每一维所取的数域有限 或无限可分为离散信道和连续信道 这里借用了空间的名称,但只用到了它 的集合概念而没有用到空间中的运算
信 道 信道实际上也是从发空间X到收空间Y一 个映射函数 发空间的维数n与收空间的维数m可以不 等 根据收发空间中每一维所取的数域有限 或无限可分为离散信道和连续信道 这里借用了空间的名称,但只用到了它 的集合概念而没有用到空间中的运算

国家重点实验室 信道特性的描述 e离散信道 >可用转移概率律描述:PO=bx=0), (a1,a2,.an)eX,b=(b1,b2,bm)∈Y,均为矢量 (或n(m)重符号)
信道特性的描述 离散信道 ➢可用转移概率律描述:P(y=b|x=a), a=(a1 ,a2 ,...an )X, b=(b1 ,b2 ,...bm)Y,均为矢量 (或n(m)重符号)