
第二章信息量和熵
第二章 信息量和熵

信息量和熵 ·离散变量的非平均信息量 。离散集的平均自信息量一熵 ·离散集的平均互信息量 ·信息不等式 ·凸函数和互信息的凸性 ·连续随机变量的互信息和微分熵
信息量和熵 ⚫ 离散变量的非平均信息量 ⚫ 离散集的平均自信息量-熵 ⚫ 离散集的平均互信息量 ⚫ 信息不等式 ⚫ 凸函数和互信息的凸性 ⚫ 连续随机变量的互信息和微分熵

2.1离散变量的非平均信 息量
2.1 离散变量的非平均信 息量

输入,输出空间定义 ●输入空间X-{xk=1,2,…,K),概率记为q(x) ● 输出空间Y={y-1,2,…J,概率记为ωy 联合空间XY={xyk=1,2,,K=1,2…,概率 为p(xy) p(x)=p(xklyi)@)=p(yilx)q(x)
输入,输出空间定义 ⚫ 输入空间X={xk ,k=1,2,…,K},概率记为q(xk ) ⚫ 输出空间Y={yj ,j=1,2,…,J},概率记为ω(yj ) ⚫ 联合空间XY={xk yj ;k=1,2,…,K;j=1,2,…,J}, 概率 为p(xk yj ) p(xk yj )= p(xk |yj )ω(yj )= p(yj |xk )q(xk )
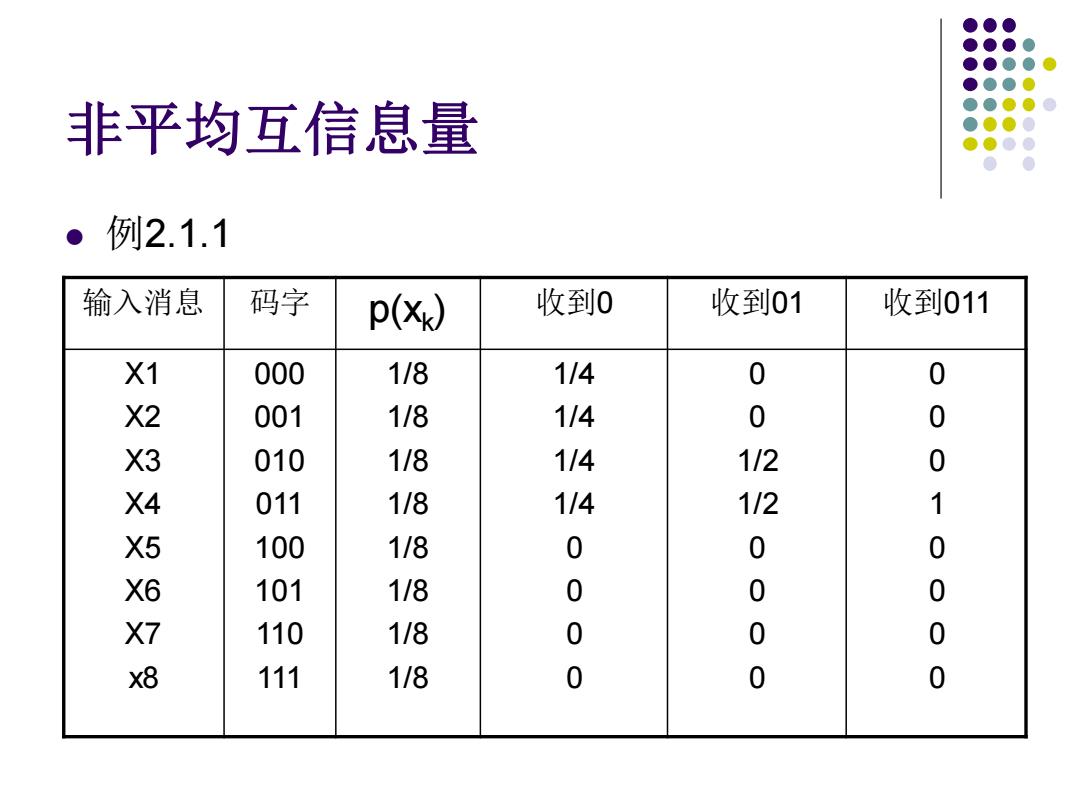
非平均互信息量 例2.1.1 输入消息 码字 p(xp) 收到0 收到01 收到011 X1 000 1/8 1/4 0 0 X2 001 1/8 1/4 0 0 X3 010 1/8 1/4 112 0 X4 011 1/8 1/4 1/2 1 X5 100 1/8 0 0 0 101 1/8 0 0 0 7 110 118 0 0 0 x8 111 1/8 0 0 0
非平均互信息量 ⚫ 例2.1.1 输入消息 码字 p(xk ) 收到0 收到01 收到011 X1 X2 X3 X4 X5 X6 X7 x8 000 001 010 011 100 101 110 111 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/8 1/4 1/4 1/4 1/4 0 0 0 0 0 0 1/2 1/2 0 0 0 0 0 0 0 1 0 0 0 0
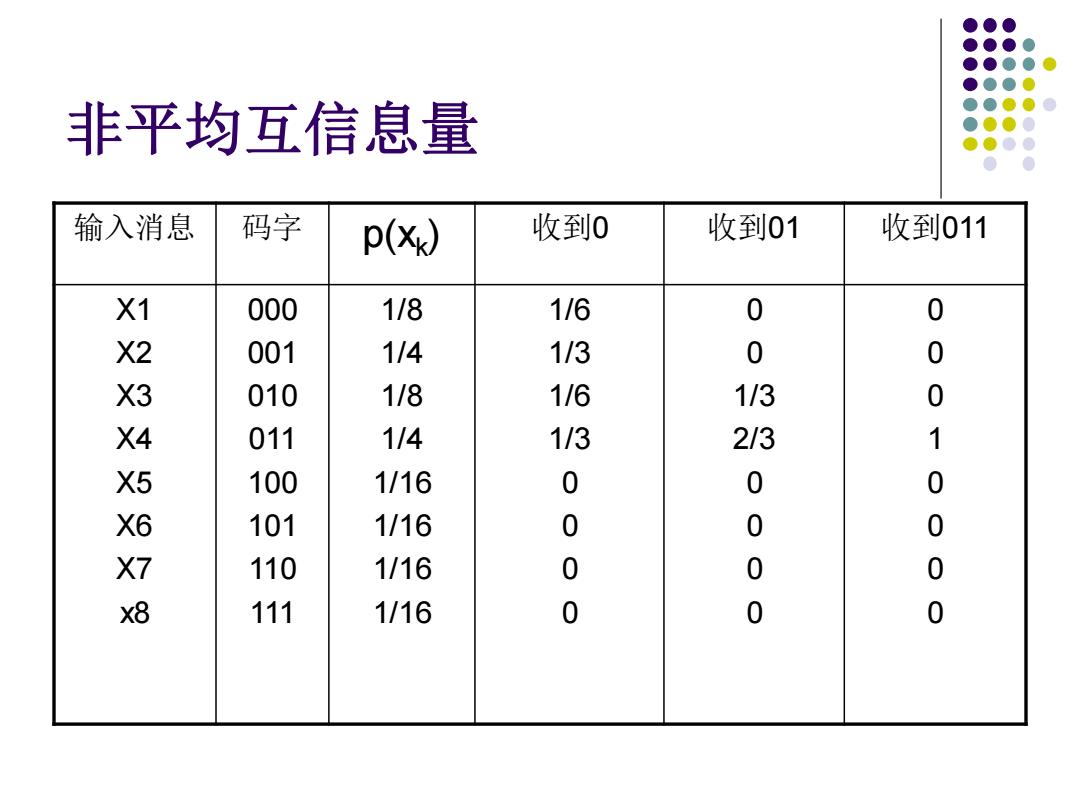
非平均互信息量 输入消息 码字 p(x) 收到0 收到01 收到011 X1 000 1/8 1/6 0 0 X2 001 1/4 1/3 0 0 X3 010 1/8 1/6 1/3 0 X4 011 1/4 113 2/3 1 X5 100 1/16 0 0 0 X6 101 1/16 0 0 0 X7 110 1/16 0 0 0 x8 111 1/16 0 0 0
非平均互信息量 输入消息 码字 p(xk ) 收到0 收到01 收到011 X1 X2 X3 X4 X5 X6 X7 x8 000 001 010 011 100 101 110 111 1/8 1/4 1/8 1/4 1/16 1/16 1/16 1/16 1/6 1/3 1/6 1/3 0 0 0 0 0 0 1/3 2/3 0 0 0 0 0 0 0 1 0 0 0 0
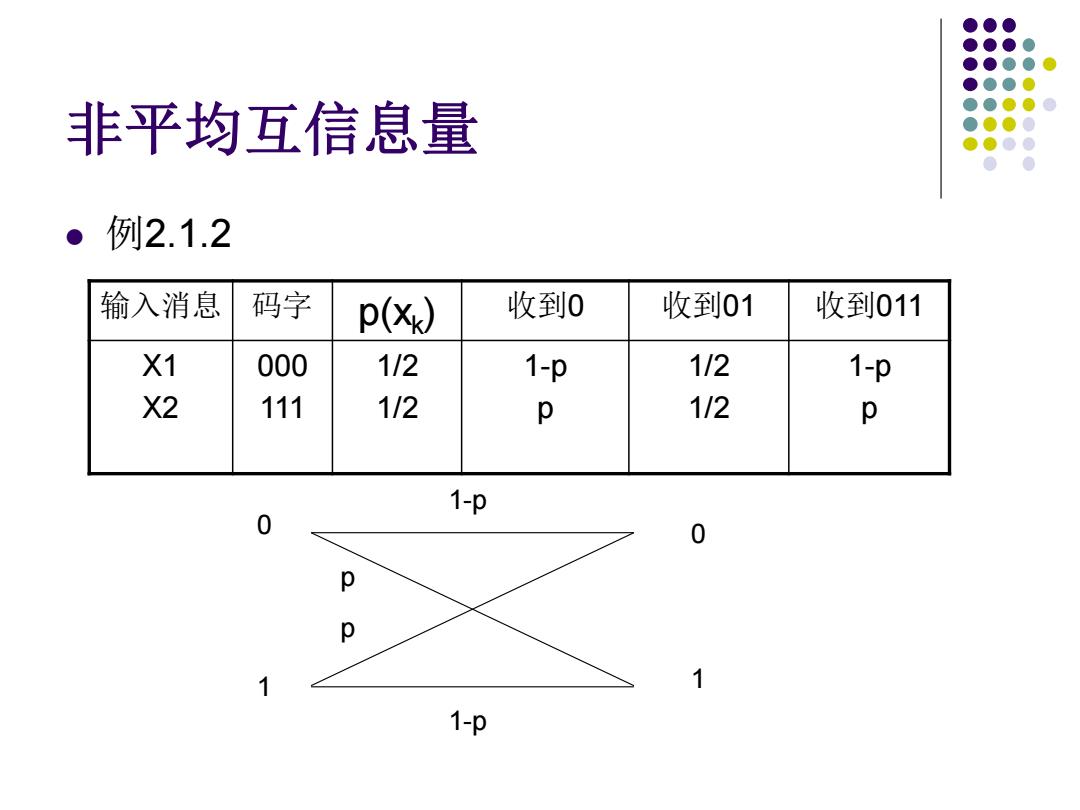
非平均互信息量 ● 例2.1.2 输入消息 码字 p(x) 收到0 收到01 收到011 X1 000 1/2 1-p 112 1-p X2 111 1/2 p 112 p 1-p 0 0 0 1 1 1-p
非平均互信息量 ⚫ 例2.1.2 输入消息 码字 p(xk ) 收到0 收到01 收到011 X1 X2 000 111 1/2 1/2 1-p p 1/2 1/2 1-p p 1-p 1-p 0 0 1 1 p p

非平均互信息量 I(xx;y;)=f(q(xx),p(xky)) I(y)=1xn)+1xiy) +I(xk;yi3 yiy)
非平均互信息量 ( ; ) ( ( ), ( | )) k j k k j I x y = f q x p x y ( ; | ) ( ; ) ( ; ) ( ; | ) 3 1 2 1 2 1 k j j j k j k j k j j I x y y y I x y I x y I x y y + = +

非平均互信息量 定义2.1.1(非平均互信息量)给定一个二维离 散型随机变量{(X,),(x),r,=1K, 1~乃(因此就给定了两个离散型随机变量 {X,xq-l~K和{Y,y,w广=1})。事件 x∈X与事件y,∈Y的互信息量定义为 1(x;y,)=l0ga P(X =x.IY=)=log. P(Y=yX=xx) P(X=xk) P(Y=y) -loga P((X,Y)=(xx,y)) P(X=x)P(Y=y) lo q:w
非平均互信息量 定义2.1.1(非平均互信息量) 给定一个二维离 散型随机变量{(X, Y), (xk , yj ), rkj, k=1~K; j=1~J}(因此就给定了两个离散型随机变量 {X, xk , qk , k=1~K}和{Y, yj , wj , j=1~J})。事件 xk∈X与事件yj∈Y的互信息量定义为 ( | ) ( | ) ( ; ) log log ( ) ( ) (( , ) ( , )) log log ( ) ( ) k j j k k j a a k j k j kj a a k j k j P X x Y y P Y y X x I x y P X x P Y y P X Y x y r P X x P Y y q w = = = = = = = = = = = = =

非平均互信息量 其中底数a是大于1的常数。常用a=2或a=e,当a=2 时互信息量的单位为“比特”。 几点说明: (1)Ick=loga(r/(qkw)。因此有对称性: IJy=I0y;k)。 (2) 当qkw,时I化k)=0。(当两个事件相互独 立时,互信息量为0)。 (3)当rqw,时Ick;>0,当qkw时Ick;y0。 (当两个事件正相关时,互信息量为正值,当两 个事件负相关时,互信息量为负值)
非平均互信息量 其中底数a是大于1的常数。常用a=2或a=e,当a=2 时互信息量的单位为“比特”。 几点说明: (1)I(xk ; yj )=loga (rkj/(qkwj ))。因此有对称性: I(xk ; yj )=I(yj ; xk )。 (2)当rkj=qkwj时I(xk ; yj )=0。(当两个事件相互独 立时,互信息量为0)。 (3)当rkj>qkwj时I(xk ; yj )>0,当rkj<qkwj时I(xk ; yj )<0。 (当两个事件正相关时,互信息量为正值,当两 个事件负相关时,互信息量为负值)