
第三章 信道 国家重点实验室 本章大纲 )、信道的定义、分类和模型 白)、恒参信道的传输特性及其对信号的影响 白、随参信道的传输煤质的三个特点,多径 传播对信号的影响 四、信道加性噪声的统计特性 、连续信道的信道容量(香农公式) 2011/11/13
第三章 信道 本章大纲 ㈠、信道的定义、分类和模型 ㈡、恒参信道的传输特性及其对信号的影响 ㈢、随参信道的传输媒质的三个特点,多径 传播对信号的影响 ㈣、信道加性噪声的统计特性 ㈤、连续信道的信道容量(香农公式) 2011/11/13 1

3.1、信道的定义与分类 1.狭义信道:仅指传输媒质。分为: ·有线信道(包括架空明线、对称电缆、同轴 电缆以及光导纤维。) ·无线信道 (包括地波传播、短波电离层反射、 超短波或微波无线视距传输、卫星中继以及各 种散射信道等。) 2.广义信道:除了传输媒质外,还包括有关的 转换设备,如发送设备、接收设备、馈线与天 线、调制器、解调器等等。这种范围扩大了的 信道称为广义信道。分为: 调制信道 研究调制与解调的角度定义 2011/11/13 2
3.1、信道的定义与分类 1. 狭义信道:仅指传输媒质。分为: • 有线信道 (包括架空明线、对称电缆、同轴 电缆以及光导纤维。) • 无线信道 (包括地波传播、短波电离层反射、 超短波或微波无线视距传输、卫星中继以及各 种散射信道等。) 2. 广义信道:除了传输媒质外,还包括有关的 转换设备,如发送设备、接收设备、馈线与天 线、调制器、解调器等等。这种范围扩大了的 信道称为广义信道。分为: • 调制信道 研究调制与解调的角度定义 2011/11/13 2
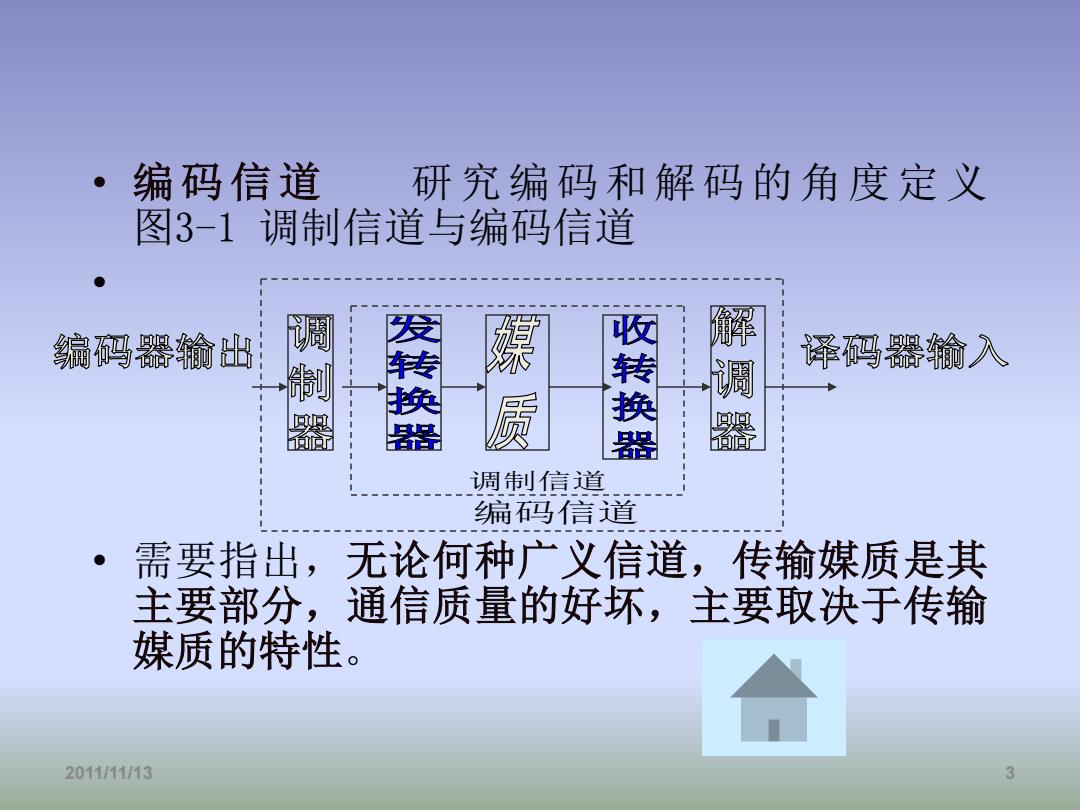
。 编码信道 研究编码和解码的角度定义 图3-1调制信道与编码信道 ● 编码器输出 调 收转换器 解 译码器输入 调 嗯 器 嗯 调制信道 编码信道 。1 需要指出,无论何种广义信道,传输媒质是其 主要部分,通信质量的好坏,主要取决于传输 媒质的特性。 2011/11/13
• 编码信道 研究编码和解码的角度定义 图3-1 调制信道与编码信道 • • 需要指出,无论何种广义信道,传输媒质是其 主要部分,通信质量的好坏,主要取决于传输 媒质的特性。 2011/11/13 3 编码信道 调制信道
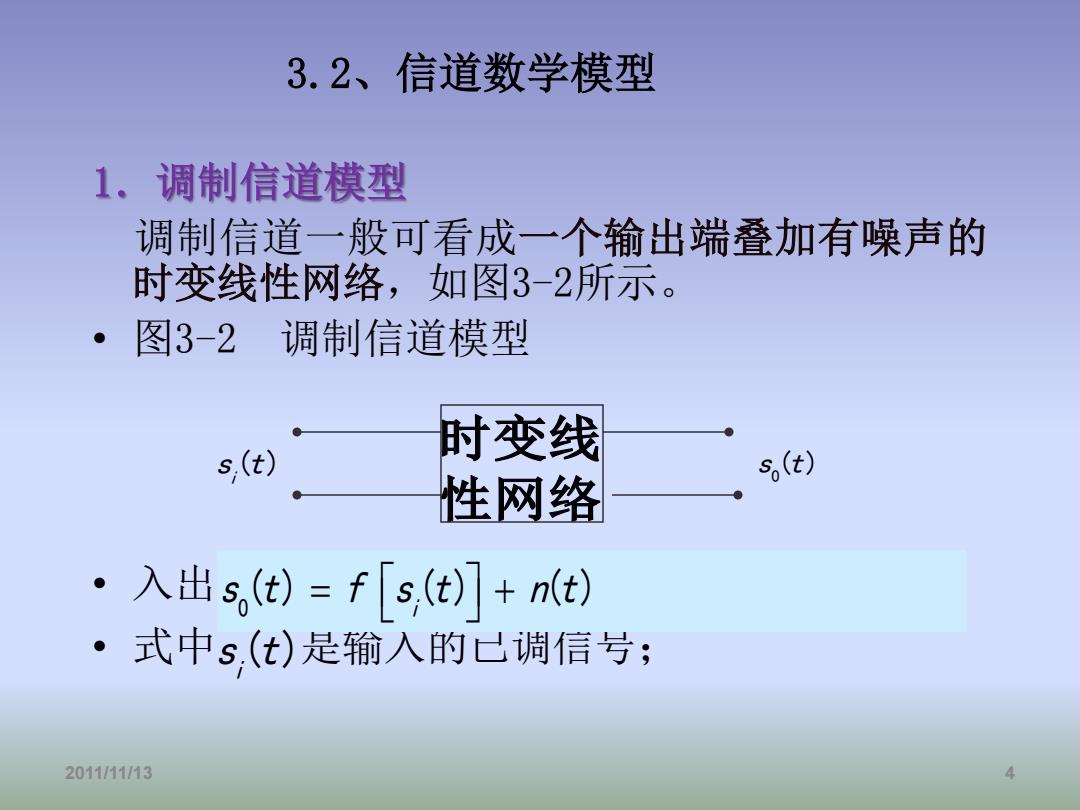
3.2、信道数学模型 1.调制信道模型 调制信道一般可看成一个输出端叠加有噪声的 时变线性网络,如图3-2所示。 ·图3-2调制信道模型 s,(t) 时变线 s,(t) 性网络 ·入出s,(t)=f[s,(t)]+nt) ·式中s.(t)是输入的已调信号; 2011/11/13
3.2、信道数学模型 1.调制信道模型 调制信道一般可看成一个输出端叠加有噪声的 时变线性网络,如图3-2所示。 • 图3-2 调制信道模型 • 入出关系: • 式中 是输入的已调信号; 2011/11/13 4 0 () () () i s t f s t nt = + ( ) i s t ( ) i s t 0 s t( )

·s,(t)是信道总的输出;5,(t)=c(t)s,(t)+n(t) n(t)是加性噪声(或称加性干扰), n(t0)与s,(t) 不发生依赖关系,或者说s,(t)独立于n(t) 。 ·作为数学上的一种简洁: ·c(t)依赖于网络特性,它对s,(t)来说是一种乘 性干扰。 ·讨论: ·(1)调制信道对信号的干扰有两种:乘性干 扰c(t)和加性干扰n).分析信道对信号的具体 影响,在于了解c(t)与n(t)的特性。 2011/11/13 5
• 是信道总的输出; • 是加性噪声(或称加性干扰), 与 不发生依赖关系,或者说 独立于 。 • 作为数学上的一种简洁: • 依赖于网络特性,它对 来说是一种乘 性干扰。 • 讨论: • (1)调制信道对信号的干扰有两种:乘性干 扰 和加性干扰 .分析信道对信号的具体 影响,在于了解 与 的特性。 2011/11/13 5 0 s t( ) n (t) n t( ) ( ) i s t ( ) i s t 0 ( ) ( )( ) ( ) i s t cts t nt = + ( ) i c t( ) s t c t( ) n(t) c t( ) n(t) n t( )

(2)分析乘性干扰c(t)的影响时,可把调制信 道分为两大类: 。 恒参信道,即c(t)随时间缓变或不变; ·随参信道,即c(t)随机快速变化。 。 通常,将架空明线、电缆、光导纡维、超短波 及微波视距传播、卫星审继等视为恒参信道。 西将短波患离层及射信道、各种散射信道、超 短波移动通信信道等视为随参信道。 2.编码信道模型 编码信道的特性可用信道转移概率(条件概 率)来描述。以二进制无记忆编码信道为例。 2011/11/13 6
• (2)分析乘性干扰 的影响时,可把调制信 道分为两大类: • 恒参信道,即 随时间缓变或不变; • 随参信道,即 随机快速变化。 • 通常,将架空明线、电缆、光导纤维、超短波 及微波视距传播、卫星中继等视为恒参信道。 而将短波电离层反射信道、各种散射信道、超 短波移动通信信道等视为随参信道。 2.编码信道模型 • 编码信道的特性可用信道转移概率(条件概 率)来描述。以二进制无记忆编码信道为例。 2011/11/13 6 c t( ) c t( ) c t( )
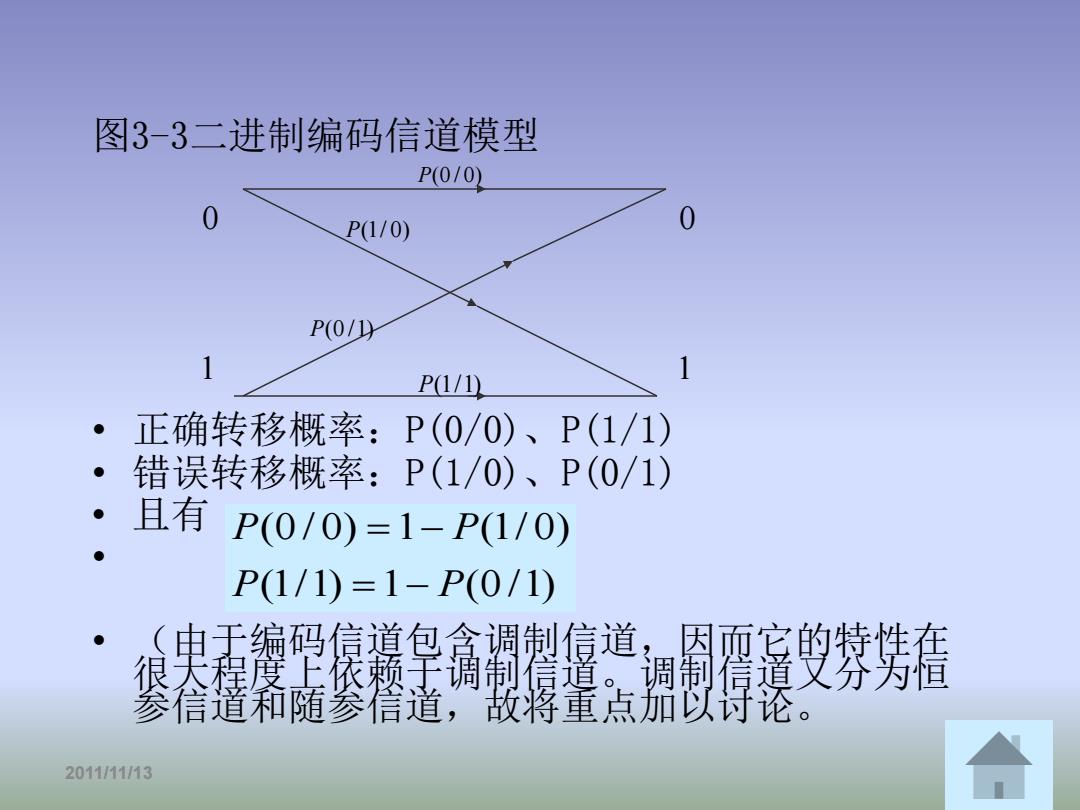
图3-3二进制编码信道模型 P(0/0) 0 P(1/0) 0 P(0/) P1/1 1 正确转移概率:P(0/0)、P(1/1) 。 错误转移概率:P(1/0)、P(0/1) 且有P(0/0)=1-P(1/0) ● P(1/1)=1-P(0/1) 尖囊卑高道度9棼美 参信道和随参信道,故将重点加以讨论。 2011/11/13
图3-3二进制编码信道模型 • 正确转移概率:P(0/0)、P(1/1) • 错误转移概率:P(1/0)、P(0/1) • 且有 • • (由于编码信道包含调制信道,因而它的特性在 很大程度上依赖于调制信道。调制信道又分为恒 参信道和随参信道,故将重点加以讨论。 2011/11/13 7 (1/1) 1 (0 /1) (0 / 0) 1 (1/ 0) P P P P = − = − 1 0 1 0 P(0 / 0) P(0 /1) P(1/ 0) P(1/1)

3.3、恒参信道的特性及其对信号的影响 。 恒参信道是指乘性干扰c(t)基本不随时间 变化的信道。因此,恒参信道可等效为 一个线性时不变网络。H(o)可用幅频特性 和相频特性共同来描述。 1.传输特性 H(@)=H(@e() ·幅频特性 H(@)~@ ·相频特性 0)心0 2011/11/13 8
3.3、恒参信道的特性及其对信号的影响 • 恒参信道是指乘性干扰 基本不随时间 变化的信道。因此,恒参信道可等效为 一个线性时不变网络。 可用幅频特性 和相频特性共同来描述。 1. 传输特性 • 幅频特性 • 相频特性 2011/11/13 8 c t( ) H(ω) ( ) () () j H He φ ω ω ω = H(ω) ~ ω φ(ω) ~ ω

·1.不失真条件 H(0)-Keior H(o)-o为一条水平线 ● p(ω)-o成线性关系 引入群迟延一频率特性,它定义为相频特性的 导数,即 x(ω)= do(o) dω 若(O)~0呈线性关系,则(@)~ω曲线是 一 条水平直线,如图3-4所示。这时,信号的不 同频率成分将有相同的时延,因而信号经过该 信道传输后将不发生失真。 2011/11/13 9
• 1.不失真条件 • • • 引入群迟延—频率特性,它定义为相频特性的 导数,即 • 若 呈线性关系,则 曲线是一 条水平直线,如图3-4所示。这时,信号的不 同频率成分将有相同的时延,因而信号经过该 信道传输后将不发生失真。 2011/11/13 9 ( ) ( ) ( ) j t H Ke H ω ω ω ω ϕω ω = − − 为一条水平线 成线性关系 ω φ ω τ ω d d ( ) ( ) = φ(ω) ~ ω τ (ω) ~ ω
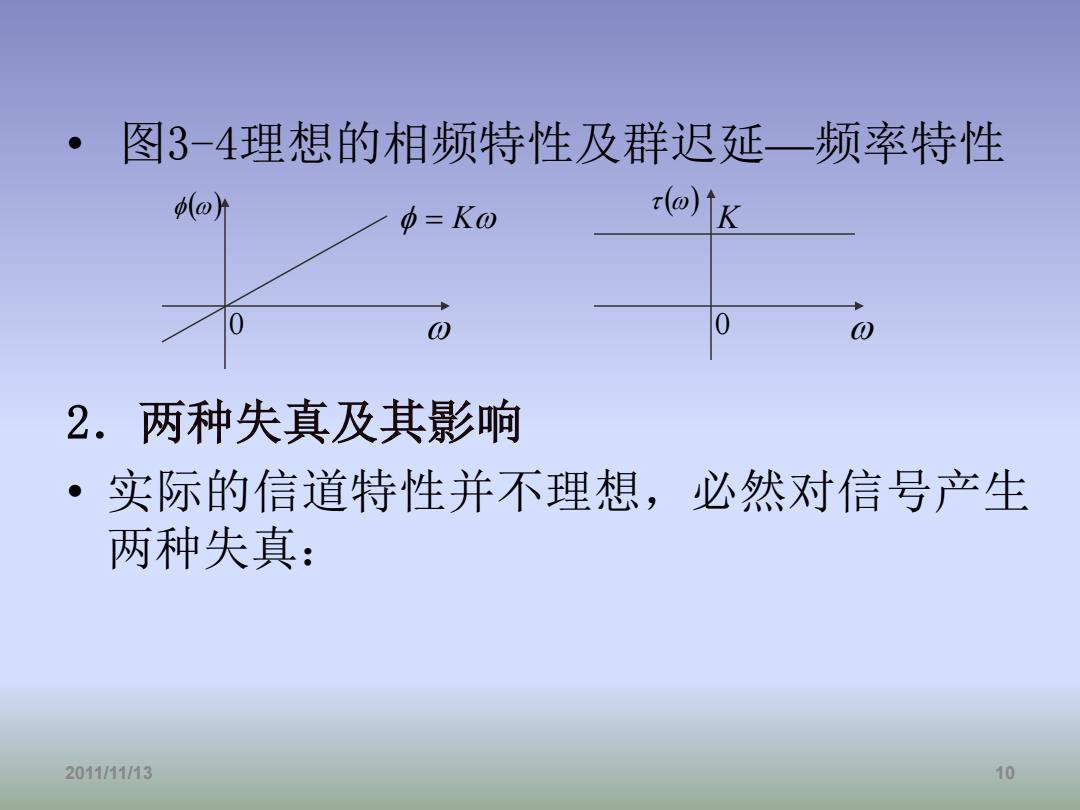
·图3-4理想的相频特性及群迟延一频率特性 =Ko r(@)iK 0 0 2.两种失真及其影响 实际的信道特性并不理想,必然对信号产生 两种失真: 2011/11/13 10
• 图3-4理想的相频特性及群迟延—频率特性 2.两种失真及其影响 • 实际的信道特性并不理想,必然对信号产生 两种失真: 2011/11/13 10 φ(ω) τ (ω) 0 0 K ω ω φ = Kω