6.3脉中编玛调制(PCM) 西安电子科技大学 通信工程学院SN 2)非均匀量化 思想:非均匀量化是一种在整个动态范围内量化间隔不相等的 量化。对于信号取值小的区间,其量化间隔也小;反之,量 化间隔就大。 X 压缩 均匀量化 扩张 非均匀量化 2012/10/29 第1页
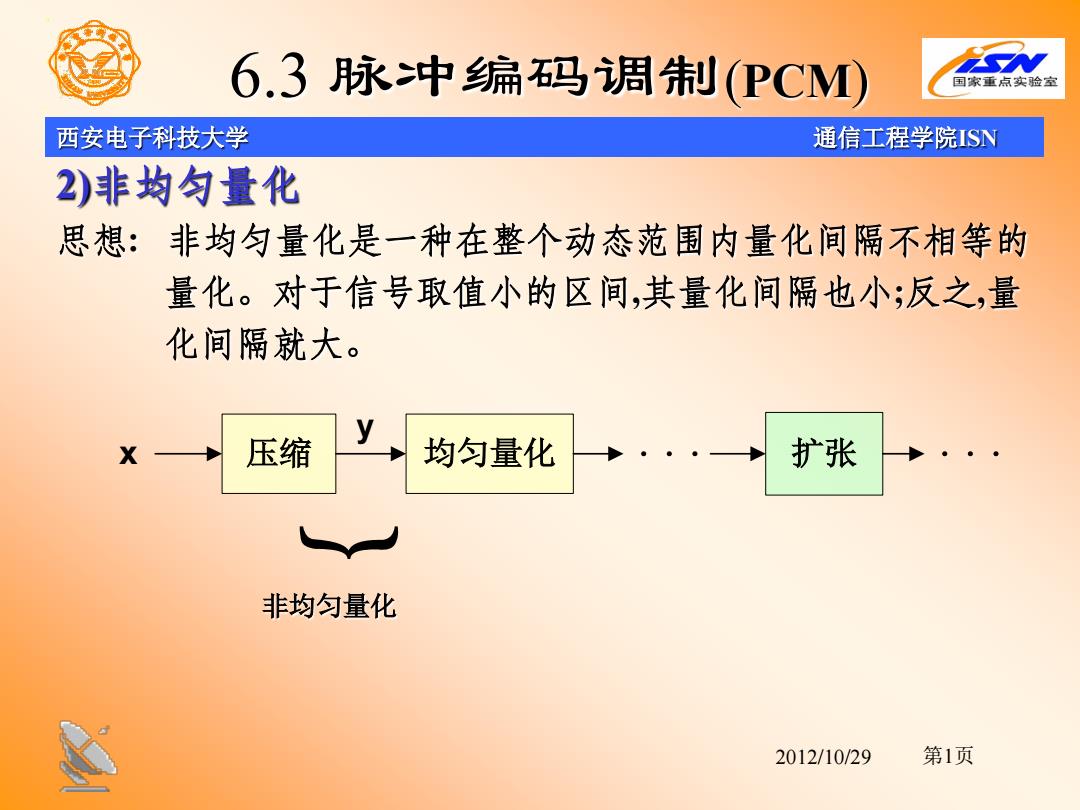
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 2)非均匀量化 思想: 非均匀量化是一种在整个动态范围内量化间隔不相等的 量化。对于信号取值小的区间,其量化间隔也小;反之,量 化间隔就大。 x 压缩 均匀量化 扩张 y 非均匀量化 ﹛ 第1页

6.3脉冲编码调制(PCM)) 国家重点实脸室 西安电子科技大学 通信工程学院ISN 非均匀量化与均匀量化相比,有两个突出的优点。 >当输入量化器的信号具有非均匀分布的概率密度时,非均 匀量化器的输出端可以得到较高的平均信号量化噪声功率 比; >非均匀量化时,量化噪声功率的均方根值基本上与信号抽样 值成正比。因此,量化噪声对大、小信号的影响大致相同, 即改善了小信号时的量化信噪比。 非均匀量化的实现方法是将抽样值通过压缩器压缩后再进 行均匀量化。 2012/10/29 第2页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 非均匀量化与均匀量化相比,有两个突出的优点。 当输入量化器的信号具有非均匀分布的概率密度时,非均 匀量化器的输出端可以得到较高的平均信号量化噪声功率 比 ; 非均匀量化时, 量化噪声功率的均方根值基本上与信号抽样 值成正比。因此,量化噪声对大、小信号的影响大致相同, 即改善了小信号时的量化信噪比。 非均匀量化的实现方法是将抽样值通过压缩器压缩后再进 行均匀量化。 第2页
6.3脉中编玛调制(PCM) 西安电子科技大学 通信工程学院SN 压缩器:压大补小,提高信号的S/Nq。 特性: 压扩后 X X t 压扩前 2012/10/29 第3页
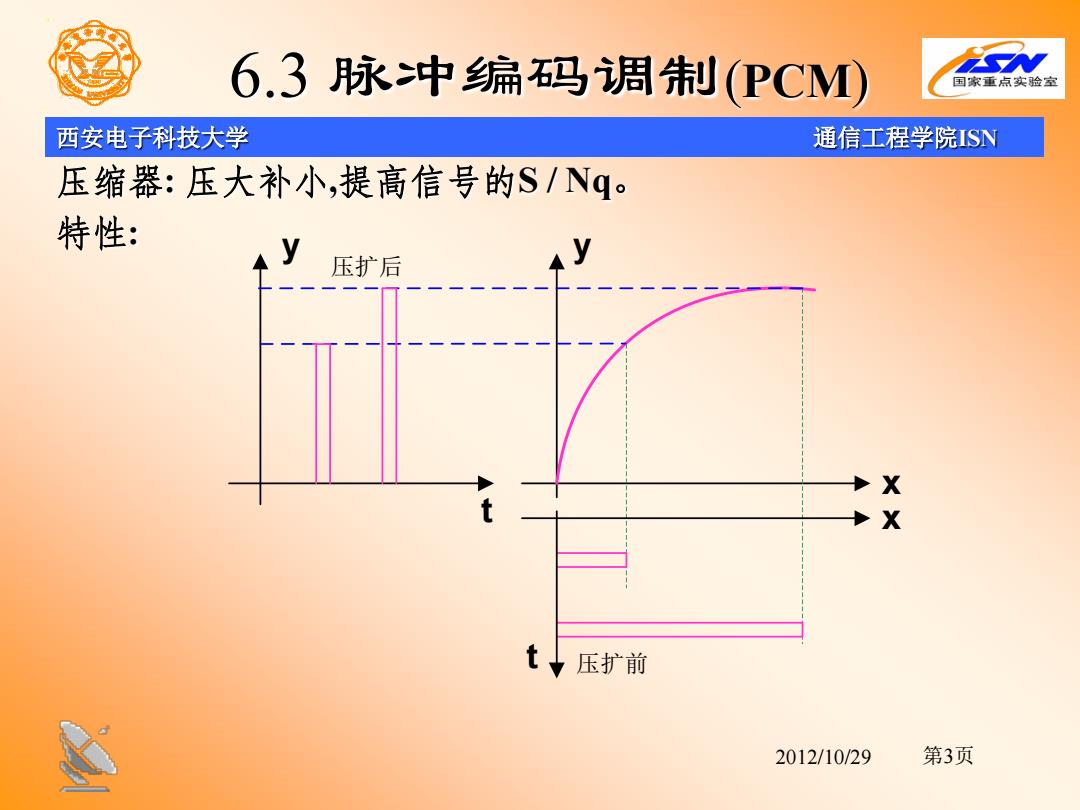
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 压缩器: 压大补小,提高信号的S / Nq。 特性: x y x y t t 压扩后 压扩前 第3页

6.3脉冲编码调制(PCM) 国家重点实脸室 西安电子科技大学 通信工程学院SN 广泛采用的两种对数压扩特性是μ律压扩和A律压扩。美国采 用律压扩,我国和欧洲各国均采用A律压扩,下面分别讨论这两 种压扩的原理。 4律压扩特性: ln(1+4x) y= ,0 ≤x≤1 ln(1+) 4=0 y=x X 2012/10/29 第4页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 广泛采用的两种对数压扩特性是 律压扩和A律压扩。美国采 用 律压扩,我国和欧洲各国均采用A律压扩,下面分别讨论这两 种压扩的原理。 律压扩特性: µ µ µ , 0 1 ln(1 ) ln(1 ) ≤ ≤ + + = x x y µ µ µ = 0 y x = x y 第4页

6.3脉中编玛调制(PCM 西安电子科技大学 通信工程学院SN x为归一化输入,y为归一化输出,归一化是指信号电压 与信号最大电压之比,所以归一化的最大值为1。八为压扩参 数,表示压扩程度。 山=0,无压缩; 4>100,标准中4=255。 A律压扩特性: Ax 0≤x≤ 1 1+In4 y= 1+In Ax ≤1 1+1nA A 2012/10/29 第5页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) x为归一化输入,y为归一化输出,归一化是指信号电压 与信号最大电压之比,所以归一化的最大值为1。 为压扩参 数,表示压扩程度。 =0 , 无压缩 ; >100 , 标准中 =255。 A律压扩特性: 1 0 1 ln 1 ln 1 1 1 ln Ax x A A y Ax x A A ≤ ≤ + = + ≤ ≤ + , , µ µ µ µ 第5页
6.3脉中编码调制(PCM0 国家重点实脸室 西安电子科技大学 通信工程学院ISN A为压扩参数,A=1时无压缩,A值越大压缩效果越明显。 少A dx 1+InA X 0111A =16 A=87.6 典型值 2012/10/29 第6页
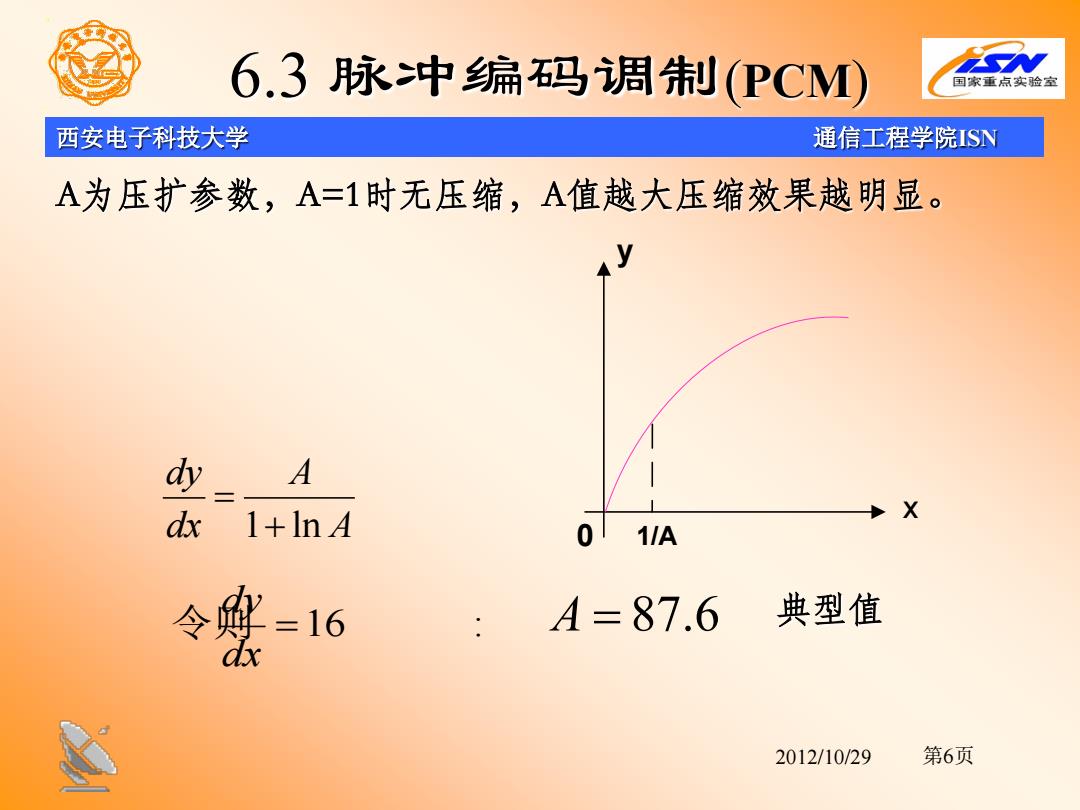
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) A为压扩参数,A=1时无压缩,A值越大压缩效果越明显。 典型值 x y 1 ln 0 1/A dy A dx A = + 16 : dy dx 令则 = A = 87.6 第6页

6.3脉中编玛调制(PCM) 西安电子科技大学 通信工程学院SN 下面举例来计算压缩对量化信噪比的改善量。 例:求“=00时,压缩对大、小信号的量化信噪比的改 善量,并与无压缩时(“=0)的情况进行对比。 解:因为压缩特性y=f(x)为对数曲线,当量化级划分较多 时,在每一量化级中压缩特性曲线均可看作直线 Ay d dy U 所以 .=y △x dx dx (1+ux)ln(1+) 有: 1 △x= △y 2012/10/29 第7页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 下面举例来计算压缩对量化信噪比的改善量。 例:求 时,压缩对大、小信号的量化信噪比的改 善量,并与无压缩时( )的情况进行对比。 解: 因为压缩特性 为对数曲线,当量化级划分较多 时,在每一量化级中压缩特性曲线均可看作直线 所以 有: µ = 100 µ = 0 y = f (x) ' y dx dy x y = = ∆ ∆ (1 µ )ln(1 µ) µ + + = dx x dy y y ∆x = ∆' 1 第7页

6.3脉中编码调制(PCM 国家重点实脸室 西安电子科技大学 通信工程学院ISN 因此,量化误差为 △x =1.y-△y.1+ux)ln(1+4 2y22 L 当u〉1时,△y/△x的比值大小反映了非均匀量化(有压 缩)对均匀量化(无压缩)的信噪比的改善程度。当用分贝表 示时,并用符号Q表示信噪比的改善量 那么 2012/10/29 第8页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 因此,量化误差为 当 〉1时, 的比值大小反映了非均匀量化(有压 缩)对均匀量化(无压缩)的信噪比的改善程度。当用分贝表 示时,并用符号Q表示信噪比的改善量 µ (1 µ )ln(1 µ) 2 2 1 2 ' + + ⋅ ∆ = ∆ = ⋅ ∆ y y x y x µ ∆y / ∆x 那么 [ ] = ∆ ∆ = dx dy x y Q dB 20lg 20lg 第8页

6.3脉中编玛调制(PCM) 西安电子科技大学 通信工程学院SN 对小信号(x→0)时 有 dy 100 dx r-0 (1+ux)ln(1+4) ln(1+) 4.62 该比值大于1,表示非均匀量化的量化间隔△x比均匀量化间隔 小。 这时,信噪比的改善量为 L。0Ea】 =26.7 2012/10/29 第9页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 对小信号( )时 有 该比值大于1,表示非均匀量化的量化间隔 比均匀量化间隔 小。 这时,信噪比的改善量为 x → 0 4.62 100 ln(1 ) | (1 )ln(1 ) 0 0 = + = + + = → → µ µ µ µ µ X X dx x dy ∆x [ ] 20lg = 26.7 = dx dy Q dB 第9页

6.3脉冲编码调制(PCM 国家重点实脸室 西安电子科技大学 通信工程学院ISN 对大信号(x=1)时,有 100 1+4x)ln(1+) (1+100)1n(1+100) 4.67 该比值小于1,表示非均匀量化的量化间隔△x比均匀量化间隔 △y大,故信噪比下降。以分贝表示为 =2we[)2046 =-13.3 即大信号信噪比下降13.3dB。 2012/10/29 第10页
西安电子科技大学 通信工程学院ISN 2012/10/29 6.3 脉冲编码调制(PCM) 对大信号( )时, 有 该比值小于1,表示非均匀量化的量化间隔 比均匀量化间隔 大,故信噪比下降。以分贝表示为 即大信号信噪比下降13.3 。 x = 1 4.67 1 (1 100)ln(1 100) 100 | (1 )ln(1 ) 1 1 = + + = + + = = = x x dx x dy µ µ µ ∆x ∆y [ ] 13.3 4.67 1 20lg 20lg = − = = dx dy Q dB dB 第10页