西安电子科技大学：《信号检测与估值》课程教学资源（课件讲稿，2019）第一章 高斯信道上的信号检测

信号检测与估值2019年秋季 西电通院郑贱平 第一章：高斯信道的信号检测 1.1问题描述 1.2 Bayesi检测 1.3二元实高斯信号检测 1.4充分统计量服从高斯分布时的PEP一般计算公式 1.5派生Bayes检测 1.6二元复高斯信号检测 1.7多元复高斯信号检测

信号检测与估值 2019年秋季 西电通院郑贱平 第 章一 ：高斯信道的信号检测 1.1 问题描述 1 2. Bayes检测 1.3 二元实高斯信号检测 1.4 充分统计量服从高斯分布时的PEP一般计算公式 1 5. 派生Bayes检测 1.6 二元复高斯信号检测 1.7 多元复高斯信号检测

1.1问题描述(problem formulation)) 。信号模型 r=x+n >x:输入信号，取自有限大小的信号星座（如PSK/QAM),i.e,x∈X >r:输出信号，r∈C >m:高斯噪声n~CW(0,No) 。问题描述： >1)根据y和噪声方差，按照一定的准则确定x为有限大小信号 星座中的哪一点 >2)采用该检测方法的性能评价 >Recall《通原》上的结果 e方法：贝叶斯(Bayes)检测 >通原上的最大似然(ML)检测是Bayest检测的一个特例 >《通原》上直接给出了计算方法和结果，这里我们解决为什么 这么做并将之进行推广的问题。 信号检测与估值2019年秋

1.1 问题描述(problem formulation) 信号模型 r=x+n  x: 输入信号，取自有限大小的信号星座（如PSK/QAM), i.e., x  r: 输出信号，  n: 高斯噪声 问题描述： r  n N   0, 0  问题描述：  1）根据y和噪声方差，按照一定的准则确定x为有限大小信号 星座中的哪一点  2）采用该检测方法的性能评价  Recall 《通原》上的结果 方法：贝叶斯（Bayes）检测  通原上的最大似然（ML）检测是Bayes检测的一个特例  《通原》上直接给出了计算方法和结果，这里我们解决为什么 这么做并将之进行推广的问题 信号检测与估值 2019年秋 2

1.2 Bayes检测 Bayes检测：平均代价最小的检测 。建模 。平均代价定义 。Bayes判决规则 。Bayes检测性能 Special cases 信号检测与估值2019年秋

1.2 Bayes检测 Bayes检测：平均代价最小的检测 建模 平均代价定义 Bayes判决规则 Bayes检测性能 Special cases 信号检测与估值 2019年秋 3

建模 。二元检测模型 Ho Ho成立 概率 信源 转移机构 观测空间 判决规则 H H成立 ·信源（信号空间） >信源的输出称为假设；BPSK=+1,-1); 。概率转移机构（噪声空间) >将信源的输出（假设）以一定的概率关系映射到整个观察空间 中；r=x+n ·观测空间 >接收端所有可能观测量的集合；r 。判决规则 >将观察空间进行合理划分，使每个观测量对应一个假设判断的方法； x=-1 if r<0,and x=+1,otherwise 信号检测与估值2019年秋

建模 二元检测模型 信源 概率 转移机构 观测空间 判决规则 H0 H1 H0成立 H1成立 信源（信号空间）  信源的输出称为假设;BPSK={+1，-1｝； 1  信源的输出称为假设;BPSK {+1， 1｝； 概率转移机构（噪声空间）  将信源的输出(假设)以一定的概率关系映射到整个观察空间 中;r=x+n 观测空间  接收端所有可能观测量的集合; r 判决规则  将观察空间进行合理划分,使每个观测量对应一个假设判断的方法; 信号检测与估值 2019年秋 4 x=-1 if r<0, and x=+1, otherwise

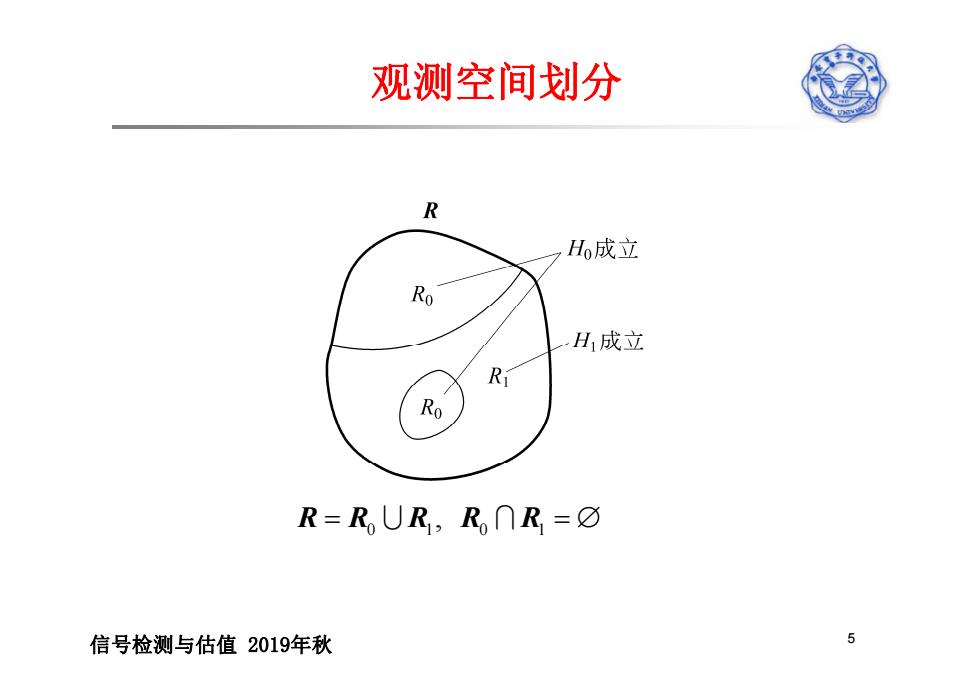
观测空间划分 R H成立 四 H1成立 R Ro R=RUR,R∩R=☑ 信号检测与估值2019年秋 5

观测空间划分 0 10 1 R  R RR R   ,   信号检测与估值 2019年秋 5

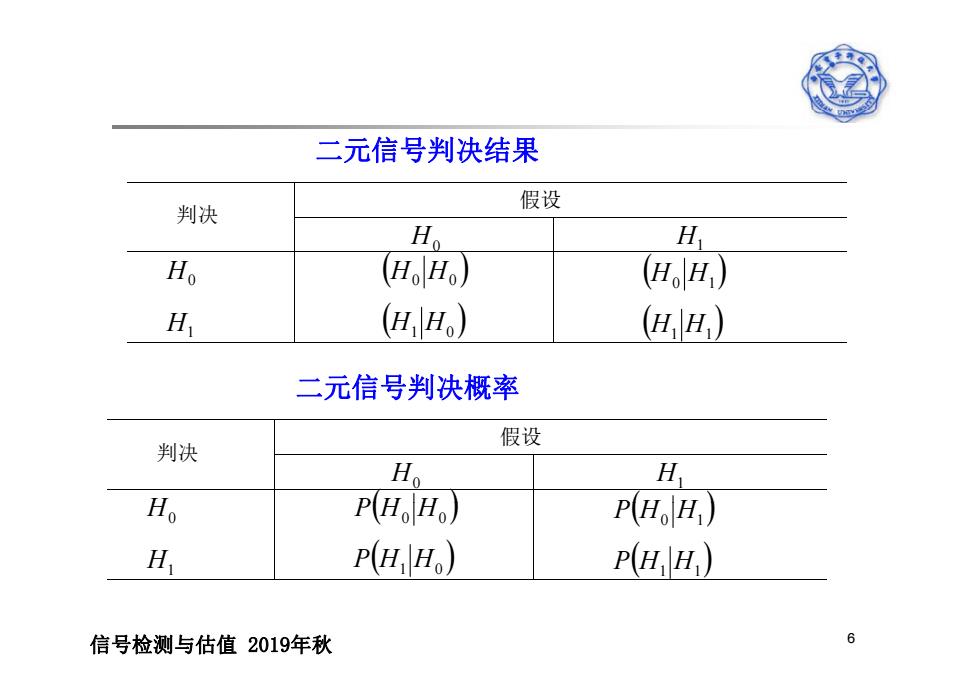
二元信号判决结果 判决 假设 Ho H Ho (HoHo) (HH) H. (HHo） HH) 二元信号判决概率 假设 判决 Ho H Ho P(HoHo) P(HoH) H P(HH) P(HH) 信号检测与估值2019年秋 6

二元信号判决结果 判决 假设 H0 H1 H H0 H0  H H  0 1   H1 H0   H1 H1 H0 H1 二元信号判决概率 判决 假设 H0 H1 H PH0 H0  PH H  P H0 H1   P H1 H0   P H1 H1 H0 H1 信号检测与估值 2019年秋 6

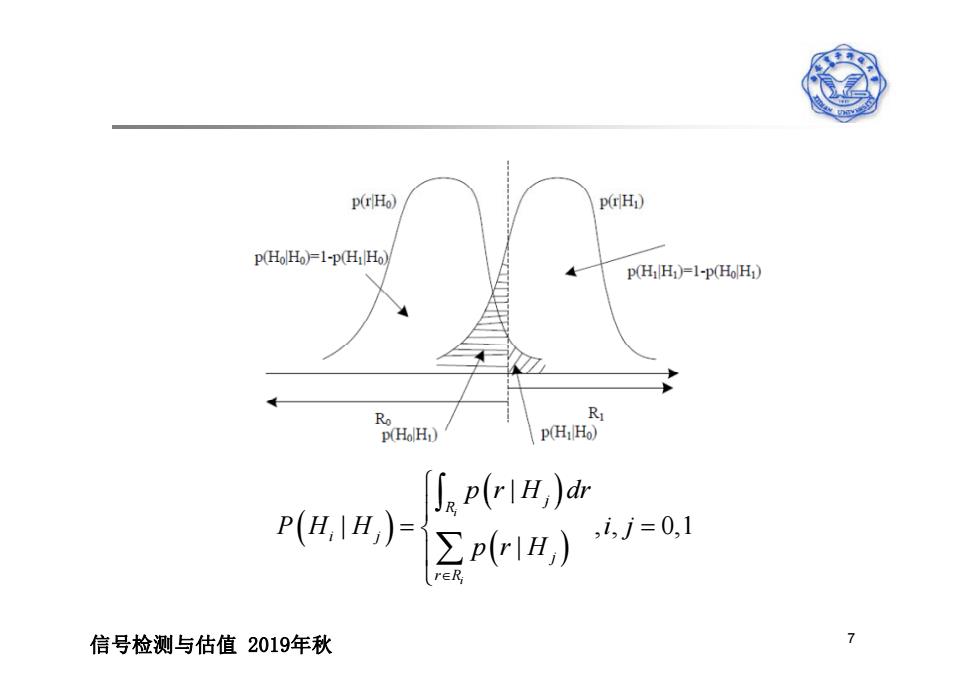
p(rHo) p(rH) p(Ho]Ho)=1-p(HiHo) P(H:H)=1-p(HoH) R p(HoH:) p(HHo) ep川H,)d (H) ∑p(rIH,) i,j=0,1 信号检测与估值2019年秋

 | j R  p r H dr        | | , , 0,1 | i i j R i j j r R p PH H ij prH        信号检测与估值 2019年秋 7  i

平均代价 。不同的事件赋予不同的代价(HH)→c >一般的，c102c0,co1>C1 ●平均代价表示式 C=P(Ho)C(Ho)+P(H)C(H) ()(n) C(Ho)=CooP(Ho Ho)+CoP (HHo) C(H)=coP(Ho H)+cP(HH) 信号检测与估值2019年秋

平均代价 不同的事件赋予不同的代价（Hi|Hj）cij  一般的，c10>c00, c01>c11, 平均代价表示式 C PH CH PH CH    0 0 11           1 1 0 0 | ij j i j j i cP H P H H                 CH cPH H cPH H 0 00 0 0 10 1 0 C   CH cPH H cPH H 1 01 0 1 11 1 1        信号检测与估值 2019年秋 8

Problem Formulation 。目标函数：C ·已知条件：P,cP(r|H,),RUR=RR∩R=② ·问题：如何对观测空间R进行划分（即确定R,、R)使得目标函数 C最小（贝叶斯准则)，即 minC R1.Ro st.P(H).P(rH)CRUR=R,RR= Q需要将C表示为PH),cR,R1,P(rH)的函数 。因此首先将RUR=R,R∩R=O表示为 P(RIH)=P(rIH)dr=1,j=0.1 P(HH)=5P(rIH)dr=SP(rIH)dr-fP(rlH)dr=1-P(HH) 信号检测与估值2019年秋

Problem Formulation 目标函数： C 已知条件：P( H ) P r H R R RR R  |     j ), cij, 问题：如何对观测空间 R进行划分（即确定 R 0 、 R 1）使得目标函数 C最小（贝叶斯准则），即   01 01 | , , P r H R R RR R j      1 0 , min R R  C   需要将 C表示为P( H ) c R R 的函数     01 01 . . , | , , , j j ij st P H P r H c R R R R R         需要将 C表示为P( H Pr H  |  j ), cij ,R 0,R 1, 的函数 因此首先将 表示为 01 01 R R RR R    ,   Pr H  | j                | | 1, 0,1 | | | | 1| j j R P R H P r H dr j PH H P H d P H d P H d PH H      01 01 信号检测与估值 2019年秋 9           0 1 0 1 | | | | 1| j jjj j R RR PH H P       r H dr P r H dr P r H dr PH H

Solution C=cooP(Ho)P(HoHo)+cioP(Ho)P(HHo) +coP(H)P(HH)+cuP(H)P(HH) =coP(H)P(rH)dr+cP(H)P(rH)dr (P()dr+()P()dr =coP(H)P(rHo)dr+cP(H)-cP(H)P(rH)dr +cP(H)P()dr+cp(H)-cP(H)S P(H)dr ) =cP(H)+GP(H,)+∫R P(H)(co-cu)P(rH)-P(Ho)(Co-coo)P(rH) const ●MinC→将所有r)O的r ·反证法证明 >存在某个满足fr存在某个满足fr)>0的r属于R,将其放入R,后的代价C'=C-)△KC 信号检测与估值2019年秋 10

Solution                 C cPH PH H cPH PH H 00 0 0 0 10 0 1 0 cPH PH H cPH PH H                            0 1 01 1 0 1 11 1 1 1 00 0 0 10 0 0 | R R cPH PH H cPH PH H c P H P r H dr c P H P r H dr c P H P r H dr c P H P r H dr                                 0 1 0 0 01 1 1 11 1 1 00 0 0 10 0 10 0 0 R R R R c P H P r H dr c P H P r H dr c P H P r H dr c P H c P H P r H dr PH P H d PH          PH P H d            f(r) 0 01 1 1 11 1 R  c PH P r H dr c  P H                    0 0 11 1 1 10 0 11 1 1 01 11 1 0 10 00 0 R R c PH P r H dr c P H c P H P H c c P r H P H c c P r H dr              f(r) Min C将所有f(ri)0的ri 0 0 ( ) ( ) i i R r R const f r dr const f r r        Min C将所有f(ri) 0的ri均放入判决区R0，且R0不包括任何f(ri) 0的ri 反证法证明  存在某个满足f(rk)0 的rk属于R0，将其放入R1后的代价C’=C- f(rk)Δr<C