西安电子科技大学：《信号检测与估值》课程教学资源（课件讲稿，2019）第四章 波形信号检测

信号检测与估值2019年秋 西电通院郑贱平 第四章波形信号检测 口二元信号波形检测模型 ▣匹配滤波器 口正交级数展开 口波形信号检测

信号检测与估值 2019年秋 西电通院郑贱平 第四章 波形信号检测 二元信号波形检测模型 匹配滤波器 正交级数展开 波形信号检测

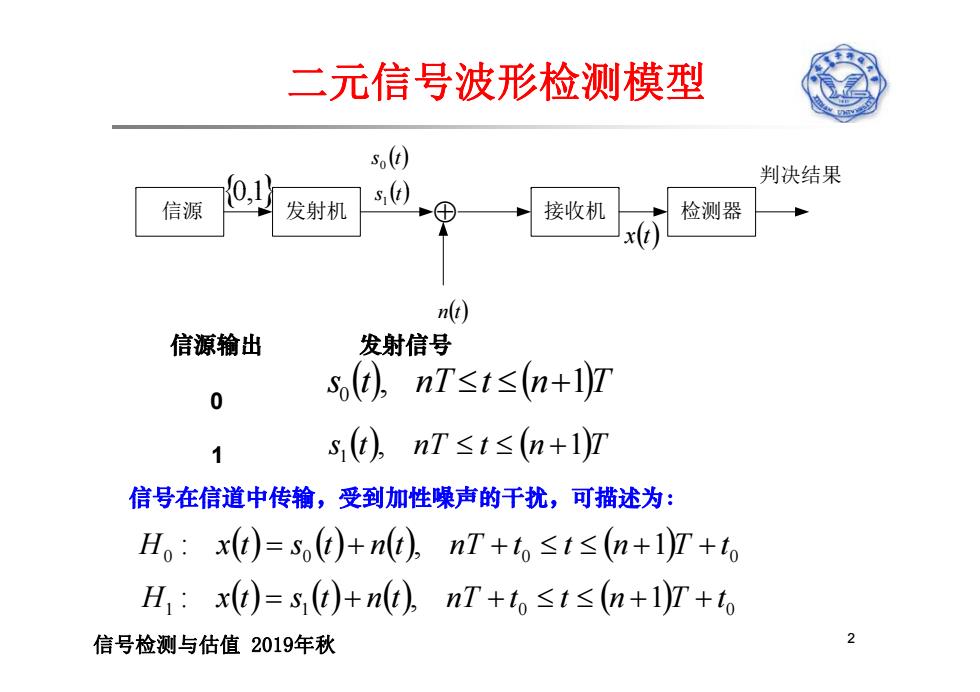
二元信号波形检测模型 ) 判决结果 0,1 信源 发射机 接收机 检测器 x(t n() 信源输出 发射信号 0 s,(),nT≤t≤n+1☑ 1 s,t),nT≤t≤(n+1)7 信号在信道中传输，受到加性噪声的干扰，可描述为： H。:xt)=st)+nt),nT+t≤t≤(n+lT+to H1:xt)=s(t)+nt),nT+t。≤t≤(n+1)T+to 信号检测与估值2019年秋 2

二元信号波形检测模型 判决结果 s  t  0  0 1   t  信源 发射机  接收机 检测器  0,1  s  t  1 x  t  n  t  信源输出 发射信号 0 s 0  t , nT  t   n  1  T 1 s1 t , nT  t   n  1 T 信号在信道中传输 信号在信道中传输，受到加性噪声的干扰 受到加性噪声的干扰，可描述为：         0 0 0 0 H : x t  s t  n t , nT  t  t  n  1 T  t         信号检测与估值 2019年秋 2         1 1 0 0 H : x t  s t  n t , n T  t  t  n  1 T  t

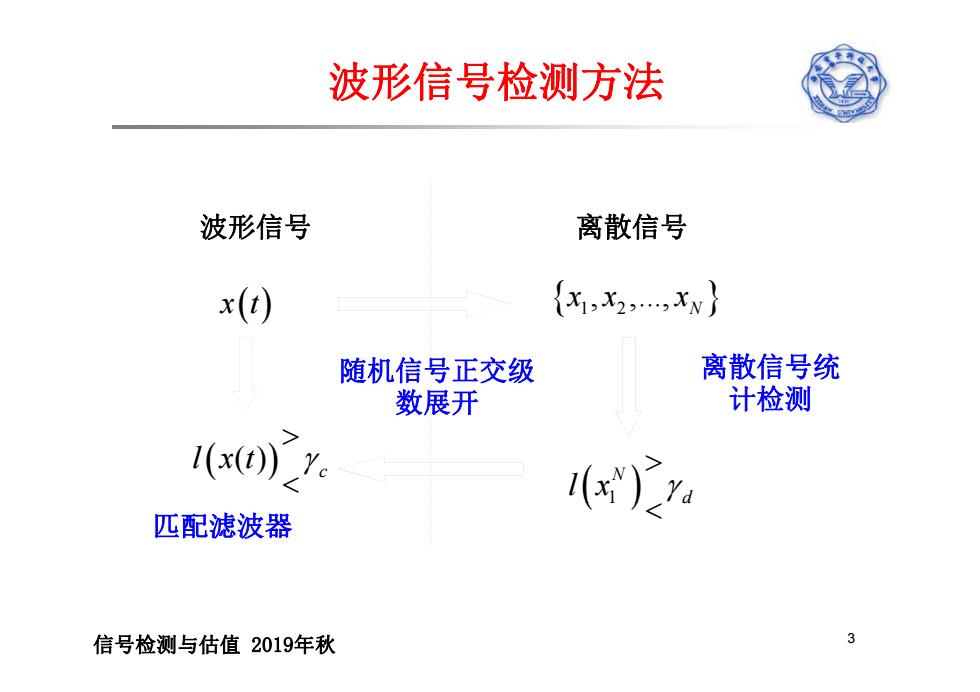
波形信号检测方法 波形信号 离散信号 x() {x1,x2,,xw} 随机信号正交级 离散信号统 数展开 计检测 1(x()Y (x) 匹配滤波器 信号检测与估值2019年秋

波形信号检测方法 波形信号 离散信号 x t    1 2 , ,..., N xx x 随机信号正交级 数展开 离散信号统 计检测  1  N d l x      ( ) c l xt     1  d  匹配滤波器 信号检测与估值 2019年秋 3

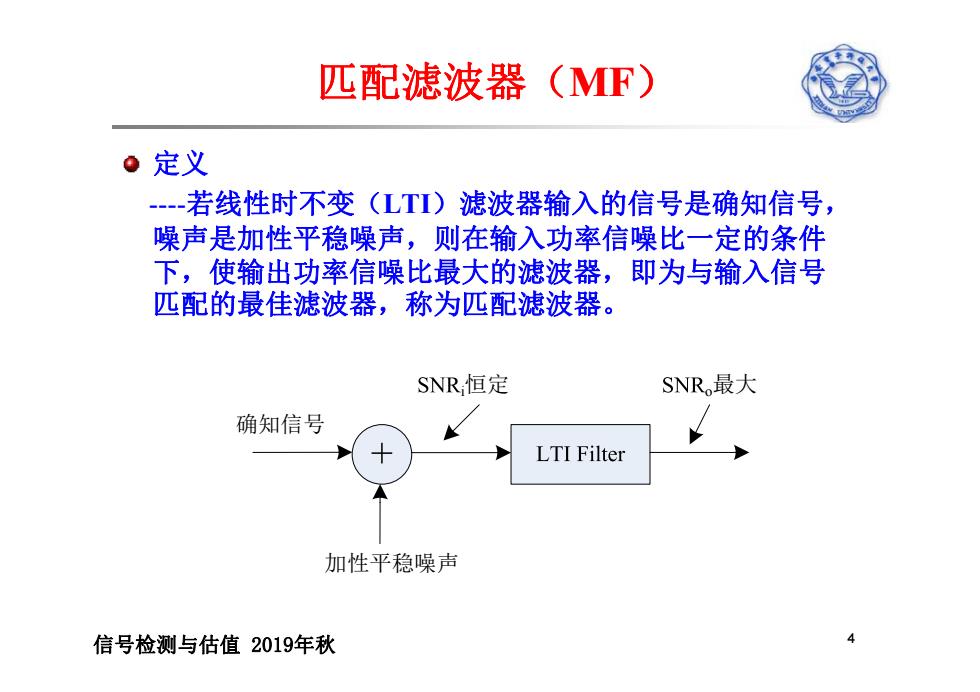
匹配滤波器 (MF) 。定义 -若线性时不变(LT)滤波器输入的信号是确知信号， 噪声是加性平稳噪声，则在输入功率信噪比一定的条件 下，使输出功率信噪比最大的滤波器，即为与输入信号 匹配的最佳滤波器，称为匹配滤波器。 SNR恒定 SNR,最大 确知信号 LTI Filter 加性平稳噪声 信号检测与估值2019年秋

匹配滤波器（MF） 定义 ----若线性时不变（LTI）滤波器输入的信号是确知信号， 噪声是加性平稳噪声，则在输入功率信噪比一定的条件 下，使输出功率信噪比最大的滤波器，即为与输入信号 匹配的最佳滤波器，称为匹配滤波器。 确知信号 i恒定 o最大 加性平稳噪声 信号检测与估值 2019年秋 4

系统模型 ●假设线性时不变滤波器的冲激相应为()，系统函数 为H(w),滤波器的输入信号为x()=s()+n(),滤波器 的输出信号为y()=s()+n()。 x0)=s0)+) yt)=3,)+n,) H(w) S(o)=[stedt E-∫s0h=2soho Q设计目标：输出功率信噪比最大。 信号检测与估值2019年秋

系统模型 假设线性时不变滤波器的冲激相应为h( )t ，系统函数 为H(w)，滤波器的输入信号为x(t)=s(t)+n(t)，滤波器 的输出信号为y(t)=so(t)+no 的输出信号为y( ) o( ) o( )t 。 xt  st nt yt s t n t xt  st nt  o  o y      o o S   s t e dt jt      Es s tdt S d       2 2 21 设计目标：输出功率信噪比最大。       s  2  信号检测与估值 2019年秋 5 设计目标：输出功率信噪比最大

设计思路 时域 h(t) s() s() S(w) S。(w) 频域 H(w) S(w)=FT{s())=s(t)e-mdr FS)SGr)e" 信号检测与估值2019年秋

设计思路 h(t) 时域 s t  s t 0   h(t) 域 S w  S w o   频域 H(w)    ( )   jwt S w FT s t s t e dt                ( ) 1 () ( ) jwt S w FT s t s t e dt s t IFT S w S w e dw         信号检测与估值 2019年秋 6 () ( )     2 

Formulation ●目标：输出信号功率信噪比定义为输出信号s()的峰值功 率与噪声n,()的平均功率之比。 def SNRo 5(t)的功率 n(t)的平均功率 ●已知条件： s()=s0)*h) S,(-S)H) Fs-()di<s(5.(o"do P.(@)=H(@)'P.(0) s(a)t(o)edo 信号检测与估值2019年秋

Formulation 目标：输出信号功率信噪比定义为输出信号so(t)的峰值功 率与噪声no(t)的平均功率之比。   def o s t SNR 的功率 已知条件：     o O o SNR n t  的功率 的平均功率 已知条件： s t st h(t) o   S  SH     ( ) o  o       o     12 j t o o st S e d         2 E s t dt             2 1 2 o o j t S H ed           P  H P  2 E s t dt S       信号检测与估值 2019年秋 7        2  Pn H Pn o 

Solution ·假设输出信号在t出现峰值，则输出信号的峰值功率为 k.(.F-slH@x"do 。输出噪声的平均功率为 [元(]=2R(oa z-JJH()r.(oHo 信号检测与估值2019年秋

Solution 假设输出信号在t0出现峰值，则输出信号的峰值功率为       2 2 0 1     s t S H e d j t   输出噪声的平均功率为       0 2     so t S H e d   输出噪声的平均功率为 1     2 2 1 o En t P d o n                1 2 2 H Pd  n       信号检测与估值 2019年秋 8

Solution def SNRo s,(t)的功率 n,(t)的平均功率 )s(ode 2元」n(o'pe(oa 信号检测与估值2019年秋

Solution   d f  的功率   def o O o s t SNR n t  的功率 的平均功率  0 2 1 2 j t H S ed            2 2 1 2 H Pd n          2 信号检测与估值 2019年秋 9

Cauchy-Schwarz不等式 2[r@Xr@X 等号成立的条件为 ()=aF(t) F()=S(@)e Q)=H(OP,(@) P.(@) Alternative form: lKa,b外≤adbl 信号检测与估值2019年秋 10

Cauchy-Schwarz Schwarz不等式 2 1 1 1 F  t Qtdt F tFtdt Q tQtdt        * * * 21 21 21   等号成立的条件为 Qt Ft    jt S e 0               Pn S e F*     Q  H Pn Alternative form： ab a b   信号检测与估值 2019年秋 10 ab a b , 