
国家重点实验室 第2章随机过程 2.1随机过程的基本概念和统计特性 2.2平稳随机过程 2.3高斯随机过程 2.4随机过程通过线性系统 2.5窄带随机过程 2.6正弦波加窄带高斯噪声 返回主且录
2.1随机过程的基本概念和统计特性 2.2平稳随机过程 2.3高斯随机过程 2.4随机过程通过线性系统 2.5窄带随机过程 2.6正弦波加窄带高斯噪声 第 2 章随机过程 返回主目录

国家重点实验室 本章要求: ◆随机过程的基本概念和数字特征(均值、方差、相关 函数); ◆平稳、高斯、窄带、正弦波加窄带高斯过程的统计特 性 ◆随机过程通过线性系统 ◆高斯白噪声和带限白噪声 西安皂子积科接大学
本章要求: 随机过程的基本概念和数字特征(均值、方差、相关 函数); 平稳、高斯、窄带、正弦波加窄带高斯过程的统计特 性 随机过程通过线性系统 高斯白噪声和带限白噪声 西安电子科技大学

国家重点实验室 2.1随机过程的基本概念和统计特性 2.1.1随机过程 自然界中事物的变化过程可以大致分成为两类。一类是其 变化过程具有确定的形式,或者说具有必然的变化规律,用 数学语言来说,其变化过程可以用一个或几个时间的确定函 数来描述,这类过程称为确定性过程。例如,电容器通过电 阻放电时,电容两端的电位差随时间的变化就是一个确定性 函数。而另一类过程没有确定的变化形式,也就是说,每次 对它的测量结果没有一个确定的变化规律,用数学语言来说, 这类事物变化的过程不可能用一个或几个时间的确定函数来 描述,这类过程称为随机过程。下面我们给出一个例子:
2.1 随机过程的基本概念和统计特性 2.1.1随机过程 自然界中事物的变化过程可以大致分成为两类。一类是其 变化过程具有确定的形式,或者说具有必然的变化规律,用 数学语言来说,其变化过程可以用一个或几个时间t的确定函 数来描述,这类过程称为确定性过程。例如,电容器通过电 阻放电时,电容两端的电位差随时间的变化就是一个确定性 函数。而另一类过程没有确定的变化形式,也就是说,每次 对它的测量结果没有一个确定的变化规律,用数学语言来说, 这类事物变化的过程不可能用一个或几个时间t的确定函数来 描述,这类过程称为随机过程。下面我们给出一个例子:

设有n台性能完全相同的接收机。我们在相同的工作环境 和测试条件下记录各台接收机的输出噪声波形(这也可以理解 为对一台接收机在一段时间内持续地进行n次观测)。测试结 果将表明,尽管设备和测试条件相同,记录的条曲线中找不 到两个完全相同的波形。这就是说,接收机输出的噪声电压随 时间的变化是不可预知的,因而它是一个随机过程。 由此我们给随机过程下一个更为严格的定义:设S(k=1, 2,)是随机试验。每一次试验都有一条时间波形(称为样本 函数或实现),记作x①,所有可能出现的结果的总体{x(①), x2(),…,X(),…}就构成一随机过程,记作ξ)。简言之,无 穷多个样本函数的总体叫做随机过程,如图2-1所示
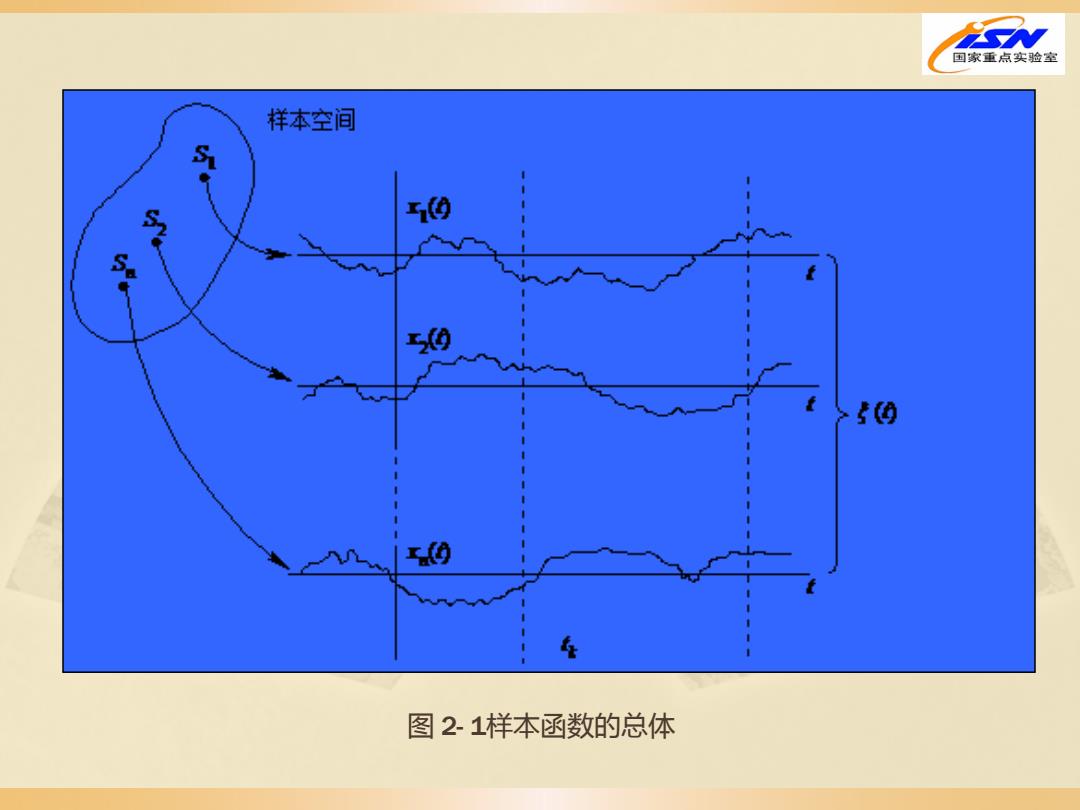
设有n台性能完全相同的接收机。我们在相同的工作环境 和测试条件下记录各台接收机的输出噪声波形(这也可以理解 为对一台接收机在一段时间内持续地进行n次观测)。测试结 果将表明,尽管设备和测试条件相同,记录的n条曲线中找不 到两个完全相同的波形。这就是说,接收机输出的噪声电压随 时间的变化是不可预知的,因而它是一个随机过程。 由此我们给随机过程下一个更为严格的定义:设Sk(k=1, 2, …)是随机试验。 每一次试验都有一条时间波形(称为样本 函数或实现),记作xi (t),所有可能出现的结果的总体{x1(t), x2(t), …, xn(t), …}就构成一随机过程,记作ξ(t)。简言之, 无 穷多个样本函数的总体叫做随机过程,如图 2 - 1 所示
S 国家重点实验室 样本空间 G 图21样本函数的总体
图 2- 1样本函数的总体

国家重点实验室 显然,上例中接收机的输出噪声波形也可用图2·1表示。 我们把对接收机输出噪声波形的观测可看作是进行一次随机 试验,每次试验之后,)取图2-1所示的样本空间中的某一 样本函数,至于是空间中哪一个样本,在进行观测前是无法 预知的,这正是随机过程随机性的具体表现。其基本特征体 现在两个方面:其一,它是一个时间函数;其二,在固定的 某一观察时刻t,全体样本在t时刻的取值ξt)是一个不含变 化的随机变量。因此,我们又可以把随机过程看成依赖时间 参数的一族随机变量。可见,随机过程具有随机变量和时间 函数的特点。下面将会看到,在研究随机过程时正是利用了 这两个特点
显然,上例中接收机的输出噪声波形也可用图 2 - 1 表示。 我们把对接收机输出噪声波形的观测可看作是进行一次随机 试验,每次试验之后,ξ(t)取图 2 - 1 所示的样本空间中的某一 样本函数,至于是空间中哪一个样本,在进行观测前是无法 预知的,这正是随机过程随机性的具体表现。其基本特征体 现在两个方面:其一,它是一个时间函数;其二,在固定的 某一观察时刻t1,全体样本在t1时刻的取值ξ(t1)是一个不含t变 化的随机变量。因此,我们又可以把随机过程看成依赖时间 参数的一族随机变量。可见,随机过程具有随机变量和时间 函数的特点。下面将会看到,在研究随机过程时正是利用了 这两个特点

国家重点实验室 2.1.2随机过程的统计特性 随机过程的两重性使我们可以用与描述随机变量相似的 方法,来描述它的统计特性。 设ξ()表示一个随机过程,在任意给定的时刻,∈T,其 取值()是一个一维随机变量。而随机变量的统计特性可以 用分布函数或概率密度函数来描述。我们把随机变量()小 于或等于某一数值x的概率P[t)SX1],简记为F1(&1,t1), 即F1(x,t=P[t)x1] (2.1-1) 式(2.1-1)称为随机过程()的一维分布函数
2.1.2随机过程的统计特性 随机过程的两重性使我们可以用与描述随机变量相似的 方法, 来描述它的统计特性。 设ξ(t)表示一个随机过程,在任意给定的时刻t1∈T, 其 取值ξ(t1)是一个一维随机变量。而随机变量的统计特性可以 用分布函数或概率密度函数来描述。我们把随机变量ξ(t1)小 于或等于某一数值x1的概率P[ξ(t1)≤x1],简记为F1(x1, t1), 即F1(x1,t1)=P[ξ(t1)≤x1] (2.1 - 1) 式(2.1 - 1)称为随机过程ξ(t)的一维分布函数

如果F(X,t)对x的偏导数存在,即有 国家重点实验室 aF(x1,4 8x1 2=f(x,4) 则称f(飞,t)为(①的一维概率密度函数。显然,随机过程的 维分布函数或一维概率密度函数仅仅描述了随机过程在各个 孤立时刻的统计特性,而没有说明随机过程在不同时刻取值之 间的内在联系,为此需要进一步引入二维分布函数。 任给两个时刻t,2∈T,则随机变量t)和(t2)构成一个二 元随机变量{(t),(t)},称 F2(K1x2;t1,t2)=P{t1)Xx1,t2)X2】 (2.1-3) 为随机过程ξ()的二维分布函数。如果存在
1 11 1 11 1 ( ,) ( ,) Fxt f xt x ∂ = ∂ 则称f1(x1, t1)为ξ(t)的一维概率密度函数。显然,随机过程的 一维分布函数或一维概率密度函数仅仅描述了随机过程在各个 孤立时刻的统计特性,而没有说明随机过程在不同时刻取值之 间的内在联系,为此需要进一步引入二维分布函数。 任给两个时刻t1, t2∈T,则随机变量ξ(t1)和ξ(t2)构成一个二 元随机变量{ξ(t1), ξ(t2)},称 F2(x1,x2; t1,t2)=P{ξ(t1)≤x1, ξ(t2)≤x2} (2.1 - 3) 为随机过程ξ(t)的二维分布函数。 如果存在 如果F1(x1, t1)对x1的偏导数存在,即有

国家重点实验室 a2F(x1,x2,42) Ox1·ox2 =f5(xx4) 则称f(x,X2;t1,2)为t)的二维概率密度函数。 同理,任给t1,t2,,t∈T,则()的n维分布函数被定义为 Fn(&1,X2,,Xnt1,2,,tn)=P{5(t1)X1,5(t2)X2,…,ξtn)Xn} a2F(x3h)=f(x,x2,x,1) ax1·Ox2.0xm
2 2 1 2 1, 2 2 1 212 1 2 (, ; ) ( , ;, ) F x x tt f xxtt x x ∂ = ∂ ⋅∂ 则称f2(x1,x2; t1,t2)为ξ(t)的二维概率密度函数。 同理,任给t1, t2, …, tn ∈T, 则ξ(t)的n维分布函数被定义为 Fn(x1,x2,…,xn;t1,t2,…,tn)=P{ξ(t1)≤x1,ξ(t2)≤x2,…, ξ(tn)≤xn} 2 1 2 1, 2 1 2 12 1 2 ( , ...; ..., ) ( , ..., ; , ..., ) ... ∂ = ∂ ⋅∂ ∂ n n n nn n F x x tt t f xx xtt t xx x

国家重点实验室 则称fn(X1,X2,,Xn,t1,t2,,n)为(t)的n维概率密度函数。显 然,越大,对随机过程统计特性的描述就越充分,但问题 的复杂性也随之增加。在一般实际问题中,掌握二维分布函 数就己经足够了
则称fn(x1,x2,…,xn; t1,t2,…,tn)为ξ(t)的n维概率密度函数。显 然,n越大,对随机过程统计特性的描述就越充分,但问题 的复杂性也随之增加。在一般实际问题中,掌握二维分布函 数就已经足够了