
State Key Laboratory of Integrated Services Networks 国家重点实验室 卷积码
State Key Laboratory of Integrated Services Networks 卷积码

N State Key Laboratory of Integrated Services Networks 国家重点实验室 卷积码基本概念 Convolutional Code
State Key Laboratory of Integrated Services Networks 卷积码基本概念 Convolutional Code

N 国家重点实验室 卷积码的提出 Encoding: 1955,Elias o Decoding: Threshold Decoding-Massey(1963) List Decoding Wozencraft(1961) Viterbi Decoding —Viterbi(1967)
卷积码的提出 Encoding:1955,Elias Decoding: Threshold Decoding —— Massey(1963) List Decoding —— Wozencraft(1961) Viterbi Decoding —— Viterbi (1967)

国家重点实验室 几个基本概念 编码存储:m, 信息组在编码器中需存储的单位 时间 编码约束度:N=叶1,编码过程中互相约束的码 段个数 编码约束长度:N4=(叶1)no,编码过程中互相约束 的码元个数 。译码约束度 。译码约束长度 。码率:R=k/no
几个基本概念 编码存储:m,信息组在编码器中需存储的单位 时间 编码约束度:N=m+1,编码过程中互相约束的码 段个数 编码约束长度:NA=(m+1)n0 ,编码过程中互相约束 的码元个数 译码约束度 译码约束长度 码率:R=k0 /n0
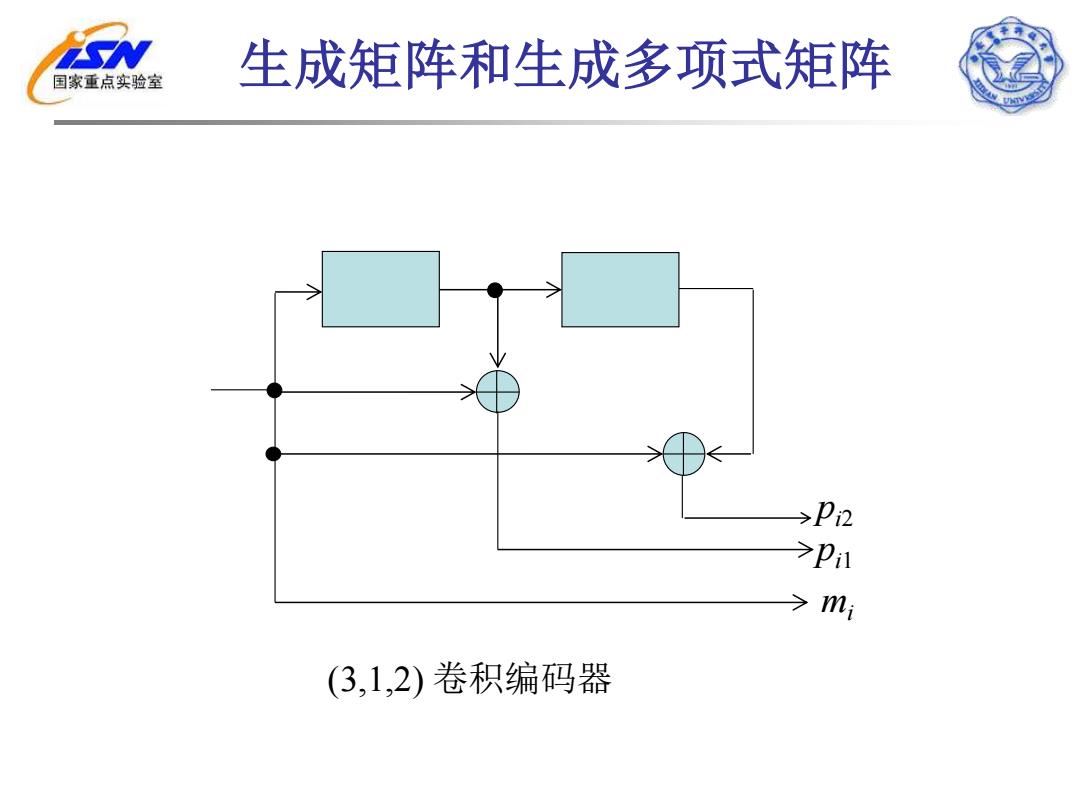
国家重点实验室 生成矩阵和生成多项式矩阵 >p2 >mi (3,1,2)卷积编码器
生成矩阵和生成多项式矩阵 mi pi2 pi1 (3,1,2) 卷积编码器

国家重点实验室 生成矩阵G 111 010 001 000 000 000 111 010 001 000 000 000 111 010 001 基本生成矩阵80 8=(111010 001000 000…)
生成矩阵G = 000 000 111 010 001 000 111 010 001 000 111 010 001 000 000 G 基本生成矩阵 = (111 010 001 000 000 ) g g

国家重点实验室 基本生成矩阵 g%=(111010001000000…) 子生成元 g=(100)g12=010)g3=(101) 生成多项式矩阵 G(D)=(1+D1+D2)
生成多项式矩阵 ( ) ( ) 2 G D = 1 1 + D 1 + D 基本生成矩阵 = (111 010 001 000 000 ) g 子生成元 (100) 1,1 g = (110) 1,2 g = (101) 1,3 g =
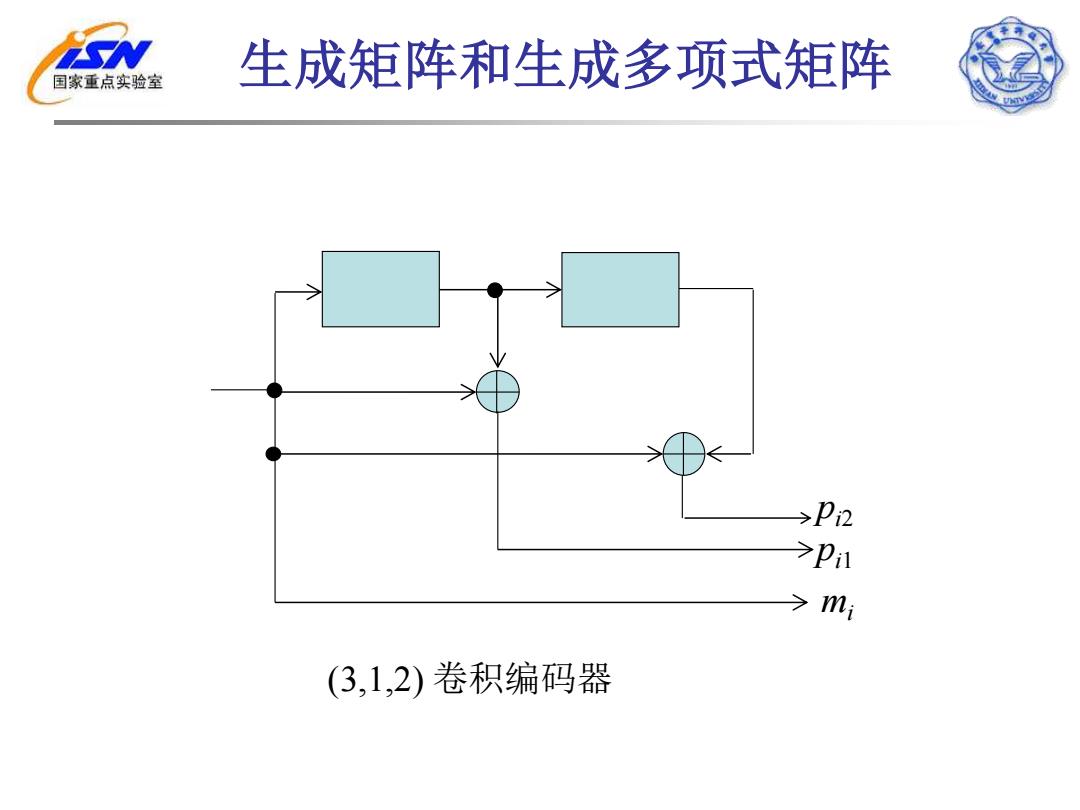
国家重点实验室 生成矩阵和生成多项式矩阵 >P2 >p1 >mi (3,1,2)卷积编码器
生成矩阵和生成多项式矩阵 mi pi2 pi1 (3,1,2) 卷积编码器
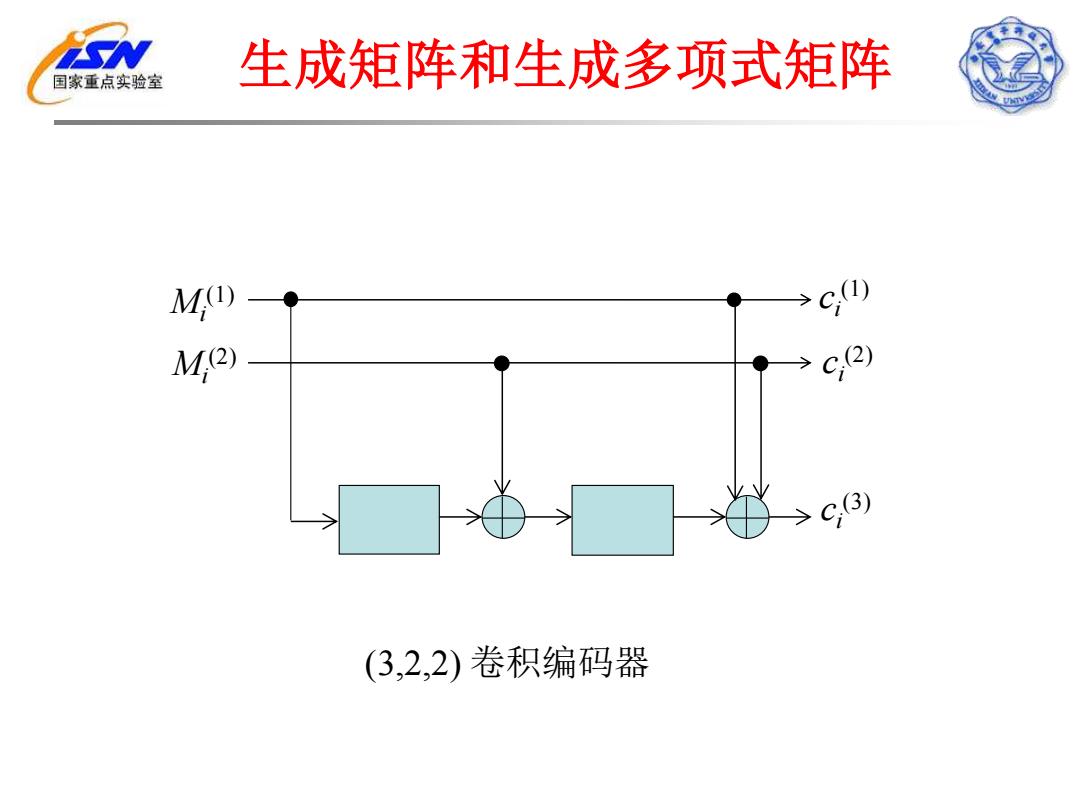
国家重点实验室 生成矩阵和生成多项式矩阵 M四 M2) >C2) C3) (3,2,2)卷积编码器
生成矩阵和生成多项式矩阵 Mi (1) Mi (2) ci (2) ci (1) ci (3) (3,2,2) 卷积编码器
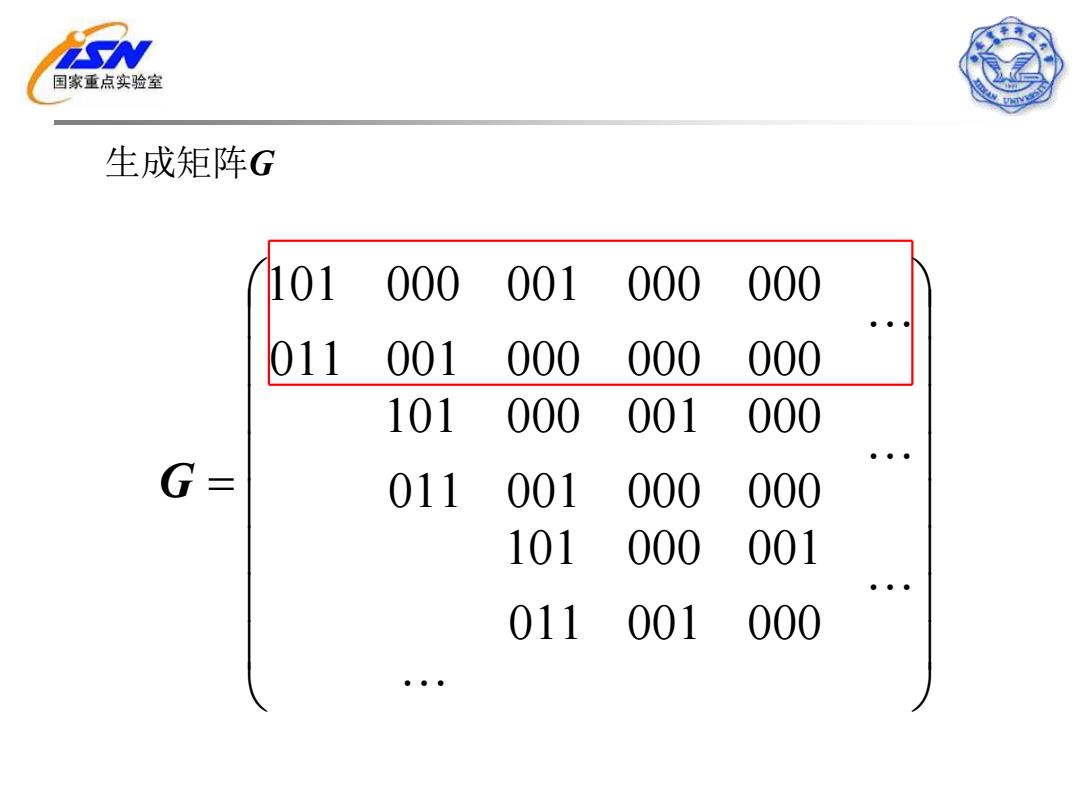
N 国家重点实验室 生成矩阵G 101 000 001 000 000 011 001 000 000 000 101 000 001 000 G= 011 001 000 000 101 000 001 011 001 000
生成矩阵G = 000 001 001 000 011 101 000 000 000 001 001 000 011 101 000 000 000 000 000 001 001 000 011 101 G