
第八章二端口网络 8.1二端口网络的方程与参数 一、Z参数方程和Y参数方程 二、A参数方程◆ 西安电子科技大学电路与系统多媒体室制作 三、H参数方程◆ 四、各种参数之间的关系 8.2二端口网络的网络函数 一、用Z参数表示网络函数 二、用A参数表示网络函数 三、特性阻抗 动 8.3二端口网络的等效 一、二端口网络的Z参数等效电路 二、二端口网络的Y参数等效电路 8.4二端口网络的级联 点击日录,进入相关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 点击目录 ,进入相关章节 8.1 二端口网络的方程与参数 一、Z参数方程和Y参数方程 二、A参数方程 三、H参数方程 四、各种参数之间的关系 8.2 二端口网络的网络函数 一、用Z参数表示网络函数 二、用A参数表示网络函数 三、特性阻抗 8.3 二端口网络的等效 一、二端口网络的Z参数等效电路 二、二端口网络的Y参数等效电路 8.4 二端口网络的级联 第 8-1 页 前一页 下一页 退出本章
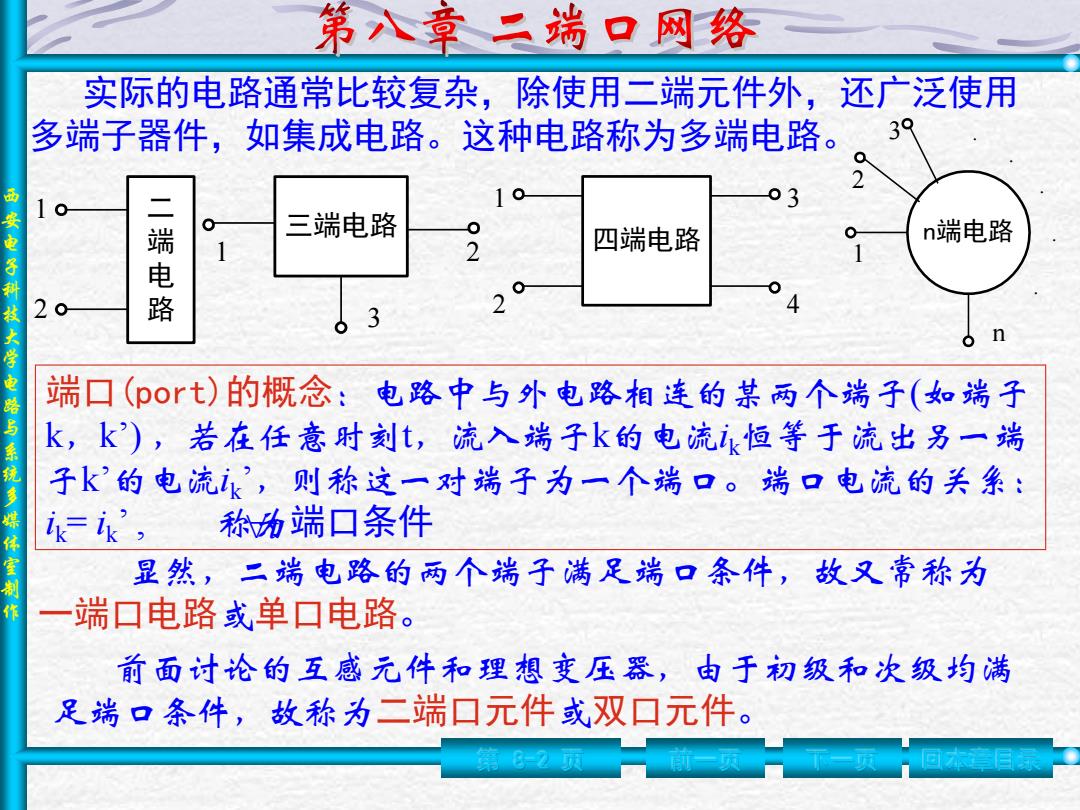
第八章二端口网络 实际的电路通常比较复杂,除使用二端元件外,还广泛使用 多端子器件,如集成电路。这种电路称为多端电路。 一安电子科技 三端电路 四端电路 n端电路 1 2 电路 2 3 大学电路与系统多媒体室制 端口(port)的概念: 电路中与外电路相连的某两个端子(如端子 k,k),若在任意时刻t,流入端子k的电流恒等于流出另一端 子k的电流,则称这一对端子为一个端口。端口电流的关系: =i', 称h端口条件 显然,二端电路的两个端子满足端口条件,故又常称为 端口电路或单口电路。 前面讨论的互感元件和理想变压器,由于初级和次级均满 足端口条件,故称为二端口元件或双口元件
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-2 页 前一页 下一页 回本章目录 二 端 电 路 1 2 三端电路 1 2 3 四端电路 1 2 3 4 n端电路 1 2 3 n · · · · · 显然,二端电路的两个端子满足端口条件,故又常称为 一端口电路或单口电路。 端口(port)的概念:电路中与外电路相连的某两个端子(如端子 k,k’) ,若在任意时刻t,流入端子k的电流ik恒等于流出另一端 子k’的电流ik ’,则称这一对端子为一个端口。端口电流的关系: ik= ik ’ , 称为 t 端口条件 前面讨论的互感元件和理想变压器,由于初级和次级均满 足端口条件,故称为二端口元件或双口元件。 实际的电路通常比较复杂,除使用二端元件外,还广泛使用 多端子器件,如集成电路。这种电路称为多端电路

第人章二瑞口网络 二端口电路或双口电路(two-port circuit)是研究多 端电路的基础。本章重点介绍描述二端口电路特性的 方法。 西安电子科技大学电路与系统多媒体室制作 1921年波里森(Brisig)首先提出二端口电路的概 念,指出:一个由线性元件组成的二端口电路,不论 其内部参数和结构如何,总可以用一组方程描述其外 部特性。他的这种黑箱方法目前已应用于许多领域。 8=8
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-3 页 前一页 下一页 回本章目录 二端口电路或双口电路(two-port circuit) 是研究多 端电路的基础。本章重点介绍描述二端口电路特性的 方法。 1921年波里森(Brisig)首先提出二端口电路的概 念,指出:一个由线性元件组成的二端口电路,不论 其内部参数和结构如何,总可以用一组方程描述其外 部特性。他的这种黑箱方法目前已应用于许多领域
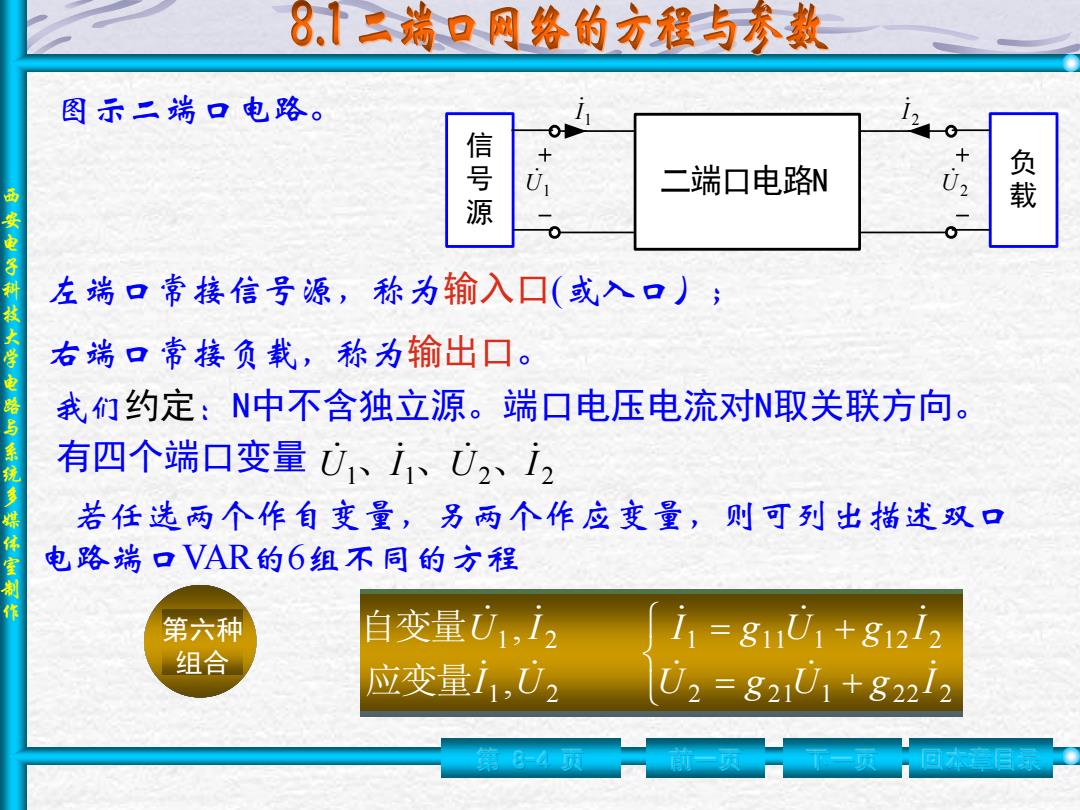
8.二端口网络的方程与参数 图示二端口电路。 信号源 二端口电路N 负载 西安电子科技大学电路与系统 左端口常接信号源,称为输入口(或入口); 右端口常接负载,称为输出口。 我们约定:N中不含独立源。端口电压电流对取关联方向。 有四个端口变量01、i、U2、i2 多媒体室制 若任选两个作自变量,另两个作应变量,则可列出描述双口 电路端口VAR的6组不同的方程 第六种 自变量01,i2 11=81U1+g1213 组合 应变量i1,U2 U2=g21U1+82212 8=4员
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-4 页 前一页 下一页 回本章目录 U1 二端口电路N U2 1 I 2 I 信 号 源 负 载 左端口常接信号源,称为输入口(或入口); 右端口常接负载,称为输出口。 我们约定:N中不含独立源。端口电压电流对N取关联方向。 有四个端口变量 1 1 2 2 U I U I 、 、 、 若任选两个作自变量,另两个作应变量,则可列出描述双口 电路端口VAR的6组不同的方程 第一种 组合 第二种三四五六 = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , U z I z I U z I z I U U I I 应变量 自变量 = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , I y U y U I y U y U I I U U 应变量 自变量 = + − − = + − ( ) ( ) , , 1 21 2 22 2 1 11 2 12 2 1 1 2 2 I a U a I U a U a I U I U I 应变量 自变量 = + − − = + − ( ) ( ) , , 2 2 1 1 2 2 1 2 1 1 1 1 2 1 2 2 1 1 I b U b I U b U b I U I U I 应变量 自变量 = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , I h I h U U h I h U U I I U 应变量 自变量 = + = + 2 2 1 1 2 2 2 1 1 1 1 1 2 2 1 2 1 2 , , U g U g I I g U g I I U U I 应变量 自变量 图示二端口电路
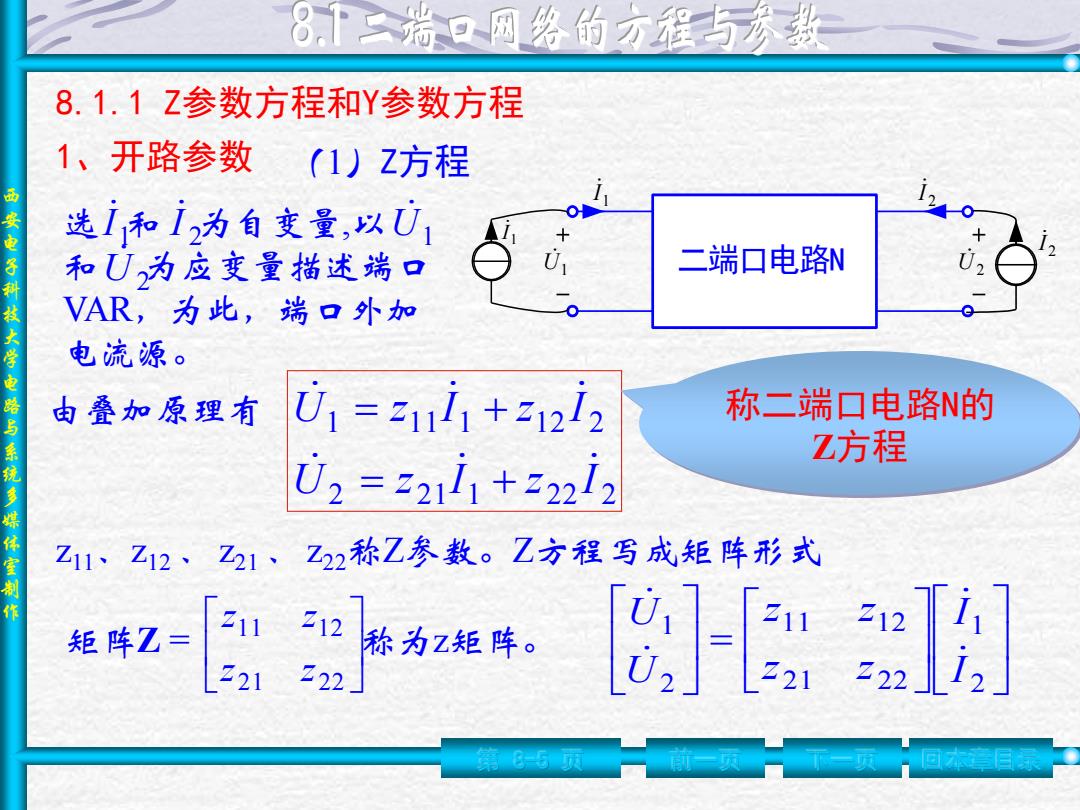
8「二瑞口网络的方程与秀数 8.1.1Z参数方程和Y参数方程 1、开路参数 (1)Z方程 西安电子科技大学电路与 选i和i2为自变量,以U1 和U为应变量描述端口 二端口电路N VAR,为此,端口外加 电流源。 由叠加原理有 ☑1=2111+3122 称二端口电路N的 系统 Z方程 02=221i1+32i2 多媒体室制作 Z11Z12、Z21、Z22称Z参数。乙方程写成矩阵形式 矩阵Z= 211212 称为z矩阵。 221 222」 - 5页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-5 页 前一页 下一页 回本章目录 8.1.1 Z参数方程和Y参数方程 1、开路参数 U1 二端口电路N U2 1 I 2 I 1 I 2 I 选 和 为自变量 ,以 和 为应变量描述端口 VAR,为此,端口外加 电流源。 1 I 2 I U1 U2 由叠加原理有 2 21 1 22 2 1 11 1 12 2 U z I z I U z I z I = + = + 称二端口电路N的 Z方程 z11、z12 、z21 、z22称Z参数。Z方程写成矩阵形式 = 2 1 21 22 11 12 2 1 I I z z z z U U 矩阵Z = 称为z矩阵。 21 22 11 12 z z z z (1)Z方程
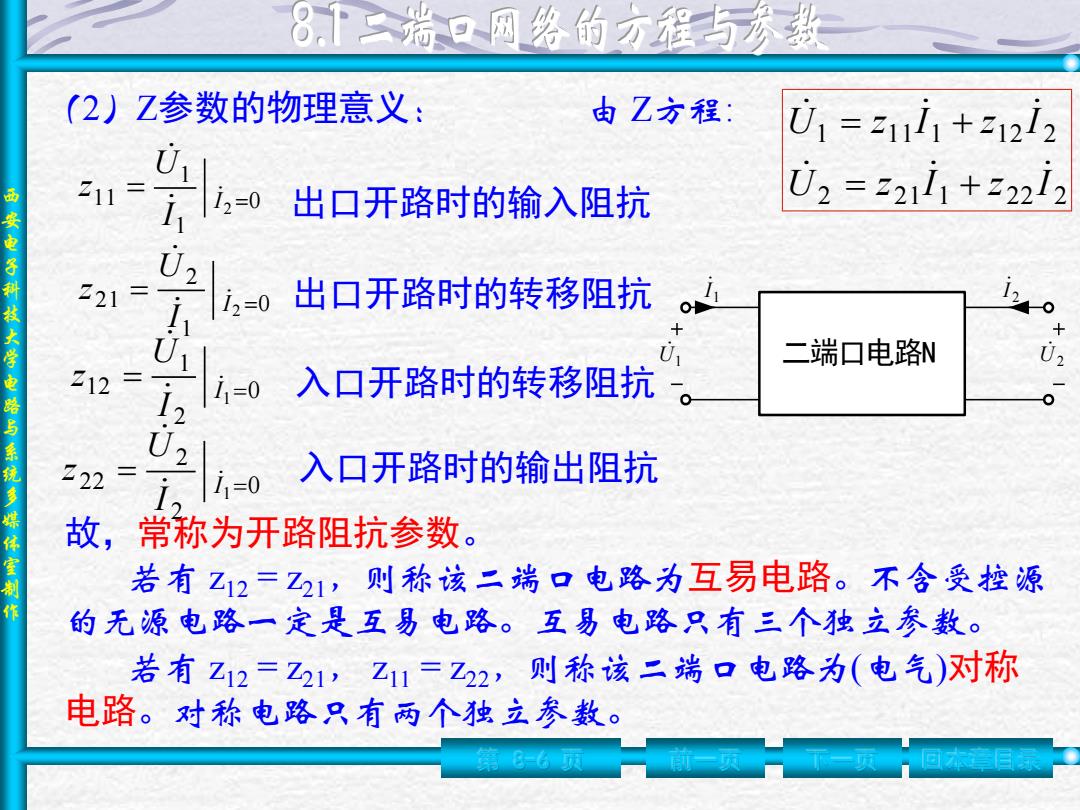
8「二瑞口网您的方程与秀数 (2)Z参数的物理意义: 由Z方程: 01=211i1+21212 U 西 211= i2=0 出口开路时的输入阻抗 02=321i1+z22i2 安电子科技大学电路与系统多媒体室制 02 221= i2=0 出口开路时的转移阻抗 U 二端口电路N 212 1-0 入口开路时的转移阻抗 U2 Z22 i=0 入口开路时的输出阻抗 故, 常称为开路阻抗参数。 若有乙12=Z21,则称该二端口电路为互易电路。不含受控源 的无源电路一定是互易电路。互易电路只有三个独立参数。 若有Z12=Z21,Z11=Z22,则称该二端口电路为(电气)对称 电路。对称电路只有两个独立参数
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-6 页 前一页 下一页 回本章目录 由 Z方程: 0 1 1 11 2 = = I I U z 出口开路时的输入阻抗 0 1 2 21 2 = = I I U z 出口开路时的转移阻抗 0 2 1 12 1 = = I I U z 入口开路时的转移阻抗 0 2 2 22 1 = = I I U z 入口开路时的输出阻抗 故,常称为开路阻抗参数。 (2)Z参数的物理意义: 2 21 1 22 2 1 11 1 12 2 U z I z I U z I z I = + = + 若有 z12 = z21,则称该二端口电路为互易电路。不含受控源 的无源电路一定是互易电路。互易电路只有三个独立参数。 若有 z12 = z21, z11 = z22,则称该二端口电路为(电气)对称 电路。对称电路只有两个独立参数。 U1 二端口电路N U2 1 I 2 I
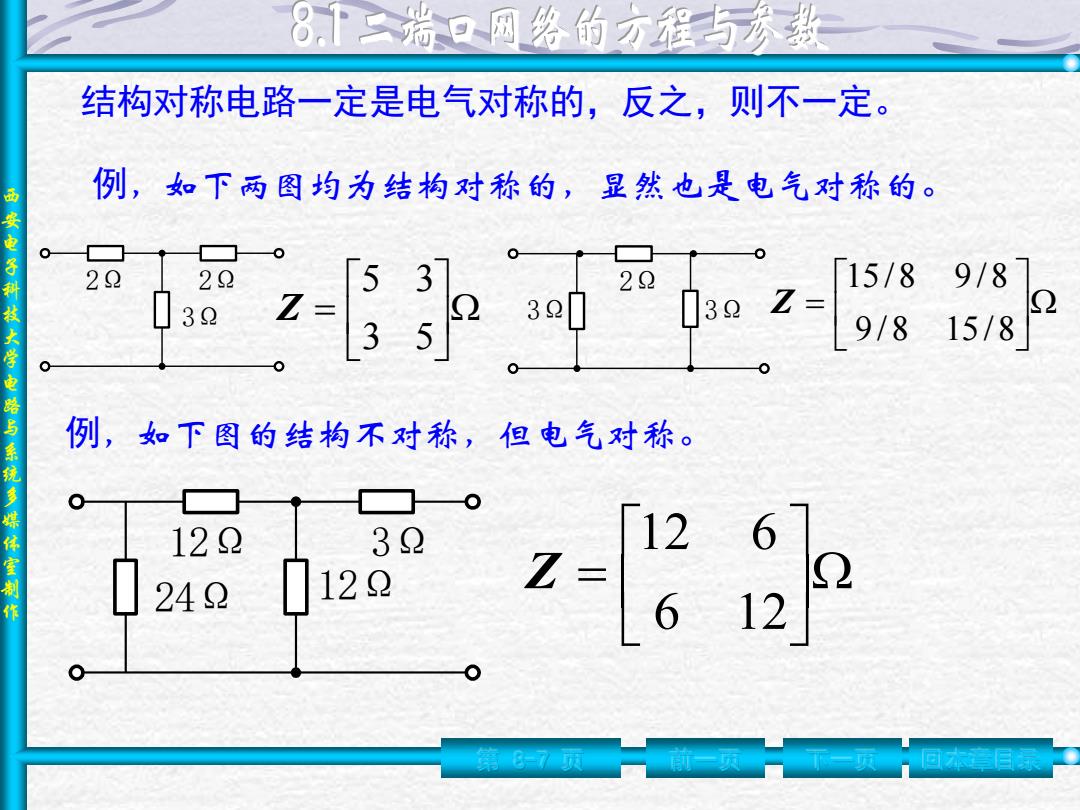
8「二瑞口网络的方程与参数 结构对称电路一定是电气对称的,反之,则不一定。 例,如下两图均为结构对称的,显然也是电气对称的。 一安电子科技大学电路与系统多媒体室制作 22 22 9/8 0 15/8 30 例,如下图的结构不对称,但电气对称。 ☐0 122 32 12 6 249 0129 Z= 6 12 87页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-7 页 前一页 下一页 回本章目录 结构对称电路一定是电气对称的,反之,则不一定。 例,如下两图均为结构对称的,显然也是电气对称的。 2Ω 2Ω 3Ω 2Ω 3Ω 3Ω = 3 5 5 3 Z = 9 /8 15/8 15/8 9 /8 Z 例,如下图的结构不对称,但电气对称。 12Ω 24Ω 12Ω 3Ω = 6 12 12 6 Z
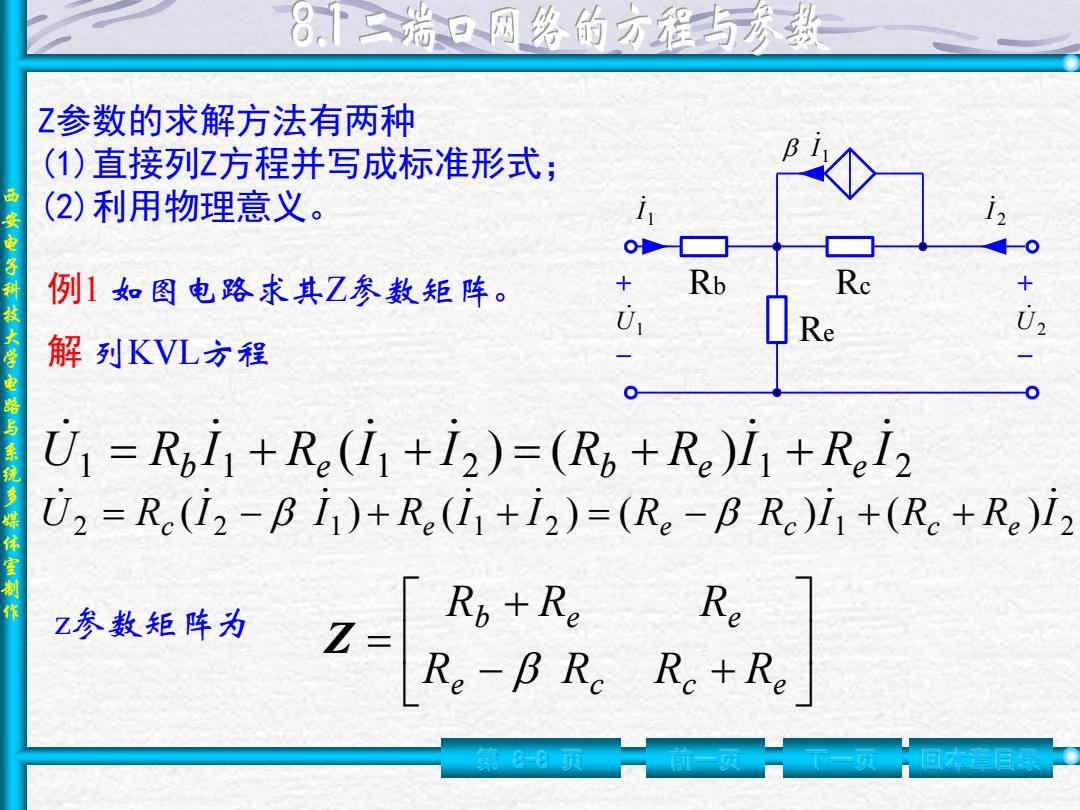
8下二瑞口网络的方程与秀数 Z参数的求解方法有两种 (1)直接列z方程并写成标准形式; (2)利用物理意义。 西安电子科技大学电路与系统多媒体室制作 例1如图电路求其Z参数矩阵。 Rb Re 01 Re 解列KVL方程 U=Rpi+Re(i+i2)=(Rp+Re)i+Rei2 U2=R(I2-BI1)+Re(I1+12)=(R。-BRc)I1+(R。+Re)I2 Z参数矩阵为 Ro+Re Re Z= Re-BR。Rc+Re 86页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-8 页 前一页 下一页 回本章目录 例1 如图电路求其Z参数矩阵。 U1 U2 1 I 2 I 1 I Rb Re Rc 解 列KVL方程 1 1 1 2 1 2 U R I R (I I ) (R R )I R I b e b e e = + + = + + 2 2 1 1 2 1 2 U R (I I ) R (I I ) (R R )I (R R )I c e e c c e = − + + = − + + z参数矩阵为 − + + = e c c e b e e R R R R R R R Z Z参数的求解方法有两种 (1)直接列Z方程并写成标准形式; (2)利用物理意义
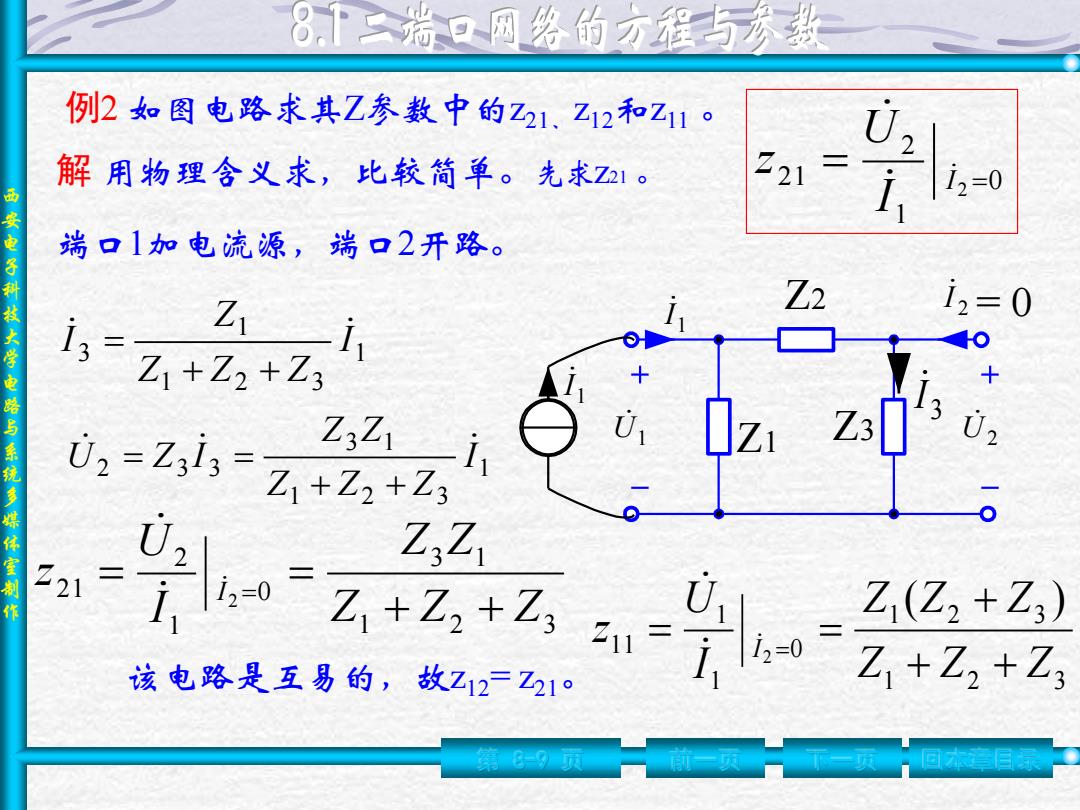
8「一瑞口网络的方程与秀数 例2如图电路求其Z参数中的Z21.Z12和Z11。 解用物理含义求,比较简单。先求Z21。 21 -0 端口1如电流源,端口2开路。 西安电子科技大学电路与系统多媒体室制 一i Z Z2 12=0 13 Z1+Z2+Z3 U2=Z3l3= Z3Z +2+石 I Z21 02 Z(Z2+Z3) 该电路是互易的,故Z12Z210 Z +Z,Z3 8-9页
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-9 页 前一页 下一页 回本章目录 U1 U2 1 I 2 I Z1 Z2 Z3 1 I = 0 解 用物理含义求,比较简单。先求z21 。 端口1加电流源,端口2开路。 1 1 2 3 1 3 I Z Z Z Z I + + = 3 I 1 1 2 3 3 1 2 3 3 I Z Z Z Z Z U Z I + + = = 1 2 3 3 1 0 1 2 2 1 2 Z Z Z Z Z I U z I + + = = = 该电路是互易的,故z12= z21。 例2 如图电路求其Z参数中的z21、z12和z11 。 0 1 2 21 2 = = I I U z 1 2 3 1 2 3 0 1 1 1 1 ( ) 2 Z Z Z Z Z Z I U z I + + + = = =
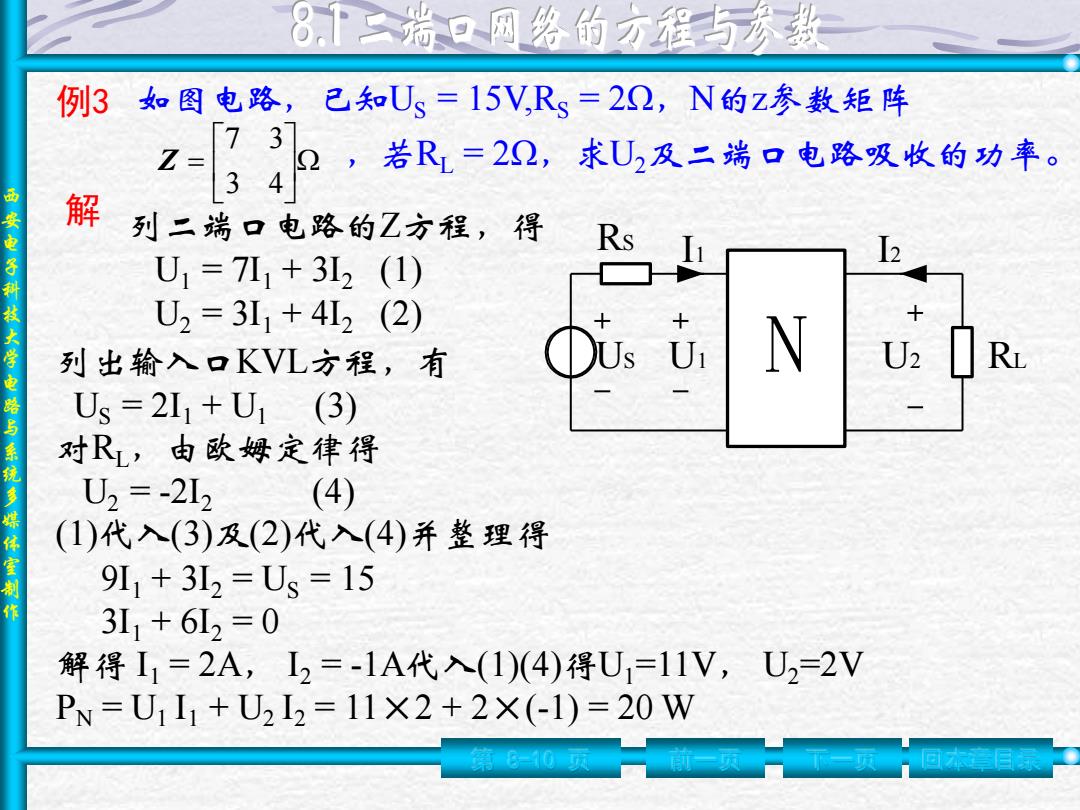
8下二瑞口网络的方程与参数 例3如图电路, 己知Us=15V,Rs=22,N的z参数矩阵 73 Z= 2,若R=22,求U2及二端口电路吸收的功率。 34 解 列二端口电路的Z方程,得 Rs U1=7L1+3L2(1) 一安电子科技大学电路与系统多媒体室制作 U2=3L1+4L2(2) 列出输入口KVL方程,有 U U2 Us=2I1+U1(3) 对R,由欧姆定律得 U2=-212 (4) (1)代入(3)及(2)代入(4)并整理得 9L1+3L2=Us=15 3L1+6L2=0 解得I1=2A,I2=-1A代入(1)(4)得U1=11V,U2=2V PN=U1I1+U2I2=11×2+2×(-1)=20W
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 8-10 页 前一页 下一页 回本章目录 例3 如图电路,已知US = 15V,RS = 2Ω,N的z参数矩阵 = 3 4 7 3 Z ,若RL = 2Ω,求U2及二端口电路吸收的功率。 解 列二端口电路的Z方程,得 U1 = 7I1 + 3I2 (1) U2 = 3I1 + 4I2 (2) 列出输入口KVL方程,有 US = 2I1 + U1 (3) 对RL,由欧姆定律得 U2 = -2I2 (4) (1)代入(3)及(2)代入(4)并整理得 9I1 + 3I2 = US = 15 3I1 + 6I2 = 0 解得 I1 = 2A, I2 = -1A代入(1)(4)得U1=11V, U2=2V PN = U1 I1 + U2 I2 = 11×2 + 2×(-1) = 20 W US N RS U1 U2 I1 I2 RL