
第9章现代数字调制解调技术 9.1正交振幅调制QAM① 9.2最小移频键控MSK 9.3高斯最小移频键控(GMSK 9.4 DOPSK调制 9.5OFDM调制 9.6扩频调制 9.7数字化接收技术 返回主目录
9.1 正交振幅调制(QAM) 9.2 最小移频键控(MSK) 9.3 高斯最小移频键控(GMSK) 9.4 DQPSK调制 9.5 OFDM调制 9.6 扩频调制 9.7 数字化接收技术 第 9 章 现代数字调制解调技术 返回主目录

第9章现代数字调制解调技术 9.1正交振幅调制(QA① 在现代通信中,提高频谱利用率一直是人们关注的焦点之 一。 近年来,随着通信业务需求的迅速增长,寻找频谱利用率 高的数字调制方式已成为数字通信系统设计、研究的主要目标 之一。正交振幅调制 QAM(Quadrature Amplitude Modulation) 就是一种频谱利用率很高的调制方式,其在中、大容量数字微 波通信系统、有线电视网络高速数据传输、卫星通信系统等领 域得到了广泛应用。在移动通信中,随着微蜂窝和微微蜂窝的 出现,使得信道传输特性发生了很大变化。过去在传统蜂窝系 统中不能应用的正交振幅调制也引起人们的重视
第 9 章 现代数字调制解调技术 9.1正交振幅调制(QAM) 在现代通信中,提高频谱利用率一直是人们关注的焦点之 一。近年来,随着通信业务需求的迅速增长,寻找频谱利用率 高的数字调制方式已成为数字通信系统设计、研究的主要目标 之一。 QAM(Quadrature Amplitude Modulation) 就是一种频谱利用率很高的调制方式,其在中、 大容量数字微 波通信系统、有线电视网络高速数据传输、卫星通信系统等领 域得到了广泛应用。在移动通信中,随着微蜂窝和微微蜂窝的 出现,使得信道传输特性发生了很大变化。 过去在传统蜂窝系 统中不能应用的正交振幅调制也引起人们的重视

9.1.1MOAM调制原理 正交振幅调制是用两个独立的基带数字信号对两个相互正 交的同频载波进行抑制载波的双边带调制,利用这种已调信号 在同一带宽内频谱正交的性质来实现两路并行的数字信息传输 正交振幅调制信号的一般表示式为 SMQAM(t)= ∑Ang(t-nTs)cos(wt+9n) n 式中,An是基带信号幅度,g(t-nT)是宽度为T的单个基带 信号波形。式(9.1-1)还可以变换为正交表示形式: SMQAM(t)= >4g(t-nTs)cos(wt+9)
9.1.1 MQAM 正交振幅调制是用两个独立的基带数字信号对两个相互正 交的同频载波进行抑制载波的双边带调制,利用这种已调信号 在同一带宽内频谱正交的性质来实现两路并行的数字信息传输。 正交振幅调制信号的一般表示式为 sMQAM(t)= ( )cos( ) S c n n n A g t − nT w t + 式中,An是基带信号幅度,g(t-nTs )是宽度为Ts的单个基带 信号波形。 式(9.1 - 1)还可以变换为正交表示形式: sMQAM(t)= ( )cos( ) S c n n n A g t − nT w t +

SMQAM(t)=[4g(t-nTs)cos9,]coswt-[4g(t-nTs)sin 9]sin w.t 令 Xn-An cospn Yn-Ansinon 则式(9.1-2)变为 SMOAM(t)=[>Xg(t-nTs)cos9]coswt-[>Y,g(t-nTs)sin 9,]sin w. =X(t)cosw t-y(t)sin wt QAM中的振幅X和Y可以表示为 Xn-CnA Y=dA
A g t nT w t A g t nT w t S n c n S n c n n n sMQAM(t)= [ ( − )cos ]cos −[ ( − )sin ]sin 令 Xn=An cosφn Yn=An sinφn 则式(9.1 - 2)变为 sMQAM(t)= X g t nT w t Y g t nT w t S n c n S n c n n n [ ( − )cos ]cos −[ ( − )sin ]sin X t w t y t w t c c = ( )cos − ( )sin QAM中的振幅Xn和Yn可以表示为 Xn=cnA Yn=dnA

式中,A是固定振幅,cn、dn由输入数据确定。cn、dn决 定了已调QAM信号在信号空间中的坐标点。 QAM信号调制原理图如图9·1所示。图中,输入的二 进制序列经过串/并变换器输出速率减半的两路并行序列, 再分别经过2电平到L电平的变换,形成L电平的基带信号。 为了抑制已调信号的带外辐射,该L电平的基带信号还要经 过预调制低通滤波器,形成X()和Y(),再分别对同相载波和 正交载波相乘。最后将两路信号相加即可得到QAM信号
式中,A是固定振幅,cn、dn由输入数据确定。cn、dn决 定了已调QAM信号在信号空间中的坐标点。 QAM信号调制原理图如图 9 - 1 所示。图中,输入的二 进制序列经过串/并变换器输出速率减半的两路并行序列, 再分别经过2电平到L电平的变换,形成L电平的基带信号。 为了抑制已调信号的带外辐射,该L电平的基带信号还要经 过预调制低通滤波器,形成X(t)和Y(t),再分别对同相载波和 正交载波相乘。 最后将两路信号相加即可得到QAM信号
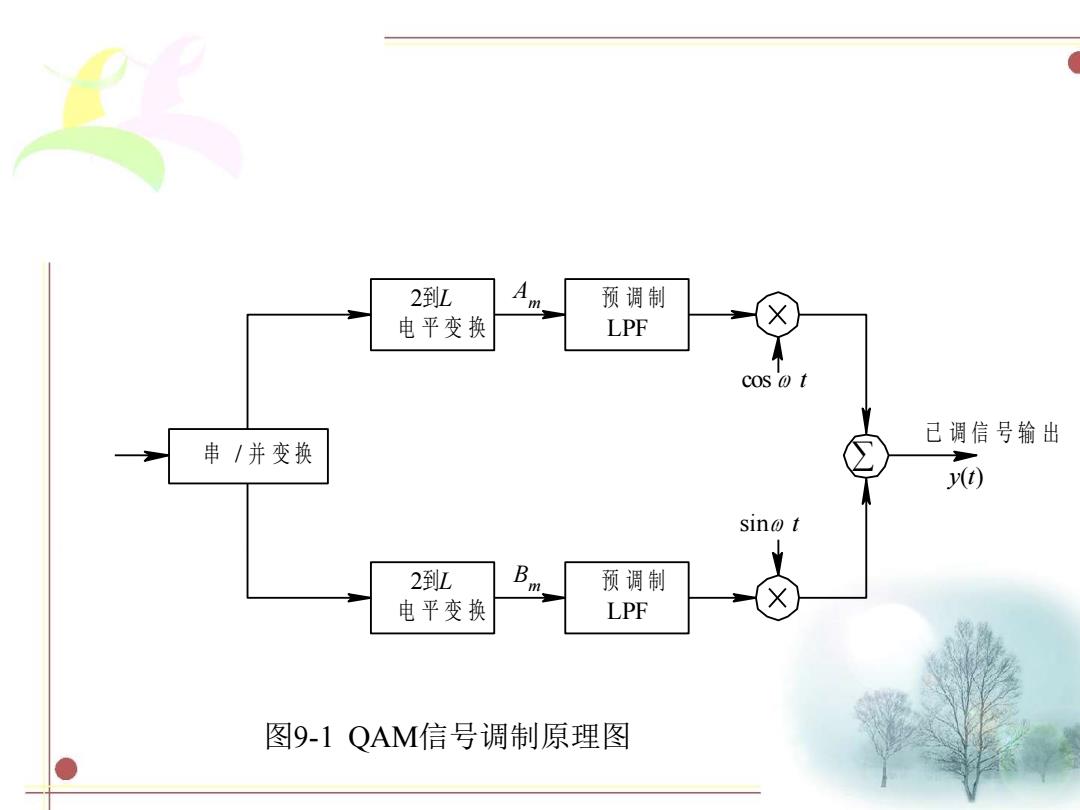
2到L A m 预调制 电平变换 LPF cos o t 己调信号输出 串/并变换 y(t) sino t 2到L B m 预调制 电平变换 LPF 图9-1QAM信号调制原理图
图9-1 QAM信号调制原理图 2到L 电 平 变 换 2到L 电 平 变 换 预 调 制 LPF 预 调 制 LPF 串 / 并 变 换 cos t sin t Am Bm y(t) 已 调 信 号 输 出 ∑

信号矢量端点的分布图称为星座图。通常,可以用星座 图来描述QAM信号的信号空间分布状态。对于M=16的 16QAM来说,有多种分布形式的信号星座图。两种具有代 表意义的信号星座图如图9-2所示。在图9-2(a)中,信号 点的分布成方型,故称为方型16QAM星座,也称为标准型 16QAM。在图9-2(b)中,信号点的分布成星型,故称为星 型16QAM星座。 若信号点之间的最小距离为2A,且所有信号点等概率 出现,则平均发射信号功率为 君c-的 M
信号矢量端点的分布图称为星座图。通常,可以用星座 图来描述QAM信号的信号空间分布状态。对于M=16 16QAM来说,有多种分布形式的信号星座图。 两种具有代 表意义的信号星座图如图 9 - 2 所示。在图 9 - 2(a)中, 信号 点的分布成方型,故称为方型16QAM星座,也称为标准型 16QAM。在图 9 - 2(b)中,信号点的分布成星型,故称为星 型16QAM星座。 若信号点之间的最小距离为2A,且所有信号点等概率 出现,则平均发射信号功率为 ( ) ( ) 2 1 2 2 n M n cn d M A p s = + =
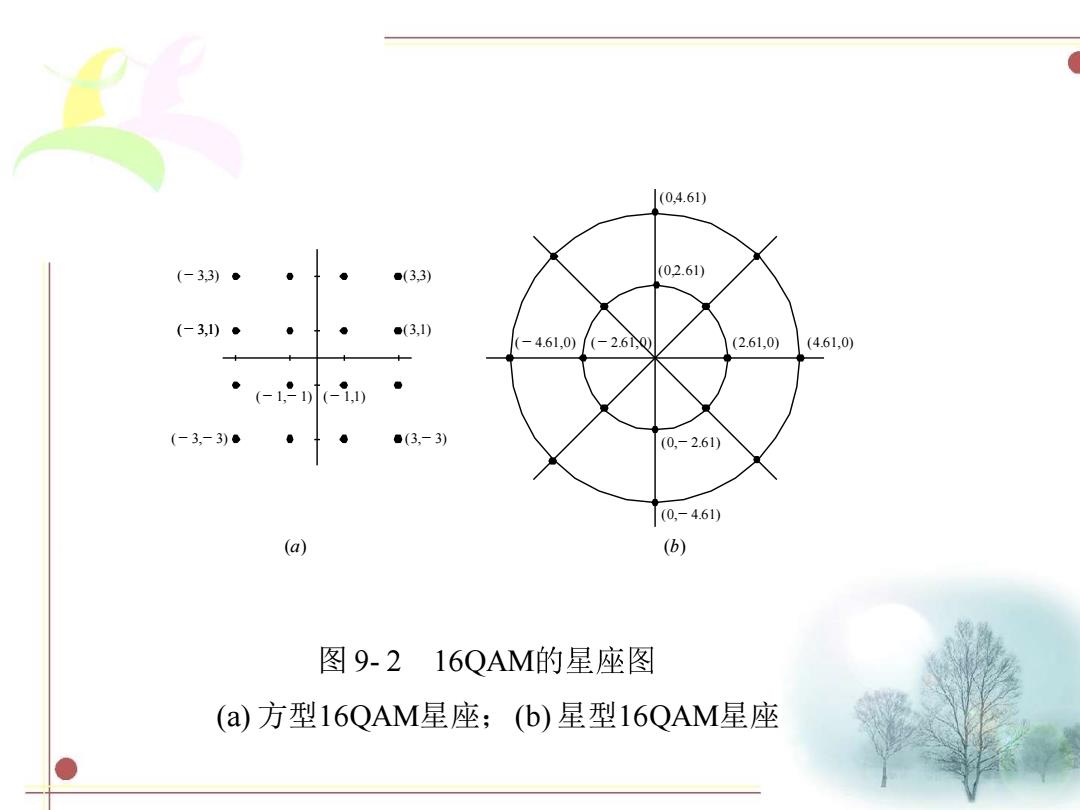
(0,4.61) (-3,3)● ●(3,3) (02.61) (-3,1)。 ●(3.1) (-4.61,0) /(-2.6100 (2.61,0) (4.61,0) ·-2-i (-3,-3)·· ●(3,-3) (0,-2.61) (0,-4.61) (a) (b) 图9-216QAM的星座图 (a)方型16QAM星座;(b)星型16QAM星座
图 9- 2 16QAM (a) 方型16QAM星座;(b) 星型16QAM星座 (- 4.61,0) (- 2.61,0) (2.61,0) (4.61,0) (0,2.61) (0,4.61) (0,- 4.61) (0,- 2.61) (- 3,3) (- 3,1) (- 3,- 3) (3,- 3) (3,1) (3,3) (- 1,- 1) (- 1,1) (a) (b)

对于方型16QAM,信号平均功率为 x)=( n=1 对于星型16QAM,信号平均功率为 p(S)= 2C:哈)名426r+sx46n3f n= 两者功率相差1.4dB。另外,两者的星座结构也有重要的 差别。一是星型16QAM只有两个振幅值,而方型16QAM 有三种振幅值;二是星型16QAM只有8种相位值,而方型 16QAM有12种相位值。这两点使得在衰落信道中,星型 16QAM比方型16QAM更具有吸引力
对于方型16QAM,信号平均功率为 2 2 2 1 2 2 (4 2 8 10 4 18) 10 16 ( ) ( ) A A c d M A p s n M n = n + = + + = = 对于星型16QAM,信号平均功率为 2 2 2 2 2 1 2 2 (4 2.61 8 4.61 ) 14.03 16 ( ) ( ) A A c d M A p s n M n = n + = + = = 两者功率相差1.4dB。另外,两者的星座结构也有重要的 差别。一是星型16QAM只有两个振幅值,而方型16QAM 有三种振幅值;二是星型16QAM只有8种相位值,而方型 16QAM有12种相位值。这两点使得在衰落信道中,星型 16QAM比方型16QAM更具有吸引力

M=4,16,32,,256时 MQAM信号的星座图如图9-3 所示。其中,M=4,16,64,256时星座图为矩形,而M=32,128 时星座图为十字形。前者M为2的偶次方,即每个符号携带偶 数个比特信息;后者M为2的奇次方,即每个符号携带奇数个 比特信息。 若已调信号的最大幅度为1,则MPSK信号星座图上信号 点间的最小距离为 π dMPsK=2 sin M 而MQAM信号矩形星座图上信号点间的最小距离为
M=4, 16, 32, …, 256 MQAM 信号的星座图如图 9 - 3 所示。其中,M=4, 16, 64, 256 时星座图为矩形,而M=32, 128 时星座图为十字形。前者M为2的偶次方,即每个符号携带偶 数个比特信息;后者M为2的奇次方,即每个符号携带奇数个 比特信息。 若已调信号的最大幅度为1,则MPSK信号星座图上信号 点间的最小距离为 dMPSK =2 sin M 而MQAM信号矩形星座图上信号点间的最小距离为