
主要内容 第八章数字信号的最佳接收 ·1、引言 。 6、起伏信号的最佳 0 2、数字信号接收的 接收 统计表述 。7、普通接收机与最 ·3、关于最佳接收的 佳接收机的性能比较 准则 ·8、匹配滤波器 ·4、确知信号的最佳 接收 ·9、最佳基带传输系 ·5、随相信号的最佳 统 接收
第八章 数字信号的最佳接收 • 1、引言 • 2、数字信号接收的 统计表述 • 3、关于最佳接收的 准则 • 4、确知信号的最佳 接收 • 5、随相信号的最佳 接收 • 6、起伏信号的最佳 接收 • 7、普通接收机与最 佳接收机的性能比较 • 8、匹配滤波器 • 9、最佳基带传输系 统 ● —— 主要内容

8.1引言 通信系统中信道特性不理想及信道噪声 的存在,直接影响接收系统的性能, 而一个通信系统的质量优劣在很大程度 上取决于接收系统的性能
8.1 引言 通信系统中信道特性不理想及信道噪声 的存在,直接影响接收系统的性能, 而一个通信系统的质量优劣在很大程度 上取决于接收系统的性能

研究对象 接收问题 研究从噪声中如何最好地提取有用信号,且在某个 准则下构成最佳接收机,使接收性能达到最佳,这 就是最佳接收理论。 研究的问题 最佳接收或信号接收最佳化的问题
研究从噪声中如何最好地提取有用信号,且在某个 准则下构成最佳接收机,使接收性能达到最佳,这 就是最佳接收理论。 研究对象 接收问题 研究的问题 最佳接收或信号接收最佳化的问题

前面分析的问题是 给出接收机模型然后分析其性能 现在讨论的问题是 从数字信号接收统计模型出 发,依据某种最佳接收准则, 推导出相应的最佳接收机结 构,然后再分析其性能
从数字信号接收统计模型出 发,依据某种最佳接收准则, 推导出相应的最佳接收机结 构,然后再分析其性能。 前面分析的问题是 给出接收机模型然后分析其性能 现 在 讨 论 的 问 题 是

8.2数字信号接收的统计表述 带噪声的数字信号的接收,实质上是一 个统计接收问题 也可以说数字信号接收过程是一个统计 判决过程。从统计学的观点来看,数字 信号接收可以用一个统计模型来表述
8.2 数字信号接收的统计表述 带噪声的数字信号的接收,实质上是一 个统计接收问题, 也可以说数字信号接收过程是一个统计 判决过程。从统计学的观点来看,数字 信号接收可以用一个统计模型来表述
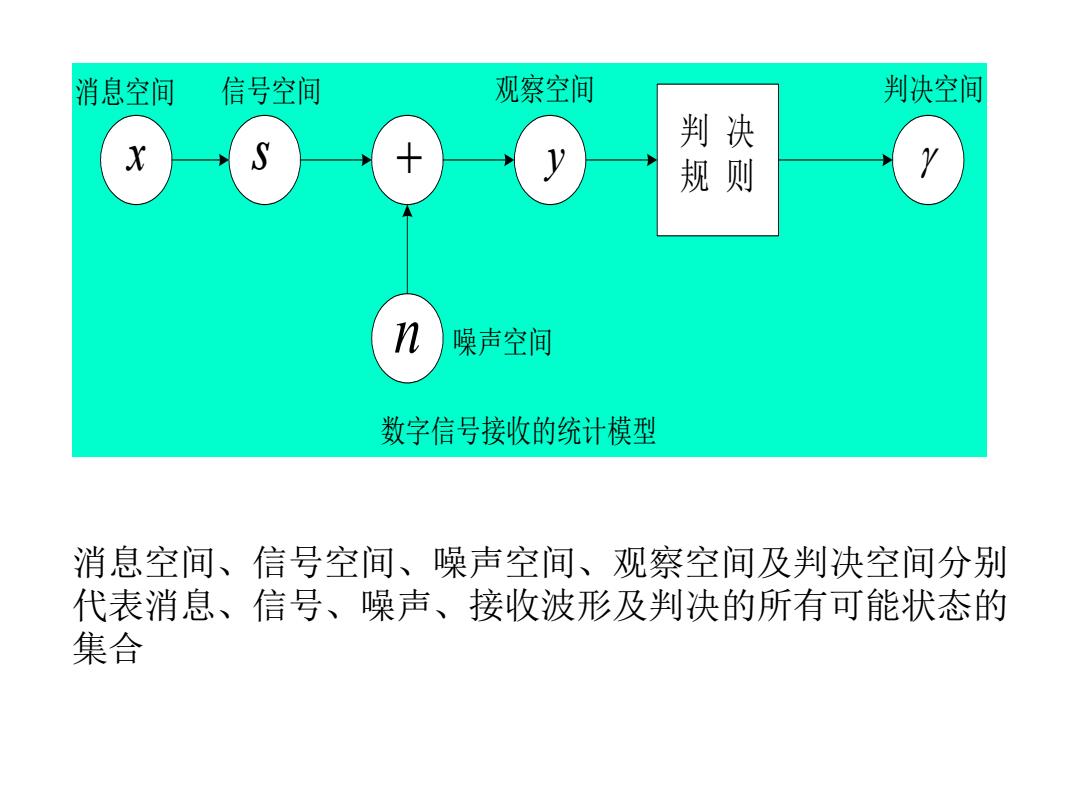
消息空间 信号空间 观察空间 判决空间 判决 X S 规则 n 噪声空间 数字信号接收的统计模型 消息空间、信号空间、噪声空间、观察空间及判决空间分别 代表消息、信号、噪声、接收波形及判决的所有可能状态的 集合
x s + y n 判 决 规 则 消息空间 信号空间 观察空间 判决空间 噪声空间 数字信号接收的统计模型 消息空间、信号空间、噪声空间、观察空间及判决空间分别 代表消息、信号、噪声、接收波形及判决的所有可能状态的 集合

在数字通信系统中,消息是离散的状态,设消息的 状态集合为 X={x1,X2,,xm} 若消息集合中每一状态的发送是统计独立的,第个 状态x的出现概率为P(x), 则消息X的一维概率分布为 Xj X2 Xm P(X1)P(X2). P(Xm) 根据概率的性质有 ∑p(x)=1
在数字通信系统中, 消息是离散的状态, 设消息的 状态集合为 X={x1 , x2 , …, xm} 若消息集合中每一状态的发送是统计独立的, 第i个 状态xi的出现概率为P(xi ), 则消息X的一维概率分布为 X1 x2 … xm P(x1 ) P(x2 ) … P(xm) 根据概率的性质有 1 ( ) 1 m i i p x = =

若消息各状态x1,x2,,Xm出现的概率相等,则有 1 P(x)=P(x2)=…=P(xm)= m 消息是各种物理量,本身不能直接在数字通信系统 中进行传输 因此 需要将消息变换为相应的电信号s(),用参数$来表示
若消息各状态x1 , x2 , …, xm出现的概率相等,则有 1 2 1 ( ) ( ) ( ) P x P x P xm m = = = = 消息是各种物理量, 本身不能直接在数字通信系统 中进行传输 需要将消息变换为相应的电信号s(t),用参数S来表示。 因此

将消息变换为信号可以有各种不同的变换关系, 通常最直接的方法是建立消息与信号之间一一对 应的关系,即消息x与信号s(=1,2,,m)相对 应。 这样,信号集合S也由m个状态所组成 即 S={S1,S2,,Sm}
将消息变换为信号可以有各种不同的变换关系, 通常最直接的方法是建立消息与信号之间一一对 应的关系,即消息xi与信号si (i=1, 2, …, m)相对 应。 这样,信号集合S也由m个状态所组成 即 S={s1 , s2 , …, sm}

并且信号集合各状态出现概率与消息集合各状 态出现概率相等,即 P(s)=P(x) P(S2)=P(x2) P(Sm)=P(xm) 同时也有 ∑ps,)=1 i1
并且信号集合各状态出现概率与消息集合各状 态出现概率相等,即 1 1 2 2 ( ) ( ) ( ) ( ) P s P x P s P x = = ( ) ( ) P s P x m m = . . . 同时也有 = = n i i p s 1 ( ) 1