
第五章动态电路的时域分析 5.1动态电路的方程及其解 5.5一阶电路的全响应— 一、动态电路方程的建立 三要素公式一 二、微分方程的经典解法 ◆ 5.6一阶电路的阶跃响应 西安电子科技大学电路与系统多媒体室制作 5.2 电路的初始值 一、阶跃函数 一、 独立初初始值 二、阶跃响应 二、非独立初始值 5.7二阶电路分析 5.3一阶电路的零输入响应 一、零输入响应 与时间常数、 二、阶跃响应 5.4一阶电路的零状态响应 5.8正弦激励下一阶电路 的响应 点击目录心,进入相关章节
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 5.5 一阶电路的全响应—— 三要素公式 5.6 一阶电路的阶跃响应 一、阶跃函数 二、阶跃响应 5.7 二阶电路分析 一、零输入响应 二、阶跃响应 5.8 正弦激励下一阶电路 的响应 5.1 动态电路的方程及其解 一、动态电路方程的建立 二、微分方程的经典解法 5.2 电路的初始值 一、独立初初始值 二、非独立初始值 5.3 一阶电路的零输入响应 与时间常数 5.4 一阶电路的零状态响应 点击目录 ,进入相关章节 第 5-1 页 前一页 下一页 退出本章
5.1动态电路的方程及其解 动态电路方程的建立 由于动态电路中的电感电容的VAR是微积分关系,可以预料,动态电 路列出的方程一定是微积分方程。若描述电路的方程是一阶微分方程, 相应的电路称为一阶电路(first order circuit)。 电 1、依据:元件VAR,KCL和KV儿列写方程; 技 2、一阶电路举例: 学 例1:图RC电路,t=0时开关S闭合,讨 us 电路 论t>O时的电容电压uc()。 与 t>0时,根据KV儿方程列出回路电压方程为 RC串联电路 多 uR uc-us =0 duc duc 体 根据元件的VAR,有i=C UR=Ri=RC dt dt 作 代入上式,整理得 duc+ di RC uc us RC duc dt r 令x=RC,其单位是秒。因为[RC]=V/A[CW]=[C/A]=[] 故x称为时间常数,简称时常数
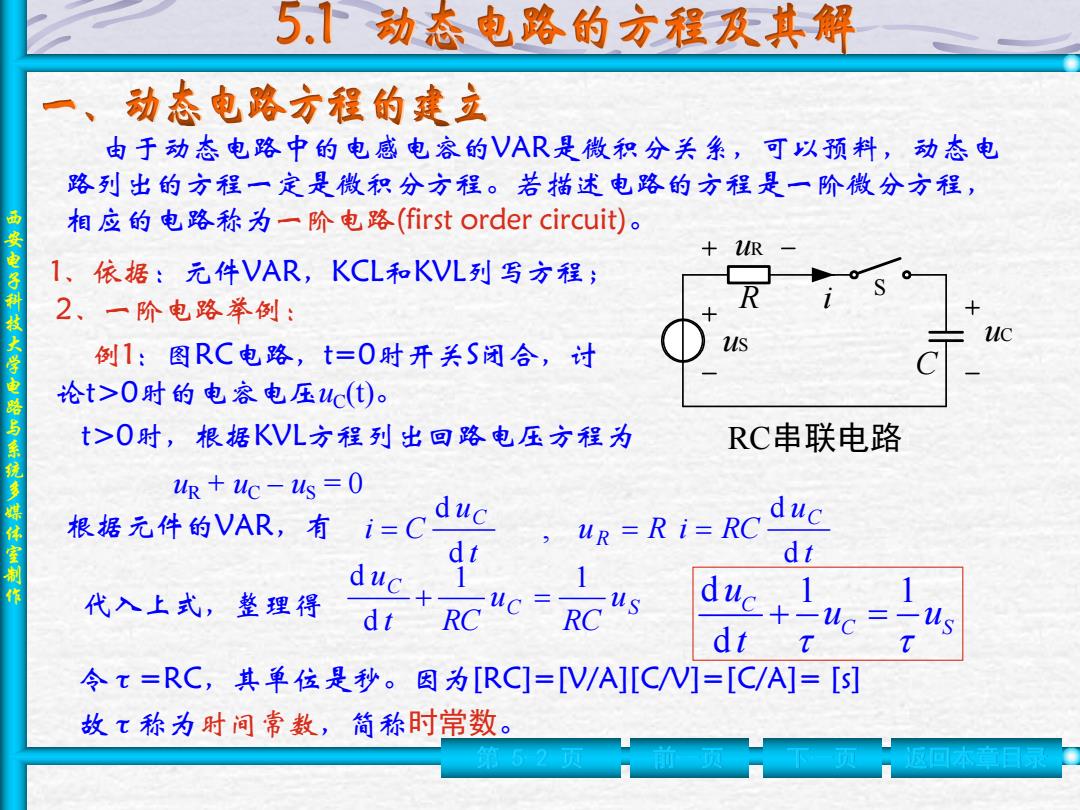
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 第 5-2 页 前一页 下一页 返回本章目录 1、依据:元件VAR,KCL和KVL列写方程; 2、一阶电路举例: 由于动态电路中的电感电容的VAR是微积分关系,可以预料,动态电 路列出的方程一定是微积分方程。若描述电路的方程是一阶微分方程, 相应的电路称为一阶电路(first order circuit)。 S uS uR uC R C i RC串联电路 例1:图RC电路,t=0时开关S闭合,讨 论t>0时的电容电压uC(t)。 t>0时,根据KVL方程列出回路电压方程为 uR + uC – uS = 0 根据元件的VAR,有 t u u R i RC t u i C C R C d d , d d 代入上式,整理得 C S C u RC u t RC u 1 1 d d 令τ=RC,其单位是秒。因为[RC]=[V/A][C/V]=[C/A]= [s] 故τ称为时间常数,简称时常数。 d 1 1 d C C S u u u t
5上动态电路的方程及共耀 动态路方程的瘦元 例2:图RL电路,t=0时开关S闭合,讨论t>0时的电感电流()。 t>O附,根据KCL有 is iR iR +it-is=0 R L L 西安电子科 根据元件的VAR,有 技大 diL uL=L uL_ L diL RL并联电路 dt iR= R R dt 电路与系统多媒体 代入上式,整理得 diL+ R R di+= dt L -=-1s dt 入 令x=LR,其单位是秒。因为L/R]=[Wb/A]/IV/A]=[Wb/V]=[s] 室制 故τ称为时间常数,简称时常数。 观察上两例列出的方程,除变量不同外,均为典型的一阶微分方程,因 此均为一阶电路。一阶微分方程的一般形式可写为 y(①)+ay)=bf(), 式中y()为响应,∫()为激动
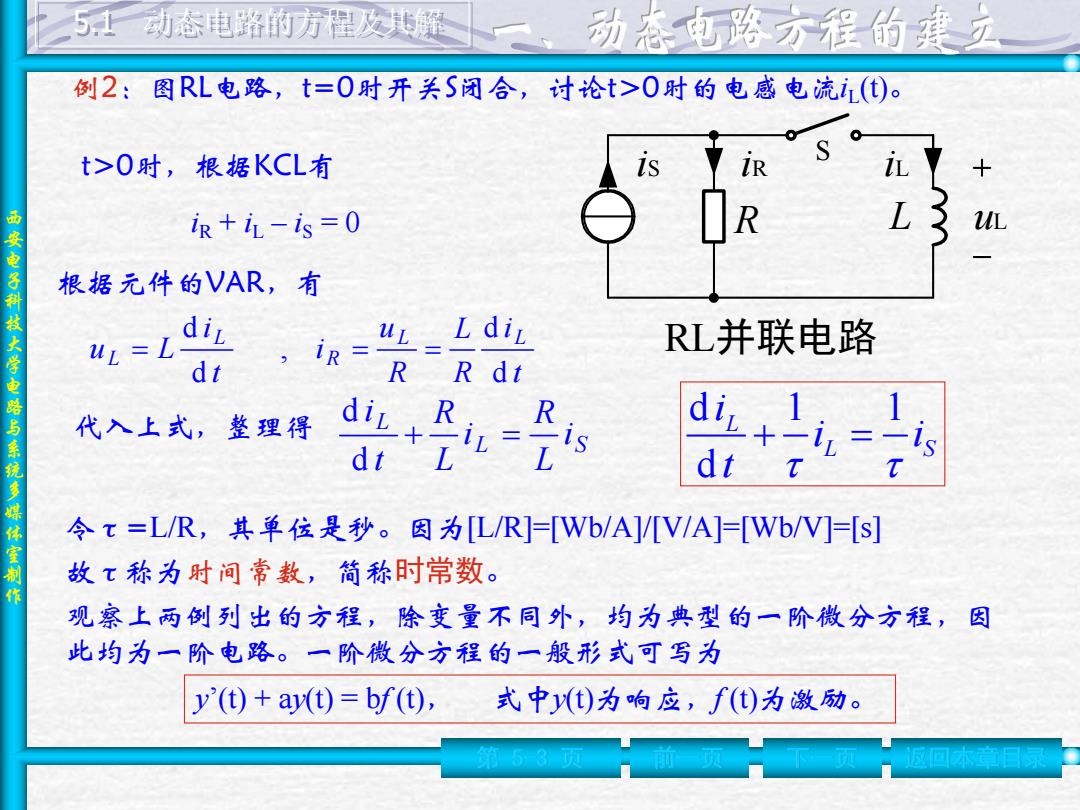
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 例2:图RL电路,t=0时开关S闭合,讨论t>0时的电感电流iL (t)。 第 5-3 页 前一页 下一页 返回本章目录 5.1 动态电路的方程及其解 RL并联电路 S iS iR iL R L uL t>0时,根据KCL有 iR + iL – iS = 0 根据元件的VAR,有 t i R L R u i t i u L L L R L L d d , d d 代入上式,整理得 L S L i L R i L R t i d d 观察上两例列出的方程,除变量不同外,均为典型的一阶微分方程,因 此均为一阶电路。一阶微分方程的一般形式可写为 y’(t) + ay(t) = bf (t), 式中y(t)为响应,f (t)为激励。 d 1 1 d L L S i i i t 令τ=L/R,其单位是秒。因为[L/R]=[Wb/A]/[V/A]=[Wb/V]=[s] 故τ称为时间常数,简称时常数
5上动态电路的方程及共解 动路方程的瓖元 3、二阶电路举例: +R +UL 例:图RLC串联电路,仍以电容电压(t)作 Y 为电路的响应。 染 根据KV儿方程有 电子 uR +ut uc-us =0 根据元件的VAR,有 学 路 i=cduc d-uc Ri-cuc dt 系统多 代入上式,整理得 de+Rde+e-i us 体 dt2 L dt LC 制 这是二阶微分方程,因此称该电路为二阶电路。二阶微分方程的一般形 式可写为 y'()+ay'()+a)=bf()
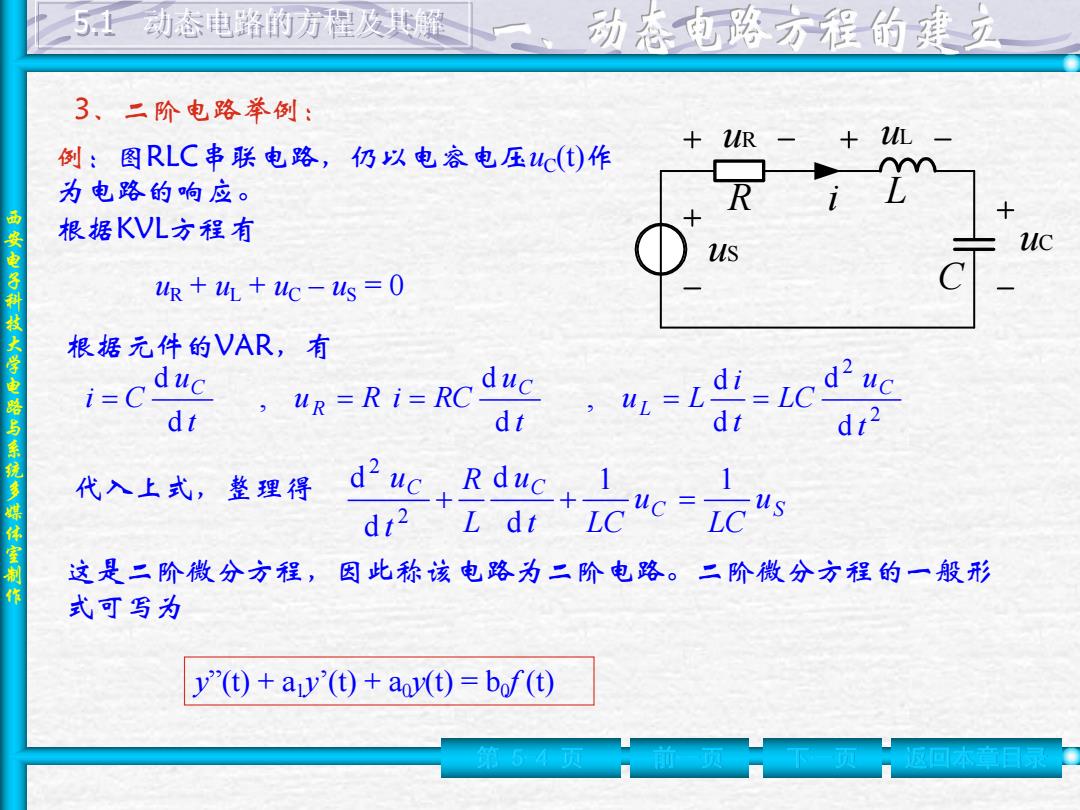
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3、二阶电路举例: 第 5-4 页 前一页 下一页 返回本章目录 例:图RLC串联电路,仍以电容电压uC(t)作 为电路的响应。 uS uR uC R C i uL L 根据KVL方程有 uR + uL + uC – uS = 0 根据元件的VAR,有 2 2 d d d d , d d , d d t u LC t i u L t u u R i RC t u i C C L C R C 代入上式,整理得 C S C C u LC u t LC u L R t u 1 1 d d d d 2 2 这是二阶微分方程,因此称该电路为二阶电路。二阶微分方程的一般形 式可写为 y”(t) + a1y’(t) + a0y(t) = b0 f (t) 5.1 动态电路的方程及其解

5上动态电路的方程及共解 一、动态路方程的元 4、建立动态方程的一般步骤 ()、根据电路建立KCL或KVL方程,写出各元 件的伏安关系; 西安电子科技大学电路与系统多媒体室制作 2)、在以上方程中消去中间变量,得到所需变 量的微分方程。 对于轻复杂的动态电路,常用拉普拉斯变换进 行分析。 第55页 区回本章日
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 4、建立动态方程的一般步骤 第 5-5 页 前一页 下一页 返回本章目录 ⑴、根据电路建立KCL或KVL方程,写出各元 件的伏安关系; ⑵、在以上方程中消去中间变量,得到所需变 量的微分方程。 对于较复杂的动态电路,常用拉普拉斯变换进 行分析。 5.1 动态电路的方程及其解

5上动态电路的方程及共耀 二、微分方程的经典解法 1、微分方程的经典解法 一阶和二阶微分方程一般形式为 y()+a)=bf() (1),y()+ay()+ao()=bf() (2) 西安电子 对于线性时不变动态电路,上式中的系数都是常数。 高等数学学过,线性常系数微分方程的解由两部分组成: 技大学 y()=yh(t)+y,() 即:完全解=齐次解(通解)+特解 路 齐次解y(①:它的函数形式取决于微分方程的特征根。 对于一阶微分方程,其特征方程为s+a=0,特征根为S=-a,故 与系统多媒体室制作 yh(t)=K est=K e-at 式中K为待定常数。 对于二阶微分方程,其特征方程为s2+a1S+a0=0,特征根为S1和S2, 当s1f2时,yh(①)=K1esIt+K2es2t 当s1=S2=s时,yh(t)=(K1+K2t)est 式中待定常数K、K2将在完全解中由初始条件确定
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 1、微分方程的经典解法 第 5-6 页 前一页 下一页 返回本章目录 5.1 动态电路的方程及其解 一阶和二阶微分方程一般形式为 y’(t) + ay(t) = bf (t) (1) , y”(t) + a1y’(t) + a0y(t) = b0 f (t) (2) 对于线性时不变动态电路,上式中的系数都是常数。 高等数学学过,线性常系数微分方程的解由两部分组成: y(t) = yh(t) + yp(t) 即:完全解 =齐次解(通解)+ 特解 齐次解yh(t) :它的函数形式取决于微分方程的特征根。 对于一阶微分方程,其特征方程为 s + a = 0,特征根为s = -a,故 yh(t) = K e st = K e -a t 式中K为待定常数。 对于二阶微分方程,其特征方程为 s 2 + a1s + a0 = 0,特征根为s1 和s2 , 当s1 ≠s2 时, yh(t) = K1 e s1t + K2 e s2t 当s1 = s2 = s时, yh(t) = (K1 + K2 t)e st 式中待定常数K1、 K2将在完全解中由初始条件确定
5上动态电路的方程及共耀 二、微分程的经典解房 特解y①):特解具有与激励f)相同的函数形式。列表如下:(P99表3-2) 激励F(t)函数形式 特解y() 直流 常数A 西安电子科技大学电路与系统多媒体室制作 tm Amtm+Am-itm-1+...+Ait Ao Aeat 当a不是特征根时 eat (At+Ao)eat 当a是特征单根时 (A2t2+A t+Ao)eat 当ā是二阶特征根(二阶电路) cosβt 或 sin Bt A1cosβt+A2sinβt 当特解y(①)的函数形式确定后,将其代入原微分方程中,来求待定常数A 57页
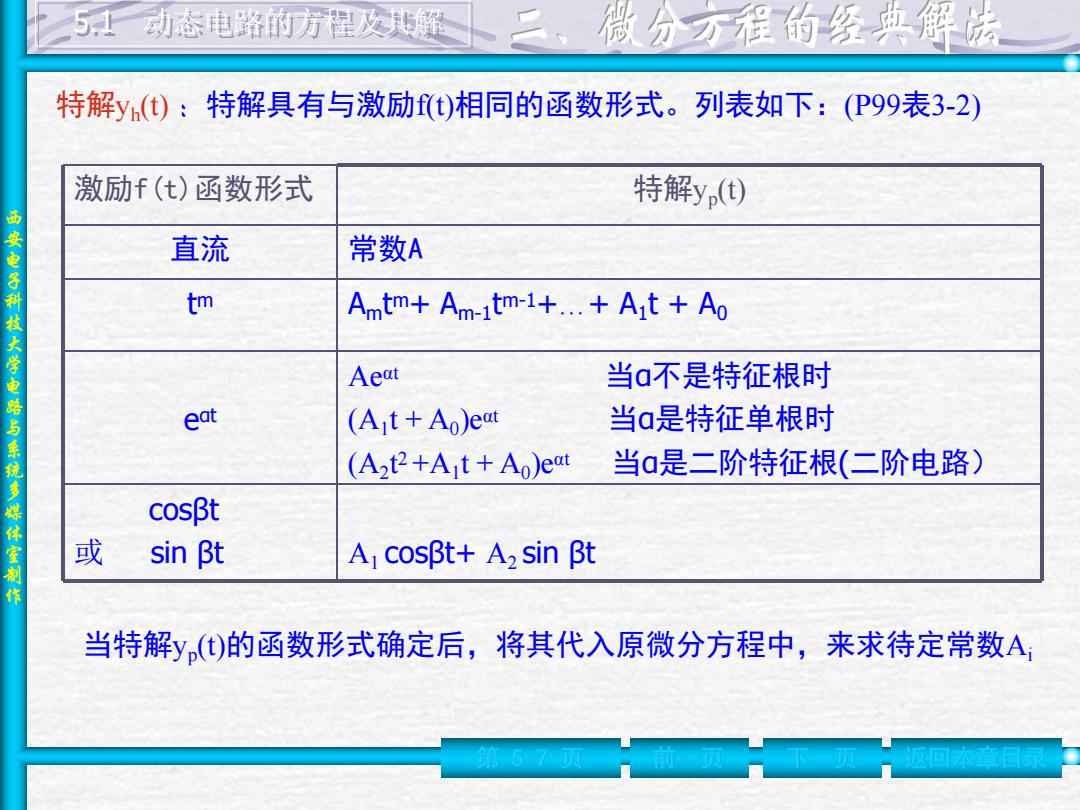
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 特解yh(t) :特解具有与激励f(t)相同的函数形式。列表如下:(P99表3-2) 第 5-7 页 前一页 下一页 返回本章目录 激励f(t)函数形式 特解yp(t) 直流 常数A tm Amtm+ Am-1 tm-1+…+ A1 t + A0 eαt Ae αt 当α不是特征根时 (A1 t + A0)e αt 当α是特征单根时 (A2 t2 +A1 t + A0)e αt 当α是二阶特征根(二阶电路) cosβt 或 sin βt A1 cosβt+ A2 sin βt 当特解yp(t)的函数形式确定后,将其代入原微分方程中,来求待定常数Ai 5.1 动态电路的方程及其解
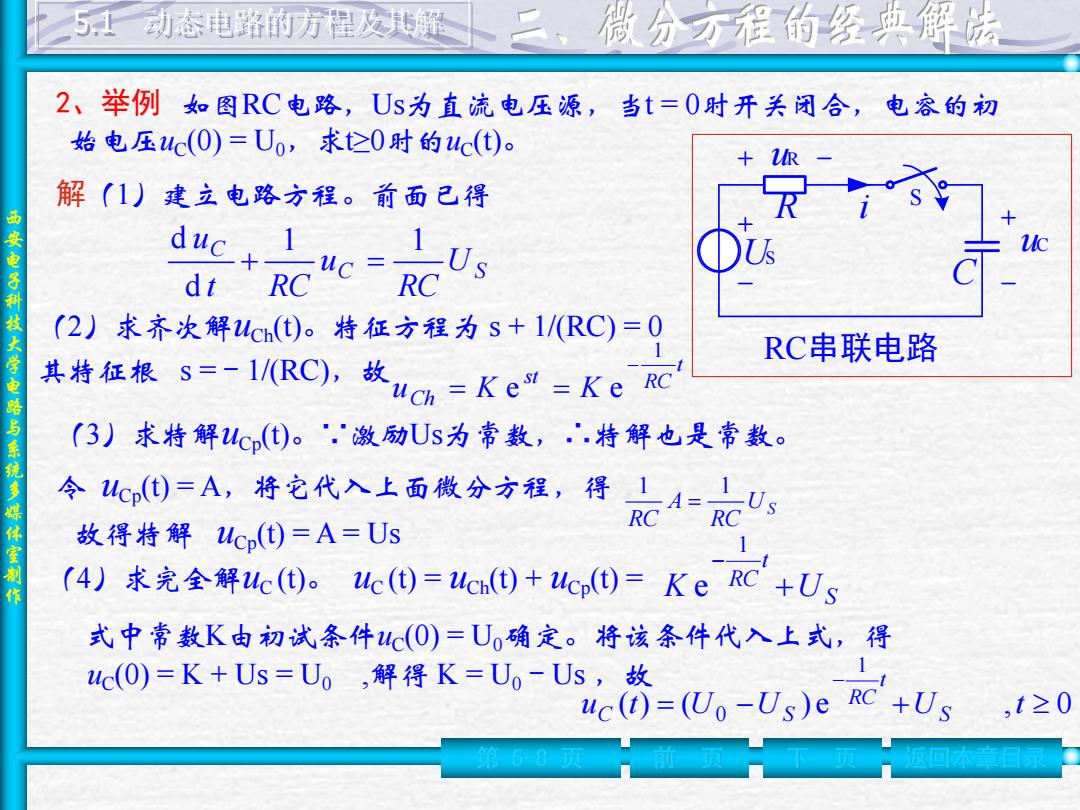
5上动态电路的方程及共骚 微分方程的经典解陆 2、举例 如图RC电路,Us为直流电压源,当t=0时开关闭合,电容的初 始电压uc(0)=Uo,求仑0时的lc(t)。 解(1)建立电路方程。前面己得 安电子 dt e-eUs RC RC (2)求齐次解uC()。特征方程为s+1/RC)=0 RC串联电路 电 共特征根s=-1(RC),故uC=Ke=KeC 与 (3)求特解山c(①)。,激励Us为常数,.,特解也是常数。 系统多 令0二A,将它代入上西微分方程,得底4忘 体 故得特解lcp()=A=Us 作 (4)求完全解uc(①)。ue(①)=uGn()+ucp(①)=KeRC+US 式中常数K由初试条件(0)=U0确定。将该条件代入上式,得 uc(0)=K+Us=U,解得K=Uo-Us,故 uc(t)=(Uo-Us)e RC +Us ,120 有58项
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 2、举例 第 5-8 页 前一页 下一页 返回本章目录 如图RC电路,Us为直流电压源,当t = 0时开关闭合,电容的初 始电压uC(0) = U0,求t≥0时的uC(t)。 S US uR uC R C i RC串联电路 解(1)建立电路方程。前面已得 C S C U RC u t RC u 1 1 d d (2)求齐次解uCh(t)。特征方程为 s + 1/(RC) = 0 其特征根 s = - 1/(RC),故 t st RC uCh K K 1 e e (3)求特解uCp(t)。∵激励Us为常数,∴特解也是常数。 令 uCp(t) = A,将它代入上面微分方程,得 U S RC A RC 1 1 故得特解 uCp(t) = A = Us (4)求完全解uC (t)。 uC (t) = uCh(t) + uCp(t) = S t K RC U 1 e 式中常数K由初试条件uC(0) = U0确定。将该条件代入上式,得 uC(0) = K + Us = U0 ,解得 K = U0 - Us ,故 ( ) ( ) e , 0 1 0 u t U U U t S t RC C S 5.1 动态电路的方程及其解

5上动态电路的方程及共解 微分方程的经典解法 3、结果分析:固有响应和强迫响应 暂态响应和稳态响应 uc(t)=(Uo-Us)e RC +Us ,t≥0 固有响应 强迫响应 西安电子科技大学电路与系统多媒体室制作 在完全解中,其第一项(即齐次解)的函数形式仅由特征根确定,而 与激动的函数形式无关,称为固有响应或自由响应。 式中第二项(即特解)与激励具有相同的函数形式,称为强迫响应。 按电路的工作情况,也常将完全响应分为暂态响应和稳态响应。上式 中第一项按指数规律衰减,→00时,该项为0,称为暂态响应。第二项在 任意时刻都保持稳定,称为稳态响应。 第59页 区回本章日际
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 3、结果分析:固有响应和强迫响应 暂态响应和稳态响应 第 5-9 页 前一页 下一页 返回本章目录 ( ) ( ) e , 0 1 0 u t U U U t S t RC C S 在完全解中,其第一项(即齐次解)的函数形式仅由特征根确定,而 与激励的函数形式无关,称为固有响应或自由响应。 固有响应 式中第二项(即特解)与激励具有相同的函数形式,称为强迫响应。 强迫响应 按电路的工作情况,也常将完全响应分为暂态响应和稳态响应。上式 中第一项按指数规律衰减,t→∞时,该项为0,称为暂态响应。第二项在 任意时刻都保持稳定,称为稳态响应。 5.1 动态电路的方程及其解
5.2电路的初始值 前面可以看到,求解微分方程时,需要根据给定的初始条件确定解答中 的待定常数K。由于电路的响应是指电压和电流,故相应的初始条件为电压 或电流的初始值,即在t=to时刻的值(o)、i(t)。 安电 其中电容电压uc和电感电流i的初始值(o)、(to)由电路的初始储能 决定,称为独立初始值或初始状态。其余电压电流的初始值称为非独立初 始值,它们将由电路激励和初始状态来确定。 学 ·、独立初始值 电 1、换路定律 与 (1)、换路现象 *开关的闭或开动作; 系统多媒体室制作 *元件参数突变; 统称为“换路” *电源数值突变; 电路的初始时刻一般认为是换路时刻。设换路时刻为t=to,则 换路前瞬间为:t0-=lim(to-8) 换路后瞬间为:to+=lim(to+ε) 8→0 8-→0 E>0 E>0 我们解微分方程所需要的初始值实际上是指在t+时刻的值
西 安 电 子 科 技 大 学 电 路 与 系 统 多 媒 体 室 制 作 1、换路定律 第 5-10 页 前一页 下一页 返回本章目录 前面可以看到,求解微分方程时,需要根据给定的初始条件确定解答中 的待定常数K。由于电路的响应是指电压和电流,故相应的初始条件为电压 或电流的初始值,即在t = t0时刻的值u(t0)、i(t0)。 其中电容电压uC和电感电流iL的初始值uC(t0) 、 iL (t0)由电路的初始储能 决定,称为独立初始值或初始状态。其余电压电流的初始值称为非独立初 始值,它们将由电路激励和初始状态来确定。 (1)、换路现象 * 开关的闭或开动作; * 元件参数突变; * 电源数值突变; 统称为“换路” 电路的初始时刻一般认为是换路时刻。设换路时刻为t = t0,则 换路前瞬间为: ( ) 0 0 0 0 lim t t 换路后瞬间为: ( ) 0 0 0 0 lim t t 我们解微分方程所需要的初始值实际上是指在t0+时刻的值