
第八章常微分方程数值解
1 第八章 常微分方程数值解

微分方程数值解 ■在科学研究或工程领城中,有许多数学模型都是通过 微分方程来描述的,求解微分方程是非常重要的、关 键的问题 ■微分方程按自变量的个数可分为: ●常微分方程 ●偏微分方程 ■微分方程按定解条件可分为: ●初值问题 ●边值问题
微分方程数值解 在科学研究或工程领域中,有许多数学模型都是通过 微分方程来描述的,求解微分方程是非常重要的、关 键的问题 微分方程按自变量的个数可分为: ⚫ 常微分方程 ⚫ 偏微分方程 微分方程按定解条件可分为: ⚫ 初值问题 ⚫ 边值问题 2

微分方程数值解 ■研究微分方程解析解的学科:数学物理方程,但是绝 大部分的微分方程是没有解析解的 ·数值求解微分方程没有统一的算法,针对不同类型的 微分方程,需要设计特定的算法 ■ 目前,研究数值求解微分方程的方法是热门的课题, 正在迅速发展之中,常见的方法: ●有限差分法 ●有限元方法 ●有限体积法 ●边界元方法 ●谱方法 ● 3
微分方程数值解 研究微分方程解析解的学科:数学物理方程,但是绝 大部分的微分方程是没有解析解的 数值求解微分方程没有统一的算法,针对不同类型的 微分方程,需要设计特定的算法 目前,研究数值求解微分方程的方法是热门的课题, 正在迅速发展之中,常见的方法: ⚫ 有限差分法 ⚫ 有限元方法 ⚫ 有限体积法 ⚫ 边界元方法 ⚫ 谱方法 ⚫ … 3

微分方程数值解 1958 ■常微分方程的初值问题: =f(x.),xela dx y(a)=yo ·为了使解存在雅一,一般需要对函数f(x,y)加限制条 件 ■(初值问题解的存在唯一性)若函数f(x,y)在条带 a≤x≤b,-oo<y<oo上连续,且满足Lipschitz条件, 即f(x,)-f(x,2≤L以-y2,则初值问题的解在区间 [a,b]上存在且雅一
微分方程数值解 常微分方程的初值问题: 为了使解存在唯一,一般需要对函数 加限制条 件 (初值问题解的存在唯一性)若函数 在条带 上连续,且满足Lipschitz条件, 即 ,则初值问题的解在区间 上存在且唯一 4 = = 0 ( ) ( , ) , [ , ] y a y f x y x a b dx dy f x y ( , ) 1 2 1 2 f x y f x y L y y ( , ) ( , ) − − f x y ( , ) a x b y − , [ , ] a b

微分方程数值解 ■ 常微分方程的解是一个函数,但是,计算机没有办法 直接对函数进行运算 ■常微分方程的数值解采用数值离散的方法,即在一系 列离散点列上,求未知函数在这些点上函数值的近似 ■基本步骤如下: (1)对区间进行分割:△,:a=x。<x1<…<xm=b(即对 函数定义城进行离散),目标是求解{y,=y(x)}的值 (2)对微分方程进行离散,建立关于{y}的方程,一 般要求满足:解的存在雅一性、稳定性、收敛性、相 容性 (3)解关于{y}方程,求出{y}的值 5
微分方程数值解 常微分方程的解是一个函数,但是,计算机没有办法 直接对函数进行运算 常微分方程的数值解采用数值离散的方法,即在一系 列离散点列上,求未知函数在这些点上函数值的近似 基本步骤如下: (1)对区间进行分割: (即对 函数定义域进行离散),目标是求解 的值 (2)对微分方程进行离散,建立关于 的方程,一 般要求满足:解的存在唯一性、稳定性、收敛性、相 容性 (3)解关于 方程,求出 的值 5 I : a = x0 x1 xm = b { ( )} i i y y x = { }i y { }i { } yi y

微分方程数值解 ■主要问题: ●如何对定义域进行离散? ●如何对微分方程进行离散? ●收敛性问题,即步长充分小时,所得到的数值解能否逼近问题的真解 ●误差估计 ·稳定性问题,即舍入误差在以后各步的计算中,是否会无限制扩大 ●计算效率 ·并行计算 6
微分方程数值解 主要问题: ⚫ 如何对定义域进行离散? ⚫ 如何对微分方程进行离散? ⚫ 收敛性问题,即步长充分小时,所得到的数值解能否逼近问题的真解 ⚫ 误差估计 ⚫ 稳定性问题,即舍入误差在以后各步的计算中,是否会无限制扩大 ⚫ 计算效率 ⚫ 并行计算 ⚫ …… 6
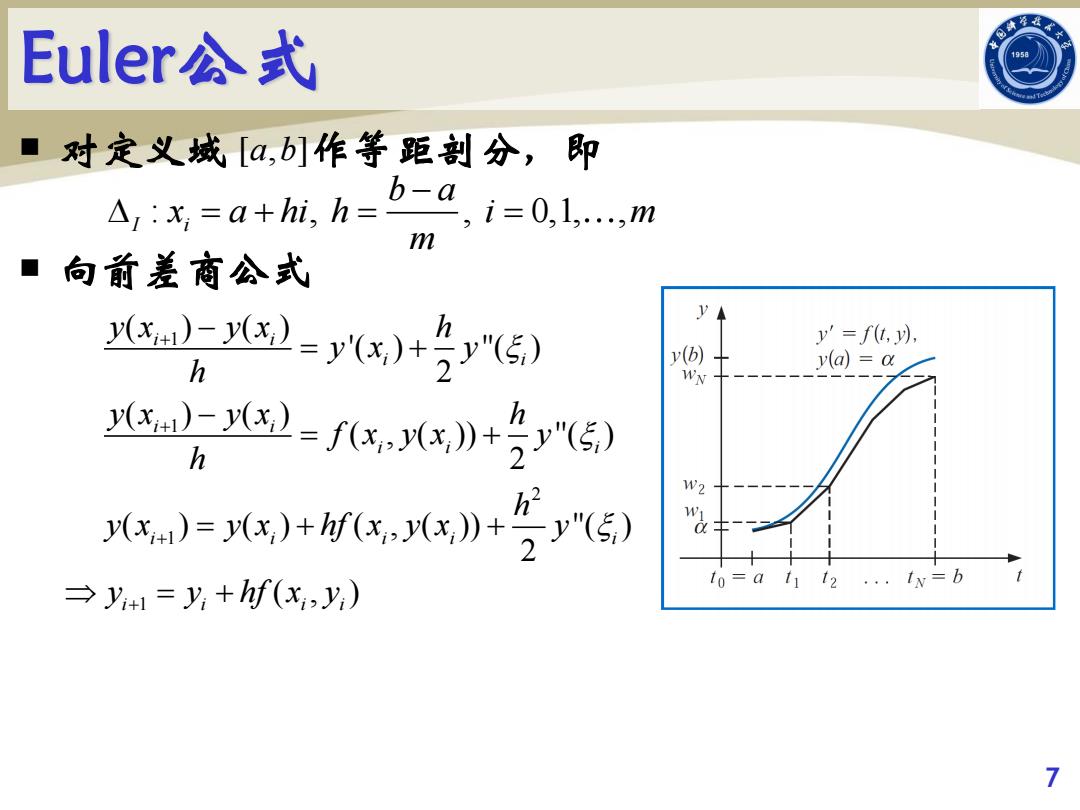
Euler公式 ■ 对定义域[a,b]作等距剖分,即 :a h=5-a.1=0.1..m m ■向前差商公式 -x)=y'(x)+3y"5) h y'=fu,以 y(b) h y(a)=a WN x)-=fx,x》+2"5) )=+》+行) W2 →y+1=y+hf(x,y,) =a ,,1x=b 7
Euler公式 对定义域 作等距剖分,即 向前差商公式 7 [ , ] a b : , , 0,1, , I i b a x a hi h i m m − = + = = 1 1 2 1 1 ( ) ( ) '( ) ''( ) 2 ( ) ( ) ( , ( )) ''( ) 2 ( ) ( ) ( , ( )) ''( ) 2 ( , ) i i i i i i i i i i i i i i i i i i y x y x h y x y h y x y x h f x y x y h h y x y x hf x y x y y y hf x y + + + + − = + − = + = + + = +

Euler公式 定义:在假设第步计算是精确的前提下,考虑载断误 差T1=y(x)-y1,称T+1为局部载断误差。若T=O(hP) ,则称方法是卫阶相容的,简称相容 ■向前差商公式的局部载断误差: T+1=y(x+1)-y+ h2 =x)+f(,x》+2"5)- h2 =x)+f(x(x》+2y"5)--f(x》 h2 =2) =0(h2) 8
Euler公式 定义:在假设第 步计算是精确的前提下,考虑截断误 差 ,称 为局部截断误差。若 ,则称方法是 阶相容的,简称相容 向前差商公式的局部截断误差: 8 i 1 1 1 ( ) T y x y i i i + + + = − Ti+1 1 1 1 2 1 2 2 2 ( ) ( ) ( , ( )) ''( ) 2 ( ) ( , ( )) ''( ) ( , )) 2 ''( ) 2 ( ) i i i i i i i i i i i i i i i i T y x y h y x hf x y x y y h y x hf x y x y y hf x y h y O h + + + + = − = + + − = + + − − = = 1 1 ( ) p T O h i + + = p

Euler公式 整体载断误差和收敛性:考虑局部载断误差的积果和 传播 e=y(x)- y(x)+hGx》+2")-片-(x,y ≤y(x,)-y+hf(x,y(x)》-f(x,y+T ≤le,+hLy(x)-y+|Tl s(1+hL)e,+T,T=max T, ≤(1+hL)(1+hL)e+T)+T =(1+hL)2le,+(1+hL)+1)T ≤(1+hL)2(1+hL)le,-2+T)+(1+hL)+1)7 =(1+hL)3le-2+(1+hL)2+(1+hL)+17 9
Euler公式 整体截断误差和收敛性:考虑局部截断误差的积累和 传播 9 ( ) 1 1 1 2 1 1 1 ( ) | ( ) ( , ( )) ''( ) ( , )) | 2 ( ) ( , ( )) ( , ) ( ) (1 ) , max (1 ) (1 ) (1 i i i i i i i i i i i i i i i i i i i i i i j j i e y x y h y x hf x y x y y hf x y y x y h f x y x f x y T e hL y x y T hL e T T T hL hL e T T + + + + + − = − = + + − − − + − + + − + + + = + + + + = + ( ) ( ) ( ) ( ) 2 1 2 2 3 2 2 ) (1 ) 1 (1 ) (1 ) (1 ) 1 (1 ) (1 ) (1 ) 1 i i i hL e hL T hL hL e T hL T hL e hL hL T − − − + + + + + + + + + = + + + + + +

Euler.公式 ■整体截断误差和收敛性: ≤… ≤(1+hL)e+(1+hL)'+…+(1+hL)+1)T =+y"e小+二+7 1-(1+hL) ≤1+hg,++h"7 hL ≤+"(+a) 是1阶方法 sew{+)}set(a*冠) 当a=00对,7=o)→e[+)>0,即Euler公式 是收敛的 10
Euler公式 整体截断误差和收敛性: 当 时, ,即Euler公式 是收敛的 10 ( ) 1 0 1 1 0 1 1 0 1 0 ( 1) ( ) 0 0 (1 ) (1 ) (1 ) 1 1 (1 ) (1 ) 1 (1 ) (1 ) (1 ) (1 ) i i i i i i i i hL b a L hL e hL hL T hL hL e T hL hL hL e T hL T hL e hL T T e e e e hL hL + + + + + + + − + + + + + + + − + = + + − + + + + + + + + 0 e h = → 0, 0 2 ( ) 0 ( ) 0 b a L T T O h e e hL − = + → 是1阶方法