
第一章插值 1
1 第一章 插值

插值问题 ■ 定义:f(x)为定义在区间[a,b]上的函数,xo,x,,xn为[a,b] 上+1个互不相同的点,Φ为给定的某一函数类。若Φ 上有函数o(x)满足: p(x)=f(x),i=0,1,…,n 则称p(x)为f(x)关于节点x,X,,Xn的插值函数 ■氵 称X0,X1,Xn为插值节点 ■称(x,f(x)为插值型值点 ■称f(x)为被插函数
¡ 定义: 为定义在区间 上的函数, 为 上 个互不相同的点, 为给定的某一函数类。若 上有函数 满足: 则称 为 关于节点 的插值函数 ¡ 称 为插值节点 ¡ 称 为插值型值点 ¡ 称 为被插函数 2 f (x) [a,b] 0 1 , , , n x x x [a,b] n 1 (x) ( ) ( ), 0,1, , i i x f x i n (x) f (x) 0 1 , , , n x x x 0 1 , , , n x x x ( , ( )) i i x f x f (x)
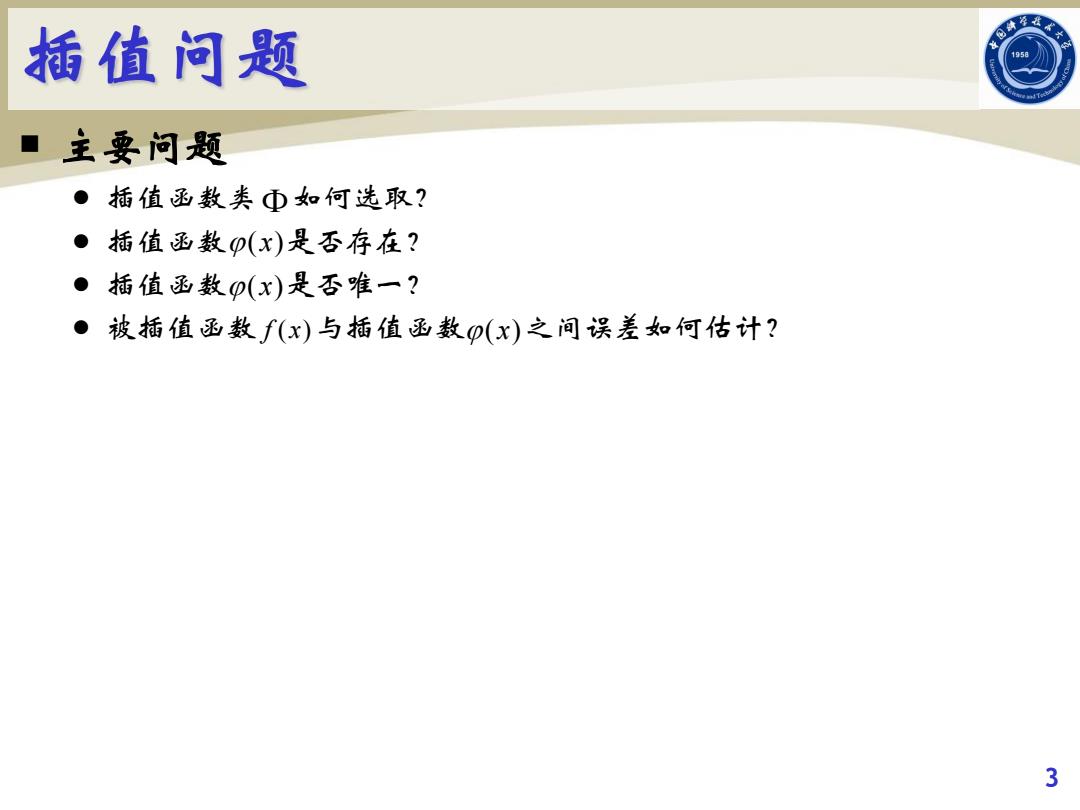
插值问题 ■主要问题 ●插值函数类①如何选取? ●插值函数p(x)是否存在? ·插值函数0(x)是否唯一? ●被插值函数f(x)与插值函数p(x)之间误差如何估计? 3
¡ 主要问题 l 插值函数类 如何选取? l 插值函数 是否存在? l 插值函数 是否唯一? l 被插值函数 与插值函数 之间误差如何估计? 3 (x) (x) f (x) (x)

插值问题 ■设p(x)=ap(x)+a,,(x)+…+ampm(x),则 f(x)=p(x)=ap(x,)+a10,(x,)+…+ampm(x),i=0,1,…,n ■n+1个方程,m+1个未知量的线性方程组 ■ 当且仅当m=n,det(A)≠0,方程组解存在且难一 4
¡ 设 ,则 ¡ 个方程, 个未知量的线性方程组 ¡ 当且仅当 , ,方程组解存在且唯一 4 0 0 1 1 ( ) ( ) ( ) ( ) m m x a x a x a x 0 0 1 1 ( ) ( ) ( ) ( ) ( ), 0,1, , i i i i m m i f x x a x a x a x i n n 1 m 1 m n det(A) 0

插值问题 ■(存在雅一性定理)设{x。为+1个互不相等的节点 ,Φ=Span{p,p1,,pn}为n+1维线性空间,则插值函数 (x)存在难一,当且仅当 1p(x)p,(xo)… 0n(xo) p(x)0,(x) …pn(x)) ≠0 o(x) 9(xn)… pn(xn) 5
¡ (存在唯一性定理)设 为 个互不相等的节点 , 为 维线性空间,则插值函数 存在唯一,当且仅当 5 0 n i i x n 1 0 1 span{ , , , } n n 1 (x) 0 0 1 0 0 0 1 1 1 1 0 1 ( ) ( ) ( ) ( ) ( ) ( ) 0 ( ) ( ) ( ) n n n n n n x x x x x x x x x
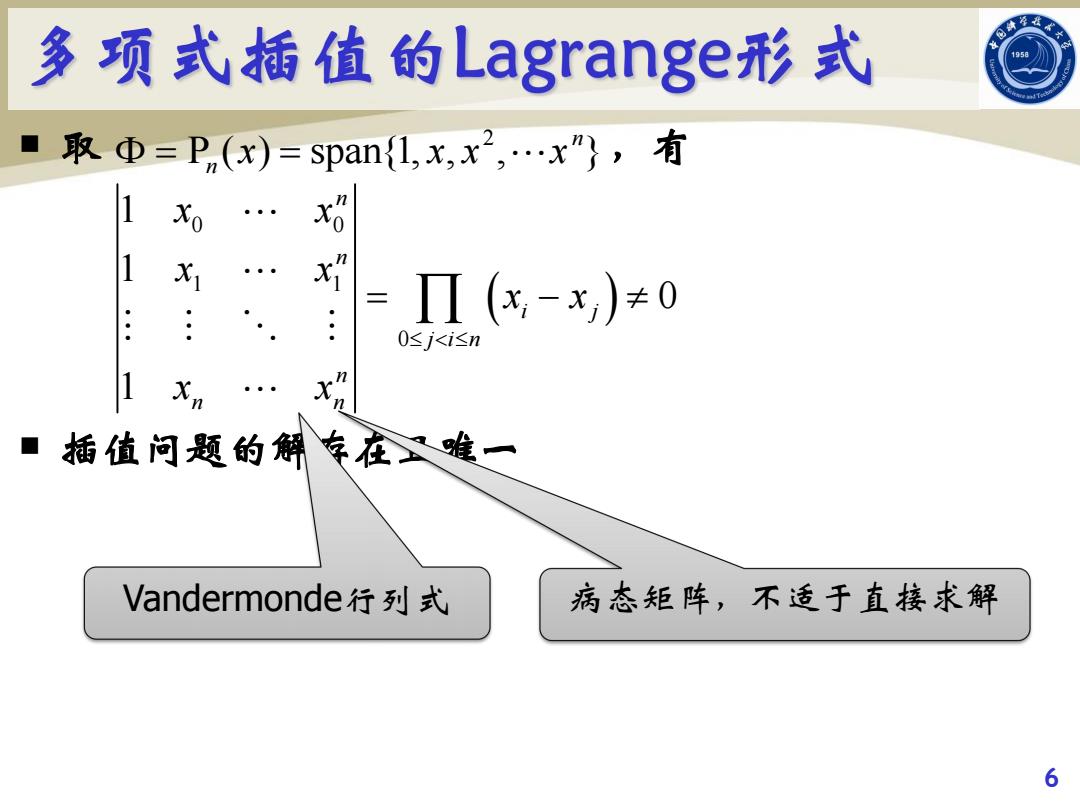
多项式插值的Lagrange形式 1958 取Φ=Pn(x)=pan{L,x,x2,…x"},有 Xo x =Π(x-x)≠0 0≤j<isn n ■ 插值问题的解车在义难一 Vandermonde行列式 病态矩阵,不适于直接求解 6
¡ 取 ,有 ¡ 插值问题的解存在且唯一 6 2 P ( ) span{1, , , } n n x x x x 0 0 1 1 0 1 1 0 1 n n i j j i n n n n x x x x x x x x Vandermonde行列式 病态矩阵,不适于直接求解

多项式插值的Lagrange:形式 如何选取中=Pn(x)=span{L,x,x2,…x")的另一组基,使 得插值问题便于求解? ■Lagrange.基函数{(x)}ocPn(x)满足 ./u. 7
¡ 如何选取 的另一组基,使 得插值问题便于求解? ¡ Lagrange基函数 满足 7 2 P ( ) span{1, , , } n n x x x x 0 { ( )} ( ) n i i n l x x 1, ( ) , , 0,1, , 0, i j ij i j l x i j n i j
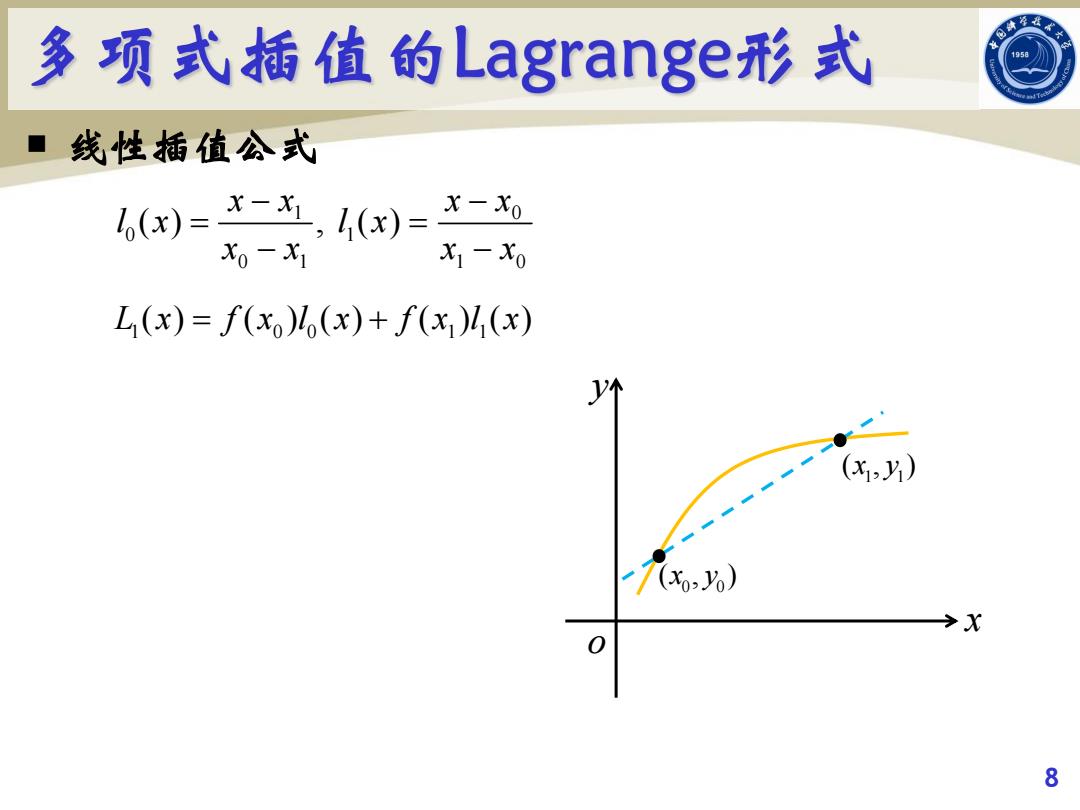
多项式插值的Lagrange形式 ■线性插值公式 ,(x)=X-,1()=- X0-x1 X1-X0 L(x)=f(xo)(x)+f(x)4 (x) >x 8
¡ 线性插值公式 8 o x y 0 0 (x , y ) 1 1 (x , y ) 1 0 0 1 0 1 1 0 ( ) , ( ) x x x x l x l x x x x x 1 0 0 1 1 L (x) f (x )l (x) f (x )l (x)

多项式插值的Lagrange:形式 1(误差估计)设L(x)为以(xo,f(x),(x,f(x)为插值点 的插值函数,xo,x,∈[a,b],x≠x1·设f(x)一阶连续可导 )f(x)在(a,b)上存在,则对任意给定的xe[a,b],重少 存在一点5x∈(a,b),使得 B)-FG)()).s(o.) 2! 9
¡ (误差估计)设 为以 为插值点 的插值函数, . 设 一阶连续可导 , 在 上存在,则对任意给定的 ,至少 存在一点 ,使得 9 1 L (x) 0 0 1 1 (x , f (x )), (x , f (x )) 0 1 0 1 x , x [a,b], x x f (x) '' f (x) (a,b) x [a,b] ( , ) x a b '' 1 1 0 1 ( ) ( ) ( ) ( ) ( )( ), ( , ) 2! x x f R x f x L x x x x x a b
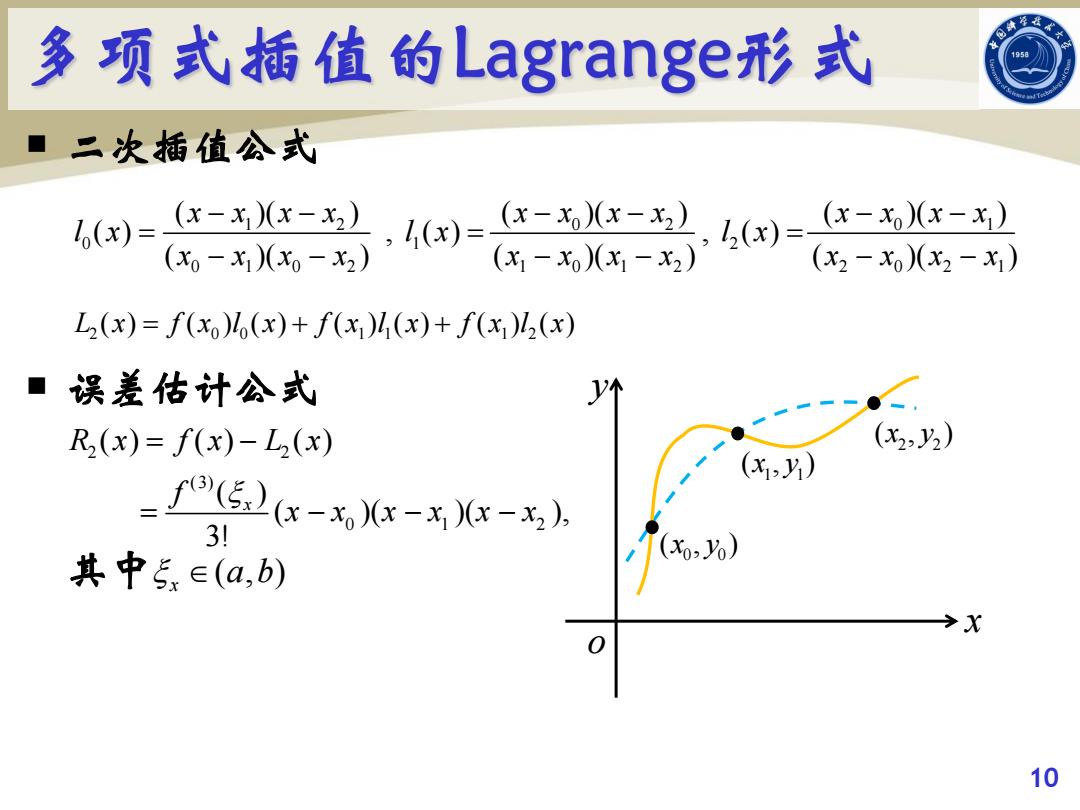
多项式插值的Lagrange形式 ·二次插值公式 田--巴-x-=-少 (x-x)(x-x2) (x1-)x1-x2) (x2-x)x2-x)) L2(x)=f(xo)(x)+f(x)(x)+f(x)2(x) ■误差估计公式 --● R(x)=f(x)-L2(x) (x2,2) (x,) -fP52(-xx-xXx-3,为 31 其中5∈(a,b) (x,%) >x 10
¡ 二次插值公式 ¡ 误差估计公式 其中 10 o x y 0 0 (x , y ) 1 1 (x , y ) 1 2 0 2 0 1 0 1 2 0 1 0 2 1 0 1 2 2 0 2 1 ( )( ) ( )( ) ( )( ) ( ) , ( ) , ( ) ( )( ) ( )( ) ( )( ) x x x x x x x x x x x x l x l x l x x x x x x x x x x x x x 2 0 0 1 1 1 2 L (x) f (x )l (x) f (x )l (x) f (x )l (x) 2 2 (x , y ) 2 2 (3) 0 1 2 ( ) ( ) ( ) ( ) ( )( )( ), 3! x R x f x L x f x x x x x x ( , ) x a b