
第三章数值微分和数值积分 1
1 第三章 数值微分和数值积分

数值微分 函数∫(x)未知或非常复杂的情形下,如何求导数? ■导数的通近:差商 f'(x)=lim f(x+h)-f(x) h→0 h lim f(x)-f(x-h) h-→0 h f(x+h)-f(x-h) =lim h->0 2h 载断误差 ■步长的选取 2
¡ 函数 未知或非常复杂的情形下,如何求导数? ¡ 导数的逼近:差商 ¡ 截断误差 ¡ 步长的选取 2 f (x) 0 0 0 ( ) ( ) '( ) lim ( ) ( ) lim ( ) ( ) lim 2 h h h f x h f x f x h f x f x h h f x h f x h h
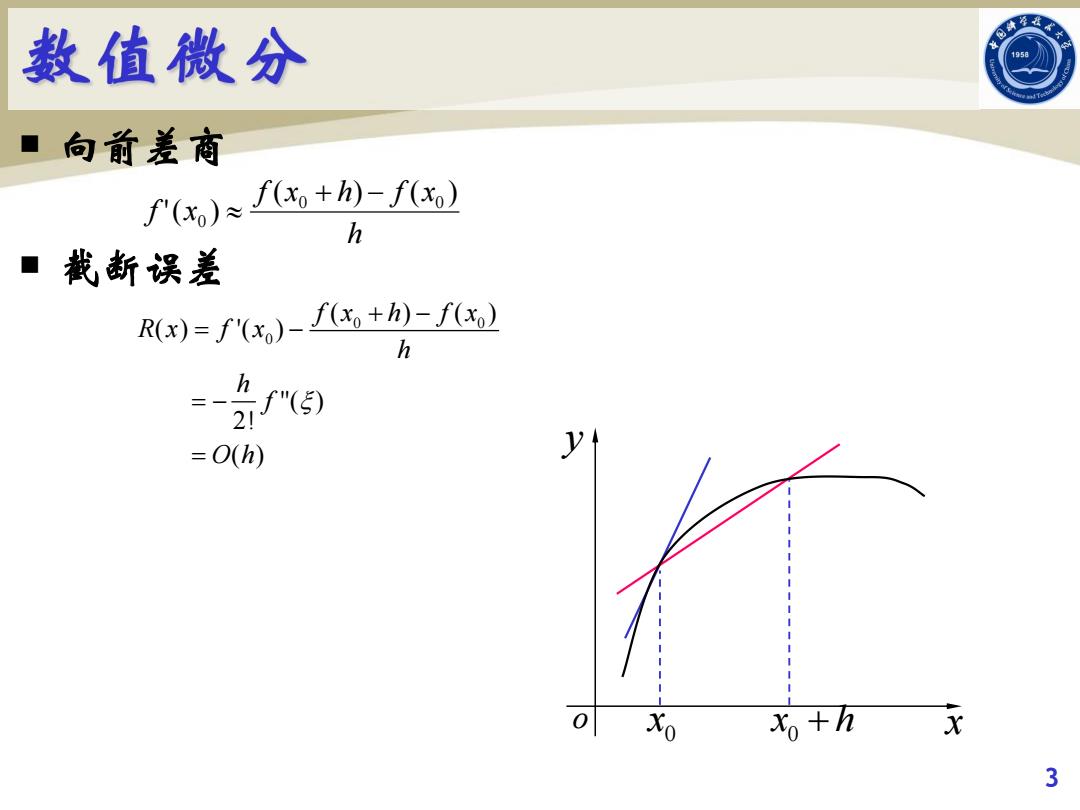
数值微分 ■ 句前差商 f(x)f+)-f) h 载断误差 R()=f(x,)-f+h-f) h =O(h) y 0 Xo X 3
¡ 向前差商 ¡ 截断误差 3 h f x h f x f x ( ) ( ) '( ) 0 0 0 o x y 0 x 0 x h 0 0 0 ( ) ( ) ( ) '( ) ''( ) 2! ( ) f x h f x R x f x h h f O h
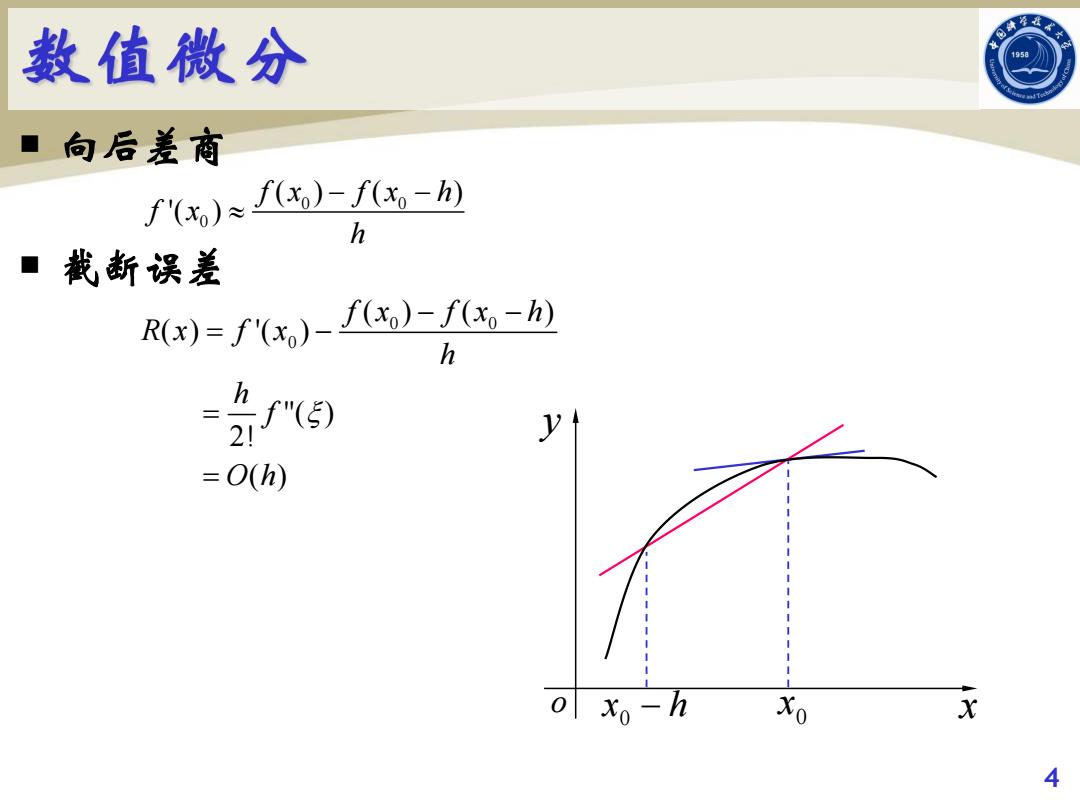
数值微分 ■ 向后差商 f'(x))-f-) h 载断误差 R(x)=f'(x)- f(xo)-f(xo-h) h h f"(5) y =O(h) o xo-h Xo 4
¡ 向后差商 ¡ 截断误差 4 0 0 0 ( ) ( ) '( ) f x f x h f x h 0 0 0 ( ) ( ) ( ) '( ) ''( ) 2! ( ) f x f x h R x f x h h f O h o x y 0 x h 0 x
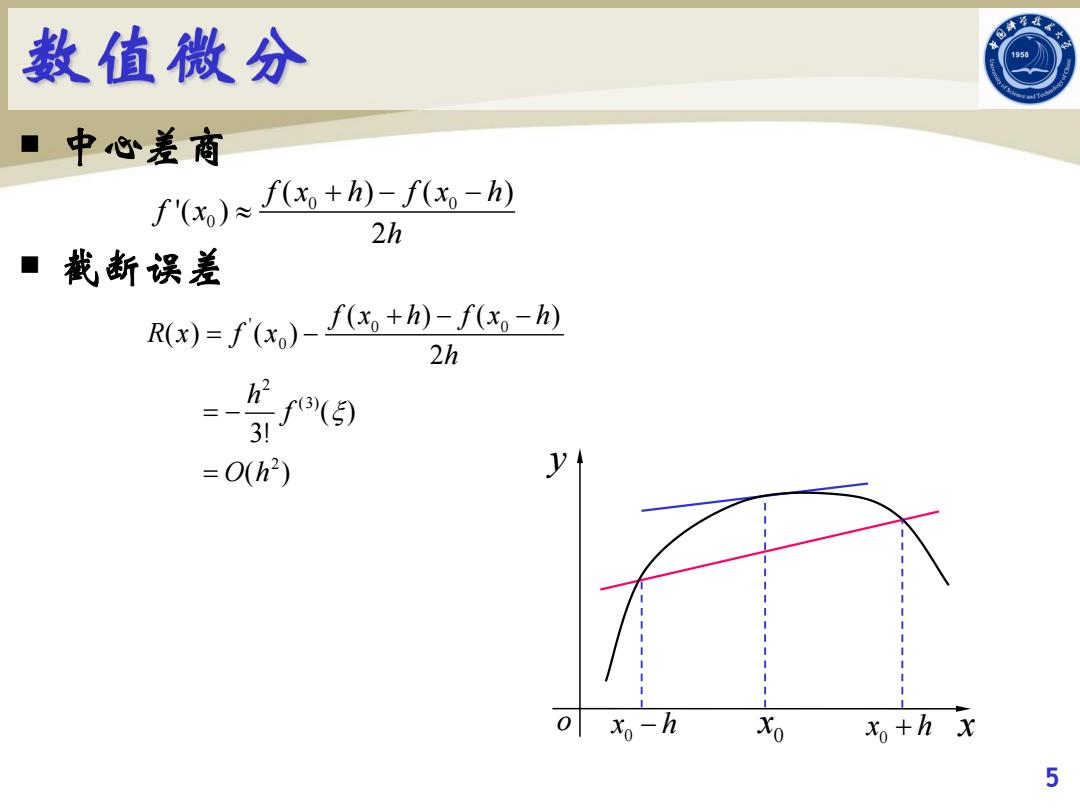
数值微分 中心差商 f(x,)fx+)-f,-) 2h 载断误差 R(x)=f(xo)- f(x,+h)-f(x。-h) 2h f8(9 31 =0h2) y o xo-h Xo xo+h x 5
¡ 中心差商 ¡ 截断误差 5 0 0 0 ( ) ( ) '( ) 2 f x h f x h f x h ' 0 0 0 2 (3) 2 ( ) ( ) ( ) ( ) 2 ( ) 3! ( ) f x h f x h R x f x h h f O h o x y 0 x h 0 x 0 x h

数值微分 m ■如何设定步长? ■ 理论估计 :数套:186→h-暖 ●舍入误差:e/h ■事后估计 ·设Dh,x),D(h/2,x)分别是取步长h,h/2的差商计算公式f(x),对于给定的 误差界£,则当 D(h,x)-D(h/2,x)<8 时,步长h就是合适的步长h 6
¡ 如何设定步长? ¡ 理论估计 l 截断误差: l 舍入误差: ¡ 事后估计 l 设 分别是取步长 的差商计算公式 ,对于给定的 误差界 ,则当 时,步长 就是合适的步长 6 2 (3) 2 m 3 h ax | f (x) | /6 h M / 6 e / h 3 3 3e h M D(h, x),D(h / 2, x) h,h / 2 ' f (x) D(h, x) D(h / 2, x) h h

数值微分 ■插值型数值微分 ●对于给定f(x)的函数表,建立插值函数L(x),用插值函数L(x)的导数近 似函数f(x)的导数 fx)≈L,(x)=∑fx,),(x) i=0 f(x)≈L,(x)=∑f(x)M(x) x=xf(x)L()=>f(x4() ●误差估计公式 w-小 )=aEΠx,- (n+1)!os+n 7
¡ 插值型数值微分 l 对于给定 的函数表,建立插值函数 ,用插值函数 的导数近 似函数 的导数 l 误差估计公式 7 f (x) L(x) L(x) f (x) 0 ' ' ' 0 ' ' ' 0 ( ) ( ) ( ) ( ), ( ) ( ) ( ) ( ), , ( ) ( ) ( ) ( ). n n i i i n n i i i n j j n j i i j i f x L x f x l x f x L x f x l x x x f x L x f x l x ( 1) 0 ( 1) 0 ( ) ( ) ( ) , ( 1)! ( ) ( ) ( ). ( 1)! n n i i n j j i i j n d f R x x x dx n f R x x x n

数值微分 ■ 数值微分的三点公式 ●给定{(x,f(x)}。,并有2-x=x-x=h,则 ()+)+f) 2h2 -h2 2h L,)=《=x+-f)+=+-》f)+任=t-f0 2h2 -h2 2h2 U )e)-)*4)-)小g )L)=x)+)g(3 ))2方)-4x)+3)好f为 ■类似可得数值微分的五点公式 ■用其它插值函数方法类似,如三次样条函数插值 8
¡ 数值微分的三点公式 l 给定 ,并有 ,则 ¡ 类似可得数值微分的五点公式 ¡ 用其它插值函数方法类似,如三次样条函数插值 8 2 0 ( , ( )) i i i x f x 2 1 1 0 x x x x h 1 2 0 2 0 1 2 2 0 2 1 2 2 ( )( ) ( )( ) ( )( ) ( ) ( ) ( ) ( ), 2 2 x x x x x x x x x x x x L x f x f x f x h h h 1 2 0 2 0 1 2 2 0 2 1 2 2 ( ) ( ) ( ) ' ( ) ( ) ( ) ( ), 2 2 x x x x x x x x x x x x L x f x f x f x h h h 2 0 2 0 0 1 2 2 1 2 1 0 2 2 2 2 2 0 1 2 1 '( ) ' ( ) 3 ( ) 4 ( ) ( ) '''( ), 2 3 1 '( ) ' ( ) ( ) ( ) '''( ), 2 6 1 '( ) ' ( ) ( ) 4 ( ) 3 ( ) '''( ) 2 3 h f x L x f x f x f x f h h f x L x f x f x f h h f x L x f x f x f x f h

数值积分 Newton-Leibniz.公式,Green.公式,Gauss公式, Stokes.公式 ■很多积分无解析解,必须使用数值方式求解 ·从积分的定义出发 1f)=fx)k=lim∑fs) △x>0 2afx)=1,f) i=( ●求积节点{x} ·求积系数{a,}
¡ Newton-Leibniz公式,Green公式,Gauss公式, Stokes公式 ¡ 很多积分无解析解,必须使用数值方式求解 ¡ 从积分的定义出发 l 求积节点 l 求积系数 9 0 0 0 ( ) ( ) lim ( ) ( ) ( ) i n b i i a i x n i i n i I f f x dx f x x f x I f { } i { }i x

数值积分 1958 ■代数精度:衡量数值积分公式优劣的重要指标之一 ●设[a,b]上以x,i=0,l,,n为积分节点的数值积分公式为 I.(-af) 若Ln(f)满足 In(x)=I(x),i=0,…,kg In(x+)≠I(x+), 则称I,(f)具有k阶代数精度 ■ 性质:当I(f)具有k阶代数精度时,对任意不高于k 次的多项式p(x),有In(p)=I(p) 10
¡ 代数精度:衡量数值积分公式优劣的重要指标之一 l 设 上以 为积分节点的数值积分公式为 若 满足 则称 具有 阶代数精度 ¡ 性质:当 具有 阶代数精度时,对任意不高于 次的多项式 ,有 10 [a,b] , 0,1, , i x i n 0 ( ) ( ), n n i i i I f f x ( ) n I f 1 1 ( ) ( ), 0, , ; ( ) ( ), i i n k k n I x I x i k I x I x ( ) n I f k ( ) n I f k k p(x) ( ) ( ) n I p I p