
负荷模型 一、负荷特性 ●负荷特性:负荷功率和节点电压及频率的 关系,即P,Q和U,f的关系。 。电压和频率的变化直接影响该节点上的负 荷的工况,即负荷从网络吸收的功率。 ●负荷变化又反过来影响系统的电压和频率
负荷模型 一、负荷特性 负荷特性:负荷功率和节点电压及频率的 关系,即PL ,QL和U,f 的关系。 电压和频率的变化直接影响该节点上的负 荷的工况,即负荷从网络吸收的功率。 负荷变化又反过来影响系统的电压和频率

当系统发生扰动时,U,f发生变化,引起负荷P,O的变化; 而P,Q,的变化又反过来影响U,f,这种相互作用,使得分析 稳定问题更为复杂。 因此要研究系统的稳定性,必须了解负荷特性。 负荷分布广,数量大,种类多,使得在稳定研究中负荷模型的 准确选用十分困难,是目前电力系统研究中的主要难点之一

在一般的稳定研究中,描述负荷特性的方法主要有以下三种: 恒定阻抗负荷模型。方法简单,但误差较大, 只适用于近似计算分析。 异步电动机模型。可以描述在扰动过程中负荷的动态行为, 适合于各种稳定分析,但参数的获取十分困难,一般只能采用典型参数。 综合负荷的静态模型。 采用一组代数方程描述负荷吸收的功率与节点电压及频率的关系, 参数按运行经验或试验识别得到。 下面分别详细讲述三类负荷模型的表示方法

二、恒定阻抗模型 假设所有负荷均为恒定阻抗(或恒定导纳)。 这样做,实际上就是近似地认为负荷从系统吸收的功率 总是正比于负荷节点电压的平方。 Z=R+ix,P.=U2 g2=0年g R 这是最简单的处理负荷的方法
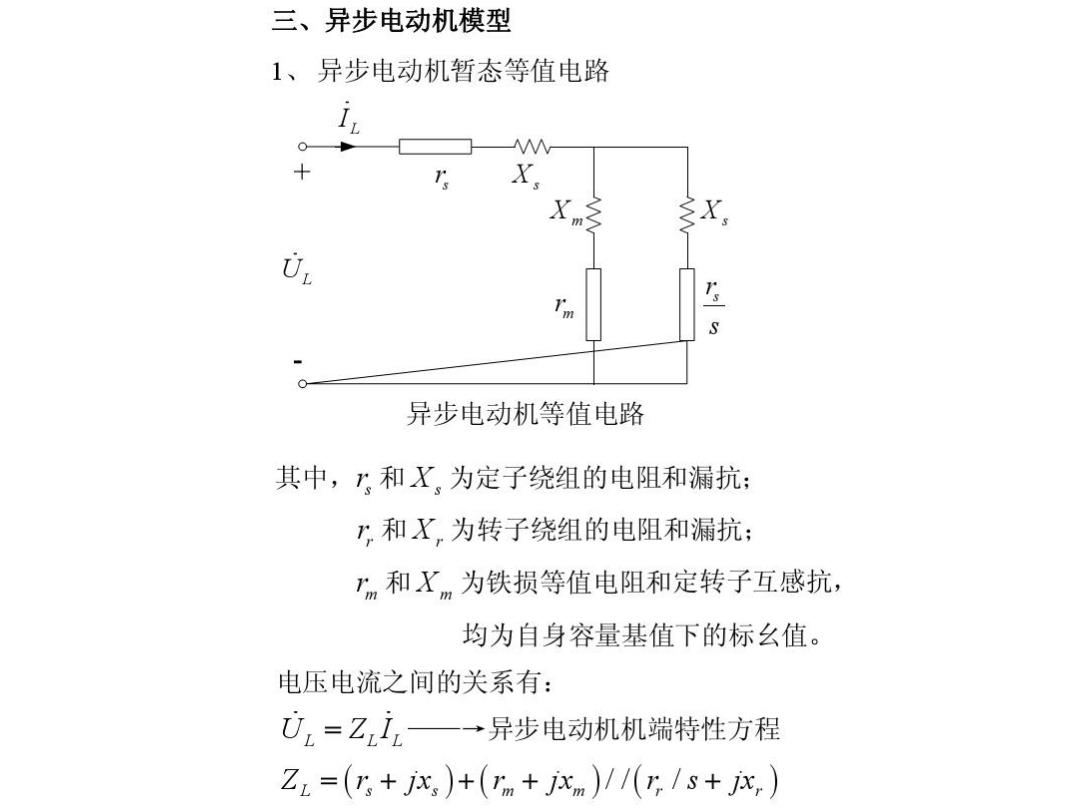
三、异步电动机模型 1、异步电动机暂态等值电路 + X. x, 异步电动机等值电路 其中,和X、为定子绕组的电阻和漏抗: )和X,为转子绕组的电阻和漏抗: ”m和Xm为铁损等值电阻和定转子互感抗, 均为自身容量基值下的标么值。 电压电流之间的关系有: U,=Z,,—→异步电动机机端特性方程 ZL=(,+jx,)+(m+jxm)1/(r,/s+jx,)

2、异步电动机组转子运动方程 d @=Mg-MM T, 式中:T,异步电动机惯性时间常数,一般约为2s。 M从系统中吸收的电磁转矩, My异步电动机拖动的机械负载的转矩 除t和T,外,均为标么值

do=Mg-MM 工dt 定义异步电动机的转差率S= 0一0有名=1一0 Wo (也称为电动机滑差),因此可以得到关系式 dk_d1-o)- dt dt d@,代入转子运动方程, dt 可以得到转差率和不平衡转矩之间的关系: ds =MM-Mg 工 一→描述异步电动机机械特性的转子运动方程 那么MM和ME如何计算呢?
*

a)机械负载的转矩MM Mx=ka+(-a)1-s) 其中,飞称为负荷率,k=实际负荷/额定负荷, 由稳态时的Mo和s。待定而得: 《为异步电机静止阻力矩: B为机械负载中与转速有关的指数

b)电磁转矩ME ME- Uir 1 r+5/s)2+(x+x,)2S 式中:”为定子绕组电阻, 5为转子绕组电阻, x。和x,。分别对应定子和转子的对应的电抗参数。 因为滑差s通常很小,因此有r/s>”,忽略, 则电磁转矩可写为: U21- U22,s Mg=G,/y+民+x了s7+3c,+了

求电磁转矩M对滑差s的偏导数,并且令 aME=0。 0s aMgr2+s2(+r-(2s)Uirs0 0s [2+s2(c+x] →(;2+s2(x+x,)2)U-(2s(x,+x,)2)U2s=0 (推导:→02+92x,+x)水-(2(飞+x})5s=0,因此s,=) =2+s2(x,+x)2-2s2(x+x,)2=0 x。+x →2-82(x,+x,)2=0 就可以得到临界滑差8。,也就是转矩最大时对应的滑差:3= X。+x 可以看出临界滑差只与异步电机的参数有关,而与运行方式和运行状况无关