
目录 1绪论-最优控制发展简史 先进控制技术 第一节绪论 能提系终视装的被法:高酒受来能心思是如选邦机制 第二节数学准备 一:最优控制的发展 第二次世界大战以后发展起来的自动调节原理。对设计与分析单输入单 输出的线炸定常系统是有的:然而近代航空及空间技术的发展对控制 最优控制 第三节用变分法求解最优控制问题 精度提出了领高的数球,并目城拉的对像是多转入多地出的,参数是 彭超 第四节极小值原理及其应用 城本无法定义,对多验入多输出系统从传送数板念得出的工程结论 第五节线性二次型问题的最优控制 住往造于应用。由于工程技不的需要,以状态空问探念力基础的最优拉 制建论新新发展起来,最优拉制理论是现代控制近论的核心, 20世纪50年代发展起来的,已形减系统的理论,最优掉制理论所要解决 第六节动态规划法 1绪论-研究最优整制的方法 1.绪论-研究最优控制的方法 1绪论-最优控制问题的实例 听究录代业制的方法 ,球上物球陆亚 从数学方面看,最优控制问避藏是求解一类带有钓束条件的泛函极值月题 求解最优控制问题,可以采用解析法或数值计算法 因此这是一个变分学的月四:然而变分理论只是解决容许控制属干开集的 一类数代制问,而在工程实中还常容控制属于集的一类取 由干电子计算机技术的发展,使得设计计算积实时控制有了实际可 夏飞船精景为灯 优控制问题,这碱要求人们研究新方法 用的计算工具,为际应用 些更完香的数学方法提供了工积实别 的物婚条件。高速度、大容量计草机的应用。一方商使物制理论的 嘴经 在研究最优控制的方法中,有两种方法最富成效:一种是苏联学者成特型 雅金提曲的“极大能原理”:另一种是美国学者贝尔曼提出的“动态规 工程实现有了可能,另一 0n0 M0-4 初始缘件 m (-F 吸大植原理是成特平雅金等人在19S6至 过心规是贝尔显在19钙年至 15甲间逐步创立的,他禁起最优 最优控制理论在一些大型的或复条的控制系筑设计中,已经取得了 锋璃条件,一0 物率条件三a0≤位 值进的站论,随后我设供了一种证明 有成效的实应用。 4,=0 方法 性能州晰是使世料滴耗为最小,爵了▣,》达到最大值 8 应满见约更条件,便飞船中们始 1
1 先进控制技术 最优控制 彭超 第一节 绪 论 第二节 数 学 准 备 第三节 用变分法求解最优控制问题 第四节 极小值原理及其应用 第五节 线性二次型问题的最优控制 第六节 动态规划法 目录 最优控制是系统设计的一种方法。它所研究的中心问题是如何选择控制 信号才能保证控制系统的性能在某种意义下最优。 一:最优控制的发展 第二次世界大战以后发展起来的自动调节原理,对设计与分析单输入单 输出的线性定常系统是有效的;然而近代航空及空间技术的发展对控制 精度提出了很高的耍求,并且被控制的对象是多输入多输出的,参数是 时变的。面临这些新的情况.建立在传递函数基础上的自动调节原理就 日益显出它的局限性来。这种局限性首先表现在对于时变系统,传递函 数根本无法定义,对多输入多输出系统从传递函数概念得出的工程结论 往往难于应用。由于工程技术的需要,以状态空间概念为基础的最优控 制理论渐渐发展起来。最优控制理论是现代控制理论的核心, 20世纪50年代发展起来的,已形成系统的理论。最优控制理论所要解决 的问题是:按照控制对象的动态特性,选择一个容许控制,使得被控对 象按照技术要求运转,同时使性能指标达到最优值。 1.绪论-最优控制发展简史 研究最优控制的方法 从数学方面看,最优控制问题就是求解一类带有约束条件的泛函极值问题, 因此这是一个变分学的问题:然而变分理论只是解决容许控制属于开集的 一类最优控制问题,而在工程实践中还常遇到容许控制属于闭集的一类最 优控制问题,这就要求人们研究新方法。 在研究最优控制的方法中,有两种方法最富成效:一种是苏联学者庞特里 雅金提出的“极大值原理”;另一种是美国学者贝尔曼提出的“动态规 划”。 极大值原理是庞特里雅金等人在1956至 1958年间逐步创立的,先是推测出极大 值原理的结论,随后又提供了一种证明 方法。 动态规划是贝尔曼在1953年至 1958年间逐步创立的,他依据最优 性原理发展了变分学中的哈密顿-雅 可比理论,构成了动态规划。 1.绪论-研究最优控制的方法 由于电子计算机技术的发展,使得设计计算和实时控制有了实际可 用的计算工具,为实际应用—些更完善的数学方法提供了工程实现 的物质条件,高速度、大容量计算机的应用,一方面使控制理论的 工程实现有了可能,另一方面又提出了许多需要解决的理论课题, 因此这门学科目前是正在发展的,极其活跃的科学领域之一。 最优控制理论在一些大型的或复杂的控制系统设计中, 已经取得了 富有成效的实际应用。 求解最优控制问题,可以采用解析法或数值计算法 1.绪论-研究最优控制的方法 例1.1月球上的软着陆问题 飞船靠其发动机产生一与月球重力方向相反的推力u(t),以使 飞船在月球表面实现软着陆,要寻求发动机推力的最优控制 规律,以便使燃料的消耗为最少。 设飞船质量为m(t),高度为h(t),垂直速度为v(t),发动机推 力为u(t),月球表面的重力加速度为常数g。设不带燃料的飞 船质量为M, 初始燃料的总质量为F.初始高度为h0 ,初始 的垂直速度为v0 ,那么飞船的运动方程式可以表示为: ( ) ( ) ( ) ( ) ( ) ( ) ( ) m t ku t m t u t v t g h t v t 初始条件 m M F v v h h (0) (0) (0) 0 0 终端条件 ( ) 0 ( ) 0 f f v t h t 性能指标是使燃料消耗为最小,即 约束条件 0 u(t) ( ) f J m t 达到最大值 我们的任务是寻求发动机推力的最优控制规律u(t),它应满足约束条件,使飞船由初始 状态转移到终端状态,并且使性能指标为极值(极大值)。 1.绪论-最优控制问题的实例

1绪论-最优控制问题的实例 1绪论-最优控制向题的实例 1绪论-最优控制闲题的提法 一兰业利 在某一横性坐标系内,授栏酸器质心的位置矢量和速废关量为:【红元 从工程安标考虑,。约来条桥为●金FU三nF) 在叙述最优控制月题的提法之藕,先讨论一些基本概之。 日标饭心的位置失量和速度矢绿为:x业玉y 如要我们慨要家栏戴过程的时何尿最短,又烫求燃料消耗尽绿少, 1:史接现的的徽糯通 得为栏藏器的孩力玉=工红一工wv=至2一无 则可取性能指标: 装我瓷雾翰受技系统绝可以用一帽一修备分方程来标达,事秋志方色 侧超截惠与日标的积时运动方程为知 J-6+恤为敏本 f(n-f(x(m) i=a0+0,扇=-f0 X-马,,”是n诚状态向量 一,,,广为p控制向 综上所速,所用最优病天指做间圆。即透满足约桌条桥的控树F间,影使系统 mt) 风初始状志出发的解。在某个时时满足路病条件。且使性能游标为酸值《程 xt,以)为n雄请量向量 其中0是学控制加速度外的州有积时加速度,是己知的 小幢)· 「f八I,时门「,…,a,…a,h (0ko(r) 初始条并为,》=马,。)-男,)一属 tu-f(xn.- 选演条件为:,-0形:意2气 u f5-马-, 1绪论-最优整制问题的提法 1绪论-最优控制门题的提法 1绪论-最优拉制间题的提法 2:月标麻 34零南控 51最我的业 多支是生产尔。在线金中,也志 己知受控系统的状志方程及给定的初志 两质鞋酸鞋林幸紫中的一个血。度事先保化的器肉。 0sd)s&l上a1-l2p to-fxin.uin.n x)-x0) 上送主控约索乐规定的黄称为控制城山。凡在4上有定文。目在控制U g,=0 内取的海一个控制数u均称力客控制 提定前日标集为幽,求一容许控制明EUE几从使系统从给定的初恋出发 在时钢转到日标M,使 g,4,)s0 透常情况下,顾优拉刺问圆的性候指标形如 请足末态构家的状态泰合称为日标集。记为M,即: J-0 (at,)+F (atnhu(nnd J-0 Gu,M+[F (athatthekdr 为最小, M=可k,)cR,8y,)=0,g(yh)s0g 其中第一项是按近日标集程度。即末老控刺精度的变量,称为衣植性能带标。 这微是最优拉制侧题。 哥富费布灵程经程是特智般地用阿志约电来来标 第二项为积分性能指标,它反映控刺过程偏差在某件意义下的平均或制 如果阿圆有解,记为u阳,E6品刚ú间叫做量优控制(极值控制),相应的敏 找X间蒂为最优轨线《酸值轨战),而隆能标〔心)则称为最优性能指与 过程的快速性,时楚反映世料成能量的诵耗。 2
2 例1—2拦截问题 在某一惯性坐标系内,设拦截器质心的位置矢量和速度矢量为: L x L x 目标质心的位置矢量和速度矢量为: F(t)为拦截器的推力 M x M x x xL xM v xL xM 则拦截器与目标的相对运动方程为: c F t m m t F t v a t x v ( ) ( ) ( ) ( ) , 其中a(t)是除控制加速度外的固有相对加速度,是已知的。 初始条件为: 0 0 0 0 0 0 x(t ) x v(t ) v m(t ) m 终端条件为: x(t f ) 0 v(t f )任意 f me m(t ) 1.绪论-最优控制问题的实例 从工程实际考虑,约束条件为 0 F(t) maxF(t) 如果我们既要求拦截过程的时间尽量短,又要求燃料消耗尽量少, 则可取性能指标: f t t J c F t dt 0 [ ( )] 1 为最小 综上所述,所谓最优防天拦截问题,即选择满足约束条件的控制F(t),驱使系统 从初始状态出发的解,在某个时刻满足终端条件,且使性能指标为极值(极 小值)。 1.绪论-最优控制问题的实例 在叙述最优控制问题的提法之前,先讨论一些基本概念。 1:受控系统的数学模型 一个集中参数的受控系统总可以用一组一阶微分方程来描述,即状态方程, 其一般形式为: X (t) f (X (t),u(t),t) T n X [x , x , , x ] 1 2 是n维状态向量 T u u u up [ , , , ] 1 2 为p维控制向量 f (X (t),u(t),t) 为n维函数向量 ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ) ( ), ( ), ( ) ( ), ) ( ( ), ( ), ) ( ( ), ( ), ) ( ( ), ( ), ) ( ) ( ( ), ( ), ) 1 2 1 2 2 1 2 1 2 1 1 2 1 2 2 1 f x t x t x t u t u t u t t f x t x t x t u t u t u t t f x t x t x t u t u t u t t f X t u t t f X t u t t f X t u t t X t f X t u t t n n p n p n p n 1.绪论-最优控制问题的提法 2:目标集 如果把状态视为n维欧氏空间中的一个点,在最优控制问题中,起始状态(初 态)通常是已知的,即 ( ) (0) X t0 X 而所达到的状态(末态)可以是状态空间中的一个点,或事先规定的范围内, 对末态的要求可以用末态约束条件来表示: ( ( ), ) 0 ( ( ), ) 0 1 1 f f f f g x t t g x t t 满足末态约束的状态集合称为目标集,记为M,即: { ( ); ( ) , ( ( ), ) 0, ( ( ), ) 0} 1 f f 2 f f n f f M x t x t R g x t t g x t t 至于末态时刻,可以事先规定,也可以是未知的。 有时初态也没有完全给定,这时,初态集合可以类似地用初态约束来表示。 1.绪论-最优控制问题的提法 3:容许控制 在实际控制问题中,大多数控制量受客观条件的限制,只能在一定范围内取 值,这种限制通常可以用如下不等式约束来表示: 0 u(t) umax 或ui i 1,2 p 上述由控制约束所规定的点集称为控制域U,凡在t0 -tf上有定义,且在控制域U 内取值的每一个控制函数u(t)均称为容许控制。 4:性能指标 通常情况下,最优控制问题的性能指标形如: f t t f f J x t t F x t u t t dt 0 ( ( ), ) ( ( ), ( ), ) 其中第一项是接近目标集程度,即末态控制精度的度量,称为末值型性能指标。 第二项称为积分型性能指标,它能反映控制过程偏差在某种意义下的平均或控制 过程的快速性,同时能反映燃料或能量的消耗。 1.绪论-最优控制问题的提法 5:最优控制的提法 已知受控系统的状态方程及给定的初态 X (t) f (X (t),u(t),t) ( ) (0) X t0 X 规定的目标集为M,求一容许控制u(t)∈U,t∈ [t0 ,tf ],使系统从给定的初态出发, 在t f >t0 时刻转移到目标集M,并使性能指标 f t t J x t f t f F x t u t t dt 0 ( ( ), ) ( ( ), ( ), ) 为最小。 这就是最优控制问题。 如果问题有解,记为u*(t), t∈ [t0 ,tf ],则u*(t)叫做最优控制(极值控制),相应的轨 线X*(t)称为最优轨线(极值轨线),而性能指标J*=J(u*(·))则称为最优性能指标。 1.绪论-最优控制问题的提法

】,绪论-最优控制问题的应用类型 1.绪论-最优控制向题的应用类型 1绪论~最优控制门题的应用类型 买普琴霜香雾。限重要的一个州愿是总性能指标,性发清标被北面学形 按护制系统的用途不同,所选释的性能指标不用。常见的有: 4:战州调节器 1a最中时闻控制 状志。 1)积分型性能指标J一X,a,地 J%,-%- 线性调节卷的性能指标为:一心三 这样的量代控制间题为检静朗日何思。 2最小物料清耗移制 知取后的性能指标为一三q油 2》锋物型性能指标J-可X化从,1 相略绝说,控刺单阳与燃料消样量成正比。最小燃料消托阿题的性能指标为 u有约束的性能指标为 J-文片r'een+'ot J-lmnld 式中Q和R是正定彩体 这种性能指标只是对手系候在达过程结束时的路溶状志灵出了菱求,而对干 一般形式。有展时问线性调竹客性候指标: 3最小能量挖刺 3)复合登性能瑞标J-,M,CF,w中 exa+inman 设标量授制函数的与所消耗的功本成正比。则敏小能量控制题的性能指标分 这样的量优控制闻题为该尔扎闻题。 无果时倒线件清器性能泰标一贴r”eQ0+0种 通过适当变热。拉格朝日材腿和迈哪尔科速可以服转热。 J-心t P20,Q0.R0,均为对格如仅能件. 1绪论-最优控制问题的应用类型 1绪论-最优控制何题的应用类型 2.数学准备-函数极值问题 5台提特最踪器 降7整药可选收他不网形 一套麦量卧量领恤风■ 获赛整素究?可院法近日标钱似这种系线格为北去露 释影无福红,在点为处有银么的要条 -C-xofaron-x.un-om 1)皮能反映时系统的主要技术条件要求 公=2l6,=0 £=gl=0 C0.R0,购为对将南仅影阵. 2)授于对量优控刺进行求解 í(xx2)取服小值的充分条件为: 着要求系统输出的,寒或尽可能核近日标轨连间,则这种系统称为输出综透, 其攻的性能高标为: 3)所导出的量优控刺易干工程实规 a+244+a广0 J-C-,ufG-o-um e C20,R0,均为时称如仅电年. 3
3 设计最优控制系统时,很重要的一个问题是选择性能指标,性能指标按其数学形 式可分为如下三类: 1)积分型性能指标 f t t J F X t u t t dt 0 [ ( ), ( ), ] 这样的最优控制问题为拉格朗日问题。 2)终值型性能指标 [ ( ), ] f f J X t t 这种性能指标只是对于系统在动态过程结束时的终端状态提出了要求,而对于 整个动态过程中系统的状态和控制的演变未作要求。这样的最优控制问题为迈 耶尔问题。 3)复合型性能指标 f t t J X t f t f F X t u t t dt 0 [ ( ), ] [ ( ), ( ), ] 这样的最优控制问题为波尔扎问题。 通过适当变换,拉格朗日问题和迈耶尔问题可以相互转换。 1.绪论-最优控制问题的应用类型 按控制系统的用途不同,所选择的性能指标不同,常见的有: 1:最小时间控制 f t t f J t t dt 0 1 0 2:最小燃料消耗控制 粗略地说,控制量u(t)与燃料消耗量成正比,最小燃料消耗问题的性能指标为: f t t J u t dt 0 | ( ) | 3:最小能量控制 设标量控制函数u 2 (t)与所消耗的功率成正比,则最小能量控制问题的性能指标为: f t t J u t dt 0 ( ) 2 1.绪论-最优控制问题的应用类型 4:线性调节器 给定一个线性系统,其平衡状态X(0)=0,设计的目的是保持系统处于平衡状态, 即这个系统应能从任何初始状态返回平衡状态。这种系统称为线性调节器。 线性调节器的性能指标为: f t t n i i J x t dt 0 1 2 ( ) 加权后的性能指标为: f t t n i i i J q x t dt 0 1 2 ( ) 对u(t)有约束的性能指标为: f t t T T J X t QX t u t Ru t dt 0 [ ( ) ( ) ( ) ( )] 2 1 式中Q和R都是正定加权矩阵。 一般形式,有限时间线性调节器性能指标: f t t T T f f T J X t PX t X t QX t u t Ru t dt 0 [ ( ) ( ) ( ) ( )] 2 1 ( ) ( ) 2 1 无限时间线性调节器性能指标: 0 [ ( ) ( ) ( ) ( )] 2 1 t T T J X t QX t u t Ru t dt P≥0,Q≥0,R>0,均为对称加权矩阵。 1.绪论-最优控制问题的应用类型 5:线性跟踪器 若要求状态X(t)跟踪或尽可能接近目标轨迹Xd (t),则这种系统称为状态跟踪器, 其相应的性能指标为: f t t T d T J X t X d t Q X t X t u t Ru t dt 0 [ ( ) ( )] [ ( ) ( )] ( ) ( )] 2 1 Q≥0,R>0,均为对称加权矩阵。 若要求系统输出y(t)跟踪或尽可能接近目标轨迹yd (t),则这种系统称为输出跟踪器, 其相应的性能指标为: f t t T d T J y t yd t Q y t y t u t Ru t dt 0 [ ( ) ( )] [ ( ) ( )] ( ) ( )] 2 1 Q≥0,R>0,均为对称加权矩阵。 1.绪论-最优控制问题的应用类型 除了上述几种应用类型外,根据具体工程实际的需要,还可以选取其他不同形 式的性能指标,在选取性能指标时需注意: 1)应能反映对系统的主要技术条件要求 2)便于对最优控制进行求解 3)所导出的最优控制易于工程实现 1.绪论-最优控制问题的应用类型 一:多变量函数极值问题 设二元函数f(x1 ,x2 ),在点(x1 *,x2 *)处有极值f(x1 *,x2 *)的必要条 件为: 0 ( , ) * ( , ) * 2 * 1 1 1 2 1 x x x f x x x f 0 ( , ) * ( , ) * 2 * 2 1 1 2 2 x x x f x x x f f(x1 *,x2 *)取极小值的充分条件为: ( ) 2 ( ) 0 2 2 * 1 2 2 * 1 * 1 1 1 2 2 2 f x x x f x x x x f x x x ( ) 0 2 1 * * * * 1, 2 1 2 2 2 1 1 1 2 x x f f f f x x x x x x x x x x 或 2.数学准备-函数极值问题
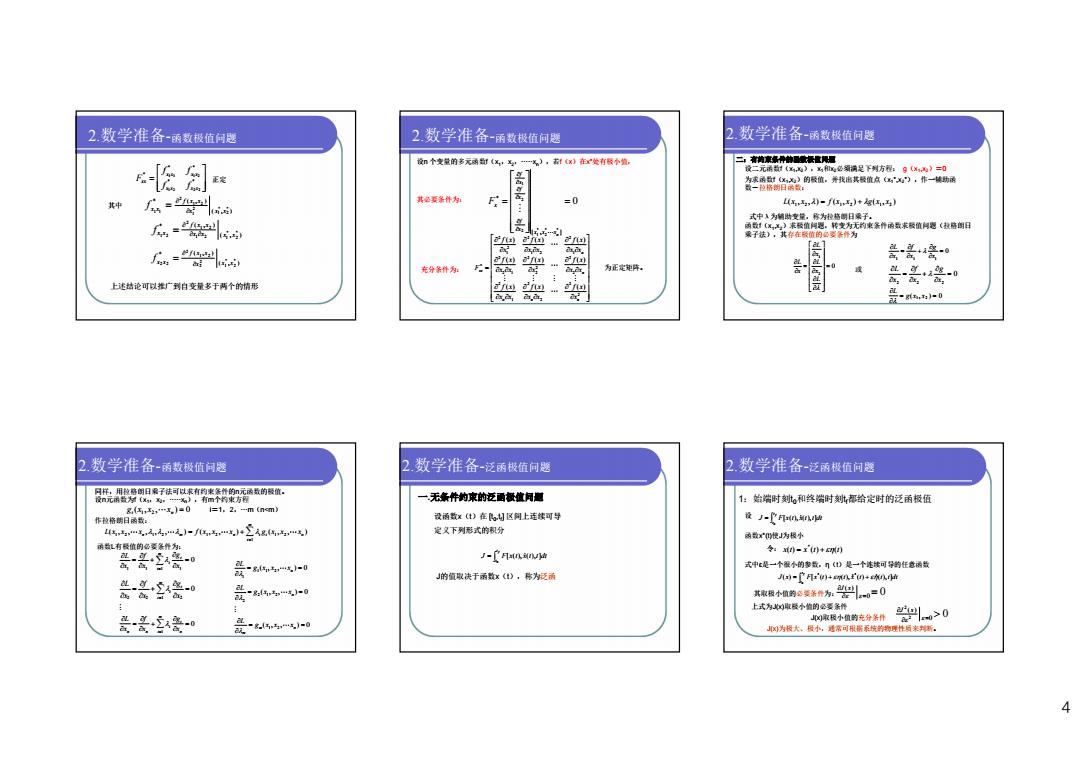
2数学准备-函数极值问题 2数学准备-函数极值问题 2数学准备-函数极值问题 n个变量的多元动《无:%:-%),x)在r绘有餐个幢: 股 户院总装精根时方品。,0 资整弱密音的餐值。并我高北餐值点国”,作一博商 其。 - 其色要条件为: F= =0 ,2-f)+, 式中1为销助安量。称为拉格明日采子。 =器 两数1(x,多)求餐值闻愿。转变为无约束条件函数求酸值问愿《社格朗日 [8 20 采子法),其存在顾值的必菱条作为 武 「1 人=lhs A 是熹毫 充分条件为: 为正定矩阵 上述结论可以推广到自变量多于两个的情形 已I1 a ie 及"84)-0 2.数学准备-丽数极值问避 2.数学准备-泛函极值问题 2数学准备-泛丽极值问题 册阳子祛可以有穷嘉利的吸。 一无条件的束的泛面餐值问息 1:始端时刻。和终端时刻呲都给定时的泛函极值 g国,2x=0 =1.2,-m(nm) 作拉格朗日两数: 设函数x()在区阿上连续可导 後-了Fn即w 4空 定久下列形式的积分 两数x四使J为极小 函数L有餐值的必菱条件为: J-文am0w0 令0-宝+W0 受--0 式中E是一个餐小的参数。】《D是一个连续可异约任意函数 J的值取决于函数x(),称为泛函 是-头尝 -广凡'e)+fm+nh CL 式取极值的爱华件为世L0=0 上式为回餐小恤的必要条作 是毫爱 远”8-0 )取极小值的充分条件 u>0 为极大。极小,透席可根据系坑的物理性质来判新。 4
4 * * * * * 1 2 2 2 1 1 1 2 x x x x x x x x xx f f f f F 正定 ( , ) * ( , ) * 2 * 1 2 1 1 2 2 1 1 x x x f x x x x f ( , ) * ( , ) * 2 * 1 2 1 1 2 2 1 2 x x x x f x x x x f ( , ) * ( , ) * 2 * 1 2 2 1 2 2 2 2 x x x f x x x x f 其中 上述结论可以推广到自变量多于两个的情形 2.数学准备-函数极值问题 设n 个变量的多元函数f(x1 ,x2 ,·····xn ),若f(x)在x*处有极小值, 其必要条件为: 0 [ , ] * * * 2 * 1 2 2 1 n x x x x f x f x f Fx 充分条件为: 2 2 2 2 1 2 2 2 2 2 2 2 1 2 1 2 1 2 2 2 1 2 * ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) n n n n n xx x f x x x f x x x f x x x f x x f x x x f x x x f x x x f x x f x F 为正定矩阵。 2.数学准备-函数极值问题 二:有约束条件的函数极值问题 设二元函数f(x1 ,x2 ),x1 和x2 必须满足下列方程: g(x1 ,x2 )=0 为求函数f(x1 ,x2 )的极值,并找出其极值点(x1 *,x2 *),作一辅助函 数-拉格朗日函数: ( , , ) ( , ) ( , ) 1 2 1 2 1 2 L x x f x x g x x 式中λ为辅助变量,称为拉格朗日乘子。 函数f(x1 ,x2 )求极值问题,转变为无约束条件函数求极值问题(拉格朗日 乘子法),其存在极值的必要条件为 0 2 1 L x L x L x L 或 0 1 1 1 x g x f x L 0 2 2 2 x g x f x L ( 1 , 2 ) 0 g x x L 2.数学准备-函数极值问题 同样,用拉格朗日乘子法可以求有约束条件的n元函数的极值。 设n元函数为f(x1 ,x2 ,·····xn ),有m个约束方程 ( , , ) 0 gi x1 x2 xn i=1,2,···m(n<m) ( , , , , , ) ( , , ) ( , , ) 1 2 1 1 2 1 2 1 2 i n m i n m n i L x x x f x x x g x x x 作拉格朗日函数: 函数L有极值的必要条件为: 0 1 1 1 1 x g x f x L i m i i 0 2 2 1 2 x g x f x L i m i i ( , , ) 0 1 1 2 1 n g x x x L ( , , ) 0 2 1 2 2 n g x x x L ( , , ) 0 1 2 m n m g x x x L 0 1 n i m i i n n x g x f x L 2.数学准备-函数极值问题 一.无条件约束的泛函极值问题 设函数x(t)在 [t0 ,tf ] 区间上连续可导 定义下列形式的积分 J F x t x t t dt f t t [ ( ), ( ), ] 0 J的值取决于函数x(t),称为泛函 2.数学准备-泛函极值问题 1:始端时刻t0 和终端时刻t f 都给定时的泛函极值 设 J F x t x t t dt f t t [ ( ), ( ), ] 0 函数x*(t)使J为极小 令: ( ) ( ) ( ) * x t x t t 式中ε是一个很小的参数,η(t)是一个连续可导的任意函数 J x F x t t x t t t dt f t t ( ) [ ( ) ( ), ( ) ( ), ] 0 * * 其取极小值的必要条件为: 0 0 ( ) J x 上式为J(x)取极小值的必要条件 J(x)为极大、极小,通常可根据系统的物理性质来判断。 0 0 ( ) 2 2 J x J(x)取极小值的充分条件 2.数学准备-泛函极值问题
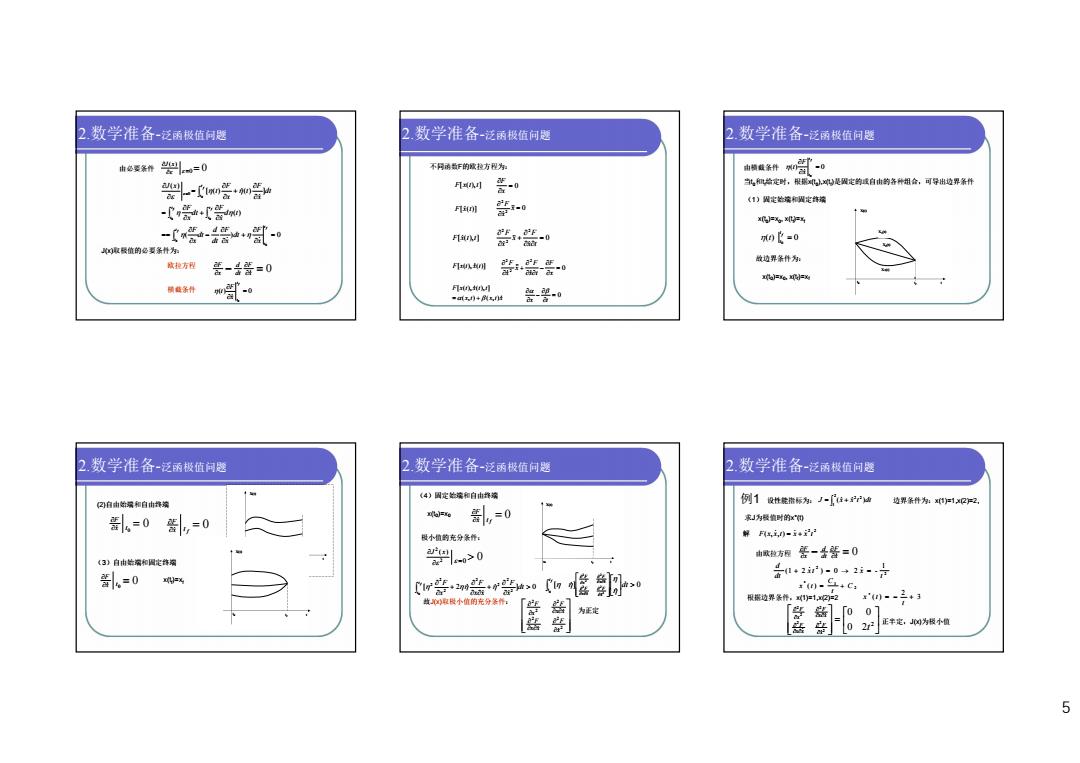
2数学准备-泛函极值问题 2数学准备-泛函极值问题 2数学准备-泛函极值问题 由色要作=0 不同函最F的城拉方程为 斜-受·m营 F 0 乳们始定时,根据是婴定约度自由的各种组金,可导出垃界条件 《1)型定站端和州定锋滨 -r+若 F凡0 器0 x(=Xxx 受搭w置0 F 带器 0北=0 取酸值的色要条样为 敏边界条件为: 威拉方程菩-号菩=0 F川 器营0 6g= w F凡iw 警碧0 2数学准备-泛丽极值问题 2.数学准备-泛函极值问题 2.数学准备-泛丽极值问题 《4)国定始端和白由择端 闪白由始端和自由择端 例1设性能带际为:J在+通 1 迹界条件为:12 引。=0,=0 ,=0 求J为极慎时的x罚 假小植的充分条作: 解F,)-4 《3》自由始深和国定锋溶 空-lw>0 由欧拉方程普一圣普=0 d =0 =% 420→2月 r普·2n监rh0 如修卧… .54c, 站取假小值的充分条: 根据边界条作。11,=2 盘 02 正半定,J侧为极小植 5
5 ( ) 0 ( ) [ ( ) ( ) ] ( ) 0 0 0 0 0 0 f f f f f t t t t t t t t t t x F dt x F dt d dt x F d t x F dt x F dt x F t x F t J x J(x)取极值的必要条件为: 0 x F dt d x F ( ) 0 0 f t t x F t 欧拉方程 横截条件 0 0 ( ) J x 由必要条件 2.数学准备-泛函极值问题 不同函数F的欧拉方程为: F[x(t),t] 0 x F F[x(t)] 0 2 2 x x F F[x(t),t] 0 2 2 2 x t F x x F F[x(t), x(t)] 0 2 2 2 x F x t F x x F x t x t x F x t x t t ( , ) ( , ) [ ( ), ( ), ] 0 x t 2.数学准备-泛函极值问题 当t0 和t f 给定时,根据x(t0 ),x(tf)是固定的或自由的各种组合,可导出边界条件 (1)固定始端和固定终端 ( ) 0 0 f t t t x(t0 )=x0 , x(tf)=xf 故边界条件为: x(t0 )=x0 , x(tf)=xf X(t) X1 (t) X2 (t) X3 (t) t0 tf t ( ) 0 0 f t t x F t 由横截条件 2.数学准备-泛函极值问题 (2)自由始端和自由终端 0 0 x t F 0 f x t F X(t) t0 tf t (3)自由始端和固定终端 0 0 x t F x(tf)=xf X(t) t0 tf t 2.数学准备-泛函极值问题 (4)固定始端和自由终端 x(t0 )=x0 0 f x t F X(t) t0 tf t 极小值的充分条件: 0 0 ( ) 2 2 J x [ 2 ] 0 2 2 2 2 2 2 2 0 dt x F x x F x t f F t [ ] 0 2 2 2 2 2 2 0 dt x F x x F x x F x F t t f 故J(x)取极小值的充分条件: 2 2 2 2 2 2 x F x x F x x F x F 为正定 2.数学准备-泛函极值问题 例1 设性能指标为: J (x x t )dt 2 1 2 2 边界条件为:x(1)=1,x(2)=2, 求J为极值时的x*(t) 解 2 2 F(x, x,t) x x t 由欧拉方程 0 x F dt d x F 2 2 1 (1 2 ) 0 2 - t x t x dt d 2 * 1 ( ) C t C x t 根据边界条件,x(1)=1,x(2)=2 3 2 ( ) * t x t 2 0 2 0 0 2 2 2 2 2 2 t x F x x F x x F x F 正半定,J(x)为极小值 2.数学准备-泛函极值问题
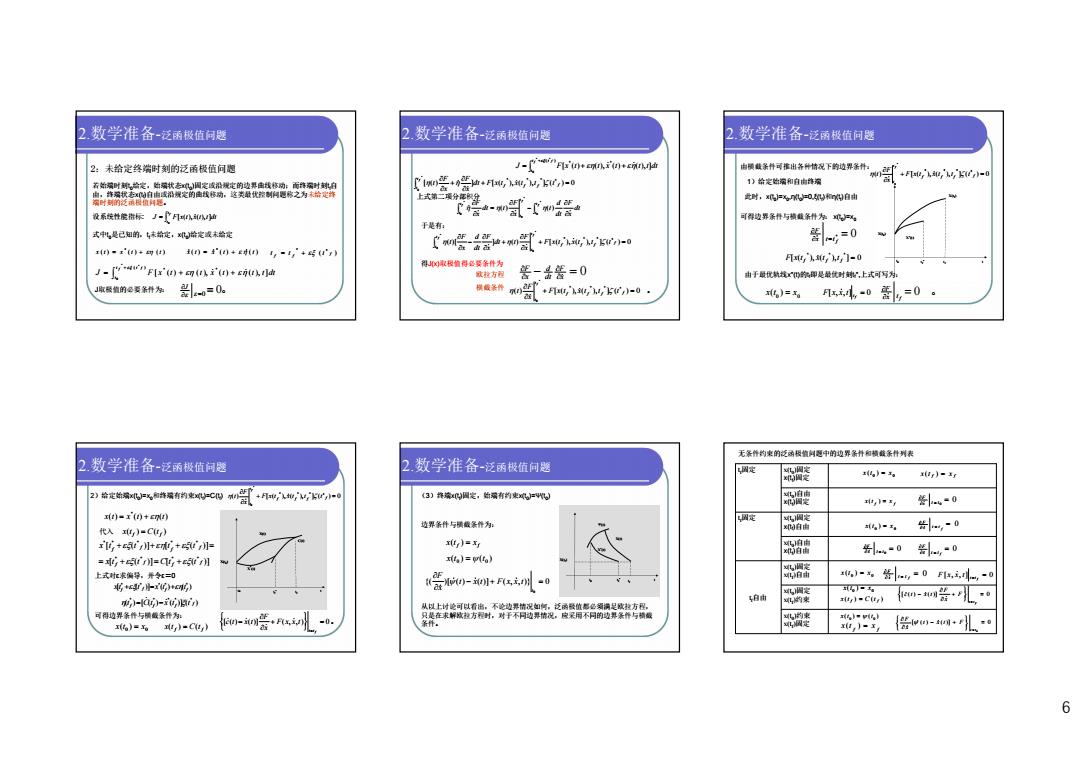
2数学准备-泛函极值问题 2数学准备-泛函极值问题 2数学准备-泛函极值问题 2:未给定终端时刻的泛函极值问题 -F'th emni(ncitldr 由横维条件可推出各种情况下的边界条件 wn+,k,'50-0 着始时。定,始状态国定或沿规定的边由线修:面时球白 10◆-电,1电,M,5,-0 1》给定始溶和自向许漏 贵整盟电动城定的仿动这关处优签州题你之为瑞定瑞 上式第二项分尾樱生 女时,邓=%-04自由 投系统性能指标J-广F种 可得边舞条件与精酸条什为% 于是有: 式中,是己知的。未给定,x哈定或末给定 +,r,h,'5t-0 -=0 x)▣x')+) 0·4'0+),-,+写) 得取极植得必要条件为 F,h,,门-0 J-4"FIro+go+ruh 我拉方湿 普-出箬=0 由手最优轨找四你御是最优时球,上式可写为: J取酸的要条为 0=0。 横酸条件 +F'h5r-0- 。》=6 -0=0。 无条作约束的泛动极值问中的边界条和横条列表 2数学准备-泛函极值问题 2.数学准备-泛函极值问题 州定 品餐 %=。 xu)-y 2》给定兰4和锋有的电0-C和置。 (3)择编国定,始端有约束。=州。 艘 ,, 装w-0 x(t)-x(0+cnn) 定 边界条件与横截条作为: 代入,)-Cy) 6图 f%-玉4 告…,-0 rg+e+e可+5= x(tt)=x $田 -0装,-0 =耶+tr川=q可+5月 )=a】 上式求编绿。开红=0 g+c4,+c》 告-0Fu小-0 器 ,)=。 {,=0F,小,-0 国宽 w-ai-ivabin 的来 ,l=Cr) e-om告-r儿,。 从以上讨论可以看出。不论边郭情况如南。泛两龄值影必溺满足成拉方程, 可得边界条作与桶截条作为: =0 只是在求解城拉方程时。对干不可边界棉况。应采用不同的边界柔作与精截 的来 到4▣6 条件 电定 偿wen-儿 6
6 2:未给定终端时刻的泛函极值问题 若始端时刻t0 给定,始端状态x(t0 )固定或沿规定的边界曲线移动;而终端时刻t f 自 由,终端状态x(tf)自由或沿规定的曲线移动,这类最优控制问题称之为未给定终 端时刻的泛函极值问题。 设系统性能指标: J F x t x t t dt f t t [ ( ), ( ), ] 0 式中t0 是已知的,t f 未给定,x(t0 )给定或未给定 ( ) ( ) ( ) * x t x t t ( ) ( ) ( ) * x t x t t ( ) * * f f f t t t J F x t t x t t t dt f f t t t [ ( ) ( ), ( ) ( ), ] ( ) * * * * 0 J取极值的必要条件为: J 0 0。 2.数学准备-泛函极值问题 [ ( ) ] [ ( ), ( ), ] ( ) 0 * * * * * 0 f f f f t t dt F x t x t t t x F x F t f 上式第二项分部积分 * 0 * 0 * 0 ( ) ( ) f f f t t t t t t dt x F dt d t x F dt t x F 于是有: ( )[ ] ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0 * 0 f f f f t t t t F x t x t t t x F dt t x F dt d x F t f f 得J(x)取极值得必要条件为 0 x F dt d x F 欧拉方程 横截条件 ( ) [ ( ), ( ), ] ( * ) 0 。 * * * * 0 f f f f t t F x t x t t t x F t f J F x t t x t t t dt f f t t t [ ( ) ( ), ( ) ( ), ] ( ) * * * * 0 2.数学准备-泛函极值问题 由横截条件可推出各种情况下的边界条件: 1)给定始端和自由终端 X(t0 ) t0 tf t X* (t) X(tf ) tf* 此时,x(t0 )=x0 ,η(t0 )=0,ξ(tf)和η(tf)自由 可得边界条件与横截条件为: x(t0 )=x0 * 0 f x t t F [ ( ), ( ), ] 0 * * * F x t f x t f t f 由于最优轨线x*(t)的t f 即是最优时刻t f*,上式可写为: 0 0 x(t ) x [ , , ] 0 f t F x x t F x t f 0 。 ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0 f f f f t t F x t x t t t x F t f 2.数学准备-泛函极值问题 2)给定始端x(t0 )=x0 和终端有约束x(tf)=C(tf) X(t0 ) t0 tf t X* (t) X(t) tf* C(t) ( ) ( ) ( ) * x t x t t 代入 ( ) ( ) f f x t C t [ ( )] [ ( )] [ ( )] [ ( )] * * * * * * * * * f f f f f f f f x t t C t t x t t t t 上式对ε求偏导,并令ε=0 ( ) [ ( ) ( )] ( ) * * * * * f f f f t C t x t t 可得边界条件与横截条件为: 0 0 x(t ) x ( ) ( ) f f x t C t [ ( ) ( )] ( , , ) 0。 f t t F x x t x F c t x t ( ) [ ( ), ( ), ] ( ) 0 * * * * * 0 f f f f t t F x t x t t t x F t f 2.数学准备-泛函极值问题 [ ( )] ( ) ( ) * * * * * f f f f x t t x t t (3)终端x(tf)固定,始端有约束x(t0 )=Ψ(t0 ) X(tf ) t0 tf t X* (t) X(t) tf* 边界条件与横截条件为: Ψ(t) f f x(t ) x ( ) ( ) 0 0 x t t {( )[ ( ) ( )] ( , , )} 0 0 t t x t F x x t x F 从以上讨论可以看出,不论边界情况如何,泛函极值都必须满足欧拉方程, 只是在求解欧拉方程时,对于不同边界情况,应采用不同的边界条件与横截 条件。 2.数学准备-泛函极值问题 0 0 x (t ) x f f x (t ) x f f x (t ) x 0 0 x t t F 0 0 x(t ) x 0 f x t t F 0 0 x t t F 0 f x t t F 0 0 x (t ) x 0 f x t t F [ , , ] 0 f t t F x x t 0 0 x(t ) x ( ) ( ) f f x t C t [ ( ) ( )] 0 f t t F x F c t x t ( ) ( ) 0 0 x t t f f x (t ) x [ ( ) ( )] 0 0 t t t x t F x F tf 固定 x(t0 )固定 x(tf)固定 x(t0 )自由 x(tf)固定 tf 固定 x(t0 )固定 x(tf)自由 x(t0 )自由 x(tf)自由 tf 自由 x(t0 )固定 x(tf )自由 x(t0 )固定 x(tf )约束 x(t0 )约束 x(tf )固定 无条件约束的泛函极值问题中的边界条件和横截条件列表

2数学准备-泛函极值问题 2数学准备-泛函极值问题 2数学准备-泛函极值问题 例2 求使性能密标 J-Pasgta h边界条作,)=C,》 i=a x(1)=a+b 为假小时的最优轨r间.设0=1.=C,C=2以t末给定. 与+1=2-4 解袋能长也号 ,= x F0-1+2 x0J=x《0)s=1,0=at*1 厥拉方程为: 横截条件 普-孟普=0 -m·儿 了=-+h=90 0- d「主 …时。 哥 1+F+…+ -0 +Fe· 解得()1a=1 x()=1+1 2数学准备-向量泛函极值问题 2数学准备-向量泛雨极值问题 2.数学准备-有钓束条件的泛函极值问趣 在上面所时论约公式中,都假定x是1量。但是。所有会 对于始网时辣。和许鸡时封都给定时,横戴条骨 式幕可推广到峰变绿情况 置 赛精轻受装竿锅化.受 设性能密标J-广F:,i放 1.代数方程约来 x(t) 式中 设J-C4w 式中 )- 物来方程G(红,)-0。eRG。e:m<。 胸地W广泛通人-F,+2EGaw1。R“ 则玻拉方湿为菩一告瓷=0 对于末给定择端时辣时的横截条作为: 《1)给定始滨和择端有榨来: (2)给定锋和始有来 ◆地量函数任,意人)-Fx,)+2G(,) 式中 eo-r器儿 {二w-f 0. .=ra+sya+倍ya=0 分富职分 7
7 例2 求使性能指标 J x dt f t t 0 2 1 (1 ) 2 为极小时的最优轨线x*(t)。设x(0)=1,x(tf)=C(tf),C(tf)=2-t, tf 未给定。 解 显然,所给出的性能指标就是x(t)的弧长,也就是说,要求从x(0)到直 线C(t)的弧长未最短。 t x(t) c(t) 2 x( 0) x*(t) x(t) 0 2 1 ( , , ) (1 ) 2 F x x t x 欧拉方程为: 0 x F dt d x F 0 ( 1 ) 0 2 1 2 x x dt d c 。 x x 2 1 (1 ) 2 2.数学准备-泛函极值问题 2 2 2 1 a c c x x a x (t ) at b 这是一个x(t0 )固定,x(tf)约束情况下的极值问题。 由边界条件 x(t0 )=x(0) b=1,x(t)=at+1 横截条件 [ ( ) ( )] 0 f t t F x F c t x t (1 ) 0 (1 ) [ 1 ] 2 1 2 1 2 f t t x x x x 解得 x (t f ) 1 a 1 x * (t ) t 1 。 t x(t) c(t) 2 x( 0) x*(t) x(t) 0 2.数学准备-泛函极值问题 由边界条件 ( ) ( ) f f x t C t f f t 1 2 t 2 1 * t f 2 2 0 2 * * 2 1 2 1 (1 ) J x dt t x(t) c(t) 2 x(0) x*(t) x(t) 0 2.数学准备-泛函极值问题 在上面所讨论的公式中,都假定x是1维变量,但是,所有公 式都可推广到n维变量的情况 设性能指标 J F x x t dt f t t ( , , ) 0 式中 ( ) ( ) ( ) ( ) 2 1 x t x t x t x t n 则欧拉方程为 0 x F dt d x F 式中 n x F x F x F x F 2 1 。 n x F x F x F x F 2 1 2.数学准备-向量泛函极值问题 对于始端时刻t0 和终端时刻t f 都给定时,横截条件 ( ) 0 0 f t t T x F t 式中 ( ) ( ) ( ) ( ) 2 1 t t t t n 对于未给定终端时刻t f 时的横截条件为: (1)给定始端和终端有约束: [ ( ) ( )] 0 f t t T F x F c t x t (2)给定终端和始端有约束 [ ( ) ( )] 0 。 0 t t T t x t F x F 2.数学准备-向量泛函极值问题 在实际问题中,对应泛函极值的最优轨线x*(t)通常不能任意选取,而受着 各种约束。求泛函在等式约束下的极值,称为条件泛函极值问题。 1.代数方程约束 设 J F x t x t t dt f t t [ ( ), ( ), ] 0 约束方程 G ( x , t ) 0 n x R m G R m n 构造增广泛函 J F x x t G x t dt T t t a f [ ( , , ) ( , )] 0 m R 令纯量函数 L(x, x, ,t) F(x, x,t) G(x,t) T 0 0 J x x dt f t t T L T x L T x L a 分部积分 2.数学准备-有约束条件的泛函极值问题

2数学准备-有约束条件的泛函授值向题 2数学准备-有约束条件的泛丽极值问题 2数学准备-有约束条件的泛函极值问题 上秘-4倍y+G'ah+了a=0 2:微分方程约来 3:积分方程约桌 最J-下,d 约来方型G-eGR”c为-常数 史锈登产。旅上试线之,度闲时满足下毯威拉方,的 设J一Fi陆 设2(t)▣G(x,,) 电¥件:G(x,,0-0.GcR- 则G(x,,)-2()-0 Z(t)-0 Zu,)-e 歌拉方程: 是-出是=0熹+(1-菩=0 设纯绿两数红,年石,)=F风红,名)+严Gx,主) 间 L=F+(G-2) 的来方根:G(¥,)。0 欧粒方程丝一圣各=0 拉方程普-兰兰=0一警-是鲁=0-0 横酸条作: (卧y6xk=0 ÷答+竖y-÷普-倍y1=0 的桌方程2)-G(3,,)Z0。》-0Zu,)-e 利用横截条件,根据始端状老心)阳许鸡状志x的不月情况,可以导 的束条情G(x,,)-0 横益务件 供Yk-0 出具修的迹界条件和横酸条件,其时论过程和结论与无的束条件的泛 保数条件 可昆,对干有的业条州的泛函经值问题。可采用妆麻朗日聚子法将其转化为无 两极物阿是和同。 (侍y6:=0s(s+年了作=0 密。在险条你议,业方微不多 3用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 设系统状志方程 一初始时刻及始端状态。哈定,给定,终端自由 可。受-r4,+受ra贸-0 构通增广泛稀 i-f八此,) 为使上式成立,应同时满足下列方程 能指标J一电,A]F油 .-,小'F,+V红4-d 表方8作鞋方同要 令哈击尔顿两数: 状志方程 毁 式中R。B解为纯绿雨最 H品么0-F+f4,a) 控制方程 0… 量优控刺闻愿就是寻求最优控制')及量优状态轨连” 则上-,M-%,20-2 机酸条丹 尝-好4心 使性能需标取餐值 岛尝学r+尝-0r-a-轴0 注意孙: 小 ga袖-中-文亚袖,-● 对于丙编圆定的情况下精截条件心一。,一 8
8 0 0 0 f f t t T x L t t T T x L dt d T x L x G dt x 由于δx, δλ相互独立,为使上式成立,应同时满足下述欧拉方程,约 束方程和横截条件: 欧拉方程: 0 x L dt d x L 0 x F dt d T x G x F 约束方程: G ( x , t ) 0 横截条件: 0 0 f t t T x L x 利用横截条件,根据始端状态x(t0 )和终端状态x(tf)的不同情况,可以导 出具体的边界条件和横截条件,其讨论过程和结论与无约束条件的泛 函极值问题相同。 2.数学准备-有约束条件的泛函极值问题 2:微分方程约束 设 J F x x t dt f t t ( , , ) 0 约束条件:G ( x , x, t ) 0 m G R 设纯量函数 L(x, x, ,t) F(x, x,t) G(x, x,t) T 欧拉方程 0 x L dt d x L 0 T x G dt d x F dt d T x G x F 约束条件 G ( x , x , t ) 0 横截条件 0 0 f t t T x L x 0 0 f t t T x T G x F x 2.数学准备-有约束条件的泛函极值问题 3:积分方程约束 设 J F x x t dt f t t ( , , ) 0 约束方程 G x x t dt c f t t ( , , ) 0 m G R c为一常数 设 Z (t ) G ( x , x, t ) 则 G ( x , x, t) Z (t) 0 ( ) 0 Z t 0 Z t c ( f ) 令 z x x z x x L F (G Z) T 欧拉方程 0 x L dt d x L 0 x L dt d x L 0 约束方程 Z (t ) G ( x , x, t ) Z (t 0 ) 0 Z t c ( f ) 横截条件 0 0 f t t T x L x 可见,对于有约束条件的泛函极值问题,可采用拉格朗日乘子法将其转化为无 约束条件的泛函极值问题进行求解。在不同边界条件情况下,欧拉方程不变, 只是边界条件及横截条件不同。 2.数学准备-有约束条件的泛函极值问题 设系统状态方程: x f (x,u,t) 性能指标: f t t f f J x t t F x u t dt 0 [ ( ), ] ( , , ) 式中 n p x R u R 和F为纯量函数 最优控制问题就是寻求最优控制 ( ) * u t 及最优状态轨迹 ( ) * x t 使性能指标J取极值. 3.用变分法求解最优控制问题 一.初始时刻 及始端状态 给定 t0 x(t0 ) , t f给定,终端自由 构造增广泛函 f t t T a f f J x t t F x u t f x u t x dt 0 [ ( ), ] { ( , , ) [ ( , , ) ]} 令哈密尔顿函数: H (x,u, ,t) F(x,u,t) f (x,u,t) T 则 f t t T J a x t f t f H x u t x dt 0 [ ( ), ] [ ( , ,, ) ] ( ) [( ) ( ) ( ) ] 0 0 x x dt H u u H x x H x x J T T T T T t t t t T a f f 注意到: f f f t t t T t T t t T xdt x xdt 0 0 0 x (t 0 ) 0 3.用变分法求解最优控制问题 ( ) [( ) ( ) ( ) ] 0 0 x dt H u u H x x H x a x J T T T t t t t T f f 为使上式成立,应同时满足下列方程: 欧拉方程(伴随方程) x H 状态方程 H x 控制方程 0 u H 横截条件 f f f t t t T x t x t x x x ( ) ( ) ( ) 0 0 0 对于两端固定的情况下横截条件 f f x(t ) x , x(t ) x 0 0 3.用变分法求解最优控制问题

3.用变分法求解最优控制问题 3用变分法求解最优控制问题 3用变分法求解最优控制问题 例1 授系统状志方程为 主()=-0+) i-x-2 跗 二.初始时刻1及始端状态4)给定,1y给定终端约束 0的垃界条作为0-l北,-0 克55-w0+ 设许瑞的来方程为,1-,月-0MGR 求最优校制)使下列作伦密标 -6E百5a0o, 构造州广泛: J'+恤 人.-,月+PM,月+了红此+V红,k-d 为最小 由边舞保作可0-1中,》-0 解作哈密尔顺雨数日-++水-+ 0-E:业点w5 =+M,+广H,-d 聚拉方根-翌 -4 式神E时 无▣-x+无 修制 控制方程 u+人m0 2a.e,E465 =0 1 状志方程 ,-x+■ 5-eBEw 取极植的必要条件是 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 正剩方程 状态方程 三初始时刻。及始端状态心,)给定,1,自由,终端约束 用变分法求解最优解的必要条件: 设体端的来为,1-0 藏拉方型 胸造增广泛两J.-可电,M,小+电,,小+1Hx,2- 性能指标J-e1u,h,1小F,恤 控制方程 熙… 园。一0得取极慎的冬要条件本 H,,0-F《a,,0+21,0 正则方程 边条和精截条件化。)-,,月-0 拉防程要0 系埃方程-八红,, ,-喂尝 盛-,w小0 约来条件4-,M,h,1-0 ,尝尝 五到方81 g 尝… 控刺方程 … 9
9 例 1 设系统状态方程为 x(t) x(t) u(t) x(t) 的边界条件为 x(0) 1, x(t f ) 0 求最优控制 u(t) 使下列性能指标 f t J x u dt 0 2 2 ( ) 2 1 为最小 解: 作哈密尔顿函数 ( ) ( ) 2 1 2 2 H x u x u 欧拉方程 x 控制方程 0, 0 u u H 状态方程 x x u H x , x H 3.用变分法求解最优控制问题 x x x ( ) (0) 2 2 1 [( 2 1) ( 2 1) ] (0) 2 2 1 2 2 2 2 t t t t x e e x e e [( 2 1) ( 2 1) ] (0) 2 2 1 ( ) (0) 2 2 1 2 2 2 2 t t t t e e x e e 消除u 由边界条件 x(0) 1, x(t f ) 0 f f f f t t t t e e e e 2 2 2 2 ( 2 1) ( 2 1) (0) 得最优控制 [( 2 1) ( 2 1) ]} ( 2 1) ( 2 1) { 2 2 1 2 2 2 2 2 2 2 t t t t t t t t e e e e e e e e u f f f f x x 1 1 1 1 3.用变分法求解最优控制问题 二. 初始时刻 及始端状态 给定 0 , 给定,终端约束. t ( ) 0 x t f t 设终端约束方程为 M[x(t f ),t f ] M[x(t f )] 0 q M R 构造增广泛函: f t t T f T J a x t f v M x t F x u t f x u t x dt 0 [ ( )] [ ( )] { ( , , ) [ ( , , ) ]} f t t T f T f x t v M x t H x u t x dt 0 [ ( )] [ ( )] { ( , ,, ) ]} 式中 q v R 0 [ ( ) ] [( ) ( ) ( ) ] 0 x dt H u u H x x H v x x M x J T T T t t t t T T a f f J取极值的必要条件是 3.用变分法求解最优控制问题 正则方程 欧拉方程 状态方程 x H H x 控制方程 0 u H 边界条件和横截条件 ( ) , 0 0 x t x [ ( )] 0 f M x t f t t T f v x M x t ( ) [ ( ) ] 3.用变分法求解最优控制问题 三. 初始时刻 及始端状态 给定 t0 x(t0 ) , t f 自由,终端约束 设终端约束为 M[x(t f ),t f ] 0 构造增广泛函 f t t T f f T J a x t f t f v M x t t H x u t x dt 0 [ ( ), ] [ ( ), ] [ ( , ,, ) ] 0 a J 得J取极值的必要条件为: 正则方程 x H H x 控制方程 0 u H 边界条件和横截条件 ( ) , 0 0 x t x M[x(t f ),t f ] 0 f t t T f v x M x t ( ) [ ( ) ] [ ] 0 f t t T t M v t H 3.用变分法求解最优控制问题 用变分法求解最优解的必要条件: 性能指标 f t t J x t f t f F x u t dt 0 [ ( ), ] ( , , ) H (x,u, ,t) F ( x,u,t) f ( x,u,t) T 系统方程 x f (x,u,t) 约束条件 ( ) , 0 0 x t x [ ( ), ] 0 f f M x t t 正则方程 H x x H 控制方程 0 u H 3.用变分法求解最优控制问题

条作边界条料和横戴条件 终端因定 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 终端自由 ,”品 例2已知系统找志方程为-0,o-】 0)-4eh6e 给定 终端钓束 g川-0,-尝· 求最优拉制:')使怪能指标了一心产(2+产边为最小 解本题为,给定,裤漏自由的销况 -i---- 终端因定 ”哥 边界条外与横鼓条料 H-e22◆2+2出 小山小”部0-。 终端自由 6》-x , 等 求得 i-v 5-1 t E+e6 i-22 6"不5-平“5-+w 自由 ,= ,,1-0 终端钓束 西 拉防程兴。 242a2-0→i-22w+i 最得级执拉制0广不E-。 -2x0--22u+w2 --l.7957ea-00591ena] 消至+2近-x-0 3用变分法求解最优控制问题 3.用变分法求解最优控制问题 3.用变分法求解最优控制问题 例3 慢不统的状老方程为 垃界采桥和横醛条科 H-2++4-+ -名 正防程”股名山。+ 0)-0+0.56-6+5-0 24-+4 40-e-0-*6 一-3卡4 -4-0.5名46-0 10明-0-0 与4-e-0-5 02-a-f 性能指标一2-开+24-油 BM 0-2-f-2乎 择端的来条件(2)+5红2-15 4m6 M-,2+524-15-0 4,i', M-24s,(4-15=0 认求使J一m的量优控制 控制方程 尝0+40小 2(2)-2-54-4 解本题为一始定锋端受均来的敏忧解例圆 20 U 2)--4:)+g u"+0 …++5+时 8-2+- 40-60-0 2(2)=x:(2)-2+5n°ce2+9, 2以-4吗+4 M-42)+52)-15=0 40ee-4+ 代队2.x2) 10
10 条件边界条件和横截条件 t f 给定 终端固定 终端自由 终端约束 t f 自由 终端固定 终端自由 终端约束 ( ) , 0 0 x t x f f f M[x(t )] 0 x(t ) x 0 0 x(t ) x ( ) ( ) f f x t t 0 0 x(t ) x 0 0 x(t ) x 0 0 x(t ) x 0 0 x(t ) x [ ( )] 0 f M x t f t T f v x M x (t ) [ ( ) ] f f x(t ) x f f t H t ( ) ( ) ( ) f f x t t f f t H t ( ) M[x(t f ),t f ] 0 f t t T f v x M x t ( ) [ ( ) ] f t t T f t M v t H t ( ) [ ] 例2 已知系统状态方程为 x u(t), x(0) 1 求最优控制 ( ) * u t 使性能指标 1 0 2 2 2 J e (x u )dt t 为最小 解 本题为 f t 给定,终端自由的情况 H e x u u t ( ) 2 2 2 正则方程: H x x H 控制方程 0 u H 得 x u t xe2 2 t t ue u u e 2 2 2 0 2(2 ) t t xe u u e 2 2 2 2(2 ) 消除u x 2x x 0 3.用变分法求解最优控制问题 t t x t c e c e (1 2) 2 (1 2) 1 ( ) t t u x c e c e (1 2 ) 2 (1 2 ) 1 (1 2) (1 2) 边界条件与横截条件 0 0 x(t ) x (0) 1, (1) 0 ( ) ( ) x x t t f f 求得 2 2 1 ( 2 1) ( 2 1) 2 1 e c 2 2 2 2 2 ( 2 1) ( 2 1) ( 2 1) e e c 最后得最优控制 [ ] ( 2 1) ( 2 1) 1 ( ) (1 2) 2 2 (1 2 ) 2 2 * t t e e e e u t 1.7957[ 0.0591 ] 2.4142 t 0.4142 t e e 3.用变分法求解最优控制问题 例3 设系统的状态方程为 1 2 x x x x u 2 2 x1 (0) 0 x2 (0) 0 性能指标 2 0 2 2 2 2 1 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1 J x x u dt 终端约束条件 x1 (2) 5x2 (2) 15 试求使 J min 的最优控制 解 本题为 t f 2给定 终端受约束的 最优解问题 ( ) 2 1 1 2 2 2 2 H u x x u u x u 1 2 2 2 2 ( ) 2 1 2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1 x x M x1 (2) 5x2 (2) 15 0 3.用变分法求解最优控制问题 正则方程 x x x x u H x 1 2 2 2 , 1 1 1 1 1 , 0, (t) c x H x H 2 1 2 2 1 2 2 , (t) c e c x H t 控制方程 2 2 1 0 u 0 u(t) c e c u H t x 2 (t ) x 2 (t ) u 2 3 2 1 2 1 x (t) c e c e c t t 1 3 2 1 4 2 1 x (t) c e c e c t c t t ( ) 2 1 1 2 2 2 2 H u x x u u x u 1 2 2 2 2 ( ) 2 1 2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1 x x M x1 (2) 5x2 (2) 15 0 3.用变分法求解最优控制问题 边界条件和横截条件 (0) 0, 0.5 0 x c2 c3 c4 c1 0.5c2 c3 0 ) ( ) ( ) ( ( ) ( ) 1 1 1 f T f f f v t x t M x t t 1 1 1 (2) x (2) 5 v c ) ( ) ( ) ( ( ) ( ) 2 2 2 f T f f f v t x t M x t t 1 2 2 2 2 ( 2 ) x ( 2 ) 2 5 v c e c 代入 (2), 1 x ( 2 ) 2 x 2 3 2 1 2 1 x (t) c e c e c t t 1 3 2 1 4 2 1 x (t) c e c e c t c t t 2 2 2 1 [ (2) 2] 2 1 [ (2) 5] 2 1 x x M x1 (2) 5x2 (2) 15 0 3.用变分法求解最优控制问题