3.5 结点电压法 1结点电压法 以结点电压为未知量列写电路方程分析 电路的方法。适用于结点较少的电路。 基本思想 选结点电压为未知量,则KVL自动满足 就无需列写KVL方程。各支路电流、电压可 视为结点电压的线性组合,求出结点电压后 便可方便地得到各支路电压、电流。 KVL自动满 任意选择参考点:其它结点与参考点的电压差即 足的说明 是结点电压(位),方向为从独立结点指向参考结点。 UA-UB (Ux-uB)+uB-us=O KVL自动满足
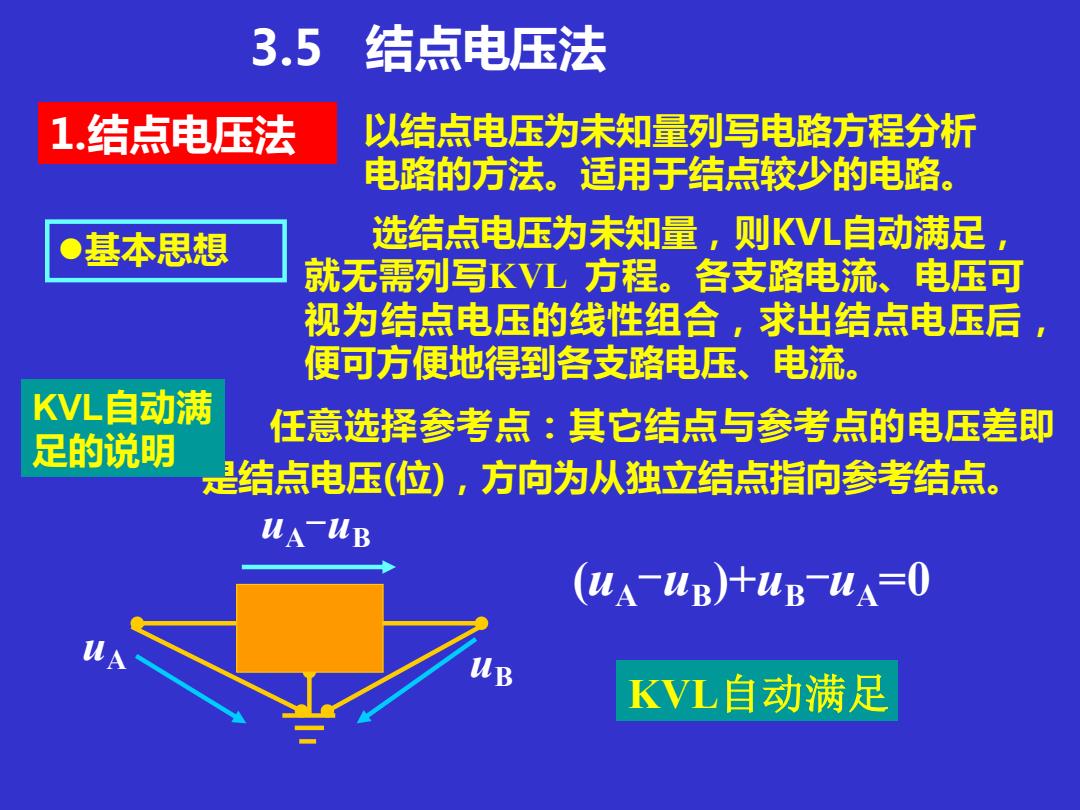
3.5 结点电压法 选结点电压为未知量,则KVL自动满足, 就无需列写KVL 方程。各支路电流、电压可 视为结点电压的线性组合,求出结点电压后, 便可方便地得到各支路电压、电流。 ⚫基本思想 以结点电压为未知量列写电路方程分析 电路的方法。适用于结点较少的电路。 1.结点电压法 任意选择参考点:其它结点与参考点的电压差即 是结点电压(位),方向为从独立结点指向参考结点。 (uA-uB )+uB-uA=0 KVL自动满足 KVL自动满 足的说明 uA-uB uA uB
●列写的方程 结点电压法列写的是结点上的KC方 程,独立方程数为: 与支路电流法相比, n-1) 方程数减少b-(m1)个。 2.方程的列写 (1)选定参考结点 R 标明其余n-1个独 is 立结点的电压
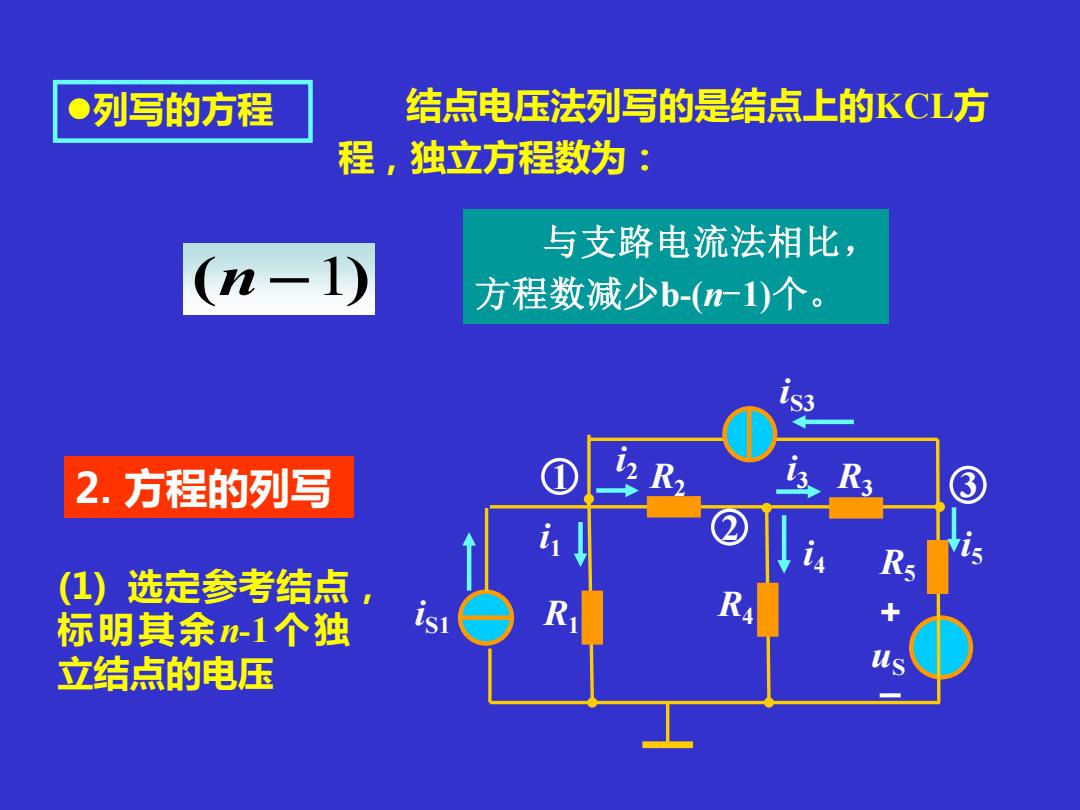
2. 方程的列写 iS1 uS iS3 R1 i1 i2 i3 i4 i5 R2 R5 R3 R4 + _ (1) 选定参考结点, 标明其余n-1个独 立结点的电压 1 3 2 ⚫列写的方程 结点电压法列写的是结点上的KCL方 程,独立方程数为: 与支路电流法相比, (n −1) 方程数减少b-(n-1)个
(2)列KCL方程: ∑I=0 2R2 itiz-isi+is2 Rs -2+i4+3=0 S1 us -i3ti5=一is2 把支路电流用结点电压表示: 十 n一42=is1+isz R R l2=0 R R RA 42-4s+n二4s=-i2 R R
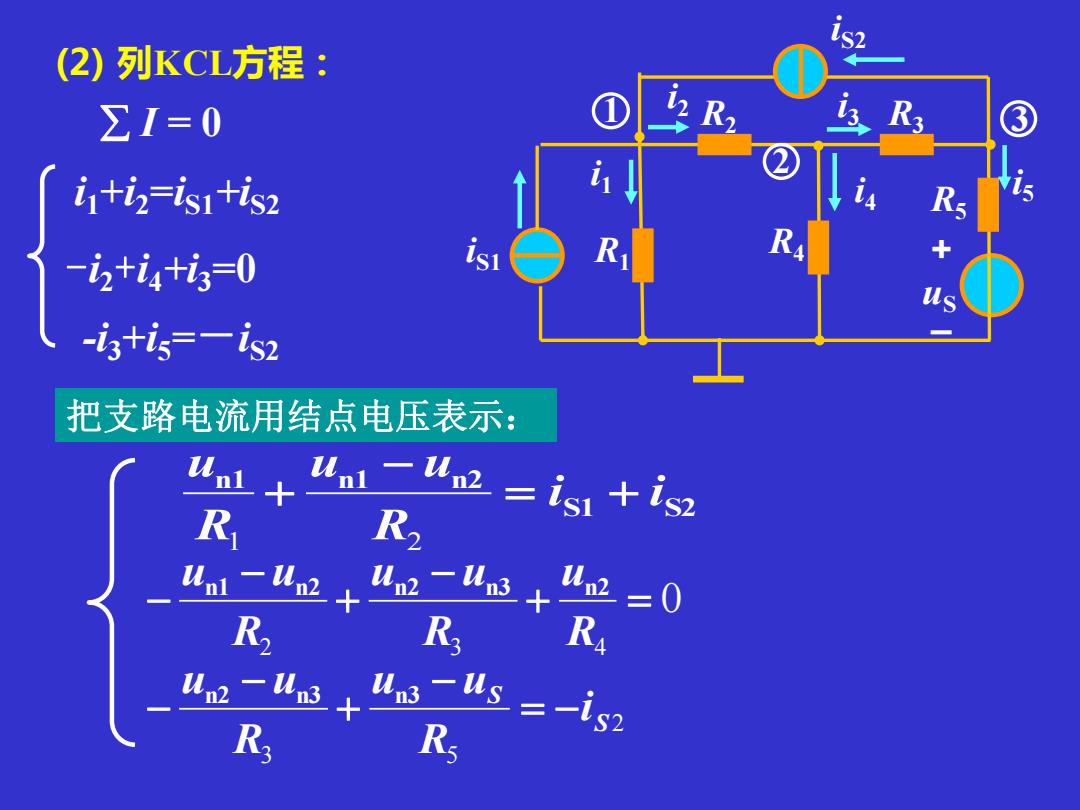
iS1 u S iS2 R 1 i 1 i 2 i3i 4 i 5 R 2 R 5 R 3 R 4 +_ 1 3 2 (2) 列KCL方程: I = 0 i 1 + i2 = iS1+iS2 - i2 + i4+i3=0 把支路电流用结点电压表示: S1 S2 n1 n1 n2 i i R u u Ru = + − + 1 2 0 2 3 4 + = − + − − Ru R u u R un1 un2 n2 n3 n2 - i3 + i5 = - iS2 2 3 5 S S i R u u R u u = − − + − − n2 n3 n3
整理,得: +-(=+ R R R 4ns=0 等效电 )4=-i+ us 流源 R 令G=1/Rk, k=1,2,3,4,5 上式简记为: Gu4n1+G124n2+G134n3=isn1 标准形式的结点 G214n1+G224n2+G234n3=isn2 电压方程 G314n1+G324n2+G334n3=isn3
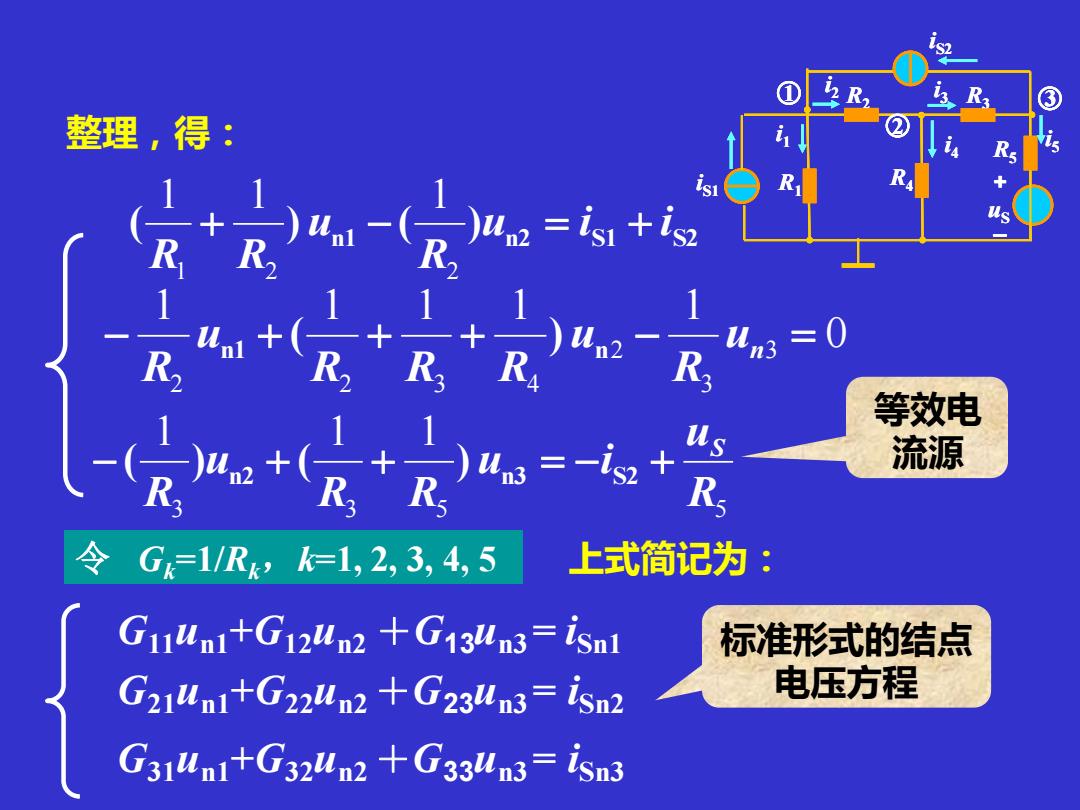
整理,得: n1 n2 S1 S2 ( ) ( )u i i R u R R + − = + 1 2 2 1 1 1 0 1 1 1 1 1 3 3 2 2 2 3 4 − + + + − un = R u R R R u R n1 n ( ) 令 Gk=1/Rk,k=1, 2, 3, 4, 5 上式简记为: G11un1+G12un2 +G13un3= iSn1 3 3 5 5 1 1 1 R u u i R R u R S − ( ) n2 + ( + ) n3 = − S2 + G21un1+G22un2 +G23un3= iSn2 G31un1+G32un2 +G33un3= iSn3 标准形式的结点 电压方程 等效电 流源 iS1 uS iS2 R1 i1 i2 i3 i4 i5 R2 R5 R3 R4 + _ 1 3 2 iS1 uS iS2 R1 i1 i2 i3 i4 i5 R2 R5 R3 R4 + _ iS1 uS iS2 R1 i1 i2 i3 i4 i5 R2 R5 R3 R4 + _ 1 3 2

其中 G11=G+G 结点1的自电导,等于接在结点1上所有 支路的电导之和。 G22=G2+G3+G4 结点2的自电导,等于接在结点2上所有 支路的电导之和。 G33=G3+G5 结点3的自电导,等于接在结点3上所有支 路的电导之和。 G12=G21=- 结点1与结点2之间的互电导,等于接在 结点1与结点2之间的所有支路的电导之 和,为负值。 G23G32=- 结点2与结点3之间的互电导,等于接在结 点1与结点2之间的所有支路的电导之和, 为负值。 自电导总为正,互电导总为负
其 中 G11=G1+G2 结点1的自电导,等于接在结点1上所有 支路的电导之和。 G22=G2+G3+G4 结点2的自电导,等于接在结点2上所有 支路的电导之和。 G12= G21 =-G2 结点1与结点2之间的互电导,等于接在 结点1与结点2之间的所有支路的电导之 和,为负值。 自电导总为正,互电导总为负。 G33=G3+G5 结点3的自电导,等于接在结点3上所有支 路的电导之和。 G23= G32 =-G3 结点2与结点3之间的互电导,等于接在结 点1与结点2之间的所有支路的电导之和, 为负值

isni-isi+is2 流入结点1的电流源电流的代数和。 isn2=-is2 us/Rs 流入结点2的电流源电流的代数和。 流入结点取正号,流出取负号。 由结点电压方程求得各结点电压后即可求得各支路电 压,各支路电流可用结点电压表示: 1一2 R R i =4 R
iSn2=-iS2+uS /R5 流入结点2的电流源电流的代数和。 iSn1=iS1+iS2 流入结点1的电流源电流的代数和。 流入结点取正号,流出取负号。 1 n1 1 R u i = 4 n2 R u i 4 = 3 n2 n3 R u u i − 3 = 2 n1 n2 R u u i − 2 = 5 S R u u i n − = 3 5 由结点电压方程求得各结点电压后即可求得各支路电 压,各支路电流可用结点电压表示:

Gi4n1+G124n2+...+G1,n-14nn-1-isnl 般情况 G214nl+G22Wn2+..+G2,-14m,n-l=isn2 Gn-114n1+Gn-124n2+...+Gn-1,n-14n,n-1-iSn,n-1 其中 G一自电导,等于接在结点上所有支路的电导之和 (包括电压源与电阻串联支路)。总为正。 G=G一互电导,等于接在结点与结点之间的所 支路的电导之和,总为负。 m一流入结点的所有电流源电流的代数和(包括 由电压源与电阻串联支路等效的电流源)。 当电路不含受控源时,系数矩阵为对称阵
一 般 情 况 G11un1+G12un2+…+G1,n-1un,n-1=iSn1 G21un1+G22un2+…+G2,n-1un,n-1=iSn2 …… Gn-1,1un1+Gn-1,2un2+…+Gn-1,n-1un,n-1=iSn,n-1 其中 Gii —自电导,等于接在结点i上所有支路的电导之和 (包括电压源与电阻串联支路)。总为正。 当电路不含受控源时,系数矩阵为对称阵。 iSni — 流入结点i的所有电流源电流的代数和(包括 由电压源与电阻串联支路等效的电流源)。 Gij = Gji—互电导,等于接在结点i与结点j之间的所 支路的电导之和,总为负

结点电压法的一般步骤: (1)选定参考结点,标定-1个独立结点; (2)对-1个独立结点,以结点电压为未知量 列写其KCL方程: (3)求解上述方程,得到-1个结点电压: (4)求各支路电流(用结点电压表示): (5)其它分析
结点电压法的一般步骤: (1) 选定参考结点,标定n-1个独立结点; (2) 对n-1个独立结点,以结点电压为未知量, 列写其KCL方程; (3) 求解上述方程,得到n-1个结点电压; (5) 其它分析。 (4) 求各支路电流(用结点电压表示);

例 试列写电路的节点电压方程。 (G1+G2+GS)U1-GU2-GU3=UsGs -G,U1+(G1+G3+G4)U2-G4U3=0 -GSUJ-GAU2+(G4+Gs+Gs)U3=-UsGs 3.无伴电压源支路的处理 (1)以电压源电流为变量,增 补结点电压与电压源间的关系
试列写电路的节点电压方程。 (G1+G2+GS )U1-G1U2-GsU3=USGS -G1U1+(G1 +G3 + G4 )U2-G4U3 =0 -GSU1-G4U2+(G4+G5+GS )U3 =-USGS 例 3. 无伴电压源支路的处理 (1)以电压源电流为变量,增 补结点电压与电压源间的关系 Us G3 G1 G4 G5 G2 + _ GS 3 1 2 Us G3 G1 G4 G5 G2 + _ 3 1 2
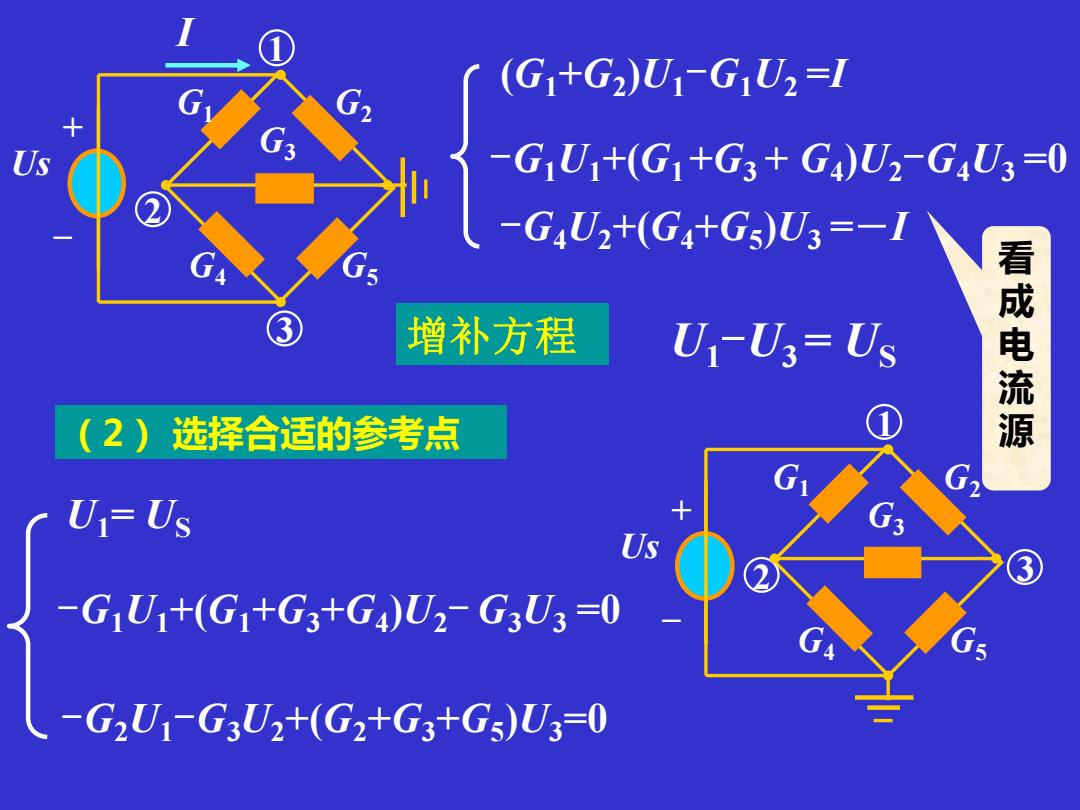
(G1+G2)U1-GU2=1 -G,U1+(G1+G3+G4)U2-G4U3=0 -G4U2+(G4+Gs)U3=-1 增补方程 U-U3=Us 看成电流源 (2)选择合适的参考点 U1=Us -G1U1+(G1+G3+G4)U2-G3U3=0 -G2U1-G3U2+(G2+G3+Gs)U3=0
I (G1+G2 )U1-G1U2 =I -G1U1+(G1 +G3 + G4 )U2-G4U3 =0 -G4U2+(G4+G5 )U3 =-I U1-U3 = US 看 成 电 流 源 增补方程 (2) 选择合适的参考点 U1= US -G1U1+(G1+G3+G4 )U2- G3U3 =0 -G2U1-G3U2+(G2+G3+G5 )U3=0 Us G3 G1 G4 G5 G2 + _ 3 1 2 Us G3 G1 G4 G5 G2 + _ 3 1 2