聊城大学：《电路分析》课程教学资源（PPT课件讲稿）第八章 相量法（2/2）

4.相量法的应用 (1)同频率正弦量的加减 u(t)=V2 U,cos(@t+Y)=Re(V2Urei@) u2(t)=V2U2cos(@t+Ψ，)=Re(V2i2eo u(t)=u(t)+uz(t)=Re(V2Urei@)+Re(V2Uz ei) Re(V2 Urei+V2Uzei@)Re(V2(U1+U2)ei) 可得其相量关系为： U=U+U2 i1土2=3 故同频正弦量相加减运算变 成对应相量的相加减运算。 i1±12=

4. 相量法的应用 (1) 同频率正弦量的加减 故同频正弦量相加减运算变 成对应相量的相加减运算。 i1  i2 = i3 1 2 3 I I I    =  ( ) 2 cos( ) R ( 2 ) ( ) 2 cos( ) R ( 2 ) j 2 2 2 2 j 1 1 1 1 t t u t U t Ψ e U e u t U t Ψ e U e     • • = + = = + = R ( 2 2 ) R ( 2( ) ) ( ) ( ) ( ) R ( 2 ) R ( 2 ) j 1 2 j 2 j 1 j 2 j 1 1 2 t t t t t e U e U e e U U e u t u t u t e U e e U e      • • • • • • = + = + = + = + U  U U1 U2 可得其相量关系为：  =  + 

例4，(0)=6V2c0s(3141+30)y U=6∠30°V 42()=4W2c0s(314t+60°)V 0=01+02=6∠30°+4∠60°=5.19+3+2+j3.46 =7.19+j6.46=9.64∠41.9°V .(t)=41(t)+42(t)=9.64W2c0s(314t+41.9)V 也可借助相量图计算 首尾相接 Im 60 41.9 30 Re 30 Re 60

例 ( ) 4 2cos(314 60 ) V ( ) 6 2cos(314 30 ) V o 2 1 = + = + u t t u t t  也可借助相量图计算 4 60 V 6 30 V o 2 o 1 =  =  U U   ( ) ( ) ( ) 9.64 2cos(314 41.9 ) V o u t = u1 t + u2 t = t +      6 30 4 60 U = U1 +U2 =  +  Re Im  30 U1   41.9 U  Re Im  41.9  30 U1   60U2  U  = 5.19 + j3 + 2 + j3.46 = 7.19 + j6.46 9.64 41.9 V o =   60 U2  首尾相接

2.正弦量的微分，积分运算 i=2Icos(@t+y)<>I=IZW 微分运算： 】 dt =-V2I@sin(@t+V:) =2 to+g+月 告a+同月-ei di →jo1=ow,+3

2 . 正弦量的微分，积分运算 2 cos( ) i i i = I  t +  I  = I 微分运算: 2 →  =  +  i j I I dt di   ( ) ( )i i I t I t dt d dt di      = − + = + 2 sin 2 cos 2         +    i I dt di       = + + 2 2 cos     i I t • = j I

2.正弦量的微分，积分运算 i=V2Icos(ot+w,)<→i=I∠y, 积分运算： ∫d=j27cos(or+y,)d =21sm(or+w,） j曲“ -nmlu*以到

2 . 正弦量的微分，积分运算 2 cos( ) i i i = I  t +  I  = I i t I ( t ) t i d 2 cos d   =  + 积分运算: 2     → = −  i I j I idt  ( )i I t   = 2 sin + 1       = + − 2 2 cos     i t I     j I I idt i •  =        −  2

例 i(t)=J2Icos(@t+y:) u(t) u(t)=Ri+L 用相量运算： U=Ri+joLi+ 相量法的优点： (1)把时域问题变为复数问题； (2)把微积分方程的运算变为复数方程运算； (3)可以把直流电路的分析方法直接用于交流电路；

例 ( ) 2 cos( ) i i t = I  t + 1 ( )  = + + idt dt C di u t Ri L R i(t) u(t) L + - C 用相量运算： j C I U RI j LI     =  +  + 相量法的优点： （1）把时域问题变为复数问题； （2）把微积分方程的运算变为复数方程运算； （3）可以把直流电路的分析方法直接用于交流电路；

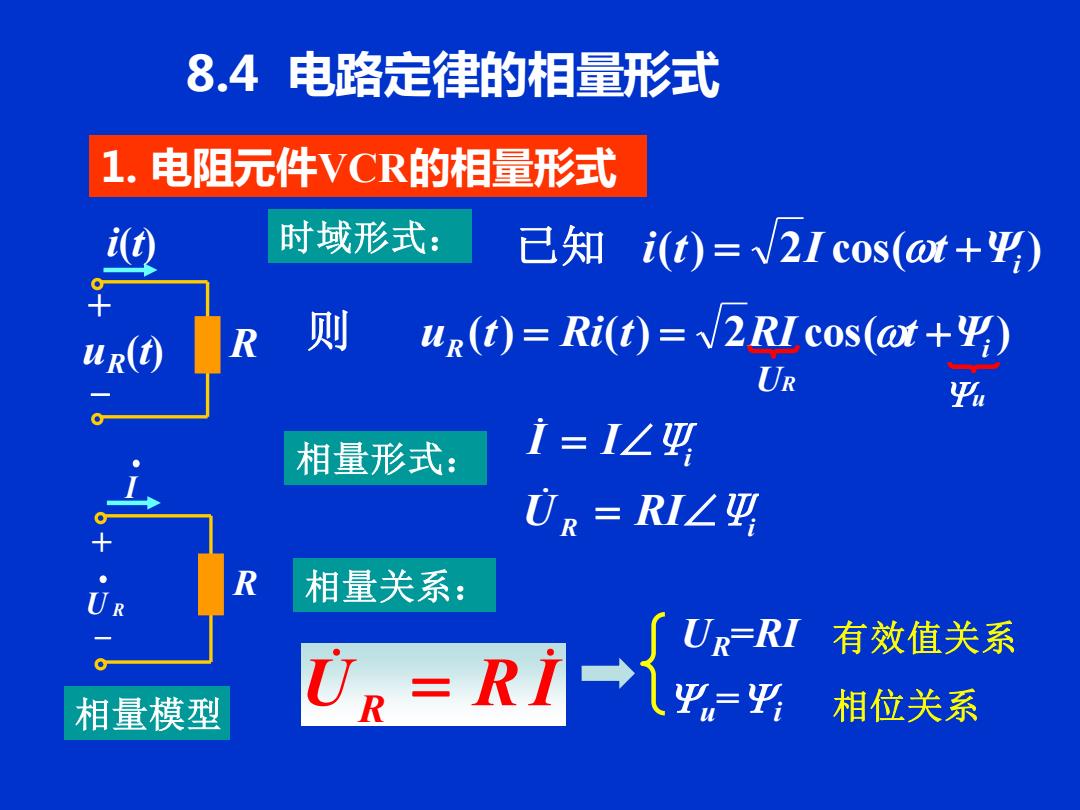
8.4电路定律的相量形式 1.电阻元件VCR的相量形式 i(t 时域形式： 已知i(t)=V2Icos(@t+平) R 则 ur(t)=Ri(t)=V2RIcos(at+) UR a 相量形式： 1=I∠巧 UR=RI∠玛 R 相量关系： G=R-{ UR-RI 有效值关系 相量模型 相位关系

8.4 电路定律的相量形式 1. 电阻元件VCR的相量形式 时域形式： 相量形式： R i i U RI Ψ I I Ψ =  =    相量模型 ( ) 2 cos( ) Ψi 已知 i t = I t + ( ) ( ) 2 cos( ) R Ψi 则 u t = Ri t = RI t + uR(t) i(t) R + - 有效值关系 相位关系 R + - U R • • I UR u 相量关系： U RI R  =  UR=RI u =i

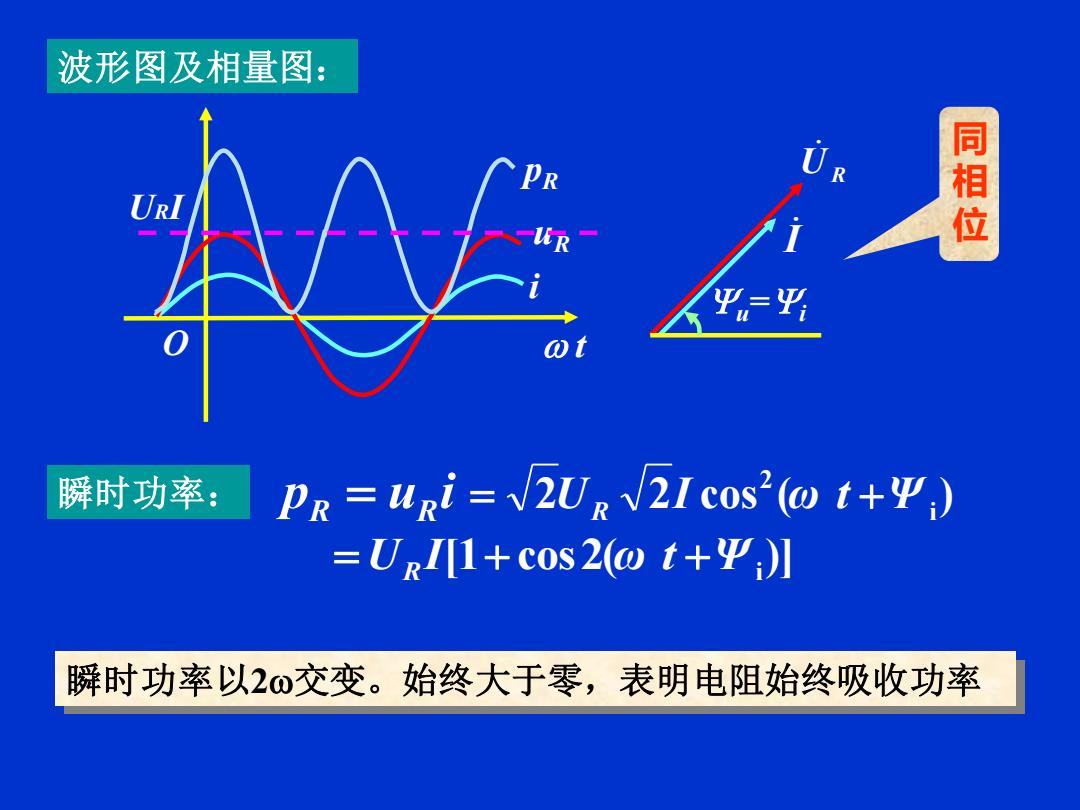
波形图及相量图： 同相位 01 瞬时功率： 卫R=uri=V2URV2Icos2(ot+Ψ) =URII1+c0s2(ot+Ψ；] 瞬时功率以2o交变。始终大于零，表明电阻始终吸收功率

瞬时功率： p u i R = R 波形图及相量图： i O  t uR pR UR  I  u =i URI 瞬时功率以2交变。始终大于零，表明电阻始终吸收功率 2 2 cos ( )i 2 = UR I ω t +Ψ [1 cos2( )] Ψi U I ω t = R + + 同 相 位

2.电感元件VCR的相量形式 时域形式： 已知i(t)=√2Ic0s(ot+4:) 则 u()=Ldi=-VZoLIsin1+) dt =20LIs®t+g+号) 相量形式： i=I∠平 U2=oL1∠，+π/2)→U2=joLi @I 相量关系： Uz=joL1=议1 有效值关系：U=oLI 相量模型 相位关系：平=平+90°

时域形式： i(t) uL (t) L + - 相量形式： ( ) 2 cos( ) ψi 已知 i t = I  t + ) 2 2 cos( 2 sin( ) d d ( ) ( ) π = + + = = − + i L i L I t Ψ L I t Ψ t i t u t L   则   相量模型 j L + - U L • • I 相量关系： U j LI jX I L L  =   =  有效值关系：U= L I 相位关系：u =i +90° 2. 电感元件VCR的相量形式 U LI (Ψ ) U j LI I I Ψ L i L i     =  +  =  =  2

感抗和感纳： X=oL=2元亿，称为感抗，单位为2欧姆) B=1/oL=1/2πL,感纳，单位为S 感抗的物理意义： (1)表示限制电流的能力： (2)感抗和频率成正比； XL o=0(直流)，X,=0,短路； 0→0，X→o0,开路； U=jXii=joLi, 相量表达式：

感抗的物理意义： (1) 表示限制电流的能力； (2) 感抗和频率成正比；  XL 相量表达式: XL= L=2fL，称为感抗，单位为 (欧姆) BL=1/ L =1/2fL， 感纳，单位为 S 感抗和感纳: U jX I j LI , L  =  =   , , ; 0( ), 0, ; 开 路 直 流 短 路  →  →   = = L L X X U j L U L I jB U j L      =  − = = 1 1

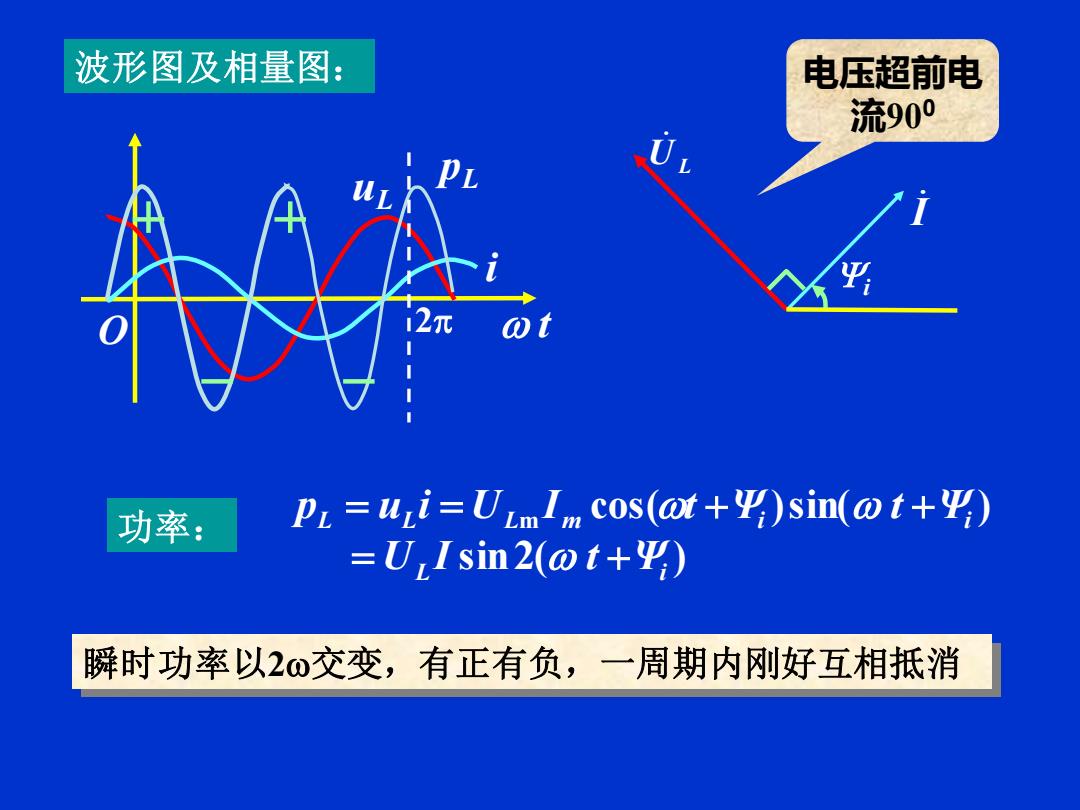
波形图及相量图： 电压超前电 流900 功率： PL =uLi=ULmIm cos(@t+)sin(@t+y) =UIsin2(ot+平) 瞬时功率以2ω交变，有正有负，一周期内刚好互相抵消

功率： sin2( ) cos( )sin( ) m L i L L L m i i U I t Ψ p u i U I t Ψ t Ψ = + = = + +     t i O uL pL 2 瞬时功率以2交变，有正有负，一周期内刚好互相抵消 UL  I  i 波形图及相量图： 电压超前电 流900