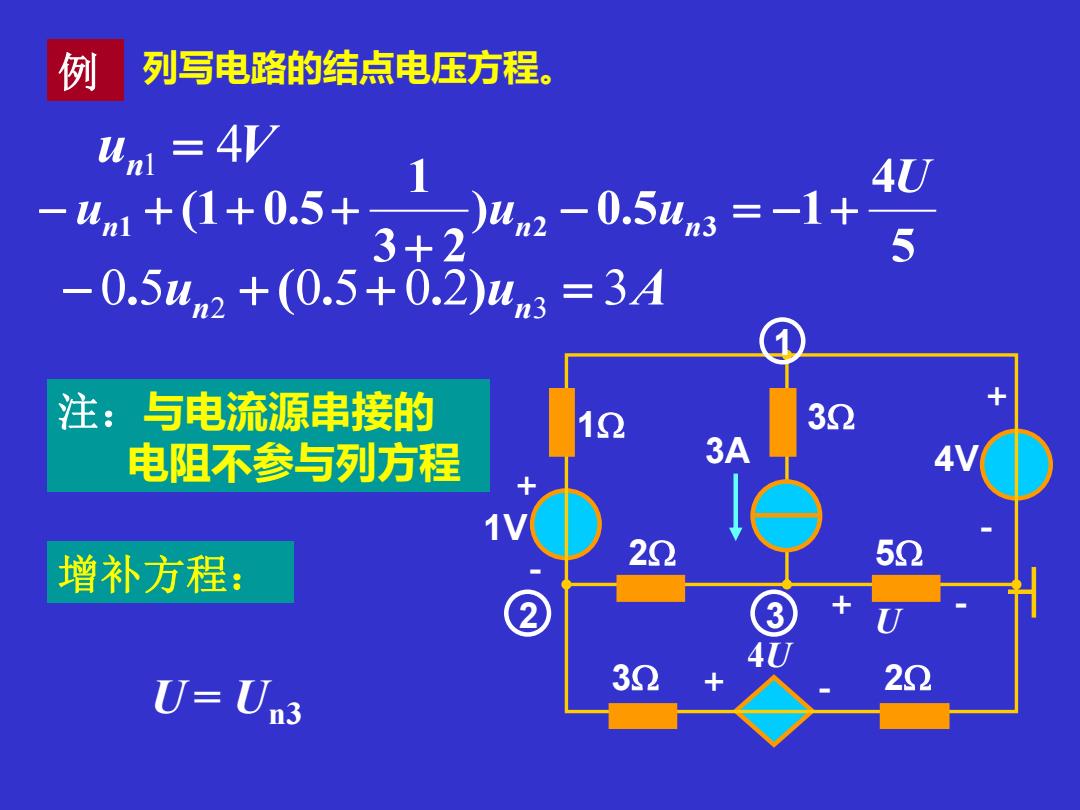
例 列写电路的结点电压方程。 um 41 -4n1+(1+0.5+ 37a-0543= 4U 5 -0.54n2+(0.5+0.2)wn3=3A 注:与电流源串接的 12 32 电阻不参与列方程 3A 增补方程: 20 52 U=Un3 32 20
例 列写电路的结点电压方程。 1V + + + + - - - - 3 2 2 1 5 3 4V U 4U 3A 3 1 2 un1 = 4V 5 4 ) 0.5 1 3 2 1 1 (1 0.5 2 3 U un un − un = − + + − + + + − 0.5un2 + (0.5+ 0.2)un3 = 3A 注:与电流源串接的 电阻不参与列方程 增补方程: U = Un3
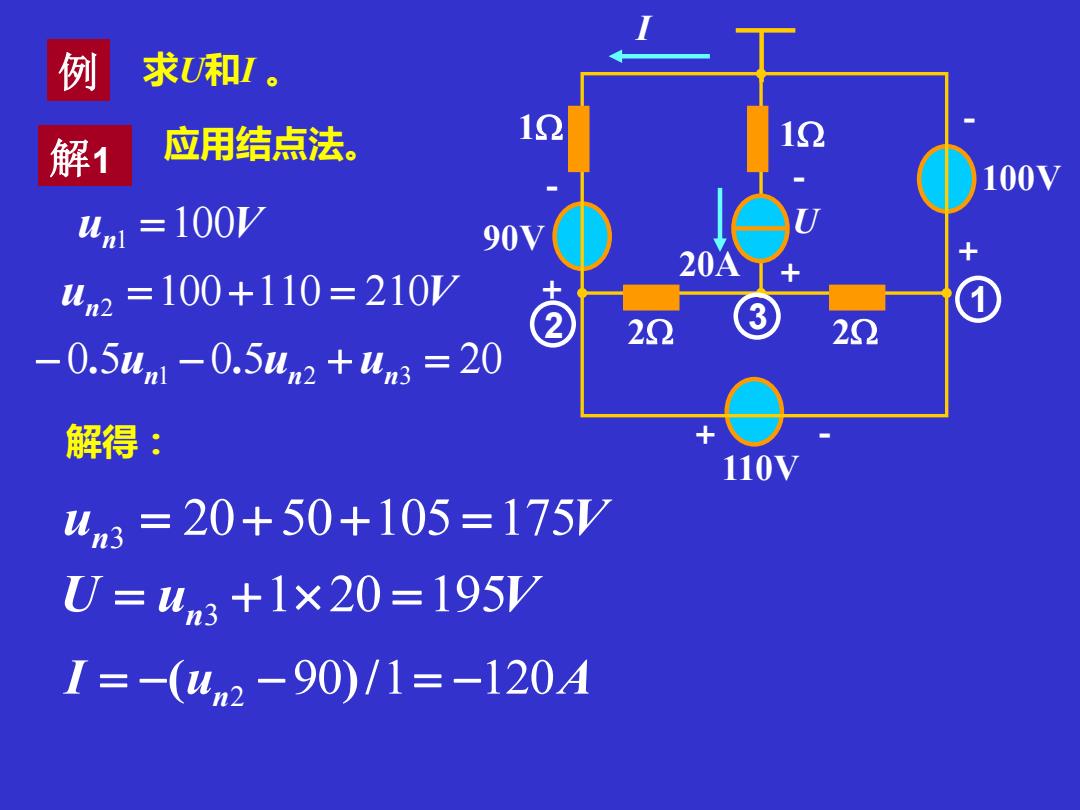
例 求U和I。 解1 应用结点法。 12 100V um =100V 90V 20A um2=100+110=210W 20 3 20 -0.54n1-0.54n2+4m3=20 解得: 110V 4m3=20+50+105=175/ U=4n3+1×20=195/ I=-(4m2-90)/1=-120A
例 求U和I 。 90V + + + - - - 2 1 2 1 100V 20A 110V + - U I 解1 应用结点法。 3 1 2 un1 =100V un2 =100+110 = 210V − 0.5un1 − 0.5un2 + un3 = 20 un3 = 20+ 50+105 =175V U = un3 +120 =195V I = −(un2 − 90)/1= −120A 解得:
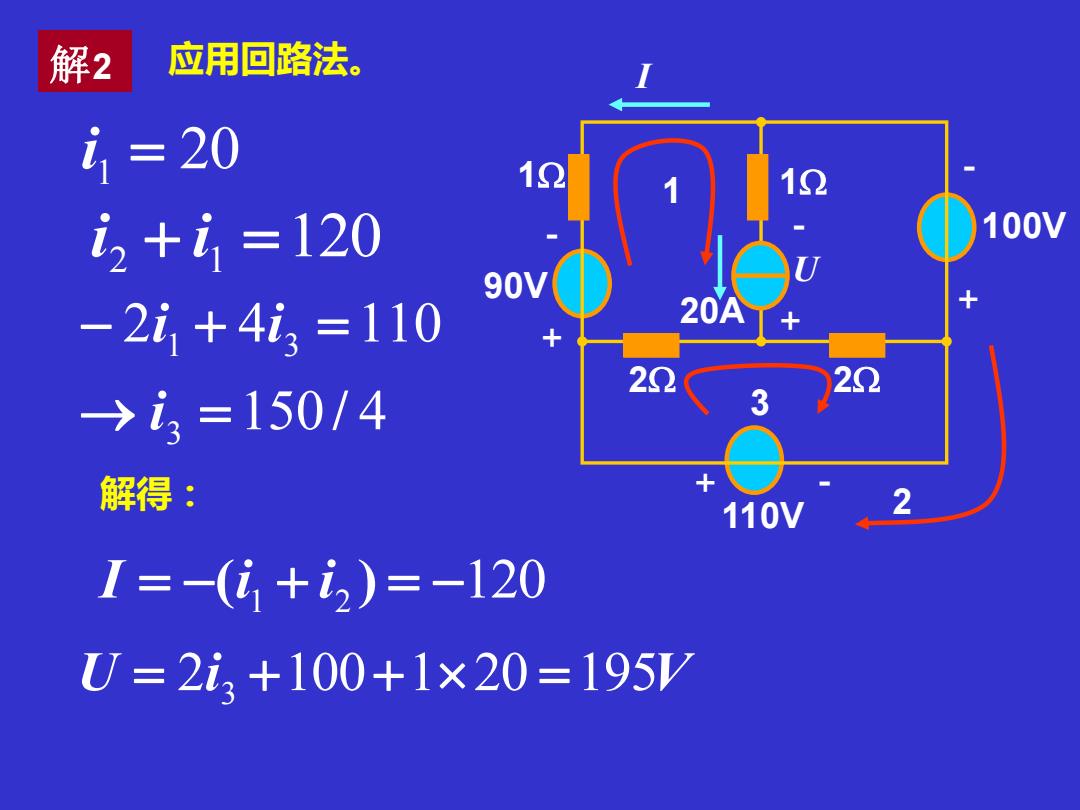
解2 应用回路法。 1=20 i2+i=120 100V 90V -2i,+4i3=110 20A 20 →i3=150/4 、3 解得: 110V 2 I=-(i+2)=-120 U=2i3+100+1×20=195W
90V + + + - - - 2 1 2 1 100V 20A 110V + - U 解2 应用回路法。 I 1 2 3 i 1 = 20 i 2 + i 1 =120 150 4 2 4 110 3 1 3 → = / − + = i i i I = −(i 1 + i 2 ) = −120 U = 2i 3 +100+120 =195V 解得:

第三章小结 掌握电路方程的列写方法: 支路电流法 回路电流法 节点电压法
第三章 小结 掌握电路方程的列写方法: 支路电流法 回路电流法 节点电压法

●树(Tree)→ T是连通图的一个子图满足下列条件: (1)连通 (2)包含所有节点 (3)不含闭合路径 基本回路(单连支回路):基本回路具有独占的一条连枝 n个结点的电路,独立的KCL方程为n-1个。 KV的独立方程数-基本回路数=b-(n-1)
⚫ 树 (Tree) T是连通图的一个子图满足下列条件: (1)连通 (2)包含所有节点 (3)不含闭合路径 基本回路(单连支回路):基本回路具有独占的一条连枝 n个结点的电路, 独立的KCL方程为n-1个。 KVL的独立方程数=基本回路数=b-(n-1)

支路电流法的一般步骤: (1)标定各支路电流的参考方向: (2)选定(n-1)个节点,列写其KC方程; (3)选定b(n-1)个独立回路,列写其KVL方程: (元件特性代入) (4)求解上述方程,得到b个支路电流; (5)进一步计算支路电压和进行其它分析
支路电流法的一般步骤: (1) 标定各支路电流的参考方向; (2) 选定(n–1)个节点,列写其KCL方程; (3) 选定b–(n–1)个独立回路,列写其KVL方程; (元件特性代入) (4) 求解上述方程,得到b个支路电流; (5) 进一步计算支路电压和进行其它分析
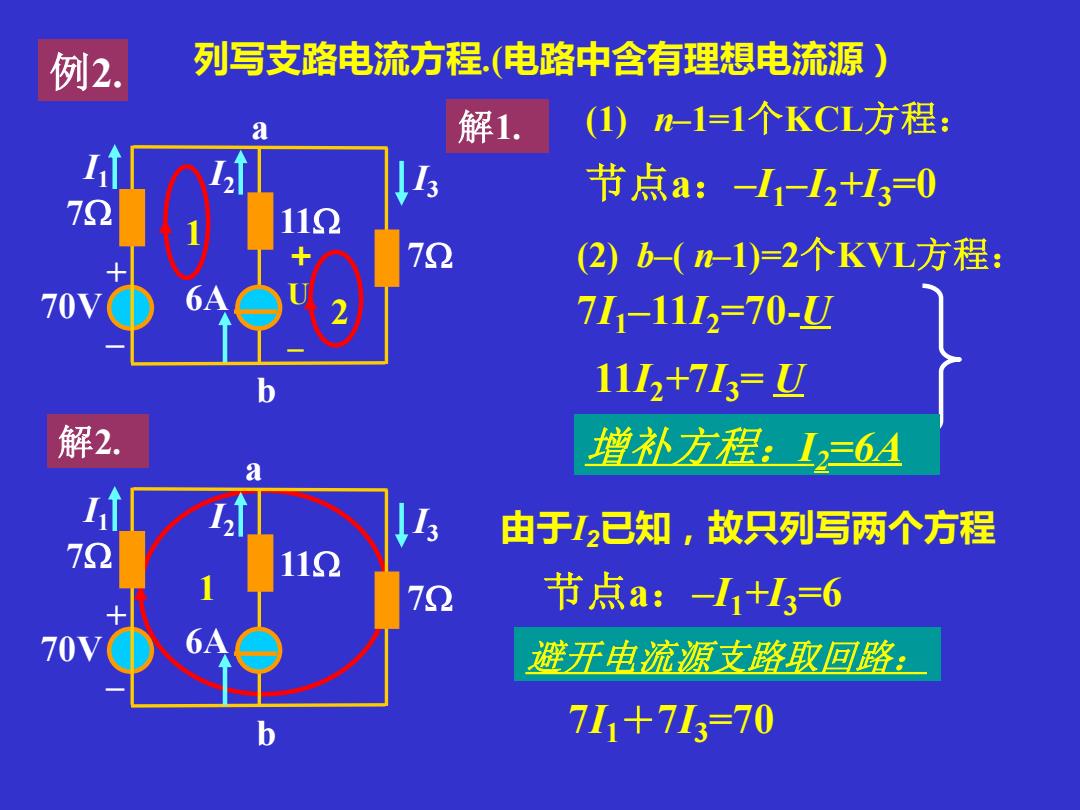
例2. 列写支路电流方程.(电路中含有理想电流源 a 解1. (1)n-1=1个KCL方程: 节点a:-I1-I2+I3=0 70 (2)b-(m-1)=2个KVL方程: 711-1112=70-☑ 1112+713=☑ 解2. 增款方程:I三6A a 由于12已知,故只列写两个方程 112 72 节点a:-11+13=6 避开电流源支路取回路: 711+7I3=70
例2. 节点a:–I1–I2+I3=0 (1) n–1=1个KCL方程: 列写支路电流方程.(电路中含有理想电流源) 解1. (2) b–( n–1)=2个KVL方程: 11I2+7I3= U 7I1–11I2=70-U a 1 70V 2 6A 7 b + – I1 I3 I2 7 11 增补方程:I2=6A + U _ 1 解2. 70V 6A 7 b + – I1 I3 I2 7 11 a 由于I2已知,故只列写两个方程 节点a:–I1+I3=6 避开电流源支路取回路: 7I1+7I3=70

例3. 列写支路电流方程.电路中含有受控源 a 解 节点a:-I1-2+L3=0 711-1112=70-5U 72 1112+713=5U 70 增补方程:=73 有受控源的电路,方程列写分两步: (1)先将受控源看作独立源列方程; (2)将控制量用未知量表示,并代入(1)中所列的方 程,消去中间变量
例3. 节点a:–I1–I2+I3=0 列写支路电流方程.(电路中含有受控源) 解 11I2+7I3= 5U 7I1–11I2=70-5U 增补方程:U=7I3 a 1 70V 2 7 b + – I1 I3 I2 7 11 + 5U _ + U _ 有受控源的电路,方程列写分两步: (1) 先将受控源看作独立源列方程; (2) 将控制量用未知量表示,并代入(1)中所列的方 程,消去中间变量

3.4 回路电流法 (loop current method) 1.回路电流法 以基本回路中的回路电流为未知量 列写电路方程分析电路的方法。当 取网孔电流为未知量时,称网孔法 ●基本思想 为减少未知量(方程)的个数,假想每个回路中 有一个回路电流。各支路电流可用回路电流的 线性组合表示。来求得电路的解。 需要列写的方程 回路电流在独立回路中是闭合的,对每个相关节点均流进一 次,流出一次,所以KCL自动满足。因此回路电流法是对独立回 路列写KVL方程,方程数为 与支路电流法相比 b-(n-1) 方程数减少-1个
3.4 回路电流法 (loop current method) ⚫基本思想 为减少未知量(方程)的个数,假想每个回路中 有一个回路电流。各支路电流可用回路电流的 线性组合表示。来求得电路的解。 1.回路电流法 以基本回路中的回路电流为未知量 列写电路方程分析电路的方法。当 取网孔电流为未知量时,称网孔法 回路电流在独立回路中是闭合的,对每个相关节点均流进一 次,流出一次,所以KCL自动满足。因此回路电流法是对独立回 路列写KVL方程,方程数为: ⚫需要列写的方程 与支路电流法相比, b − (n −1) 方程数减少n-1个

对于具有=b-(n-1)个回路的电路,有: Ruin+Rin+...+Ruiuusu R21n+R222+.…+R2rFus2 Rnin+Rpin+...+Ruiu-usu 其中: Rk:自电阻(为正) +:流过互阻的两个回路电流方向相同 R:互电阻 一:流过互阻的两个回路电流方向相反 0:无关
对于具有 l=b-(n-1) 个回路的电路,有: 其中: Rjk:互电阻 + : 流过互阻的两个回路电流方向相同 - : 流过互阻的两个回路电流方向相反 0 : 无关 R11i l1+R12i l2+ …+R1l i ll=uSl1 … R21i l1+R22i l2+ …+R2l i ll=uSl2 Rl1 i l1+Rl2 i l2+ …+Rll i ll=uSll Rkk:自电阻(为正)