
4.3戴维宁定理和诺顿定理 (Thevenin-Norton Theorem) 工程实际中,常常碰到只需研究某一支路的电 压、电流或功率的问题。; 对所研究的支路来说,电 路的其余部分就成为一个有源二端网络,可等效变 换为较简单的含源支路(电压源与电阻串联或电流 源与电阻并联支路),使分析和计算简化。 戴维宁定 理和诺顿定理正是给出了等效含源支路及其计算方 法
4.3 戴维宁定理和诺顿定理 (Thevenin-Norton Theorem) 工程实际中,常常碰到只需研究某一支路的电 压、电流或功率的问题。对所研究的支路来说,电 路的其余部分就成为一个有源二端网络,可等效变 换为较简单的含源支路(电压源与电阻串联或电流 源与电阻并联支路), 使分析和计算简化。戴维宁定 理和诺顿定理正是给出了等效含源支路及其计算方 法
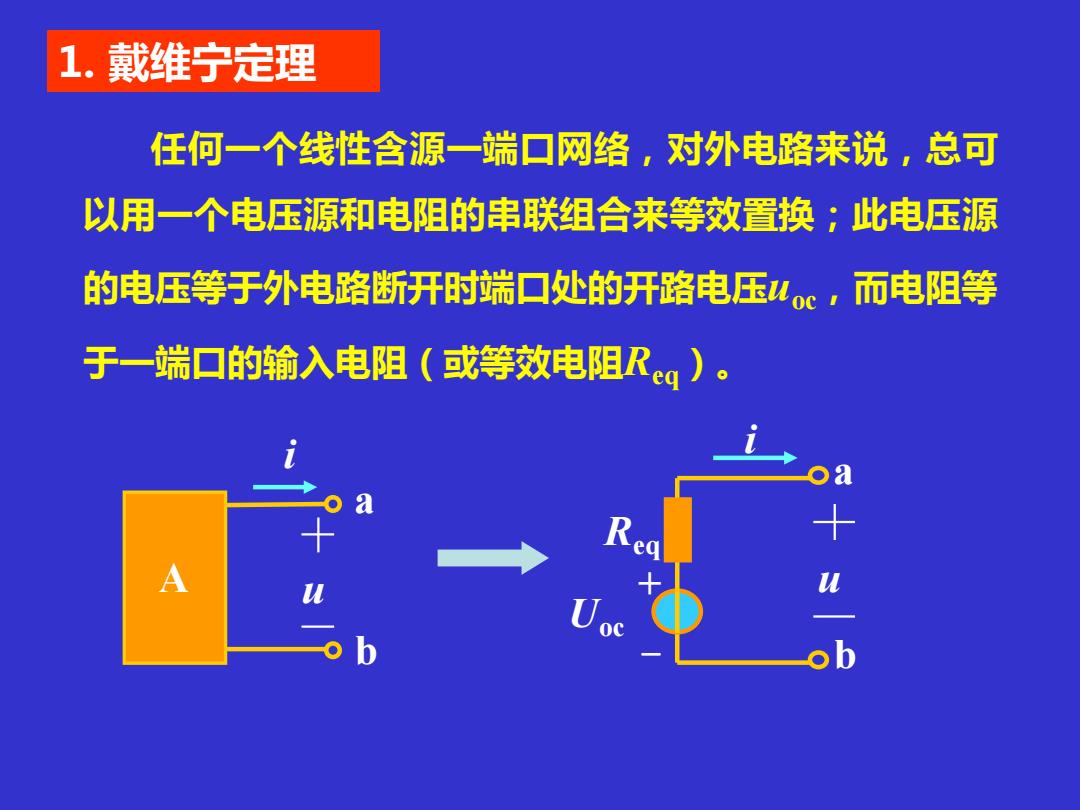
1.戴维宁定理 任何一个线性含源一端口网络,对外电路来说,总可 以用一个电压源和电阻的串联组合来等效置换;此电压源 的电压等于外电路断开时端口处的开路电压4oc,而电阻等 于一端口的输入电阻(或等效电阻Reg)。 ob
1. 戴维宁定理 任何一个线性含源一端口网络,对外电路来说,总可 以用一个电压源和电阻的串联组合来等效置换;此电压源 的电压等于外电路断开时端口处的开路电压uoc,而电阻等 于一端口的输入电阻(或等效电阻Req)。 A a b i u i a b Req Uoc + - u
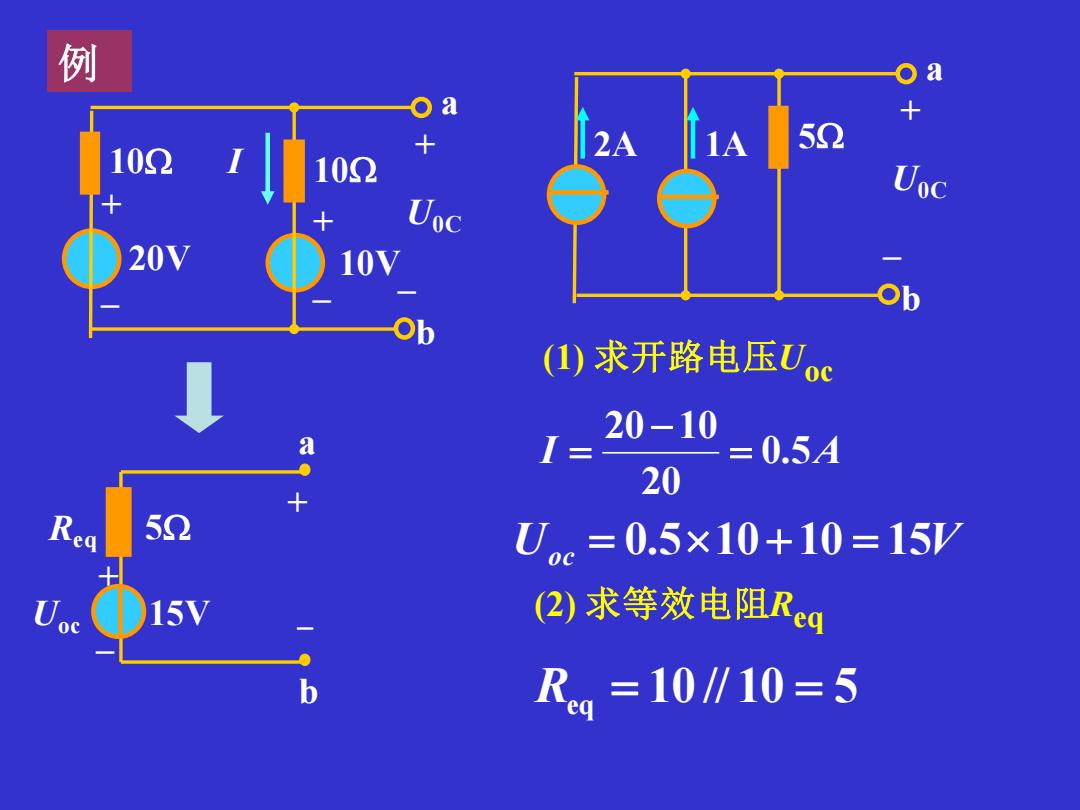
例 52 100 2A 1A 102 Uoc Uoc 20V 10V ob ob (1)求开路电压Uoc 20-10 a I= =0.5A 20 Rea 52 Uc=0.5×10+10=15Y Uoc 15V (2)求等效电阻Rg b Rg=10/10=5
I 例 Uoc a b + – Req 5 15V - + (1) 求开路电压Uoc (2) 求等效电阻Req 10 10 + – 20V + – U0C a b + – 10V 2A 1A 5 + – U0C a b I 0.5A 20 20 10 = − = 10 // 10 5 Req = = Uoc = 0.510+10 = 15V
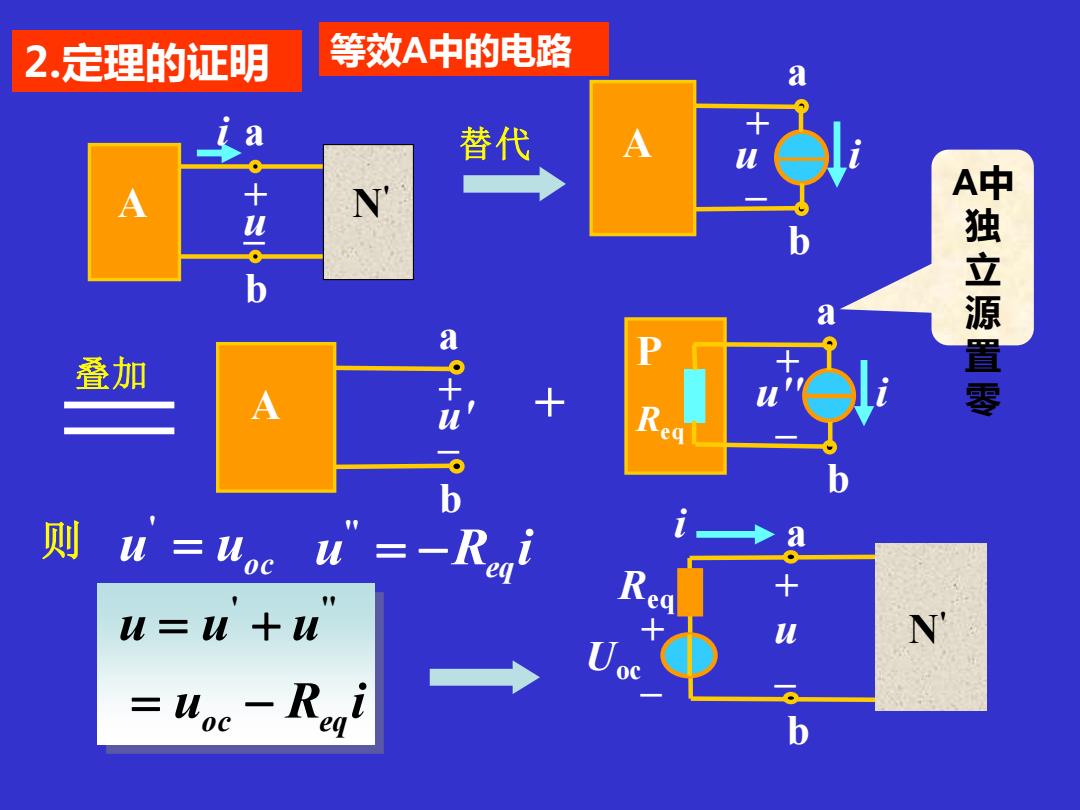
2.定理的证明 等效A中的电路 替代 +31 N 叠加 9+3 198 中独立源置零 + u une u"=-Rai 则 R u=u+u N =Hoc-Rogi
2.定理的证明 + a b A i + – u N' i Uoc + – u N' a b + – Req a b A i + – u a b A + – u' a b P i + – u'' Req 则 替代 叠加 A中 独 立 源 置 零 u = uoc ' u R i = − eq '' u R i u u u = oc − eq = + ' '' 等效A中的电路

3.定理的应用 (1)开路电压U的计算 戴维宁等效电路中电压源电压等于将外电路断开时的开 路电压Vc,电压源方向与所求开路电压方向有关。计算 U的方法视电路形式选择前面学过的任意方法,使易于计 算。 等效电阻的计算 等效电阻为将一端口网络内部独立电源全部置零(电压源 短路,电流源开路)后,所得无源一端口网络的输入电阻。 常用下列方法计算:
3.定理的应用 (1) 开路电压Uoc的计算 等效电阻为将一端口网络内部独立电源全部置零(电压源 短路,电流源开路)后,所得无源一端口网络的输入电阻。 常用下列方法计算: (2)等效电阻的计算 戴维宁等效电路中电压源电压等于将外电路断开时的开 路电压Uoc,电压源方向与所求开路电压方向有关。计算 Uoc的方法视电路形式选择前面学过的任意方法,使易于计 算
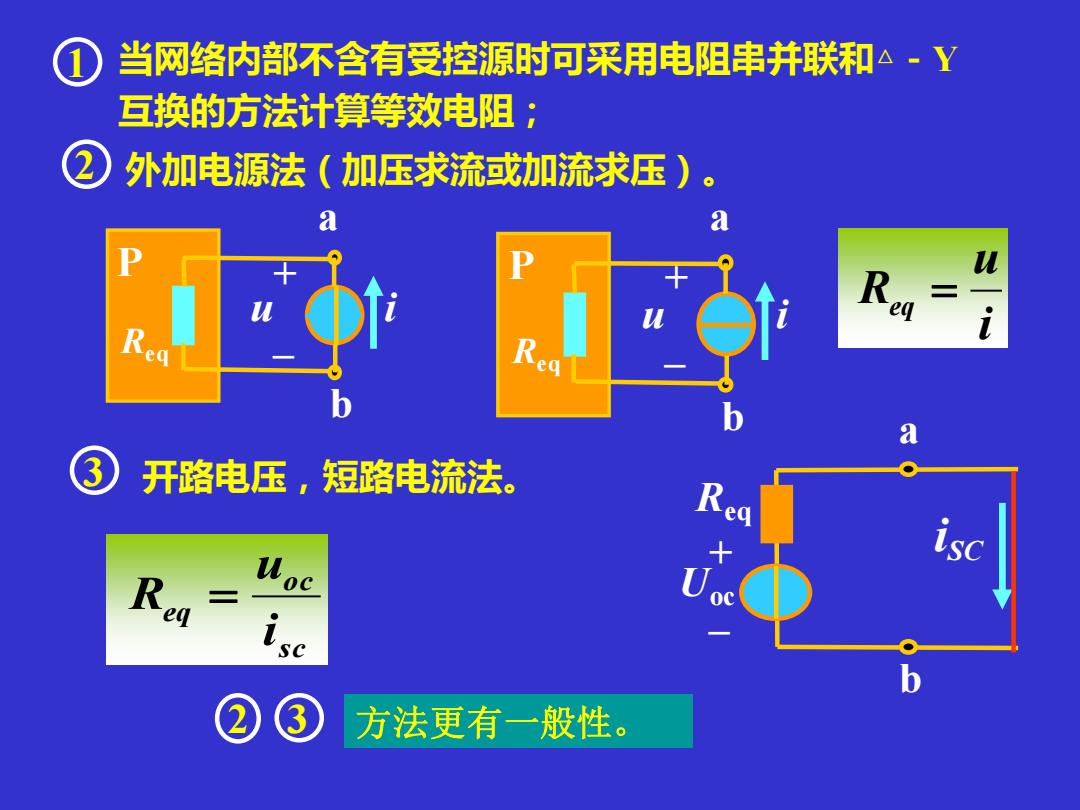
当网络内部不含有受控源时可采用电阻串并联和△-Y 互换的方法计算等效电阻; 外加电源法(加压求流或加流求压) a a 开路电压,短路电流法。 ● sc 方法更有一般性
2 3 方法更有一般性。 当网络内部不含有受控源时可采用电阻串并联和△-Y 互换的方法计算等效电阻; 1 3 开路电压,短路电流法。 2 外加电源法(加压求流或加流求压)。 a b P i + – u Req a b P i + – u Req i u Req = iSC Uoc a b + – Req sc oc eq i u R =
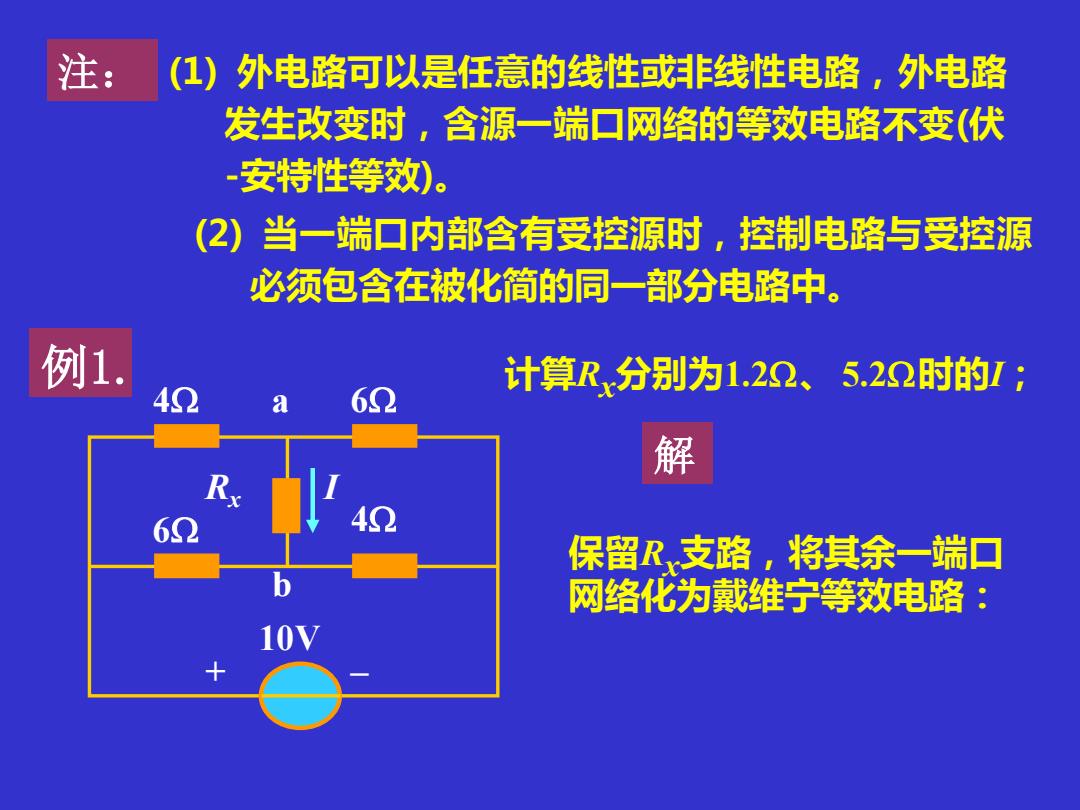
注: (1)外电路可以是任意的线性或非线性电路,外电路 发生改变时,含源一端口网络的等效电路不变(伏 安特性等效)。 (2)当一端口内部含有受控源时,控制电路与受控源 必须包含在被化简的同一部分电路中。 例1. 计算R分别为1.22、5.22时的1; 4Ω a 62 解 62 保留R支路,将其余一端口 网络化为戴维宁等效电路:
(1) 外电路可以是任意的线性或非线性电路,外电路 发生改变时,含源一端口网络的等效电路不变(伏 -安特性等效)。 (2) 当一端口内部含有受控源时,控制电路与受控源 必须包含在被化简的同一部分电路中。 注: 例1. 计算Rx分别为1.2、 5.2时的I; R I x a b + – 10V 4 6 6 4 解 保留Rx支路,将其余一端口 网络化为戴维宁等效电路:
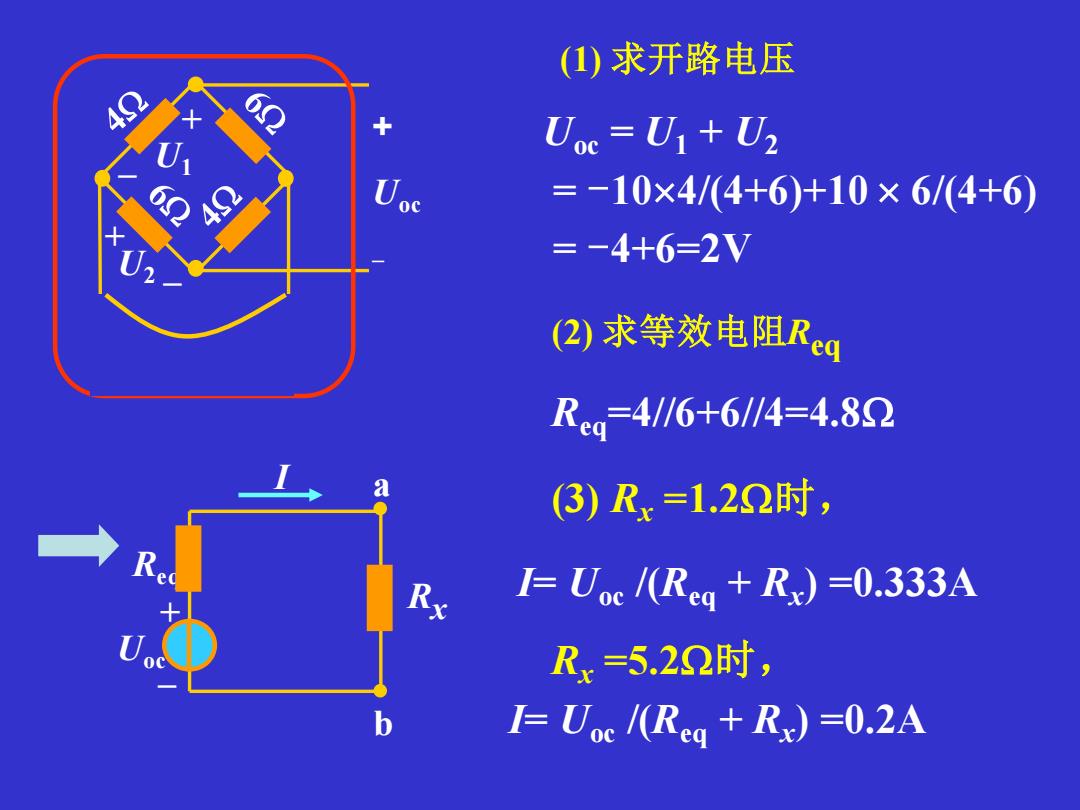
(1)求开路电压 42 6 Uoc=U1+U2 0 oc =-10×4/(4+6)+10×6/(4+6) =-4+6=2V (2)求等效电阻Rq Reg=4/6+6/4=4.82 3)Rx=1.22时, I=Uoc/(Reg +Rx)=0.333A Rx=5.22时, b F Uoc /(Reg +Rx)=0.2A
a b + – 10V – + U2 + – U1 R I x I a b Uoc + – Rx Req (1) 求开路电压 Uoc = U1 + U2 = -104/(4+6)+10 6/(4+6) = -4+6=2V + Uoc _ (2) 求等效电阻Req Req=4//6+6//4=4.8 (3) Rx =1.2时, I= Uoc /(Req + Rx ) =0.333A Rx =5.2时, I= Uoc /(Req + Rx ) =0.2A
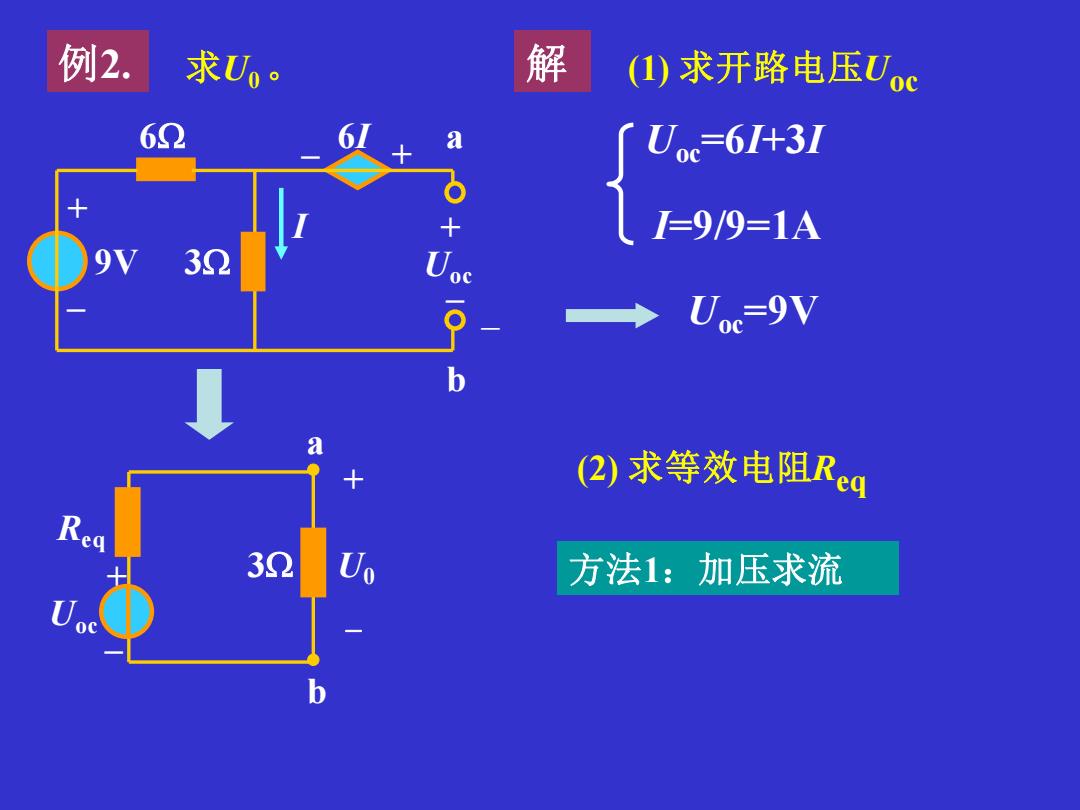
例2. 求Uo。 解 (1)求开路电压Uoc 62 [Ue=61+3/ I=9/9=1A 32 ◆Uc=9V b (2)求等效电阻Rg 32 方法1:加压求流
求U0 。 3 3 6 I + – 9V + – U0 a b – + 6I 例2. Uoc a b + – Req 3 U0 - + 解 (1) 求开路电压Uoc Uoc=6I+3I I=9/9=1A Uoc=9V + – Uoc (2) 求等效电阻Req 方法1:加压求流
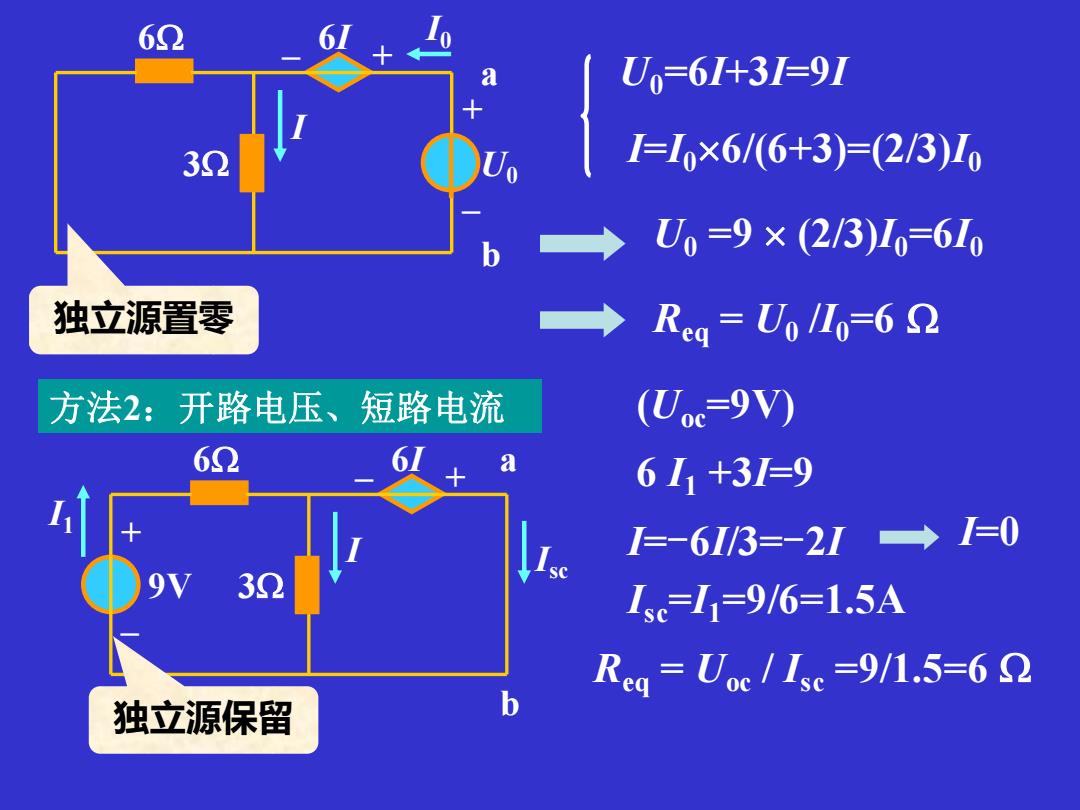
632 U=61+3=91 32 1=I×6/6+3)=(23)0 U=9×(2/3)10=610 独立源置零 Rg=U010=62 方法2:开路电压、短路电流 (Uoc=9V) 62 613+3=9 =-61/3=-21→ I=0 32 sc 1sc=11=9/6=1.5A Rg=Uc/1e=9/1.5=62 独立源保留 b
U0=6I+3I=9I I=I06/(6+3)=(2/3)I0 U0 =9 (2/3)I0=6I0 Req = U0 /I0=6 3 6 I + – U0 a b – + 6I I0 方法2:开路电压、短路电流 (Uoc=9V) 6 I1 +3I=9 I=-6I/3=-2I I=0 Isc =I1=9/6=1.5A Req = Uoc / Isc =9/1.5=6 3 6 I + – 9V Isc a b – + 6I I1 独立源置零 独立源保留