
(4)换路定律 [qe(0)=9e(0) 换路瞬间,若电容电流保持为有限值, 4c(0)=uc(0-)则电容电压(电荷)换路前后保持不变。 乎z(0)尸必z(0-) 换路瞬间,若电感电压保持为有限值, iz(0*)=iz(0-) 则电感电流(磁链) 换路前后保持不变。 注意: (1)电容电流和电感电压为有限值是换路定律成立的条件。 (2)换路定律反映了能量不能跃变
L (0+ )= L (0-) iL (0+ )= iL (0-) qc (0+ ) = qc (0-) uC (0+ ) = uC (0-) (4)换路定律 (1)电容电流和电感电压为有限值是换路定律成立的条件。 注意: 换路瞬间,若电感电压保持为有限值, 则电感电流(磁链)换路前后保持不变。 换路瞬间,若电容电流保持为有限值, 则电容电压(电荷)换路前后保持不变。 (2)换路定律反映了能量不能跃变
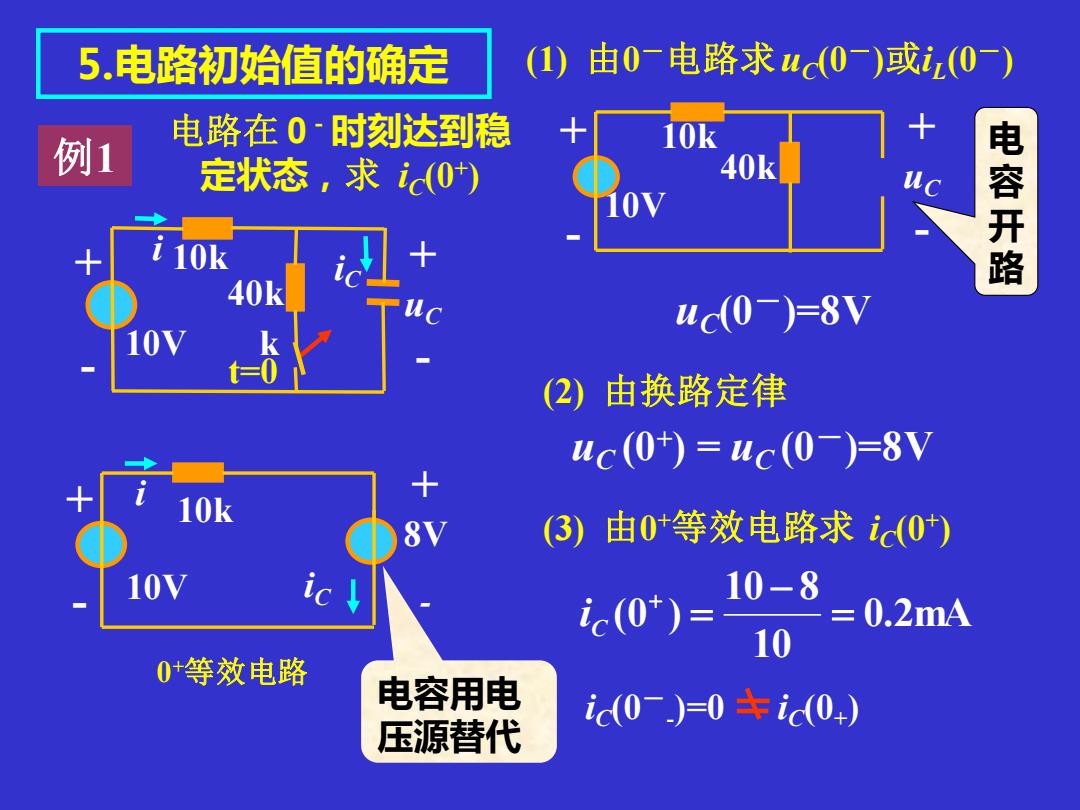
5.电路初始值的确定 (1)由0-电路求4c0)或20) 电路在0时刻达到稳 十 例1 10k 定状态,求i(0*) 40k 电容开路 40k uc(0-=8V 10V t-0 (2) 由换路定律 uc(0)=uc(0-)=8V 10k (3) 由0+等效电路求ic(0*) 10V ic (0*)= 10-8 =0.2m4 10 0+等效电路 电容用电 c(0-)=0主0) 压源替代
5.电路初始值的确定 (2) 由换路定律 uC (0+ ) = uC (0-)=8V + - 10V i iC + 8V - 10k 0 +等效电路 0.2mA 10 10 8 (0 ) = − = + C i (1) 由0-电路求uC(0-)或iL (0-) + - 10V + uC - 10k 40k uC(0-)=8V (3) 由0 +等效电路求 iC(0+ ) iC(0- - )=0 iC(0+ ) 例1 电路在 0-时刻达到稳 定状态,求 iC(0+ ) + - 10V i iC + uC - k 10k 40k 电 容 开 路 电容用电 压源替代 t=0
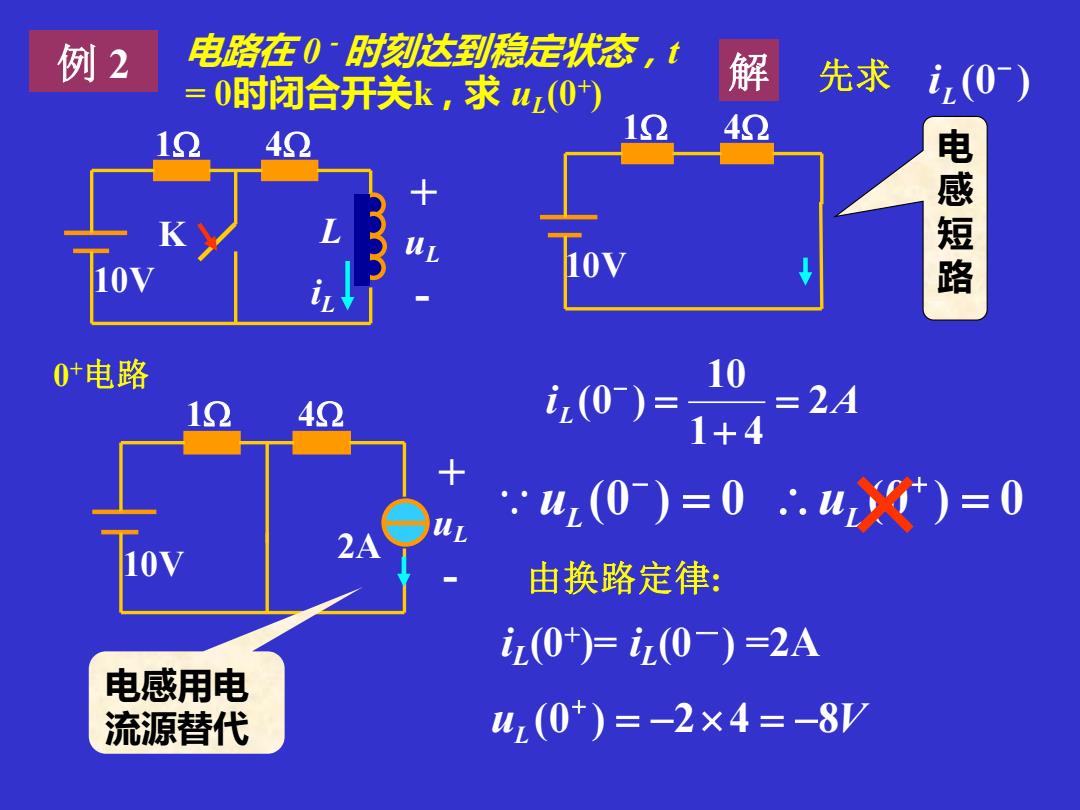
例2 电路在0·时划达到稳定状态,t 0时闭合开关k,求42(0) 解 先求 i,(0) 42 1Ω 42 电感短路 10 0*电路 10 1 42 iz(0)= 1+4 =2A 4(0)=0∴.X)=0 由换路定律: z(0)=z(0-)=2A 电感用电 流源替代 4(0)=-2×4=-8
(0 ) = 0 (0 ) = 0 − + uL uL iL (0+ )= iL (0-) =2A uL (0 ) = −24 = −8V + 例 2 电路在 0-时刻达到稳定状态,t = 0时闭合开关k , 求 uL (0+ ) iL + uL - L 10V K 1 4 + uL - 10V 1 4 0 +电路 2A 先求 i L 2A 1 4 10 (0 ) = + = − 由换路定律: 电感用电 流源替代 (0 ) − L i 10V 1 4 解 电 感 短 路

求初始值的步骤: 1.由换路前电路(一般为稳定状态)求4c(0)和iz(0): 2.由换路定律得4c(0))和iz(0)。 3.画0等效电路。 a,换路后的电路 p.电容用电压源替代 电感用电流源替代 (取0时刻值,方向与原假定的电容 电压、电感电流方向相同)。 4.由0电路求所需各变量的0*值
求初始值的步骤: 1. 由换路前电路(一般为稳定状态)求uC(0-)和iL (0-); 2. 由换路定律得 uC(0+ ) 和 iL (0+ )。 3. 画0 +等效电路。 4. 由0 +电路求所需各变量的0 +值。 b. 电容用电压源替代 电感用电流源替代 a. 换路后的电路 (取0 +时刻值,方向与原假定的电容 电压、电感电流方向相同)
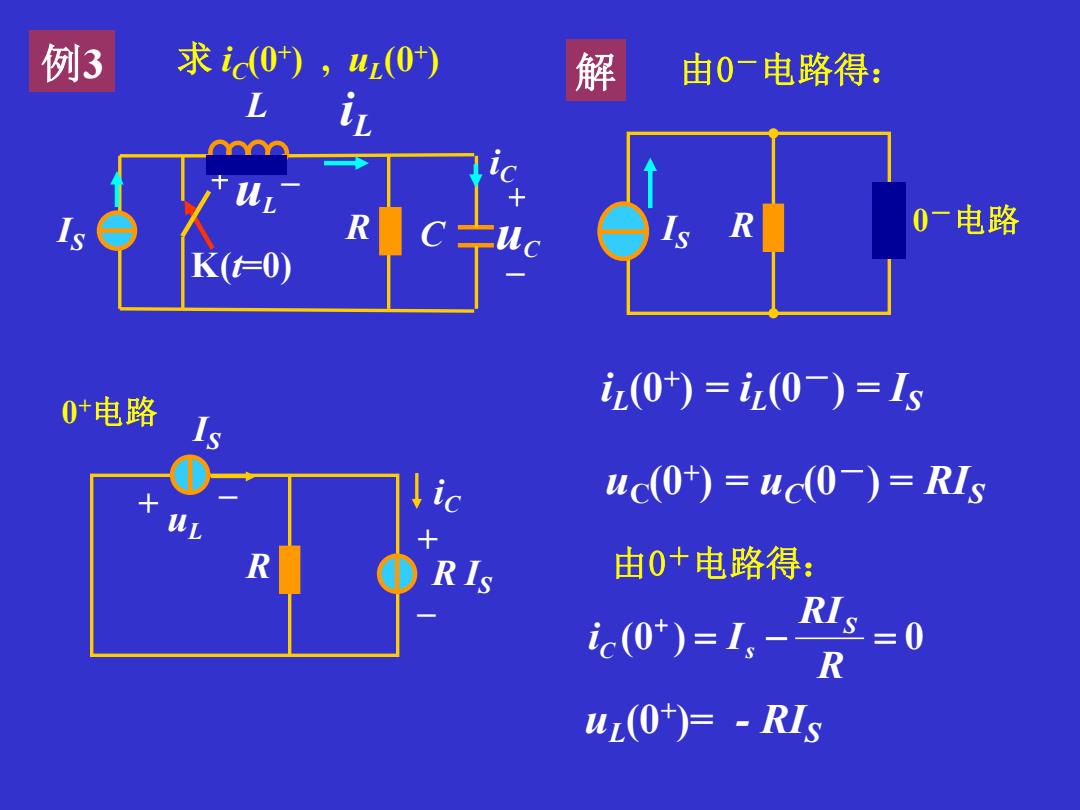
例3 求ic0),uz(0*) 解 由0一电路得: L 0一电路 K(t=0) 0*电路 iz(0)=z(0-)=Is uc(0)uc(0)=RIs RIs 由0+电路得: ic(0*)=1,- R1s=0 R uL(0)=RIs
iL (0+ ) = iL (0-) = IS uC(0+ ) = uC(0-) = RIS uL (0+ )= - RIS 求 iC(0+ ) , uL (0+ ) (0 ) = − = 0 + R RI i I S C s 例3 K(t=0) + u – L iL C + – uC L IS R iC 解 0 +电路 uL + – iC R IS R IS + – I R 0-电路 S 由0-电路得: 由0+电路得:
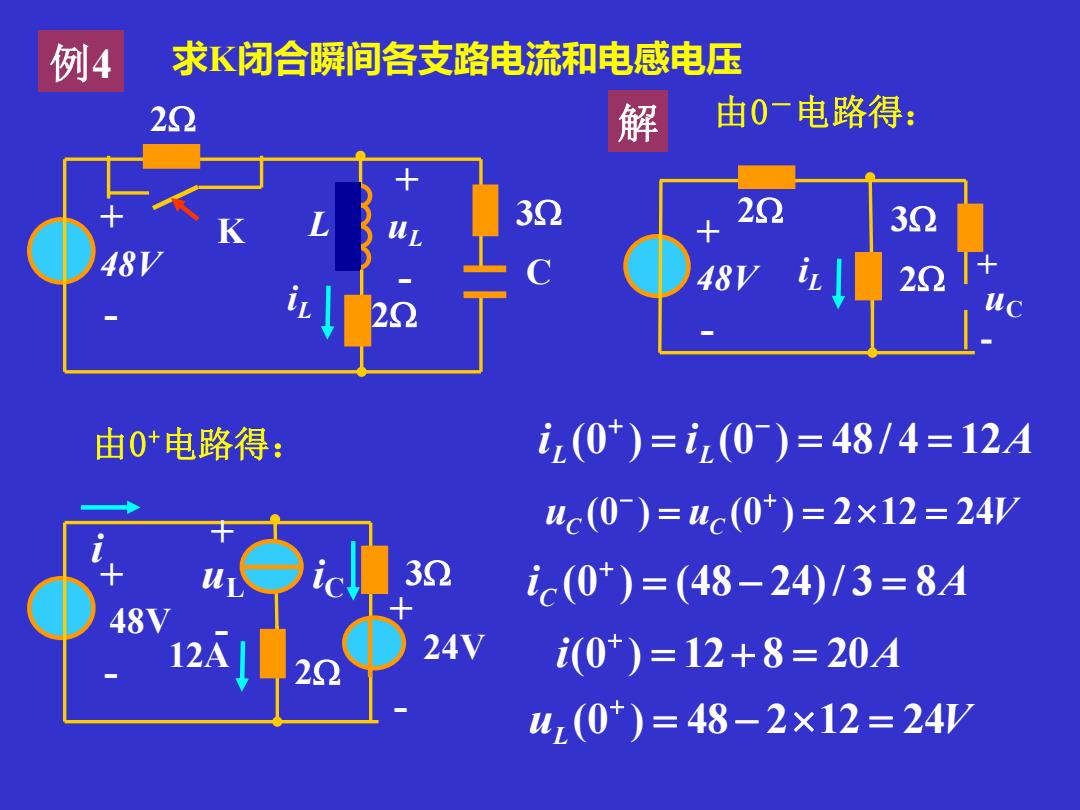
例4 求K闭合瞬间各支路电流和电感电压 20 解 由0一电路得: 3 22 30 48 48V 20 22 由0*电路得: i2(0)=i(0)=48/4=12A uc(0)=uc(0*)=2×12=24 32 ic(0*)=(48-24)/3=8A 48V L20 24V i(0*)=12+8=20A u,(0)=48-2×12=24
uC (0 ) = uC (0 ) = 212 = 24V − + i L (0 ) = i L (0 ) = 48/ 4 = 12A + − 例4 iL + uL - K L 2 + - 48V 3 2 C 求K闭合瞬间各支路电流和电感电压 解 由0-电路得: 12A 24V + - 48V 3 2 + - i iC + - uL 由0 +电路得: i C (0 ) = (48 − 24)/ 3 = 8A + i(0 ) = 12+ 8 = 20A + uL (0 ) = 48− 212 = 24V + iL 2 + - 48V 3 2 + - uC
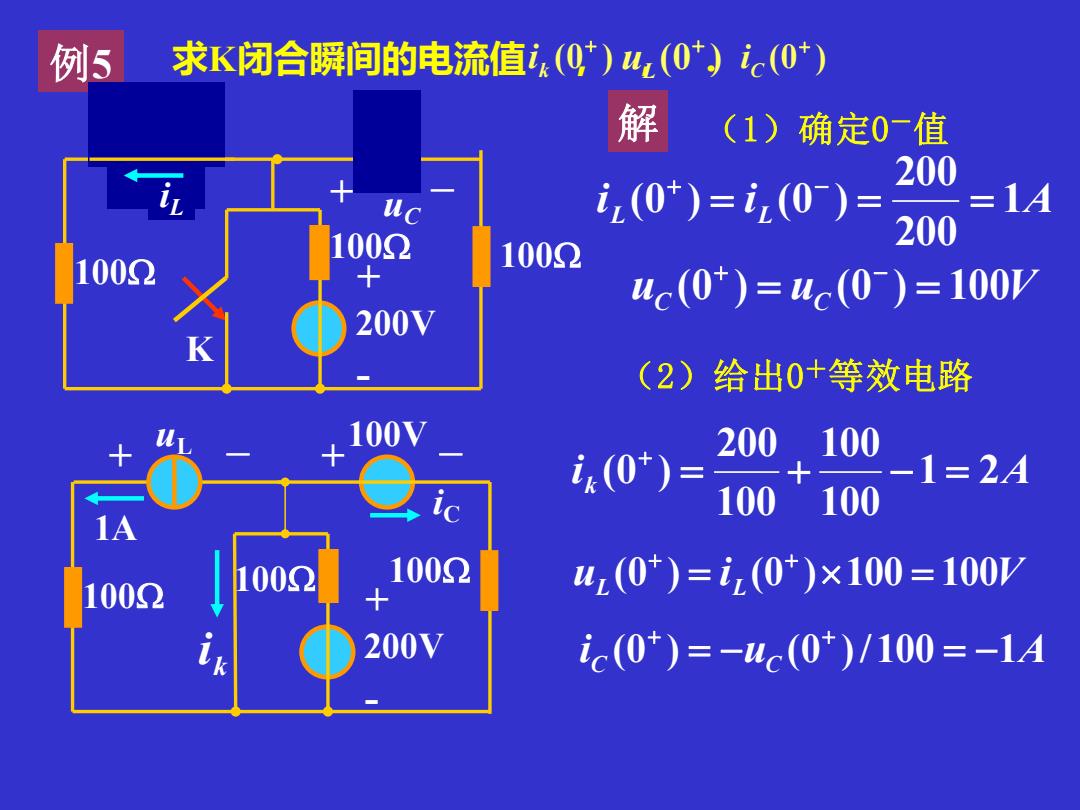
例5 求K闭合瞬间的电流值,(Q,)w2(0)ie(0*) 解 (1)确定0一值 200 z(0*)=2(0)= =1A 100Ω 200 1002 1002 uc(0*)=uc(0)=100Y 200V (2)给出0+等效电路 100V 200 100 (0*)= -1=2A 100 100 1A 1002 1002 1002 4z(0*)=i2(0*)×100=100 + 200V ic(0*)=-uc(0*)/100=-1A
例5 iL + 200V - L K 100 + uC 100 100 C - 解 (1)确定0-值 i L i L 1A 200 200 (0 ) = (0 ) = = + − uC (0 ) = uC (0 ) = 100V + − (2)给出0+等效电路 i k 1 2A 100 100 100 200 (0 ) = + − = + uL (0 ) = i L (0 )100 = 100V + + i C (0 ) = −uC (0 )/100 = −1A + + 1A + 200V - 100 + 100V 100 100 - k i + uL - iC 求K闭合瞬间的电流值 , , . (0 ) + uL (0 ) + C (0 ) i + k i

线性方程 一阶线性微分方程的标准形式: d +P(x)y=2(x) dx 当Q(x)=0,上述方程称为齐次的. 当Q(x)≠0,上述方程称为非齐次的. 例如 dx =xsint+t2,线性的; dx =y+x2, dt y-2y=3,y-c0sy=1, 非线性的
P(x) y Q(x) dx dy + = 一阶线性微分方程的标准形式: 当Q(x) = 0, 上述方程称为齐次的. 上述方程称为非齐次的. 一、线性方程 例如 , 2 y x dx dy = + sin , 2 x t t dt dx = + yy − 2xy = 3, y − cos y = 1, 线性的; 非线性的. 当Q(x) 0

一阶线性微分方程的解法 1.线性齐次方程 +P(x)y=0. d (使用分离变量法) =-Pe,∫变=-了PL, d n=-∫P(x)dx+nC, 齐次方程的通解为y=Cef恤
+ P(x) y = 0. dx dy P(x)dx, y dy = − ( ) , = − P x dx y dy ln y = − P(x)dx + ln C, 齐次方程的通解为 . ( ) = − P x dx y Ce 1. 线性齐次方程 一阶线性微分方程的解法 (使用分离变量法)

2.线性非齐次方程 少+Px)y=2(x. 讨论 两边积分ny=-∫Pu 设∫2k为r ny=x)-∫P(x)ak, 即y=e"e-jp(x u(x)
2. 线性非齐次方程 P(x) y Q(x). dx dy + = 讨论 ( ) , ( ) P x dx y Q x y dy = − 两边积分 ( ) , ( ) ln = dx − P x dx y Q x y ( ), ( ) dx v x y Q x 设 为 ln ( ) ( ) , y = v x − P x dx − = v x P x dx y e e 即 ( ) ( ) u(x)