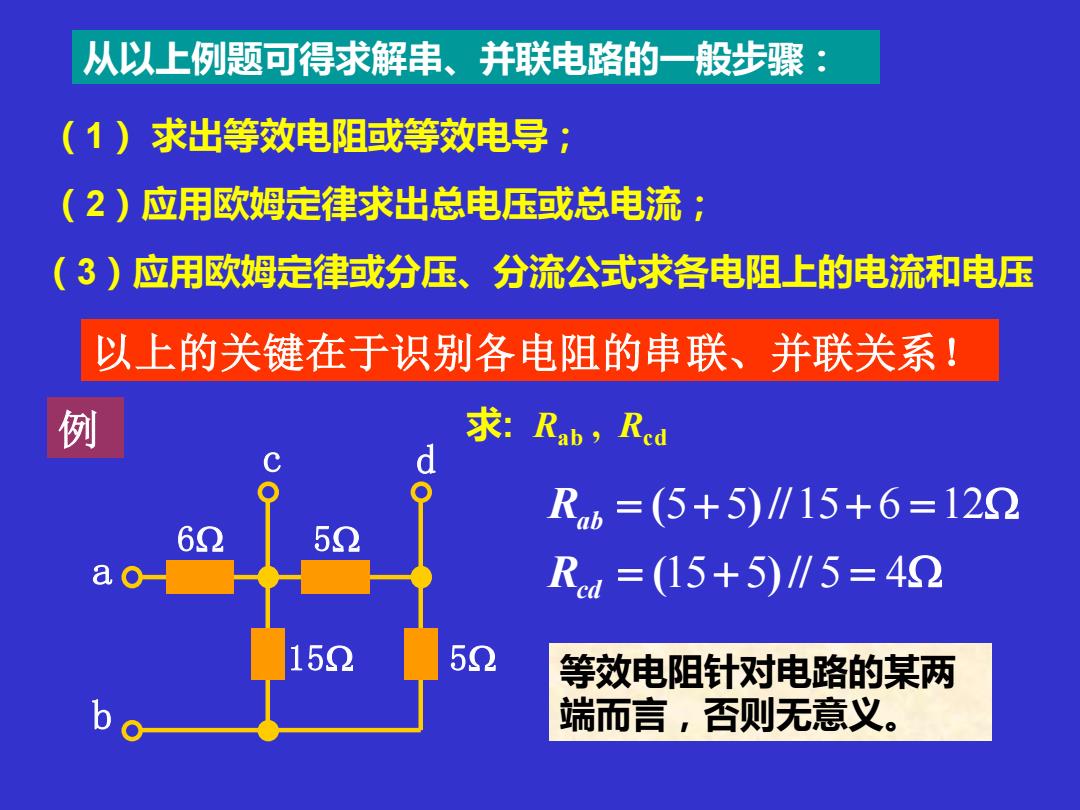
从以上例题可得求解串、并联电路的 般步骤 (1)求出等效电阻或等效电导: (2)应用欧姆定律求出总电压或总电流: (3)应用欧姆定律或分压、分流公式求各电阻上的电流和电压 以上的关键在于识别各电阻的串联、并联关系! 例 求:Pb,Rcd R=(5+5)/15+6=122 6① 50 Ra=(15+5)1∥5=42 152 52 等效电阻针对电路的某两 端而言,否则无意义
从以上例题可得求解串、并联电路的一般步骤: (1) 求出等效电阻或等效电导; (2)应用欧姆定律求出总电压或总电流; (3)应用欧姆定律或分压、分流公式求各电阻上的电流和电压 以上的关键在于识别各电阻的串联、并联关系! 例 6 15 5 5 c d b a 求: Rab , Rcd Rab = (5+ 5)//15+ 6 =12 Rcd = (15+ 5)// 5 = 4 等效电阻针对电路的某两 端而言,否则无意义
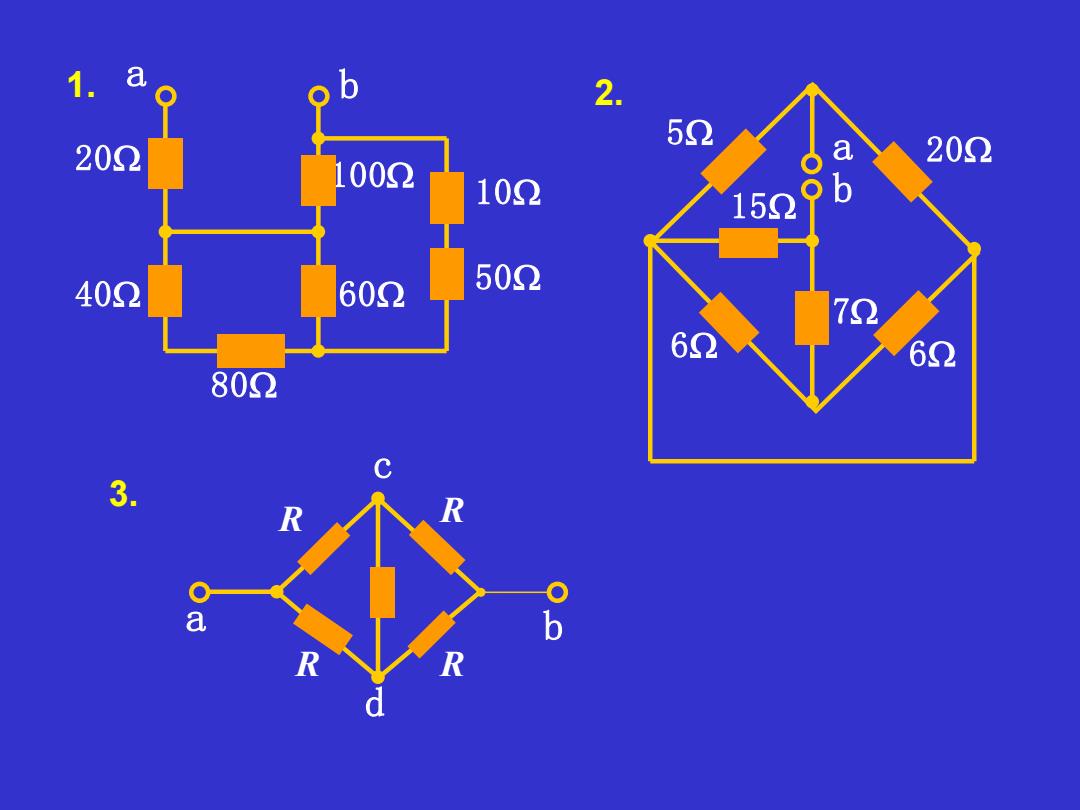
a 1. 2. 5 202 a 200 1002 102 152 402 602 50Q 60 62 80① C 3. R R a b R
60 100 50 10 b a 40 80 20 15 20 b a 5 6 6 7 a b c d R R R R 1. 3. 2

例 求:Rab a 202 1002 202 1002 100 602 1202 602 600 502 80① a a 202 1002 202 1002 1000 602 402 Rab=702
例 60 100 50 10 b a 40 80 20 求: Rab 100 60 b a 40 20 100 100 b a 20 60 100 60 b a 120 20 Rab=70
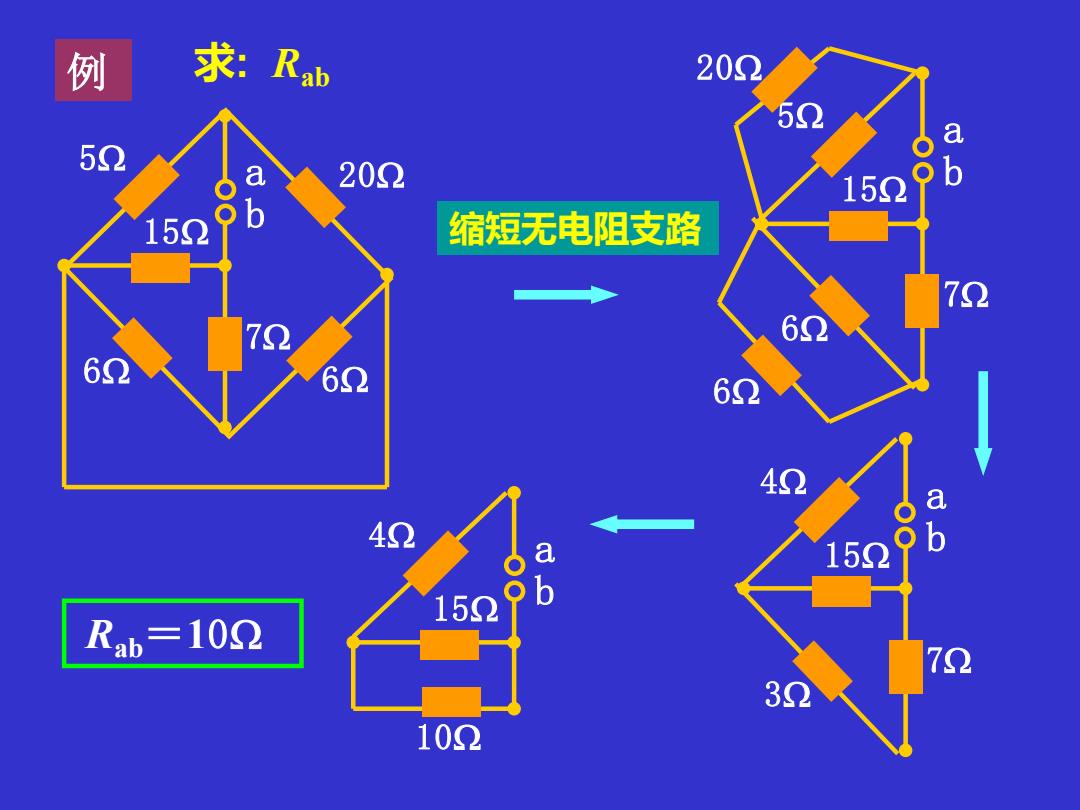
例 求:RaD 20① 52 a 52 200 152 152 缩短无电阻支路 7Ω 62 62 a 15 b 15 Rab=102 7Ω 39 102
例 15 20 b a 5 6 6 7 求: Rab 15 b a 4 3 7 15 20 b a 5 6 6 7 15 b a 4 10 Rab=10 缩短无电阻支路
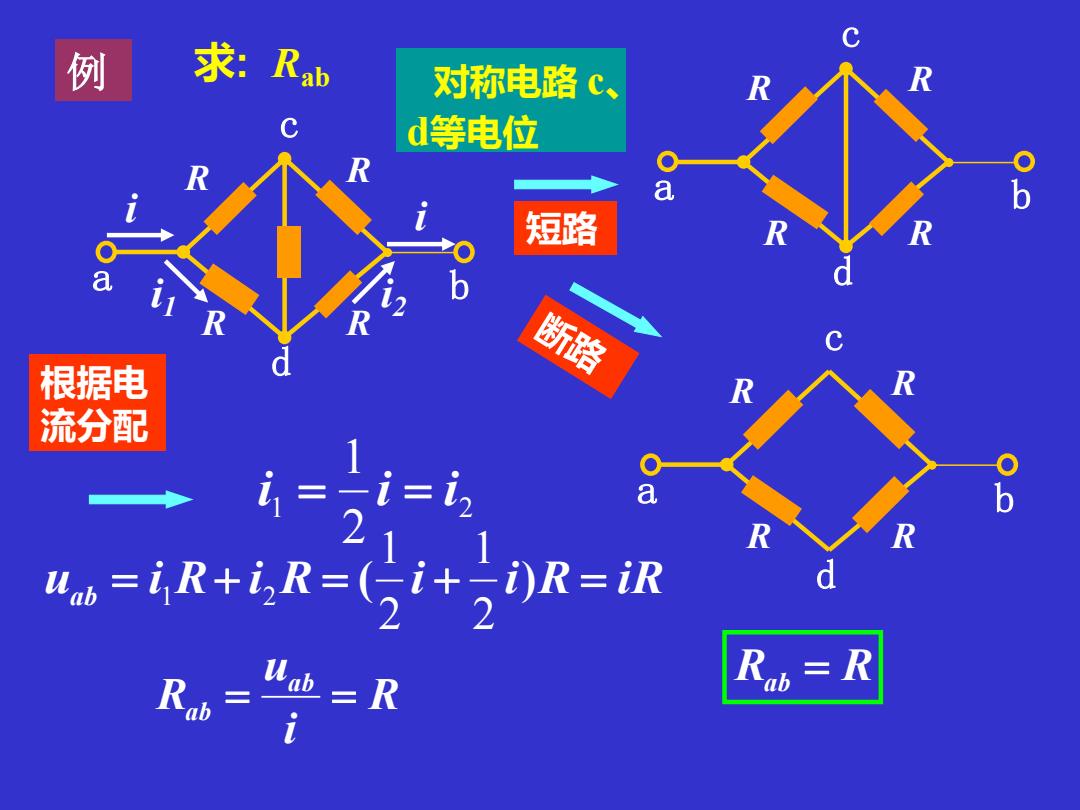
例 求:Rab 对称电路c、 R d等电位 短路 断路 根据电 流分配 =i= a 0 1 R ub=R+i2R=(行i+)R=iR R-=R R =R
例 a b cd RR RR 求: Rab 对称电路 c 、 d等电位 a b cd RR RR a b cd RR RR i i1 i i2 1 2 21 i = i = i uab = i R + i R = ( i + i ) R = i R 21 21 1 2 R i u R ab ab = = Rab = R 短路 根据电 流分配
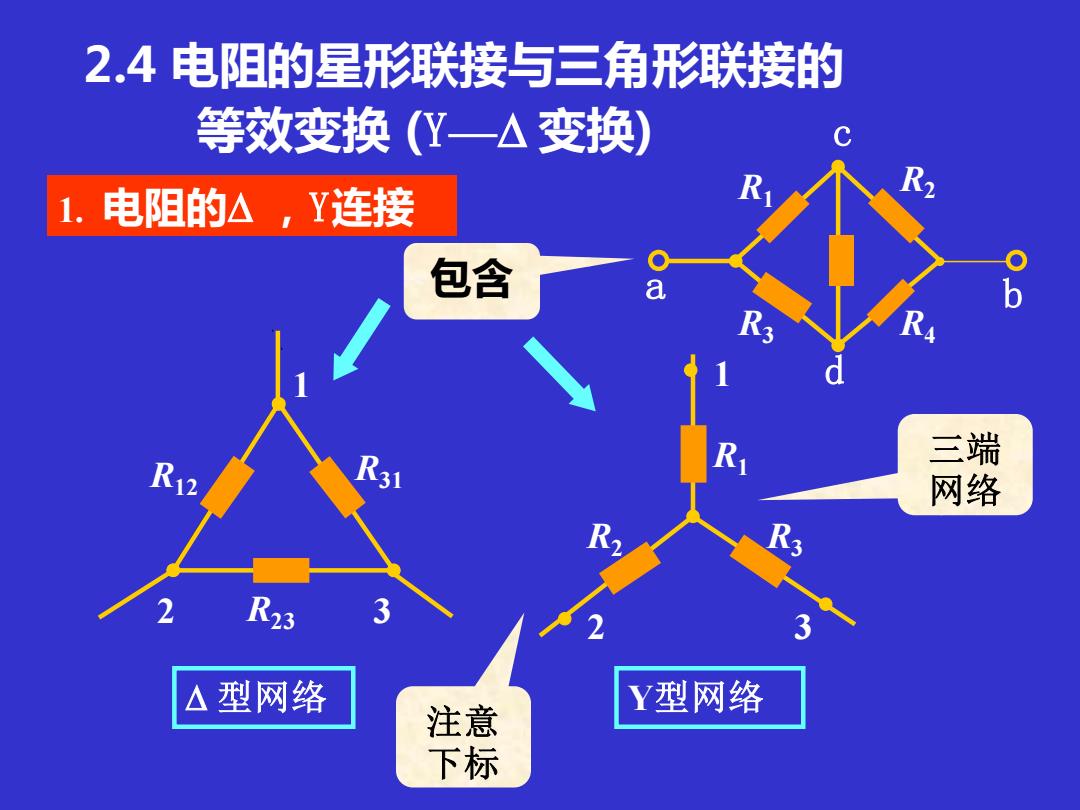
2.4电阻的星形联接与三角形联接的 等效变换(Y一△变换) 1.电阻的△,Y连接 包含 三端 网络 R23 △ 型网络 Y型网络 注意 下标
2.4 电阻的星形联接与三角形联接的 等效变换 (Y— 变换) 1. 电阻的 ,Y连接 型网络 Y型网络 R12 R31 R23 1 2 3 R1 R2 R3 1 2 3 a b c d R1 R2 R3 R4 包含 三端 网络 注意 下标
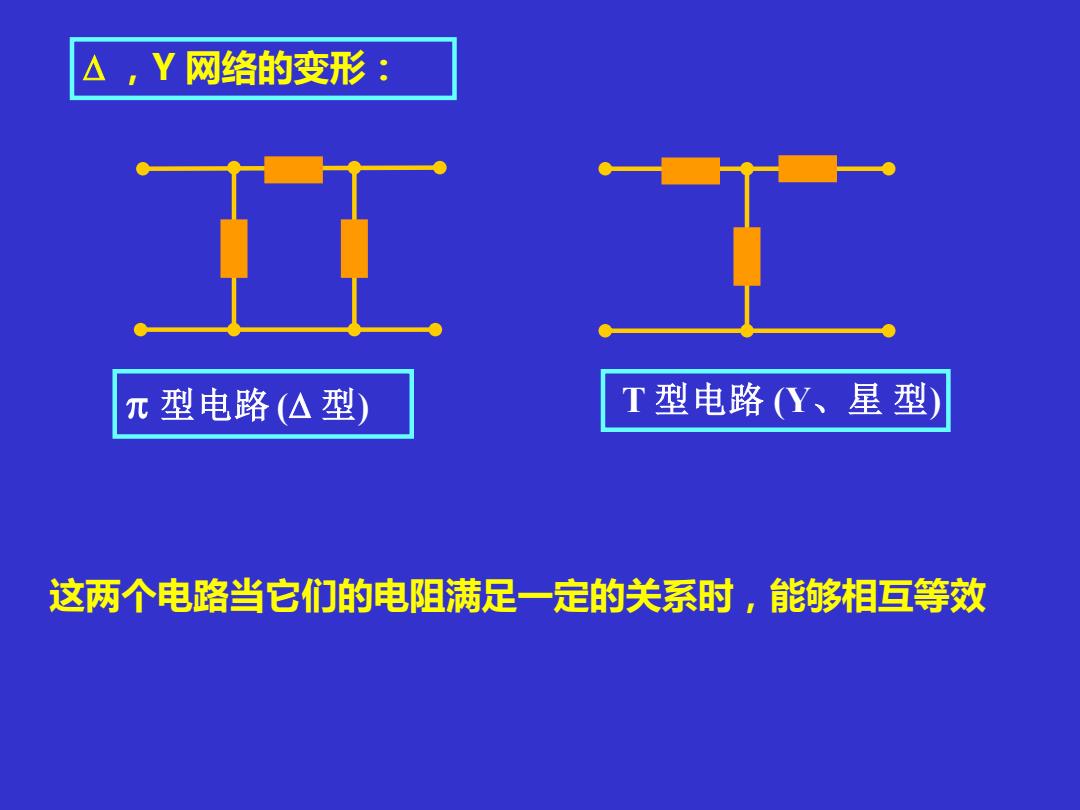
△,Y网络的变形: π型电路(△型 T 型电路(Y、星型 这两个电路当它们的电阻满足一定的关系时,能够相互等效
,Y 网络的变形: 型电路 ( 型) T 型电路 (Y、星 型) 这两个电路当它们的电阻满足一定的关系时,能够相互等效
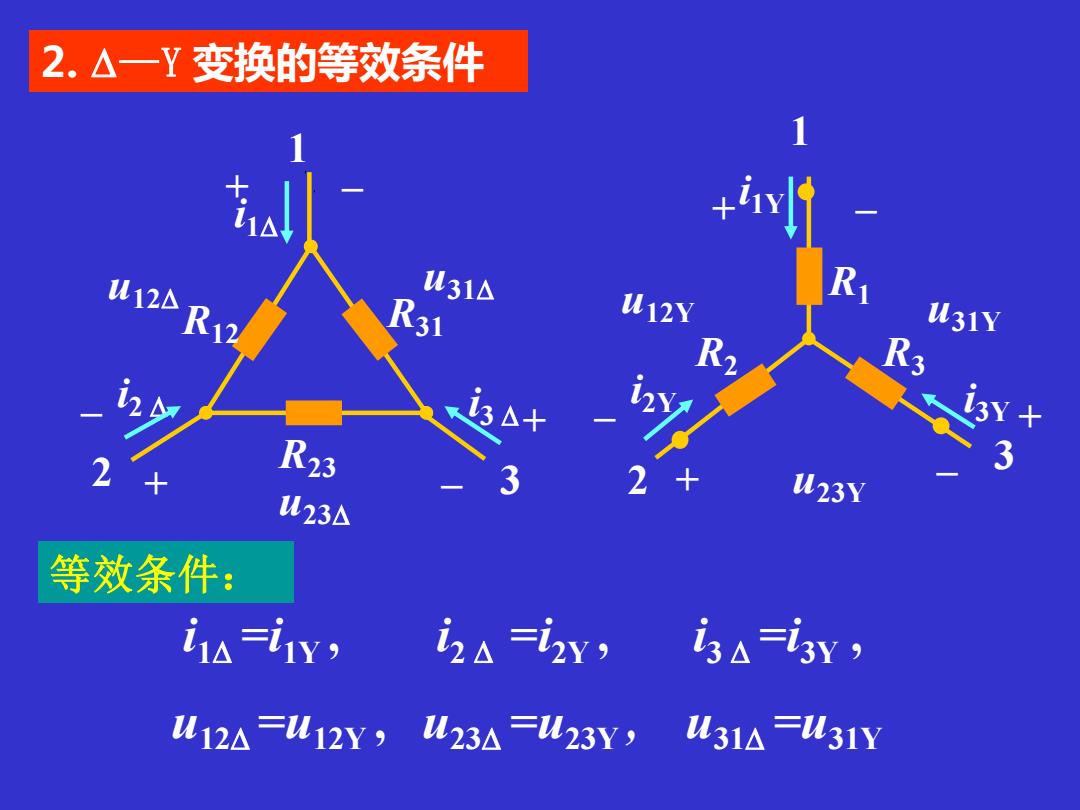
2.△一Y变换的等效条件 +N1 2R2 W31△ R R31 W12Y 31Y R3 R23 U23△ W23Y 等效条件: in=iy, 2a=i2y,3A=3y, L12A=U12Y,M23A=423Y, L31△=u31Y
u23 R12 R31 R23 i3 i2 i1 1 2 3 + + + – – – u12 u31 R1 R2 R3 i1Y i2Y i3Y 1 2 3 + + – + – – u12Y u23Y u31Y i1 =i1Y , i2 =i2Y , i3 =i3Y , u12 =u12Y , u23 =u23Y , u31 =u31Y 2. —Y 变换的等效条件 等效条件:
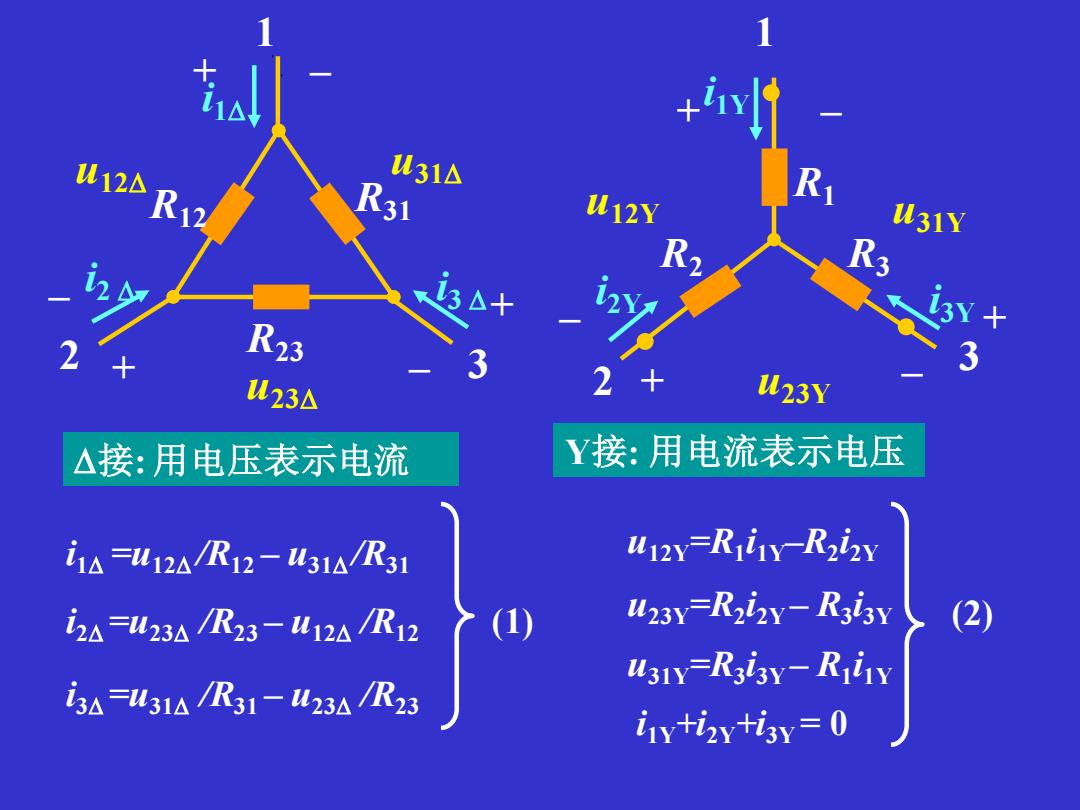
+y1 U2少R2 u31△ 31 W12Y U31Y R R23 U23△ W23Y △接:用电压表示电流 Y接:用电流表示电压 i1A=u12A/R12-431A/R31 412y=RiY-R2iy i2A=u23A/R23-412A/R12 (1) 423Y=R2i2Y-R3i3Y (2) u31y=R3i3y-Riiy i3A=u31A/R31-423AR23 ilytizy+isy 0
Y接: 用电流表示电压 u12Y=R1 i1Y–R2 i2Y 接: 用电压表示电流 i1Y+i2Y+i3Y = 0 u31Y=R3 i3Y – R1 i1Y u23Y=R2 i2Y – R3 i3Y i3 =u31 /R31 – u23 /R23 i2 =u23 /R23 – u12 /R12 i1 =u12 /R12 – u31 /R31 u23 R12 R31 R23 i3 i2 i1 1 2 3 + + + – – – u12 u31 R1 R2 R3 i1Y i2Y i3Y 1 2 3 + + – + – – u12Y u23Y u31Y (2) (1)

由式(2)解得: 产元微限风汉 412yR3-W31yR2 i1A=u12AR12-431△R31 423YR1-412yR3 izy=RRa+RR;+RyR (3) i2A=u23A/R23-u12A/R12 (1) usly R2 -423y R i3A=l31△R31-423AR23 isy=RRg+RRs+RR 根据等效条件,比较式(3)与式(1),得Y型→△型的变换条件: RR R2=R1+R2+ GG, R3 G12 G1+G2+3 R3=R2+R3+ R,3 G.G R 或 G23 G1+G2+G3 R1=R3+R1+ RRI G.G R2 G3=G,+G2+G3
1 2 2 3 3 1 12Y 3 31Y 2 1Y R R R R R R u R u R i + + − = 1 2 2 3 3 1 23Y 1 12Y 3 2Y R R R R R R u R u R i + + − = 1 2 2 3 3 1 31Y 2 23Y 1 3Y R R R R R R u R u R i + + − = 由式(2)解得: i3 =u31 /R31 – u23 /R23 i2 =u23 /R23 – u12 /R12 i1 =u12 /R12 – u31 /R31 (1) (3) 根据等效条件,比较式(3)与式(1),得Y型→型的变换条件: 2 3 1 31 3 1 1 2 3 23 2 3 3 1 2 12 1 2 R R R R R R R R R R R R R R R R R R = + + = + + = + + 1 2 3 3 1 31 1 2 3 2 3 23 1 2 3 1 2 12 G G G G G G G G G G G G G G G G G G + + = + + = + + = 或