
第9章选代举习控制 意代单习控暖合于有为性圆的被对康,过地代整 选代举习(Lc,terative Learning Control)的题量录钉由 实东控制中存在一类轨迹穿问题,它的控制任务是博找控制牌 日*单请Jchiyama于H978年调出。于184年由Arimoto等人最出丁 正站某弹拉制同标的放曹。地代学好拉州方线不食酸于菜统的精闲 使得被控对象编出山在有限时问瓜止沿著整个期里轨迹实现零 开的性的完。这数草请滑落人庄复过根中速来端意常标达到锦 最学型,能在地定的时时范圆内.上以常剪单的续实调不纯定性 误差林迹球避。这列课琼问是是具有扰战性的控制问题, 高的战性盟明合孙客服旋的花制,并高定果草输亮票想轨克,园 盟行为的筒单原通。地使海人有、合中黄性*卖量钠工机哪 人们在处理实际场合中的重复操作任务时,柱柱依据对象的可重复 人快填高精度难典行辣速事任务,其高本量选是对于一个在有限时 面一经推出,在为拉州球州测丁广花的提用, 动态行为与期望行为的差距来离整决策,通过重复操作,使得对像行 周区同上教行盖是库在务的机鼻人,利用前一次或输几次操作时调 处代学习控圳仿使具有很的工青景,这业青限招执行请 为与期卫行为的配合达到要求。这时,衡量动态行为的渐标是某种满 骨的误维物喜正控输入,使海城复任务在下一次操作拉超中触 仰界换、喷除、纯泥、搬这体美在务的工最人指◆物号为周 意惭标。 舞更好,加此不所量复。直更在整十时间区风上输出轨诚章上期量 湘国的风眼果集:最控机床,歌流光查地原菜机输树境中使用 教迹。 的壶标量机峰, 由于达代学习控制核物了人魅学习和白我调节的功施,因而是一 式中,:e段:”,”分别为系统的状态,输出和输入变量, 选代学习控制可分为开环学习和闭环学习。 种典型的智能控制方法,经历了三十多年的发展,迷代学习控制已成 、小、g山为适当绅数的内量函数,其结构与数数均未知。若期望控 开环学习控制的方法是:第k+1次的控制等于第k次控制再加上第k欢 为智能控制中具有严格数学抽选的一个分支。日前选代学习控制在学 制存在则选代学习控制的日标为:给定期望编出,们和年次运 输出误差的校正项。即 习算法。收敏性、鲁棒性、学习速度及工程应用研究上取得了很大的 行的初始状态1,©要求在给定的时洞:和,】内按照一定的学习控制 进煨。 算法通过多次重复的运行,使控制输入马,,一,叫,而系统输出,→ s.cin-Lin..( 9.4) 91芯本6圆 第k次运行时。式(91)表示为: 闭环学习薰略是:取第K+1次运行的误差作为学习的修正项,即 设被控对象的动态过程为 (92购 n-uu明 9.5 但.1) 跟踪误差为 式中。L为线性城非线性算子。 ()-fsrir).yir-glunokr) -y-0 9.3 1
1 第9章 迭代学习控制 实际控制中存在一类轨迹跟踪问题,它的控制任务是寻找控制律 ,使得被控对象输出 在有限时间 上沿着整个期望轨迹实现零 误差轨迹跟踪。这列跟踪问题是具有挑战性的控制问题。 人们在处理实际场合中的重复操作任务时,往往依据对象的可重复 动态行为与期望行为的差距来调整决策。通过重复操作,使得对象行 为与期望行为的配合达到要求。这时,衡量动态行为的指标是某种满 意指标。 u t y t 0,T 迭代学习控制(ILC,Iterative Learning Control)的思想最初由 日本学者Uchiyama于1978年提出,于1984年由Arimoto等人做出了 开创性的研究。这些学者借鉴人们在重复过程中追求满意指标达到期 望行为的简单原理,成功地使得具有强耦合非线性多变量的工业机器 人快速高精度地执行轨迹跟踪任务。其基本做法是对于一个在有限时 间区间上执行轨迹跟踪任务的机器人,利用前一次或前几次操作时测 得的误差信息修正控制输入,使得该重复任务在下一次操作过程中做 得更好。如此不断重复,直至在整个时间区间上输出轨迹跟踪上期望 轨迹。 迭代学习控制适合于具有重复运动性质的被控对象,通过迭代修 正达到某种控制目标的改善。迭代学习控制方法不依赖于系统的精确 数学模型,能在给定的时间范围内,以非常简单的算法实现不确定性 高的非线性强耦合动态系统的控制,并高精度跟踪给定期望轨迹,因 而一经推出,就在运动控制领域得到了广泛的运用。 迭代学习控制方法具有很强的工程背景,这些背景包括:执行诸 如焊接、喷涂、装配、搬运等重复任务的工业机器人;指令信号为周 期函数的伺服系统;数控机床;磁盘光盘驱动系统;机械制造中使用 的坐标测量机等。 由于迭代学习控制模拟了人脑学习和自我调节的功能,因而是一 种典型的智能控制方法。经历了三十多年的发展,迭代学习控制已成 为智能控制中具有严格数学描述的一个分支。目前,迭代学习控制在学 习算法、收敛性、鲁棒性、学习速度及工程应用研究上取得了很大的 进展。 9.1 基本原理 设被控对象的动态过程为 x x u ( ) ( ( ), ( ), ) t f t t t ,y x u ( ) ( ( ), ( ), ) t g t t t (9.1) 式中, 、 、 分别为系统的状态,输出和输入变量, 、 、 为适当维数的向量函数,其结构与参数均未知。若期望控 制 存在,则迭代学习控制的目标为:给定期望输出 和每次运 行的初始状态 ,要求在给定的时间 内,按照一定的学习控制 算法通过多次重复的运行,使控制输入 ,而系统输出 第k 次运行时,式(9.1) 表示为: (9.2) 跟踪误差为 (9.3) n x R m y R r u R f ( ) g ( ) d u ( )t d y ( )t (0) k x t T 0, d ( ) ( ) k u u t t d ( ) ( ) k y y t t ( ) ( ( ), ( ), ) k k k x x u t f t t t ( ) ( ( ), ( ), ) k k k y x u t g t t t d ( ) ( ) ( ) k k e y y t t t 迭代学习控制可分为开环学习和闭环学习。 开环学习控制的方法是:第k+1次的控制等于第k次控制再加上第k次 输出误差的校正项,即 (9.4) 闭环学习策略是:取第K+1次运行的误差作为学习的修正项,即 (9.5) 式中,L为线性或非线性算子。 1 ( ) L( ( ), ( )) k k k t t t u u e 1 1 ( ) L( ( ), ( )) k k k t t t u u e

9.2蓄体地代弹习控算接 此养,延有南地代学整常法、兼食造代录习量的选、意店于地 932端信同量 作单习提时体效市反编前维造代学可法体独博, Arimoto年黄先峰出丁鱼性时变选编基旅的D里选代学习恤到停 得边代苹好维木量计控时,只要■比项得特独 豆3造代厚用指纳关故球 对康的监试进微微号,在地整制批水中,流代平习融焉秋州点 马-马元0 9. 立3.1单习常法的晚轻最敏借 开抛。口始加和州本减和地地岛。几所有的黄性证则要水州条 式中,「为常量州撞矩韩,在D业算法的盖随上相验出真丁P业、 输安性使教性何渐究当单习神被接家镇境见什么本并树,地代 件是州同的,解进代学牙数地中的抛州间置一直是人地求物周 P列业、PD进代#习撞制牌,从一量童义本滑它打事是PD型进代 习州过寸是造定收教的。南地的量定鞋量延了整增学习次量的物, 标之一,同前已璃出的地代单习产州算城大多源要家进编欢运行时胸 单习拉制掉的绿形式,PD透代学习撞制辣家示为 控制保不突放,绳,对于草好性制那桌有,仅仅南具发有标意义 地快毒定道载壶对应的地状喜上即喷蜂冰米 )马,0++,价+g:(8刀 的。只有使平习址其值才恤置的控为茶意义下量瓷的 (9.8) 整州。轨是时学习州的绿盖木的两求,微学墙在刺出新特单习棒的调 墙那镜的始本不荆速上,在用铁地钠常一氧小的城钠 式中「、小、¥为学习增拉序,幕放中的满进物惠使用常为开许境 时,蓄于对时桌的业银慢。轴由丁批黄的琳并。Arimoto由最物 时,是常丝类河白维为单习牡制的海排性具直听究 代单习业响。如果使用则常为环地代单习壮铺,如果同时使用市 舞曲PD单时,仅新物性核在夏单降下的量史性故条 测靠为开东造代学习控响, 件作丁项 9.33学习境发询厘 9.34音神闻酒 且.4被学嫩毫璃雕地代学习控制仿高实州 在选代苹习常独研汽中,其收放绿件盖术上解局在单习次兼:一示 处代学习社通地的绳出有律厚的工青最,置此仅仅在无干找 41控前D没计 下输出的。圆在实际应用据合,举习次最:+x是篇鼻设有任★实霹 常件下时地收业性铜题绳不等韵,还应时地存在各州干找的情形下票 考准一个关节的机人,其动结性可以由以下一前中州性缘分方 意文的。因此加有使造代学习过福更快地收敏于舞温管具进代学习 策的果膝性施。一个得线行静选代学习控制原能敬丁存始物够 意捕地 控斜将汽中的另一个量要同题。 外,还减本硫少存在状喜批地、师声、抛入挑动尊客种干找.鲁 叫q54c4+Ggj-r- (9.9) 选代季习控响林视上局一群满钟腔树锐术,大解分学习律厚管正 神性何厘时地存在客料干就时透代学可拉响票策的佩性施。具体地 式中,4取为共节角位事量,(回a双为最人的性麻,C() 喷丁学习收蒙的充分并,祖收就地皮还局很量。可利用套次学习过 视,一十地代单闪控原统局鲁神游,局湘果转在各种有界干枕的形 悬中将测的加来球进镇样习过室的速麦。加,禾用高前选代拉 响下,其德代教旋物收敏到阑慢克的端纳,可墙这整干找湖雕时 老示青化力和哥民力,G(k为力项:为挂力把。为各 种提塘和找地。 制算波、意境右四于的单习律、用墙前球夏现等方陵来南造 ,意代林建会收敏到用里软速 苹习株,可使收敏速度大大加快。 世系装要康的速铁造为,件,血,小,续算次输出为, ◆0-小-间- 2
2 9.2 基本迭代学习控制算法 Arimoto 等首先给出了线性时变连续系统的D型迭代学习控制律 (9.6) 式中, 为常数增益矩阵。在D 型算法的基础上,相继出现了P 型、 PI 型、PD 型迭代学习控制律。从一般意义来看它们都是PID型迭代 学习控制律的特殊形式,PID迭代学习控制律表示为 (9.7) 式中, 、 、 为学习增益矩阵。算法中的误差信息使用称为开环迭 代学习控制,如果使用 则称为闭环迭代学习控制,如果同时使用和 则称为开闭环迭代学习控制。 1 ( ) ( ) ( ) k k k t t t u u Γe Γ 1 ( ) ( ) ( ) ( ) ( )d t k k k k k t t t t 0 u u Γe Φe Ψ e Γ Φ Ψ 此外,还有高阶迭代学习控制算法、最优迭代学习控制算法、遗忘因子迭 代学习控制算法和反馈-前馈迭代学习控制算法等。 9.3 迭代学习控制的关键技术 9.3.1 学习算法的稳定性和收敛性 稳定性与收敛性问题是研究当学习律与被控系统满足什么条件时,迭代 学习控制过程才是稳定收敛的。算法的稳定性保证了随着学习次数的增加, 控制系统不发散,但是,对于学习控制系统而言,仅仅稳定是没有实际意义 的,只有使学习过程收敛到真值,才能保证得到的控制为某种意义下最优的 控制。收敛是对学习控制的最基本的要求,多数学者在提出新的学习律的同 时,基于被控对象的一些假设,给出了收敛的条件。例如,Arimoto在最初 提出PID型学习控制律时,仅针对线性系统在D型学习律下的稳定性和收敛条 件作了证明 9.3.2 初始值问题 运用迭代学习控制技术设计控制器时,只需要通过重复操作获得的受控 对象的误差或误差导数信号。在这种控制技术中,迭代学习总要从某初始点 开始,初始点指初始状态或初始输出。几乎所有的收敛性证明都要求初始条 件是相同的,解决迭代学习控制理论中的初始条件问题一直是人们追求的目 标之一。目前已提出的迭代学习控制算法大多数要求被控系统每次运行时的 初始状态在期望轨迹对应的初始状态上,即满足初始条件: (9.8) 当系统的初始状态不在期望轨迹上,而在期望轨迹的某一很小的邻域内 时,通常把这类问题归结为学习控制的鲁棒性问题研究。 d (0) (0), 0,1,2, k x x k … 9.3.3 学习速度问题 在迭代学习算法研究中,其收敛条件基本上都是在学习次数 下给出的。而在实际应用场合,学习次数 显然是没有任何实际 意义的。因此,如何使迭代学习过程更快地收敛于期望值是迭代学习 控制研究中的另一个重要问题。 迭代学习控制本质上是一种前馈控制技术,大部分学习律尽管证 明了学习收敛的充分条件,但收敛速度还是很慢。可利用多次学习过 程中得到的知识来改进后续学习过程的速度,例如,采用高阶迭代控 制算法、带遗忘因子的学习律、利用当前项或反馈配置等方法来构造 学习律,可使收敛速度大大加快。 k k 9.3.4 鲁棒性问题 迭代学习控制理论的提出有浓厚的工程背景,因此仅仅在无干扰 条件下讨论收敛性问题是不够的,还应讨论存在各种干扰的情形下系 统的跟踪性能。一个实际运行的迭代学习控制系统除了存在初始偏移 外,还或多或少存在状态扰动、测量噪声、输入扰动等各种干扰。鲁 棒性问题讨论存在各种干扰时迭代学习控制系统的跟踪性能。具体地 说,一个迭代学习控制系统是鲁棒的,是指系统在各种有界干扰的影 响下,其迭代轨迹能收敛到期望轨迹的邻域内,而当这些干扰消除时 ,迭代轨迹会收敛到期望轨迹。 9.4 机械手轨迹跟踪迭代学习控制仿真实例 9.4.1控制器设计 考虑一个关节的机器人,其动态性能可以由以下二阶非线性微分方 程描述: (9.9) 式中: 为关节角位移量, 为机器人的惯性矩阵, 表示离心力和哥氏力, 为重力项, 为控制力矩, 为各 种误差和扰动。 设系统所要跟踪的期望轨迹为 , 。系统第次输出为 令 。 d D q q C q q q G q τ , τ n q R n n D q R , n C q q R n G q R n τ R d n τ R yd t t T 0, yi t e y y i i t t t d

在学习开始时,系统的始状态为气,心。学习控制的任务为通过学 9.42你其实潮 q-化+d4gm4+d以m4+为)q42m叫国+) 习控制律设计”,使第1次运动误差。心码减少. 针对二关节机敏平,升阳一种视是人PD度造代单好控制的齿 干援项为,[a3ara吧-<了 采用三种基于反馈的选代学习控制律: 其最计方线。针对二关节肌题人控响原能式(但.9),客使景为: (1)闭环D理 D-61 g=81 马马)+k色小-4缚 (910) 4.-4+d代+g+24aem+4+与 采用三种闭环达代学习控制律,其中M。1为D型选代学习控制,M,2 (2)闭环PD型: t-h一6+kam雨小6 为PD型选代学习产制,M,3为变增益渐意D型达代学习护制, 妇d+ a间-+k,(包-a+k-4M(911) 两个关节的位置指令分别为山和网3外为了保证被护对像初始输 (3)指数变增拉D型: c-isbe 出与拆令初值一政,取被控对像的初始状态为x间一心31叫取 马-马+K间-4K色-(9.12) PD型达代学习控制,即,3,仿真结果如图91至图93所示, G-la al Chongo of madmn ue valug of onor atd or2 wth lines i 03 0 05 图9120次地代学好韵球过 圆9-2靠20次进代学习的位置果睡 图9320次造代出中模楚喜最的收教过通 3
3 在学习开始时,系统的初始状态为 。学习控制的任务为通过学 习控制律设计 ,使第 次运动误差 减少。 采用三种基于反馈的迭代学习控制律: (1)闭环D型 (9.10) (2)闭环PD型: (9.11) (3)指数变增益D型: (9.12) x0 0 ui1 t i 1 ei1 t u u K q q k k k 1 d d 1 t t t t u u K q q K q q k k k k 1 p d 1 d d 1 t t t t t t u u K q q K q q k k k k 1 p d 1 d d 1 t t t t t t 9.4.2 仿真实例 针对二关节机械手,介绍一种机器人PD型反馈迭代学习控制的仿 真设计方法。针对二关节机器人控制系统式(9.9),各项表示为: 2 2 ij d D 2 2 2 11 1 1 2 1 2 1 2 2 1 2 2 cos c c c d d l d l l l l q I I 2 12 21 2 2 1 2 2 2 cos c c d d d l l l q l 2 22 2 2 2 c d d l I 2 2 ij c C 11 2 c hq 12 1 2 c hq hq 21 1 c hq 22 c 0 2 1 2 2 sin c h m l l q T G G G 1 2 干扰项为 机器人系统参数为 , ,, , 采用三种闭环迭代学习控制律,其中 为D型迭代学习控制, 为PD型迭代学习控制, 为变增益指数D型迭代学习控制。 两个关节的位置指令分别为 和 ,为了保证被控对象初始输 出与指令初值一致,取被控对象的初始状态为 。取 PD型迭代学习控制,即 ,仿真结果如图9-1至图9-3所示。 G d l d l q d l q q 1 1 1 2 1 1 2 2 1 2 c c g cos g cos G d l q q 2 2 2 1 2 c g cos T d 0.3sin 0.1 1 e t t 1 2 d d 1 kg 1 2 l l 0.5m 1 2 l l c c 0.25m 2 1 2 I I 0.1 kg m 2 g 9.81 m/s M 1 M 2 M 3 sin(3 )t cos(3 )t T x 0 0 3 1 0 M 3 图9-1 20次迭代学习的跟踪过程 图9-2 第20次迭代学习的位置跟踪 图9-3 20次迭代过程中误差范数的收敛过程

9.5编使时究表缘系能地代学闲视响 982想响鲁设计没妆黄性分新 非齐次一阶线性弹分方程小中)的解为: 95.1系荣箱地 真理1着由式(9.13)或(9.14)潮地的果物见下并: -co✉u斗asu倒a-C-up Arimoto情出了黄性时实地候属能 (1)-CsrW承1 0m+mM[m-4Ψ0f〔-it )=A)+ (9.13) x-c(9 (2)选代和条并章,厚o--21(o-y侧 取ok.-pA0-r》则 迪+时,有问+付,门。 馬-5.-6-s(e气r-马p 的开不P列D选代#习控州, 正喇: 由于仰-%m,s-孙-则 --是1+0 (9.14) 式(a.3)及试(2)舞a间-00-仰-o 小-g--wa-G填s- 其中,1,¥为学习增进矩裤, 则@-收-之小即承能填见地条并. -q6倒a-suu 即 将式(9.1刀两端取范数,有 e-s-q6.到ra-arr ort-ifAh.(urcop-[ab.(nep(-irjer(agdrston-h.(for(ind a种-q4l.et长eke 将PD受控制津式(9.14)代入上式,则第k+1次输出的误差为: m啡l些头lm-444t --am成4ha](9.i5) -a国u.体r-ou4M保 xmkot 中-qeW-o (9.19) 利用分部积分公式,令G.r-C(rd,有 式中 【ce)s()r(-H.(r)er-ae啡-层ct.).(hr 4m{长ae小ae 根据1范数的定文.面数扣门→r的范数为:机思/中 -cMre-会e%e (9.16) s”思6W 由于a小,¥0a小则有ke儿k儿· 将式(9.16)代入式(9.15),得 根蠡范数的定文可,面数/→心的范数为几~二/ 将式(9.19)的结果应用于下式,得: --4-会o4%* (9.17 将式9,酚两铺同要似am0w井考虑到【d,= 有 -a.a画fr抽-C到v:la(ojdolr 4
4 9.5 线性时变连续系统迭代学习控制 9.5.1 系统描述 Arimoto等给出了线性时变连续系统 (9.13) 的开环PID型迭代学习控制律: (9.14) 其中 , , 为学习增益矩阵。 t t t t t t t t x A x B u y C x 1 d d d k k k t t t t t u u Γ L Ψ e Γ L Ψ 9.5.2 控制器设计及收敛性分析 定理1 若由式(9.13)和式(9.14)式描述的系统满足如下条件: (1) ; (2)每次迭代初始条件一致,即 则当 时,有 , 。 证明: 由式(9.13)及条件式(2)得 则 ,即系统满足初始条件。 I C B Γ t t t 1 x x y y k 0 1, 2,3, , 0 0 0 0 d k k y y k t t d t T 0, y Cx Cx y k k k k 1 1 0 0 0 0 ek 0 0 0,1, 2, k 非齐次一阶线性微分方程 的解为: 取 ,则 由于 , ,则 x A x B u t t t t t 0 0 0 0 0 0 exp d exp d exp d d exp exp exp d exp exp d t t t t t t t t t t x C A A B u A C A A B u A C A A B u Φ A t t , exp 1 1 0 , d t k k k k t t t x x Φ B u u d e y y k k t t t 1 d 1 e y y k k t t t 1 1 1 1 0 , d e e y y C x x C Φ B u u k k k k k k t k k t t t t t t t t t 即 将PID型控制律式(9.14)代入上式,则第k+1次输出的误差为: (9.15) 利用分部积分公式,令 ,有 (9.16) 将式(9.16)代入式(9.15),得 (9.17) 1 1 0 e e C Φ B u u , d t k k k k t t t t 1 0 0 e e C Φ B Γ e L e Ψ e , d d t k k k k k t t t t G C B Γ t t , 0 0 0 0 d , , d , d t t t k k k t k k t t t t t C B Γ e G e G e C B Γ e G e 1 0 0 0 0 , d , d , d d e I C B Γ e G e C Φ B L e C Φ B ψ e t k k k t t k k t t t t t t t t t t 将式(9.17)两端取范数,有 (9.18) 式中 根据 范数的定义可知,函数 的范数为 。 将式(9.18)两端同乘以 , ,并考虑到 有 1 0 0 0 0 1 2 0 0 0 , d , d , d d d d d e I C B Γ e G e C Φ B L e C Φ B ψ e I C B Γ e e e t k k k t t k k t t k k k t t t t t t t t t t t t t t b b 1 , 0, , 0, max sup , , sup , t T t T b t t t G C Φ B L 2 , 0, sup , C Φ B ψ t T b t t : 0, n f T R 0 sup e t t T f f t expt 0 0 exp 1 exp d t t (9.19) 根据 范数的定义,函数 的范数为: 由于 , , ,则有 。 将式(9.19)的结果应用于下式,得: 1 1 1 0 0 0 1 1 1 1 exp d exp exp exp d exp exp d exp 1 1 exp exp exp exp 1 1 exp t t t k k k k k k k t b t b b t t b t b t t t b T b e e e e e e e : 0, n f T R 0 sup t t T f f t e t T 0, 0,t 0, k k e e

ap(-)Chb.(olldad:mp(-)fcoplar)ep(-4r)['h (oladn 测(919)和(9.20)代入(9.18),得 且53每真实南 sam-wf-pi6上-4ol+r kL≤L (9.21) 考意2地入着出黄性纯 6上-e-p-om(啡.e出 其中4于可于,则当a取是够大时,可以 A上a-边p啡.rlm 使户c因此巴礼0,定理得证 如果将控制律式(914)中的政为+身则为闭环种D型选代学 aa-pl-啡.el即 [ET网 习控制律,同定理1的证明过程,可证明闭环和D选代学习控制律, 颗恒咖为 6上4.t上出ヅet 其中。e--s-p-, [C时但周 r-[fsb.(pc(-b.c (9.20) 由干司,取-”可满足定理1中的条件(1),在空制牌 式(9.1d)中取已习6系绕的初始枝态为他得 在chp92sim.md定序中,选择Simulink的Manual Switch开关,将开 关向下,取PD型开环达代学习控制撑,竹真结果见图94至96所示。 将开关向上,采周PD型闭环选代学习控制律,仿真结果见图的7至99 a3 所示,可见,闭环收敛速度好于开环收速度 可43功次选代单习的眼雕过细 回3-5第30汝造代攀习的业桌 黎(杯中D拉) 5
5 其中 。 即 (9.20) 2 2 0 0 0 0 2 0 2 0 2 0 2 2 exp d d exp exp exp d d 1 exp exp exp d 1 exp exp exp d 1 exp exp exp d 1 exp exp 1 exp 1 exp 1 ex t t k k t k t k t k k k t b t b T t b T b t T b t T t b t T b e e e e e e e 2 2 p 1 exp k t T b e 1 exp 1 exp 0 t T 2 2 2 0 0 1 exp exp d d t k k T t b b e e 则(9.19)和(9.20)代入(9.18),得 (9.21) 其中 。由于 ,则当 取足够大时,可以 使 。 因此 。定理得证。 如果将控制律式(9.14)中的 改为 ,则为闭环PID型迭代学 习控制律。同定理1的证明过程,可证明闭环PID迭代学习控制律。 1 e e k k 2 1 2 1 exp 1 exp T T b b 1 1 lim 0 ek k ek ek 1 9.5.3 仿真实例 考虑2输入2输出线性系统: 期望跟踪轨迹为 1 1 1 2 2 2 2 3 1 1 1 1 0 1 x t x t u t x t x t u t 1 1 2 2 2 0 0 1 y t x t y t x t 1d 2d sin(3 ) cos(3 ) y t t y t t t 0,1 由于 ,取 ,可满足定理1中的条件(1),在控制律 式(9.14)中取 , ,系统的初始状态为 。 在chap9_2sim.mdl程序中,选择Simulink的Manual Switch开关,将开 关向下,取PD型开环迭代学习控制律,仿真结果见图9-4至9-6所示。 将开关向上,采用PD型闭环迭代学习控制律,仿真结果见图9-7至9-9 所示。可见,闭环收敛速度好于开环收敛速度。 2 2 0 1 CB 0.95 0 0 0.95 Γ 2.0 0 0 2.0 L Ψ 0 1 0 2 0 0 0 0 1 x x 图9-4 30次迭代学习的跟踪过程 (开环PD控制) 图9-5 第30次迭代学习的位置跟 踪(开环PD控制)
05句 04 06 02 04 1m ■960次地代过圆中跳量大地对惟 02 04 的收草过开P心控初 04 06 08 ime约 圆9730次进代学习的厘过看 国日山第卫0沈选代津习的位厚 章(坏PDD Chenge of naonun adue wh时o时eat ard eeo7Mhrs 3.后亭路京磨人钠淀厚厚透代养习地制 9.6.1量达璃 移动肌疆人是一州在复来的环黄下工作的具有查、自■帆、自 ?代表N单咏民空间,克文南量海为: 藏应童力的肌人,在客动肌整人的湘关战术新汽中,数批术是关 H-e (9.2 其中工 旅心故木,也是其实桌其正的帽管化和亮业的自主落动的关脑故术, C▣一为剂Pm前实兼短弃,定义见序直重为 事动小是人具有时交、童铜杏有的性的动力学物恒由于到量水建 ICHcc) (9.2均 模的不着南。加上负铁的定化以及外算找动的纳,失你上无法得调 其中见日冠麻的量大物植, 移播人精南、整的功视业, 度化石:定义意为 重过女2刀的业方注进行弹细维导及你高分桥,究一我动机 4Lp4目.24→e (9,24 叠人地代学习高散性铺的提计及仿真方法, 6
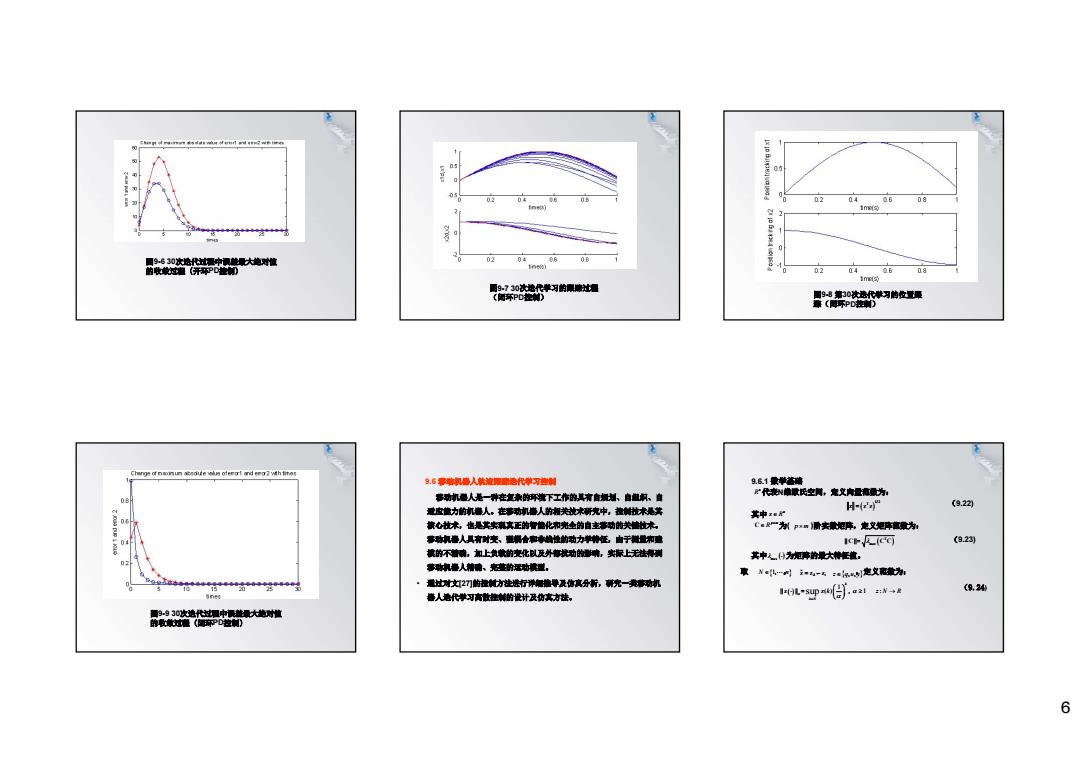
6 图9-6 30次迭代过程中误差最大绝对值 的收敛过程(开环PD控制) 图9-7 30次迭代学习的跟踪过程 (闭环PD控制) 图9-8 第30次迭代学习的位置跟 踪(闭环PD控制) 图9-9 30次迭代过程中误差最大绝对值 的收敛过程(闭环PD控制) 9.6 移动机器人轨迹跟踪迭代学习控制 移动机器人是一种在复杂的环境下工作的具有自规划、自组织、自 适应能力的机器人。在移动机器人的相关技术研究中,控制技术是其 核心技术,也是其实现真正的智能化和完全的自主移动的关键技术。 移动机器人具有时变、强耦合和非线性的动力学特征,由于测量和建 模的不精确,加上负载的变化以及外部扰动的影响,实际上无法得到 移动机器人精确、完整的运动模型。 • 通过对文[27]的控制方法进行详细推导及仿真分析,研究一类移动机 器人迭代学习离散控制的设计及仿真方法。 9.6.1 数学基础 代表N维欧氏空间,定义向量范数为: (9.22) 其中 为( )阶实数矩阵,定义矩阵范数为: (9.23) 其中 为矩阵的最大特征值。 取 , , ,定义范数为: (9.24) n R 1/ 2 T z z z n z R p m R C p m T || || C C C max max N n 1, , d i z z z z q u y , , 1 || || ( ) , 1 sup k k N k z z z N R :

962系规槽述 极据图职10,针对P点,移动城器人的离敬运动学方程可由下式描选 9RP. 图910为移动机器人运动模型,它在同一极触上有两个独立的推进轮 ,机器人在二排空间移动,点代有机指人的当前位置。广义坐标定义 树 925 为,和为直角坐标系下的坐标,为机器人的方位角。当机器人的标定 方向为地理坐标采的横触正半触时,定文为0。移动机情人受不完全 其中A为采样时间,机器人获态向量为-5,心可,速度 约束的影响而只能在臣动轮轴的方向运动,点的线速度和角速度定义 向量为气,传一,· 为和 式(925)可写为: t+-)+倒甲,肉 (9.26) 其中 同910警动机最人视过 「m的门 (927) 如图910听示,期里轨迹为心心。1x上sm运动输迹 在动机器人横数 具中为状态干扰,)为缩出测量噪声,)国.,为系统 动态的制器 翠年的控制问避就是为确定出一kk开使诺弃男4 输出,-r好 线速度和角速度误差分别为: -[5,了 考虑选代过程.由(930)和(9.31)可得 )5- (9.28 q4k+-q+围4使+k使以 (9.32 ,4-到 (9.29) )=+) (9.33 移动机人选代学习控制系统轴构如图的11所示。 图丝行等南肌量人进代学习控响原球销物 其中,为选代次数,为离散时间,kl因因 事射讯最人高批方可辅站★下: 分别代表第次选代的状态,编入。输出、状态干找和输出噪声。 k+=+到军,k)+倒k (9.30 机器人运动方程(9.32)和(9.33)满足下列性质和假设: (9.3i 性质1:考虑旺想情况。取化%,均为零,k=N,则期亚轨迹的方程 可写为 见传+与=电+倒包国, (934) - (9.35) 7
7 9.6.2 系统描述 图9-10为移动机器人运动模型,它在同一根轴上有两个独立的推进轮 ,机器人在二维空间移动,点代表机器人的当前位置,广义坐标定义 为,和为直角坐标系下的坐标,为机器人的方位角。当机器人的标定 方向为地理坐标系的横轴正半轴时,定义为0。移动机器人受不完全 约束的影响而只能在驱动轮轴的方向运动,点的线速度和角速度定义 为和。 图9-10 移动机器人运动模型 根据图9-10,针对P点,移动机器人的离散运动学方程可由下式描述 • (9.25) 其中 为采样时间,机器人状态向量为 ,速度 向量为 。 式(9.25)可写为: (9.26) 其中 • (9.27) p p p p p p p p p p ( 1) ( ) cos ( ) 0 ( ) ( 1) ( ) sin ( ) 0 ( ) ( 1) ( ) 0 1 x k x k k v k y k y k T k k k k T T p p p ( ) ( ), ( ), ( ) k x k y k k q T p p p ( ) ( ), ( ) k v k k u p q q B q u ( 1) ( ) ( ( ), ) ( ) k k k k k p p p cos ( ) 0 ( ( ), ) sin ( ) 0 0 1 k k k T k B q 如图9-10所示,期望轨迹为 。运动轨迹 跟踪的控制问题就是为确定 ,使 跟踪 。 线速度和角速度误差分别为: (9.28) (9.29) 移动机器人迭代学习控制系统结构如图9-11所示。 pd d d d ( ) ( ), ( ), ( ) , 1 k x k y k k k n T u( ) ( ), ( ) k v k k P k( ) d P k( ) v k v k v k p p ( ) ( ) ( ) k k k 图9-11 移动机器人迭代学习控制系统结构 移动机器人离散运动学方程可描述如下: (9.30) (9.31) q q B q u ( 1) ( ) ( ( ), ) ( ) ( ), k k k k k k β y q ( ) ( ) ( ) k k k γ 其中 为状态干扰, 为输出测量噪声, 为系统 输出, 。 考虑迭代过程,由(9.30)和(9.31)可得: (9.32) (9.33) 其中 为迭代次数, 为离散时间, 。 , 分别代表第 次迭代的状态、输入、输出、状态干扰和输出噪声。 机器人运动方程(9.32)和(9.33)满足下列性质和假设: 性质1:考虑理想情况,取 均为零, ,则期望轨迹的方程 可写为 (9.34) (9.35) β( ) k γ( ) k T y( ) ( ), ( ), ( ) k x k y k k ( ) ( ), ( ) k v k k T u ( 1) ( ) ( ( ), ) ( ) ( ), i i i i i q q B q u β k k k k k k ( ) ( ) ( ) i i i y q γ k k k i k k n 1, , ( ) i q k ( ), ( ), ( ), ( ) i i i i u y β γ k k k k i ( ), ( ) i i β γ k k k N d d d d q q B u ( 1) ( ) (q ( ), ) ( ), k k k k k d d y q ( ) ( ), k k

性质2:矩骑通数满足Lp5c小iz条件: 9.B3控制健设计及收数性分析 定11考德高散减能(9.32)咖(但.33),演是量设13,采则挂 1k小断非,4-·k.N,G为正常数 (9.3) 选代学习控制檬设计为: 律(9.38), 性质子:矩骑脚aL与是有界的L啡A内正常数,矩骑断气 黑=+Lk,达+与+L (9.38) l-L使qkkP4气>0· 、桌产0调增的存在,则I-®因目,白-川,.-y4明 假设2:干扰和降声有界 通过控刺律(9.3》,使状态变量。队、控制输入系统编出, 分别收敛于期圣值. 有界,具收敏于一4及的圆量。 恶联体器照4体与(9.37刀 正: 其中鸟,4为正常数。 由式(9.340和(92)01 假设3:在每一次选代中,缺迹都是从。,向的邻城开始,即 14物-0形气,430,21· 4+-飞使+-气+与 ·由(9.38)式得: 传+倒因马周内+叫.内+ 利用性质2和假设2得 -因-副4,-时国,[✉四-s因+厅k国 -4内-[气-断严+倒因内-) (940) b-- --Lg使+-L以ke的 的电-LW换4气sh 考虑性质2和3及假设1和2,得 -1ky+-y+-b- +气,,++气,鸟 ke-nshetsh -A-1k+与-气t+-+-l,4k-A-了使订 令4-气,+人=生点与A,6++与则 -色-L圳k+副k-g因-g 令41+k.,则 4L6+k+可-1,k4-7k+明 色-LAA因气,A4 A+与南4色 =-k-lLk[围o4台-到q4a-+] 将(9.39)和(9.41)代入上式,得 ++-与+可 对上式进行递推并考虑假设3,得: --k地-Lk商气d填-k可到q-Bg中 b水内店一w小6] ka啡营kU小 (941) -Lk片+L服4+4W+Ln因 --离q,片k)-Lk元-倒q-到4wd [2一小小4 -L片+BA+T+L打( 8
8 性质2:矩阵函数满足Lipschitz条件: , , 为正常数 (9.36) 性质3:矩阵 是有界的 , ,为正常数,矩阵 为 的满秩矩阵。 假设1: ; 假设2:干扰和噪声有界 (9.37) 其中 , 为正常数。 假设3:在每一次迭代中,轨迹都是从 的邻域开始,即 , , 。 1 2 B 1 2 || ( , ) ( , ) || || || B q B q q q k k c k N B c ( ( ), ) i B q k k B || ( ( ), ) || i B q k k b ( ( ), ) i B q k k ( ( ), ) i q k k d ud 1 max || ( ) || k n k b u 1 1 k n 1 1 k n max max || ( ) || , max max || ( ) || i i i i k b k b β γ b b d q (0) 0 d q || (0) (0) || i q q b 0 q b 0 i 1 9.6.3 控制律设计及收敛性分析 迭代学习控制律设计为: (9.38) 对于第i次迭代,跟踪误差信号为 , 和 为学习 的增益矩阵,满足 , , , , 。 通过控制律(9.38),使状态变量 、控制输入 、系统输出 分别收敛于期望值。 1 1 2 1 ( ) ( ) ( ) ( 1) ( ) ( ) i i i i k k k k k k u u L e L e d ( ) ( ) ( ) i i e y y k k k 1 L ( ) k 2 L ( ) k 1 1 L || ( ) || L k b 2 2 L || ( ) || L k b k N L1 b 0 L2 b 0 ( ) i q k ( ) i u k ( ) i y k 定理 1:考虑离散系统(9.32)和(9.33),满足假设1-3,采用控 制律(9.38),则 (9.39) 对于所有 都成立。如果忽略状态干扰,输出噪声和初始 状态误差(即 ),则分别收敛于期望值。如果考虑干扰 、噪声和误差的存在,则 , , 有界,且收敛于 的函数。 证明: 由式(9.34)和(9.32)得: 1 || ( ) ( , ) || 1 i I L B q k k ( , ) n i q k R N 0 q b b b 0 d || ( ) ( ) ||| i u u k k d || ( ) ( ) || i q q k k d || ( ) ( ) || i y y k k 0 q b b b , , (9.40) 考虑性质2和3及假设1和2,得 令 ,则 对上式进行递推并考虑假设3,得: (9.41) d d d d d d d d d d 1 1 1 , , , , , , , i i i i i i i i i i i i i i i k k k k k k k k k k k k k k k k q k k k k k k k k k k k k k k k k q q q q B q u q B q u β q B q u B u u u β q B q B q u B q u β B u B d 1 i i i i k k c b k b k b q q q u d 2 B u h c b 1 q q u i i i k h k b k b 1 2 B 0 1 1 2 B 2 q 0 k k j k i i j k h b j b h b q u • 由(9.38)式得: 1 d 1 d 1 2 1 1 d 2 d 1 1 d 2 d 1 1 1 d d ( ) ( ) ( ) ( ) ( ) ( ) ( 1) ( ) ( ) ( ) ( ) ( 1) ( 1) ( ) ( ) ( ) ( ) ( ) ( 1) ( 1) ( 1) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ( ), ) i i i i i i i i i i i i i i k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k u u u u u L e L e u L y y L y y u L q q γ L q q γ u L q B q u d 1 2 1 1 1 1 d d d d 1 1 2 1 1 1 ( ) ( ) ( ( ), ) ( ) ( ) ( ) ( 1) ( ) ( ) ( 1) ( ) ( ) ( ) ( ) ( ( ), ) ( ) ( ( ), ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( 1) ( ) ( i i i i i i i i i i i i i i i i k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k k q B q u L β γ L q γ u L q L B q u B q u u u L β γ L q γ u L 1 1 d d 2 1 1 1 2 1 1 1 1 d d 2 1 1 ) ( ) ( ) ( ( ), ) ( ) ( ) ( ( ), ) ( ( ), ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ( ), ) ( ) ( ) ( ) ( ) ( ( ), ) ( ( ), ) ( ) ( ) ( ) ( ) i i i i i i i i i i i i i k k k k k k k k q k k k k k k k k k k k k k k k k k k k k k k k k k q L B q u L B q B u L q L β γ L γ I L B q u L q L B q B q u L q L β 1 2 1 ( ) ( ) ( ) ( ) i i i k k k k γ L γ 利用性质2和假设2,得 令 , ,则 将(9.39)和(9.41)代入上式,得 1 1 d 2 1 2 1 1 L L B u L 1 L L ( ) ( ) ( ( ), ) ( ) ( ) ( ) ( ) ( ) i i i i i i k k k k k b k b c b k b k b b b b b u I L B q u q q q 1 d 1 1 L B u L 2 h b c b b h (1 ) 1 2 1 L L b b b b b b ( ) 2 1 1 1 L 1 1 ( ) ( ) ( ( ), ) ( ) ( ) ( ) i i i i i k k k k k h k b k b u I L B q u q q 0 2 0 1 1 1 1 2 B 2 0 1 1 L 2 B 1 2 q 1 0 ( ) ( ) ( ) ( ) k k j k i i i q j k k j k i j k k h h b j b h b b h b j b h b b u u u u

因此 ·取>m.得 A啡传+情芝g飘] 4芝g[s5w] LL4L信[广 -hg}lwlaa 上式两请问第,取范数,得 e +4f-传 礼性 其中。积据等比戴列有 +】 色广u l色tr 广非 (9.43) -4 侣w町 M 但er.兴 (a%- -鸟 +-a] ·kl ·令a>4A+4h】·则(《942)变为 ·同理.(941)式两璃问时乘以,得 ·将(9.35式减(9.33的式.得 5,)y,-无--)+-4-因 L≤L (944) w ·将上式两端问时乘以得到 ·其中w2兰 4兴 由于日=4.点1,并利用(943)式.得 F.LsAL+4 w要 人M'a ·将(9.46)代入上式,得 0与 lAL+6卢e线-A5L6,g6 g-鸟 ·对(944)式进行递推,得 ·将式(945⑤代入上式裤 =5La-e告4-aA49m -1- g息 pl:hl.vpl ---9+-i-(9.46) ·由(9.45)·(9.47)式,可得结论为:当5@4人种。L ·取▣足够大,使sP<1,可得 ·将(9.3式减(9.33试,得 ·,L,L收做于零,否测LhLL.接基于4人的数有 界收欲。 4六 (9.45) )--(-(-+切--元) 9
9 因此 上式两端同乘,取范数,得 2 0 2 1 1 1 1 2 1 1 2 B 0 1 1 L 2 B 1 0 ( ) ( ) ( ) ( ) k k k j i i L q i j k k j i j k k h b h b b h h b j b b h b j b u u u u 2 0 2 2 1 1 L q 1 1 1 2 1 B 0 1 1 L 2 B 1 0 1 1 ( ) ( ) ( ) 1 1 1 ( ) 1 1 ( ) k k k i i k j j k j k i j k j j k i j h k k h b b h h b b j b b h b j b u u u u j • 取 ,得 max 1, h2 2 0 2 2 0 2 1 1 1 2 1 1 q 1 B 0 1 1 L 2 B 1 0 1 2 1 q 1 B 2 L 2 B 1 ( ) ( ) 1 / ( ) ( ) 1 / ( ) k j k i i L i j k j k i j n i L i n i h h h b b b b b b h b b h h h b b b b b h b h b b u u u u u u u 2 2 0 2 2 2 2 B 1 B L 1 1 L q 1 2 2 1 L 2 2 1 / 1 / | ( ) 1 / n n i i n h h h b h b b h b b b h h b h b h h u u 即 (9.42) 其中,根据等比数列有 (9.43) • 。 2 2 0 2 2 2 B L 1 B 1 1 L q 1 2 2 1 L 2 2 1 / 1 / 1 ( ) 1 / n n i i n h h b b b h h b b b h h b h b h h u u 1 1 1 1 1 1 2 2 2 2 0 0 0 2 1 1 2 2 2 2 2 2 2 2 2 2 1 1 1 1 1 / ( / ) 1 1 / 1 / / 1 1 j k j k j k k k k j j j k k k k k n h h h h h h h h h h h h h h h k n 1, , • 令 ,则(9.42)变为 • (9.44) • 其中 。 • 对(9.44)式进行递推,得 • 取 足够大 ,使 ,可得 • (9.45) max 1, , h h b b 2 2 B L2 1 ˆ i i u u 2 2 B 1 2 2 B L 2 1 / ˆ 1 / 1 n n h b h h h b b h 2 0 2 2 1 L q 1 2 2 B L 2 1 / ( ) 1 / 1 n n h h b b b b h h b b h 1 1 1 1 0 (1 ) ˆ ˆ ˆ ˆ 1 ˆ i i i j i i j u u u ˆ 1 lim || || 1 ˆ i i u • 同理, (9.41)式两端同时乘以,得 • 由于 , ,并利用(9.43)式,得 • 将式(9.45)代入上式,得 • (9.46) • 将(9.35)式减(9.33)式,得 0 1 1 2 2 B q 0 1 1 1 1 | ( ) ( ) k j j k j k k i i j h h k b j b b q u 1 j b b 2 1 h 0 0 2 2 2 B q B q 2 2 2 1 / 1 / 1 / n n n i i i h h h b b b b b b h h h q u u y y y q q γ q γ i i i i i i k k k k k k k k d d ( ) ( ) ( ) y y y q q γ q γ i i i i i i k k k k k k k k d d ( ) ( ) ( ) • 将(9.35)式减(9.33)式,得 • 将上式两端同时乘以得到 • 将(9.46)代入上式,得 • (9.47) • 由(9.45)-(9.47)式,可得结论为:当 时, • , , 收敛于零,否则 , , ,按基于 的函数有 界收敛。 y y y q q γ q γ i i i i i i k k k k k k k k d d ( ) ( ) ( ) i i b y q 0 2 2 B q 2 2 1 / 1 / lim 1 ˆ n n i i h h b b b b h h y 0 q b b b 0, 0, 0 i u i q i y i u i q i y 0 q b b b , ,
·9.84伪真实例 。 针对移动机器人离散系统(9.32)和(9.33),年次选代被控对象 初始值与理想结号初始值相可,即取网-心0一0 6间一0其中w@m心向第欢达代时的切始状态, 。采用选代学习控制律(9.3翅》,位直指令为)9e 化)世+三。按收做条件(939),取控制器的嫩益矩阵为 a 05 采样时间为a7,®001,取选代次数为500次,每次选代时间为 2000次.仿真结果知图912至图914所示. 国912直造代次单运功铁连的海家过定 国93最后一次的位毫 厨914院选代次量的收教过据 10
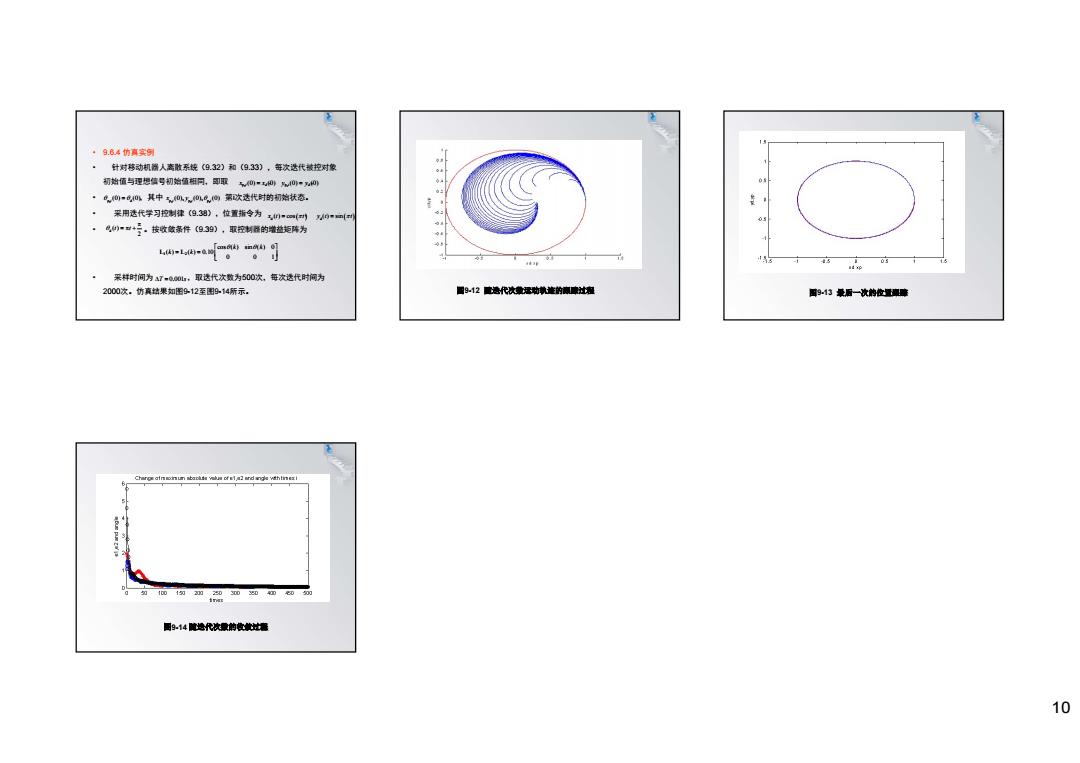
10 • 9.6.4 仿真实例 • 针对移动机器人离散系统(9.32)和(9.33),每次迭代被控对象 初始值与理想信号初始值相同,即取 , , • ,其中 第i次迭代时的初始状态。 • 采用迭代学习控制律(9.38),位置指令为 , • 。按收敛条件(9.39),取控制器的增益矩阵为 • 采样时间为 ,取迭代次数为500次,每次迭代时间为 2000次。仿真结果如图9-12至图9-14所示。 p, d (0) (0) i x x p, d (0) (0) i y y p, d (0) (0) i p, p, p, (0), (0), (0) i i i x y x t t d ( ) cos y t t d ( ) sin d π ( ) π 2 t t 1 2 cos ( ) sin ( ) 0 ( ) ( ) 0.10 0 0 1 k k k k L L T s 0.001 图9-12 随迭代次数运动轨迹的跟踪过程 图9-13 最后一次的位置跟踪 图9-14 随迭代次数的收敛过程