
多机系统的静态稳定近似分析 一、简化和近似 由前几节对单机无穷大系统的静态稳定性分析可 知,如果要计及各种对发电机的影响因素(机械 阻力,电磁阻尼,励磁调节,电磁暂态过程), 即使是一台发电机也是相当复杂的。 。实际的系统中发电机台数很多,在工程计算中往 往采用一些简化的措施:
多机系统的静态稳定近似分析 一、简化和近似 由前几节对单机无穷大系统的静态稳定性分析可 知,如果要计及各种对发电机的影响因素(机械 阻力,电磁阻尼,励磁调节,电磁暂态过程), 即使是一台发电机也是相当复杂的。 实际的系统中发电机台数很多,在工程计算中往 往采用一些简化的措施:

① 对发电机进行简化 第一步:简化励磁调节的作用,认为E,为常数; 对励磁调节简化,假设励磁参数选择适当,不会引起系统失稳, 这时把发电机看作一个有恒定暂态电动势E,的电源, 不再计及调节器的影响。 第二步:为了方便计算,将E,恒定近似认为E恒定 为了计算方便,在工程实际中近似地认为发电机暂态电抗后的 电动势E'为常数 这样就将发电机简化为一个有恒定电动势E',内电抗为x,的电源

② 对负荷的近似处理 恒定阻抗模型Z,=R+X [Mw=k[a+(1-a)(1-sy] a会心c U'r. 2w 静态负荷模型 [P=a,+b,U+p,静态负荷=恒阻抗+恒电流+恒功率 Q=aU2+bU+c 综合负荷= 静态负荷 +电动机负荷 ↑ ↑ (功率与U,f成某一固定函数, (微分方程描述动态元件出现 不存在稳定问题) 扰动时,可能失稳) 为了近似计算,负荷以恒定阻抗来代表
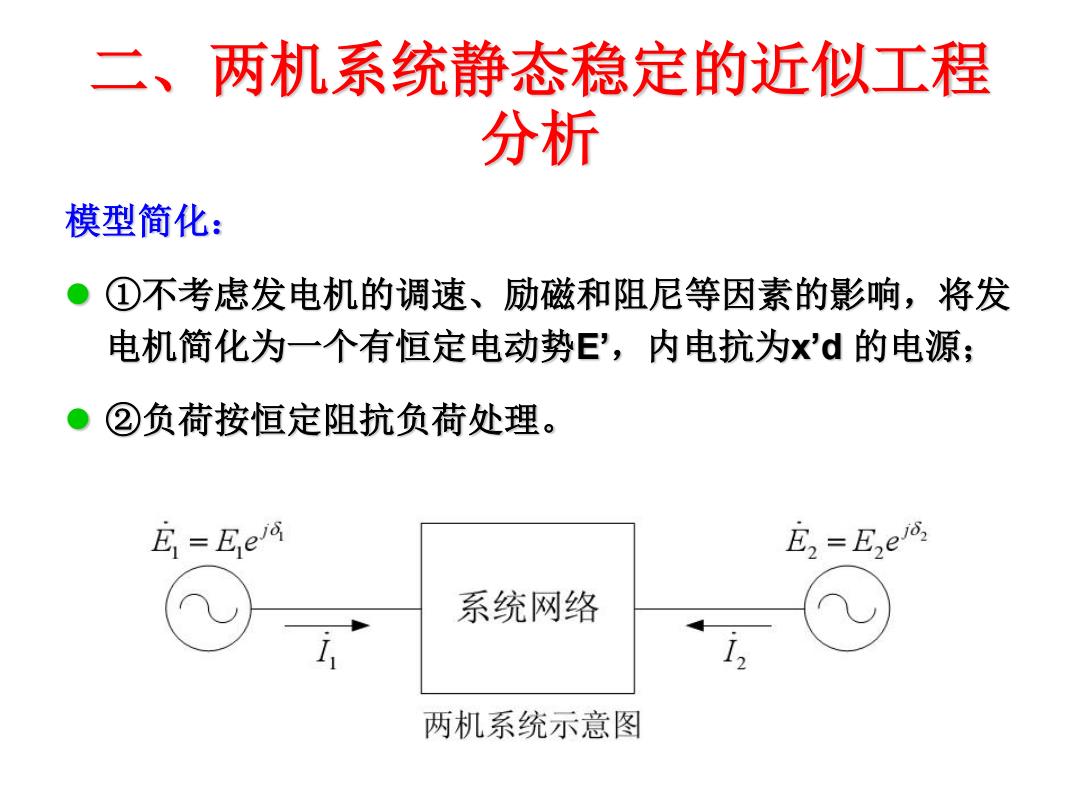
二、两机系统静态稳定的近似工程 分析 模型简化: ①不考虑发电机的调速、励磁和阻尼等因素的影响,将发 电机简化为一个有恒定电动势E',内电抗为x'd的电源; ②负荷按恒定阻抗负荷处理。 E=Ee 系统网络 1 两机系统示意图
二、两机系统静态稳定的近似工程 分析 模型简化: ①不考虑发电机的调速、励磁和阻尼等因素的影响,将发 电机简化为一个有恒定电动势E’,内电抗为x’d 的电源; ②负荷按恒定阻抗负荷处理
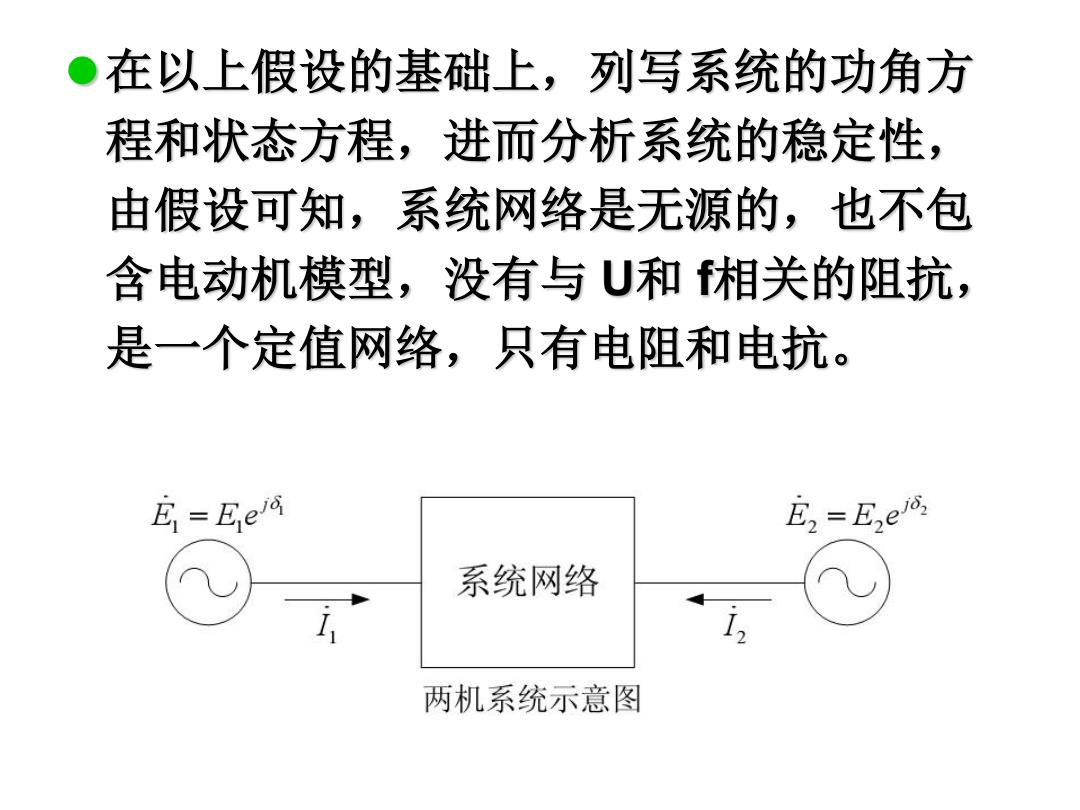
●在以上假设的基础上,列写系统的功角方 程和状态方程,进而分析系统的稳定性, 由假设可知,系统网络是无源的,也不包 含电动机模型,没有与U和相关的阻抗, 是一个定值网络,只有电阻和电抗。 E=Ee E2=Ee 系统网络 11 两机系统示意图
在以上假设的基础上,列写系统的功角方 程和状态方程,进而分析系统的稳定性, 由假设可知,系统网络是无源的,也不包 含电动机模型,没有与 U和 f相关的阻抗, 是一个定值网络,只有电阻和电抗
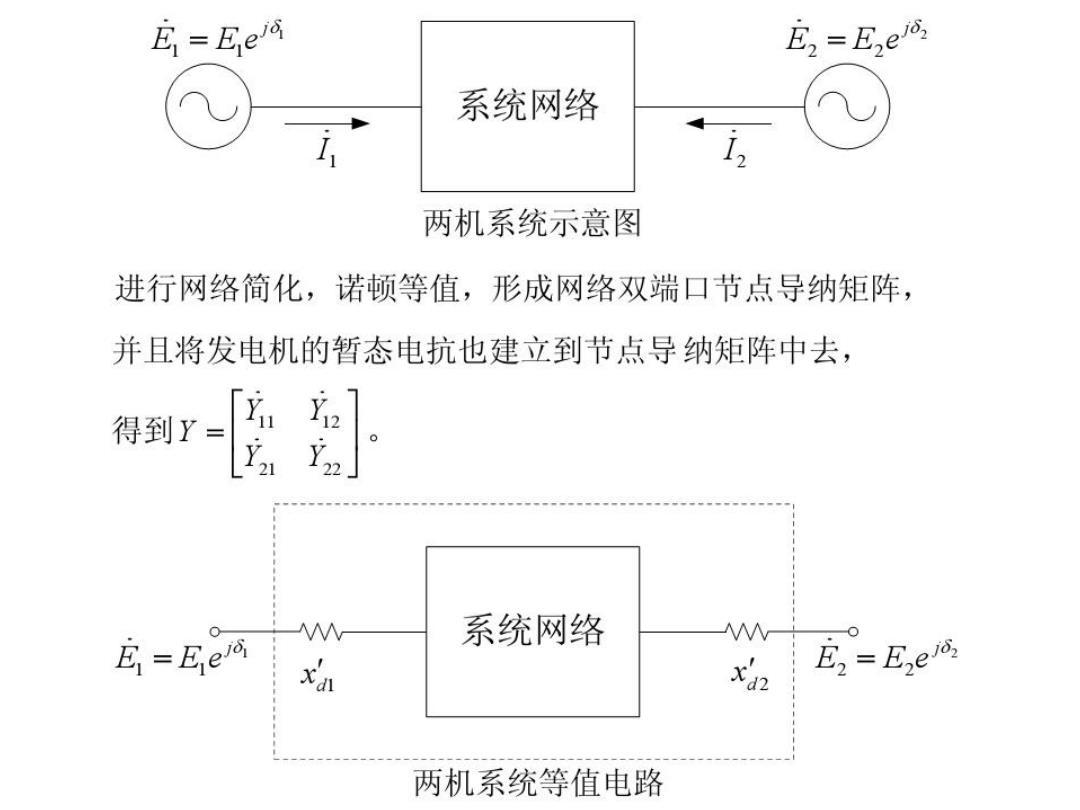
E=Ee E2=Eel6 系统网络 两机系统示意图 进行网络简化,诺顿等值,形成网络双端口节点导纳矩阵, 并且将发电机的暂态电抗也建立到节点导纳矩阵中去, 得到Y= 2 W 系统网络 =Ee E2 =Ezelo. 两机系统等值电路
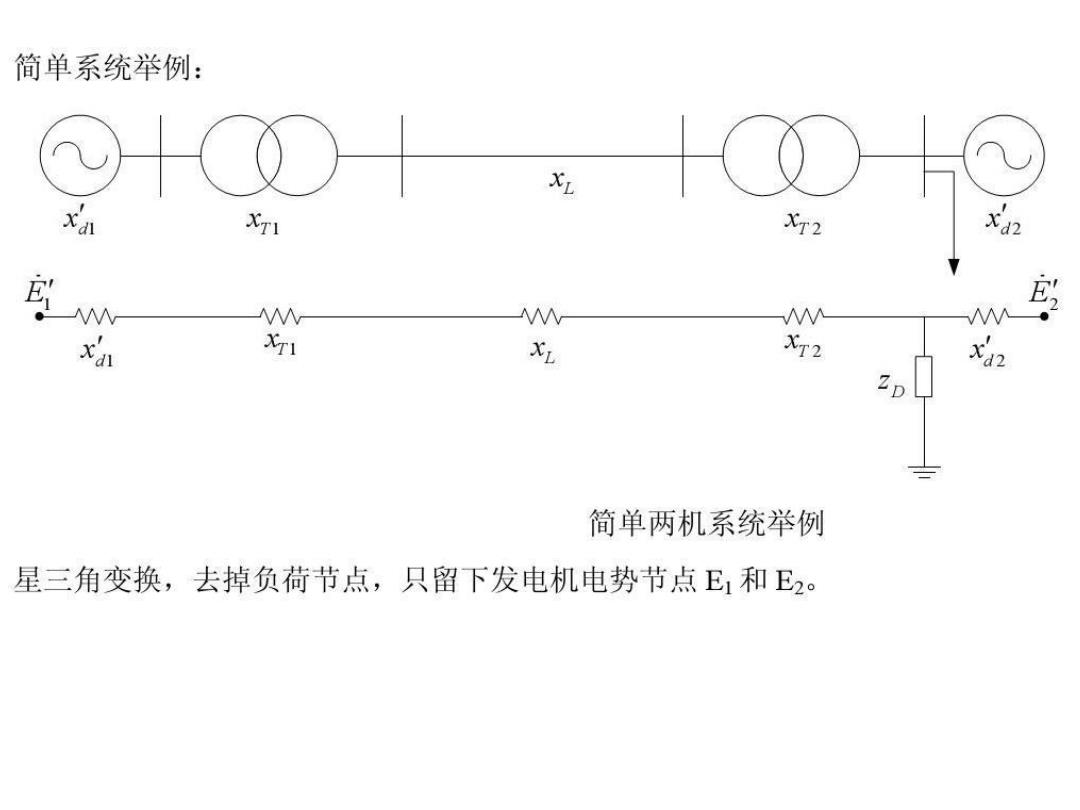
简单系统举例: XL XT2 W sa 1 XL XT2 简单两机系统举例 星三角变换,去掉负荷节点,只留下发电机电势节点E和E2

第一步:列写电磁功率与电压和角度的关系方程: P=U,∑U,(G,cos8,+B,sin8) 由潮流方程 9,=U,∑,(G,sin6,-B,cos0,) 可得两机系统各台发电机的输出功率为: P =EGu+EE2 (B2 sin 2 +G2 cos 2) PE,=E2G2+EYE2 (-B2 sin 2 +G2 cos 2) 表明发电机的电磁功率是相对角62的函数。 x XTI XT2 N W sa 1 XL XT2
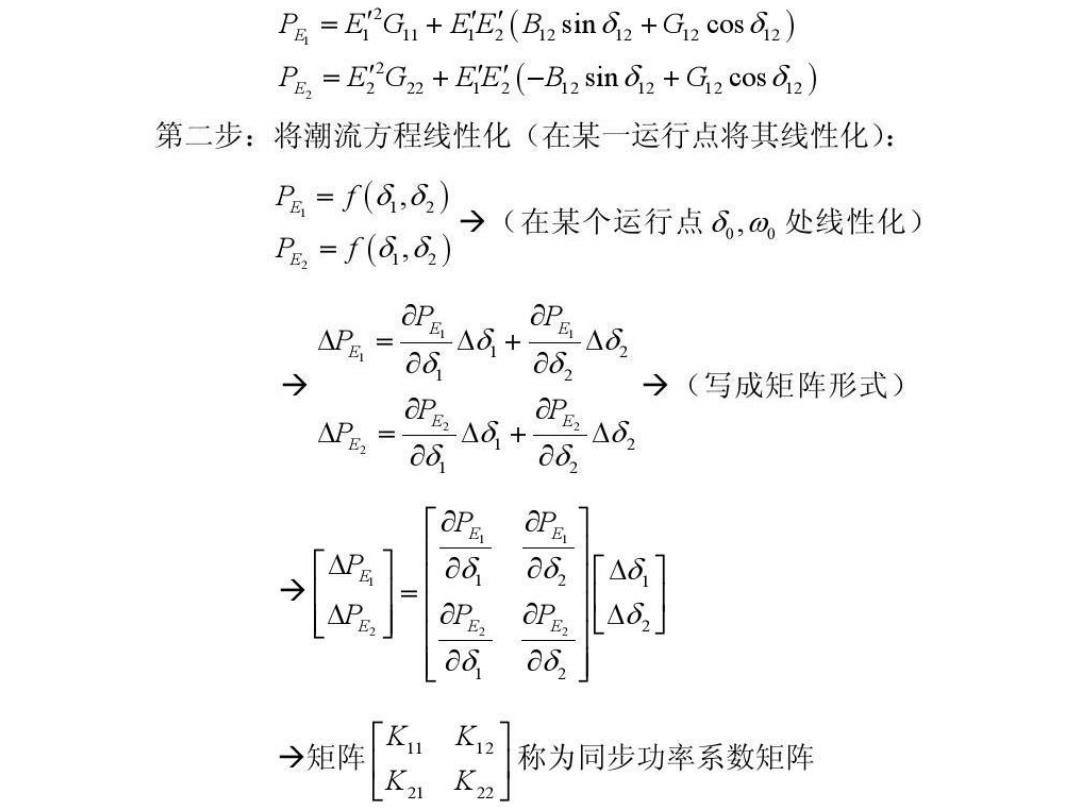
PE =EGu+EE2 (B2 sin 2 +G2 cos 2) PE,=E2G22 +EE2 (-B2 sin 2 +G2 cos2) 第二步:将潮流方程线性化(在某一运行点将其线性化): P=f(d,8)) (在某个运行点6,@,处线性化) P.=f(8.82) P6,*aδ APE OPE2 → →(写成矩阵形式) P, P2δn P2A6+0δ OPE → a a6, OPE: a62 →矩阵 「K 称为同步功率系数矩阵 Ka
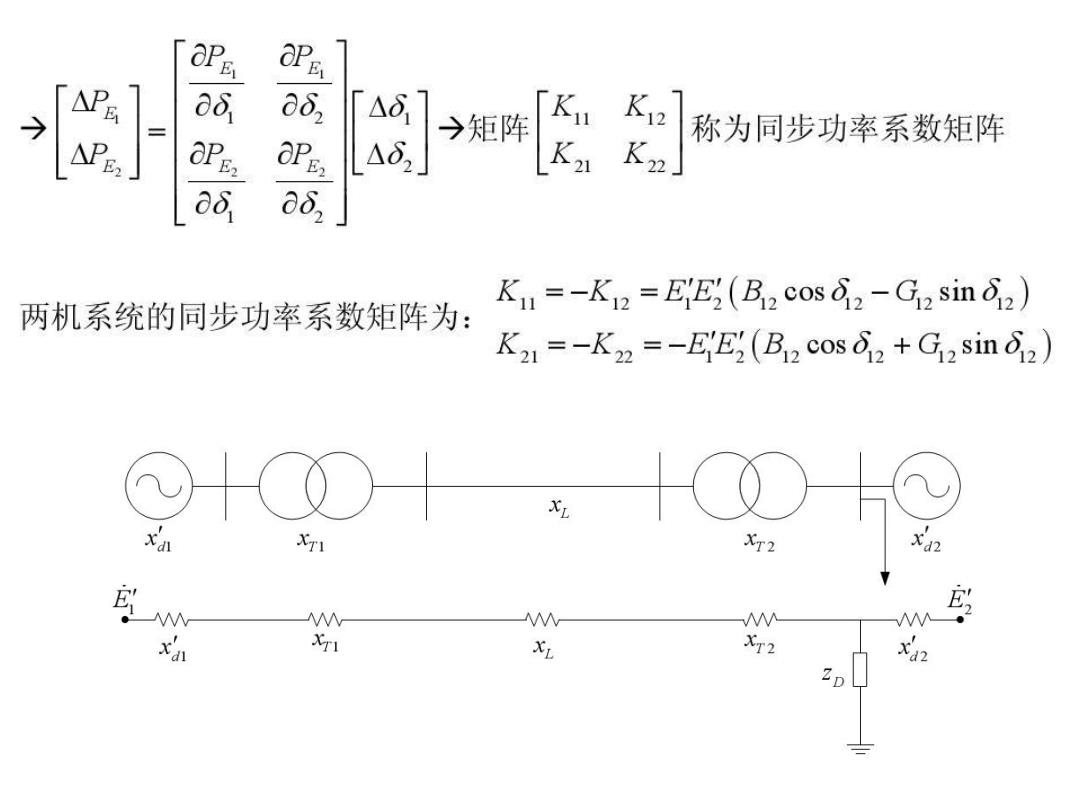
→ →矩阵 称为同步功率系数矩阵 Kn Ku=-K12=EE2(B2 COS 2-G2 sin 2) 两机系统的同步功率系数矩阵为: K21=-K22=-EE2 (B2 cos 2+G2 sin 2) ⊙+C 的 W W W XTI x XT2