
简单电力系统的静态稳定 一、静态稳定性定义 电力系统静态稳定的基本概念: 电力系统受到小干扰后,不发生自发性振荡或非周期性失步, 起因 条件 自动恢复到初始运行状态的能力。 结果 研究内容 也就是说,电力系统静态稳定是电力系统的某种能力: 简单地说,就是指电力系统受到小干扰时维持同步运行状态的能力。 也可以将静态稳定问题理解为确定系统的某个运行稳态能否保持的问题
简单电力系统的静态稳定

小干扰的类型: 负荷的小量变化: 架空输电线因风吹摆动引起的线间距离的微小变化: 气温或气压引起某个参数的变化: 汽轮机蒸汽压力的波动; 发电机端电压发生小的偏移: 等

小干扰的持续性:干扰可能是瞬时性的,也可能是永久性的。 对瞬时性干扰:系统应在干扰消失后恢复到初始的稳态运行方式: 对永久性干扰:系统应在经历短时的暂态过程后达到邻近初始运 行状态的一个新的稳态运行方式

电力系统静态稳定研究的目的: 不是确定在小干扰下系统的准确的响应过程, 而是确定系统运行参数变化的性质和趋势, 以便从中判断系统的稳定状况, 是对能力的研究,而不是对过程的研究

静态稳定的特点: 起因:系统受到小的干扰,例如负荷的随机涨落、汽轮机蒸汽压力的波动、 发电机端电压发生小的偏移,等等。 过程:系统将会偏离平衡点。 结果:如果这种偏离很小,干扰消失后,系统又重新恢复平衡, 则系统是静态稳定的。 特点:系统的状态变量偏离很小,从而允许把描述系统的状态方程线性化
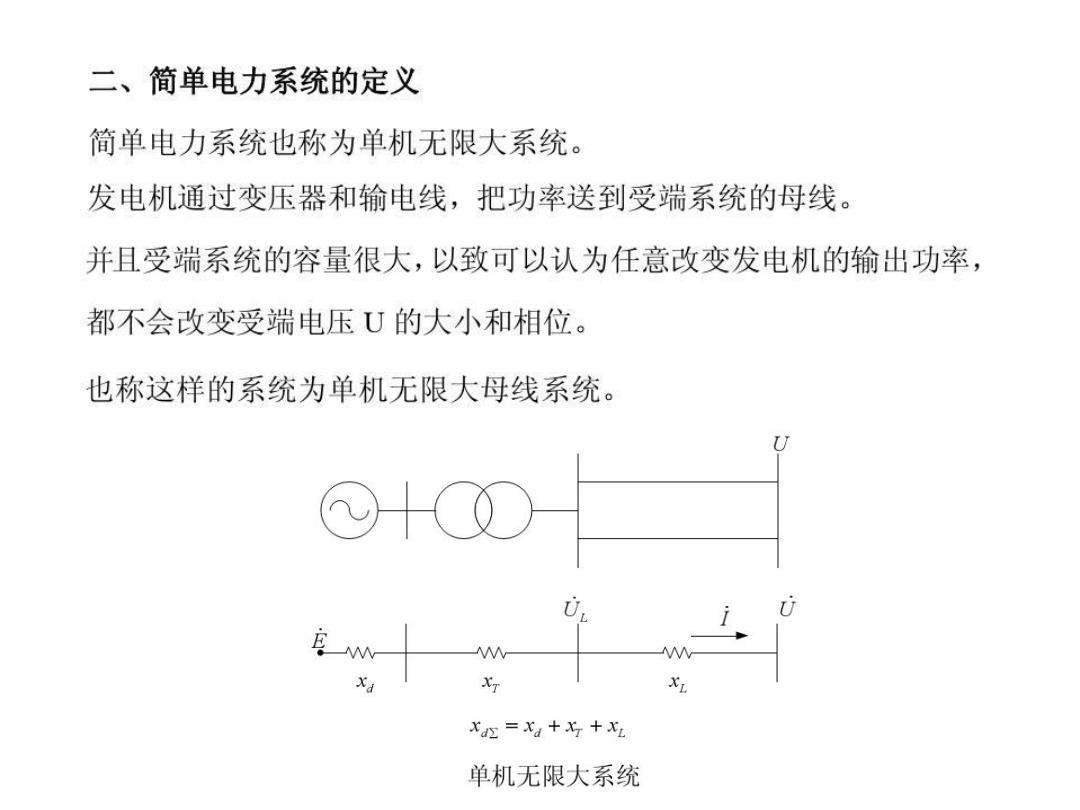
二、简单电力系统的定义 简单电力系统也称为单机无限大系统。 发电机通过变压器和输电线,把功率送到受端系统的母线。 并且受端系统的容量很大,以致可以认为任意改变发电机的输出功率, 都不会改变受端电压U的大小和相位。 也称这样的系统为单机无限大母线系统。 U ⊙ xdx =xd+x+x 单机无限大系统

“无限大容量母线”: 母线上接有无限大容量电源”,即z=0、U=定值, 使得与之相联的母线电压大小恒定外, 还体现在惯性时间常数为无限大,则转子的转速恒为同步 转速,E或U的交变频率恒等于同步频率。 U ⊙d xax =xd+x+x 单机无限大系统

三、单机无限大系统理想情况分析 理想情况: E 发电机为隐极机→发电机输出的电磁功率为P。= sinδ; xa 2 不考虑发电机励磁调节器的作用→认为发电机的空载电势E恒定: (不考虑动磁调节器的作用→发电机的空载电势E。恒定: 考虑动磁调节器作用→发电机的暂态电势E,恒定: 加装电在稳定器→发电机的机端电在U。恒定) 不计原动机调速器作用→原动机的机械功率P,不变: ④ 忽略发电机的风阻、摩擦等机械阻力和各阻尼的影响→P。=0。 xE=/+为+x 单机无限大系统
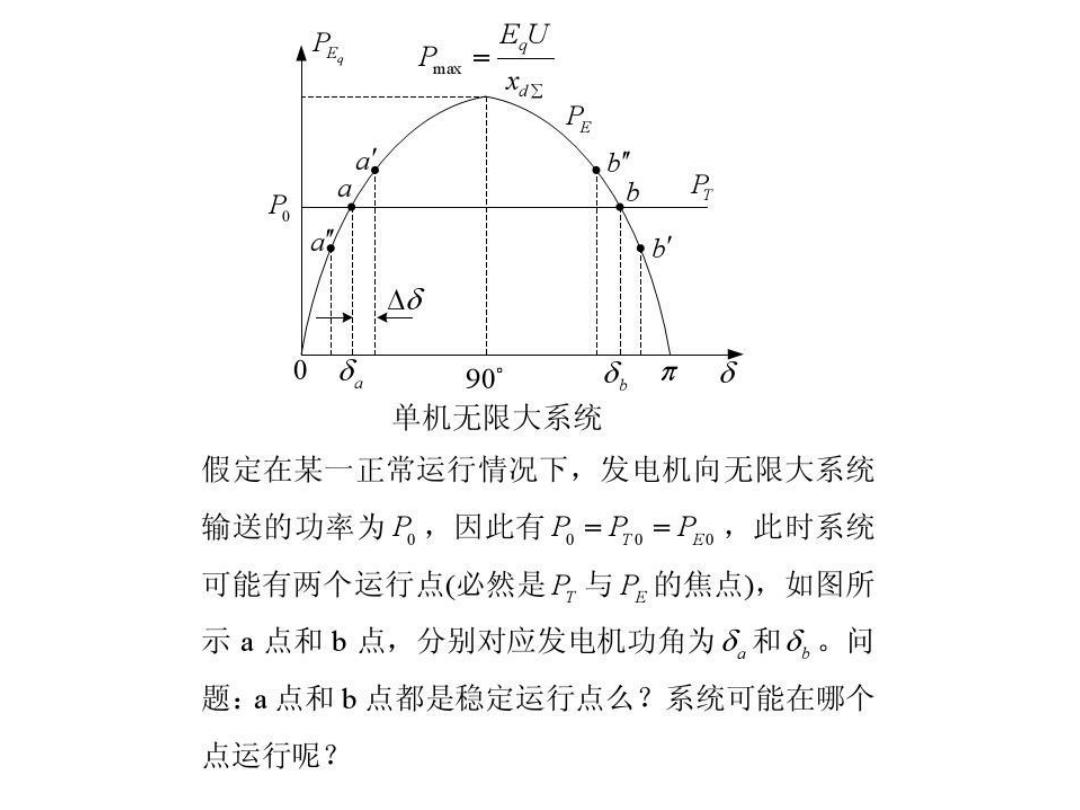
P EU max xa b" a b P B' A 90° π 单机无限大系统 假定在某一正常运行情况下,发电机向无限大系统 输送的功率为P,因此有P=P。=Po,此时系统 可能有两个运行点(必然是P,与P的焦点),如图所 示a点和b点,分别对应发电机功角为6和6,。问 题:a点和b点都是稳定运行点么?系统可能在哪个 点运行呢?
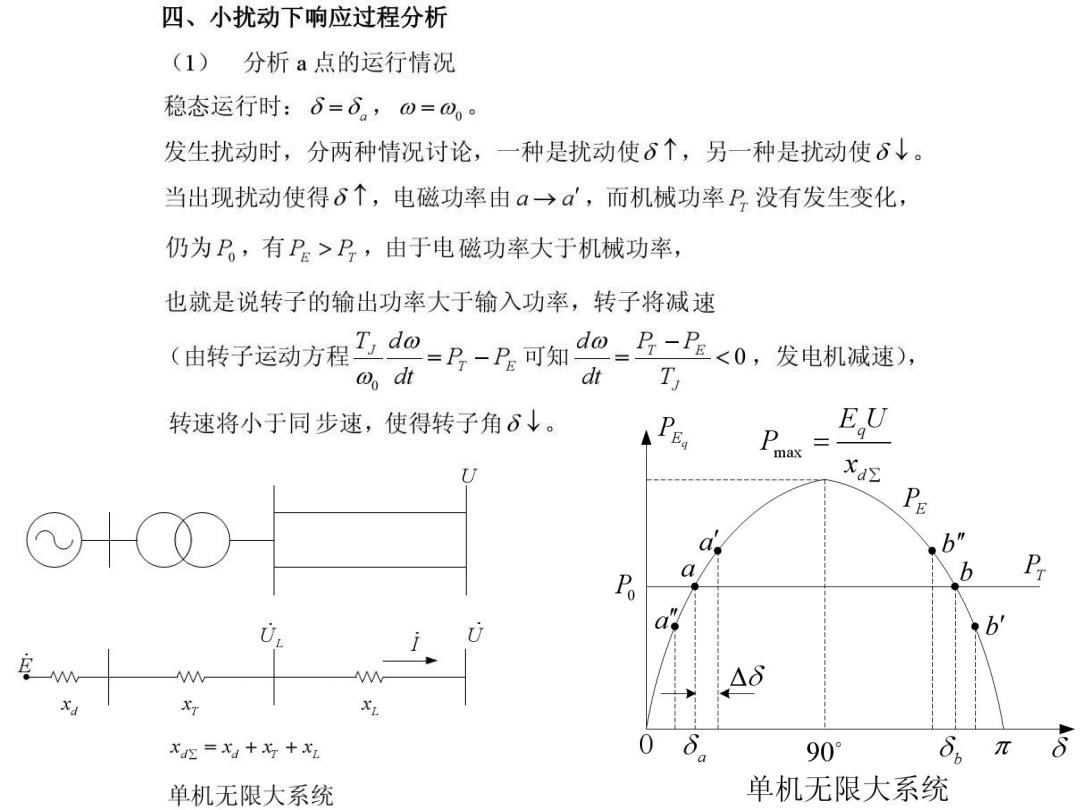
四、小扰动下响应过程分析 (1)分析a点的运行情况 稳态运行时:6=δ,0=0 发生扰动时,分两种情况讨论,一种是扰动使6个,另一种是扰动使δ↓。 当出现扰动使得δ个,电磁功率由a→a,而机械功率P,没有发生变化, 仍为P,有P。>P,由于电磁功率大于机械功率, 也就是说转子的输出功率大于输入功率,转子将减速 (由转子运动方程d扣=乃-R可知p_B二品<0,发电机被速)。 w dt d T 转速将小于同步速,使得转子角δ↓。 P EU max xa P Po b Ao xdx=xd+xT+xL π a 90° 单机无限大系统 单机无限大系统