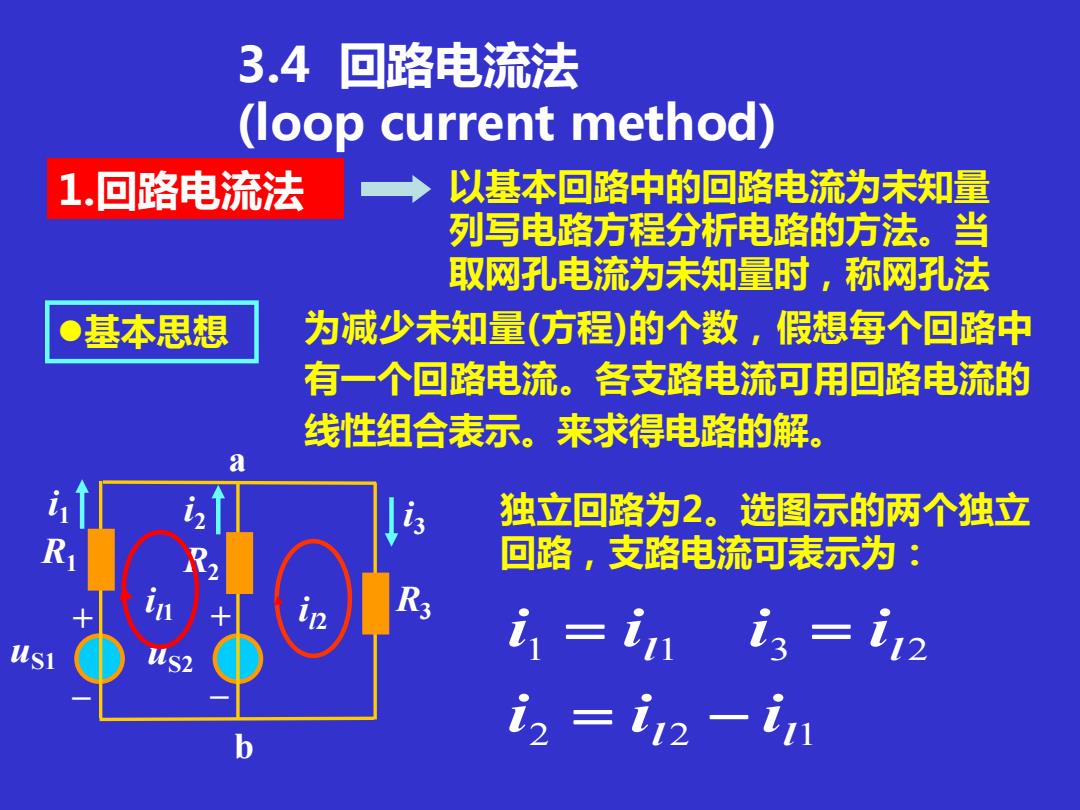
3.4 回路电流法 (loop current method) 1.回路电流法 以基本回路中的回路电流为未知量 列写电路方程分析电路的方法。当 取网孔电流为未知量时,称网孔法 基本思想 为减少未知量(方程)的个数,假想每个回路中 有一个回路电流。各支路电流可用回路电流的 线性组合表示。来求得电路的解。 独立回路为2。选图示的两个独立 回路,支路电流可表示为: i1=i1 i3=i2 i2=i12-1
3.4 回路电流法 (loop current method) ⚫基本思想 为减少未知量(方程)的个数,假想每个回路中 有一个回路电流。各支路电流可用回路电流的 线性组合表示。来求得电路的解。 1.回路电流法 以基本回路中的回路电流为未知量 列写电路方程分析电路的方法。当 取网孔电流为未知量时,称网孔法 i1 i3 uS1 uS2 R1 R2 R3 b a + – + – i2 i l1 i l2 独立回路为2。选图示的两个独立 回路,支路电流可表示为: 2 2 1 1 1 3 2 l l l l i i i i i i i = − = =
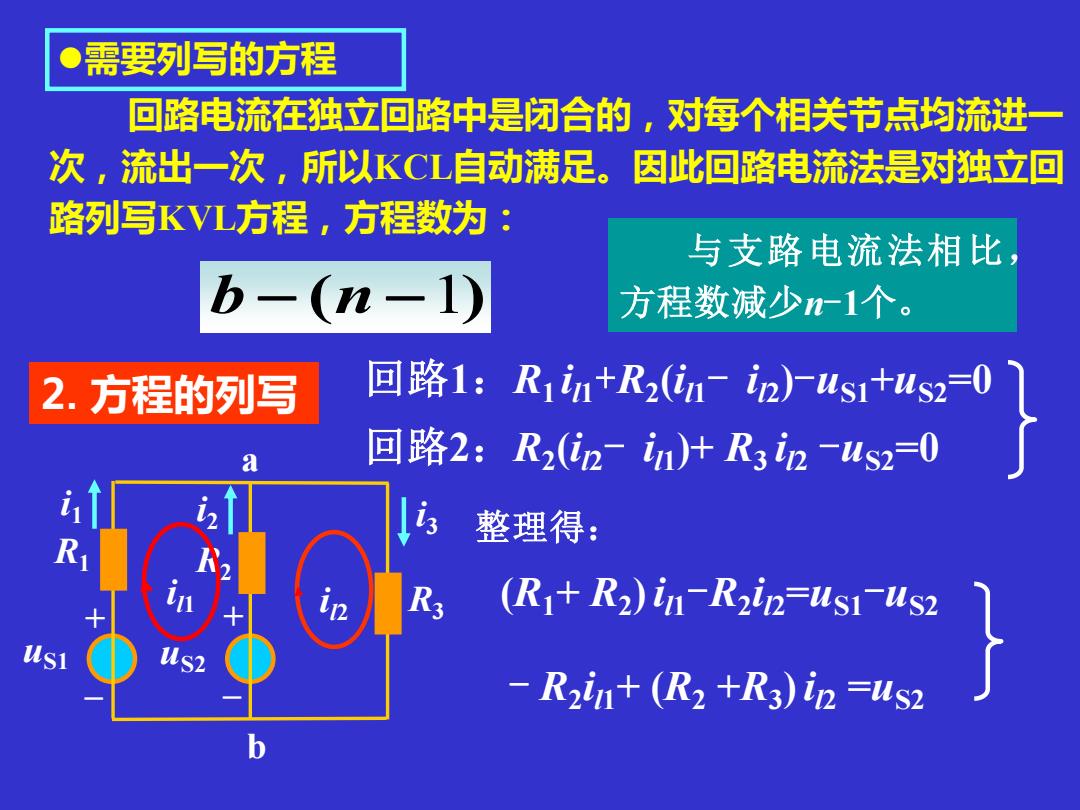
需要列写的方程 回路电流在独立回路中是闭合的,对每个相关节点均流进一 次,流出一次,所以KCL自动满足。因此回路电流法是对独立回 路列写KVL方程,方程数为 与支路电流法相比 b- n-1 方程数减少-1个。 2.方程的列写 ▣路1:R1n+Rz(inn)-us1tus20 a ▣路2:Rz(i2ntR3n-us2=0 整理得: (R+R2)in-R2in=us1-us2 S1 S2 -R2in+(R2 +R3)in =us2
回路电流在独立回路中是闭合的,对每个相关节点均流进一 次,流出一次,所以KCL自动满足。因此回路电流法是对独立回 路列写KVL方程,方程数为: ⚫需要列写的方程 与支路电流法相比, 方程数减少n-1个。 回路1:R1 i l1+R2 (i l1- i l2 )-uS1+uS2=0 回路2:R2 (i l2- i l1 )+ R3 i l2 -uS2=0 整理得: (R1+ R2 )i l1-R2 i l2=uS1-uS2 - R2 i l1+ (R2 +R3 )i l2 =uS2 b − (n −1) i1 i3 uS1 uS2 R1 R2 R3 b a + – + – i2 i l1 i l2 2. 方程的列写

观察可以看出如下规律: R11R1+R2 回路1的自电阻。等于回路1中所有电阻之和。 R22R2+R3 回路2的自电阻。等于回路2中所有电阻之和。 自电阻总为正。 R12=R21=-R2 回路1、回路2之间的互电阻。 当两个回路电流流过相关支路方向相同时,互电阻取 正号;否则为负号。 un=usi-us2 回路1中所有电压源电压的代数和。 up=us2 回路2中所有电压源电压的代数和。 当电压源电压方向与该回路方向一致时,取负号;反之 取正号
R11=R1+R2 回路1的自电阻。等于回路1中所有电阻之和。 观察可以看出如下规律: R22=R2+R3 回路2的自电阻。等于回路2中所有电阻之和。 自电阻总为正。 R12= R21= –R2 回路1、回路2之间的互电阻。 当两个回路电流流过相关支路方向相同时,互电阻取 正号;否则为负号。 ul1= uS1-uS2 回路1中所有电压源电压的代数和。 ul2= uS2 回路2中所有电压源电压的代数和。 当电压源电压方向与该回路方向一致时,取负号;反之 取正号

由此得标准形式的方程: Ruin+R12in=usn R12in+R2ip=usm 对于具有=b-(-1)个回路的电路,有 Ruin+Rip+...+Ruiuusn R2in+R2in+...+Rzinusp Rnin+Rpin+...+Ruiu-usu 其中: R:自电阻(为正) +:流过互阻的两个回路电流方向相同 R:互电阻 流过互阻的两个回路电流方向相反 0:无关
R11i l1+R12i l2 =uSl1 R12i l1+R22i l2 =uSl2 由此得标准形式的方程: 对于具有 l=b-(n-1) 个回路的电路,有: 其中: Rjk:互电阻 + : 流过互阻的两个回路电流方向相同 - : 流过互阻的两个回路电流方向相反 0 : 无关 R11i l1+R12i l2+ …+R1l i ll=uSl1 … R21i l1+R22i l2+ …+R2l i ll=uSl2 Rl1 i l1+Rl2 i l2+ …+Rll i ll=uSll Rkk:自电阻(为正)
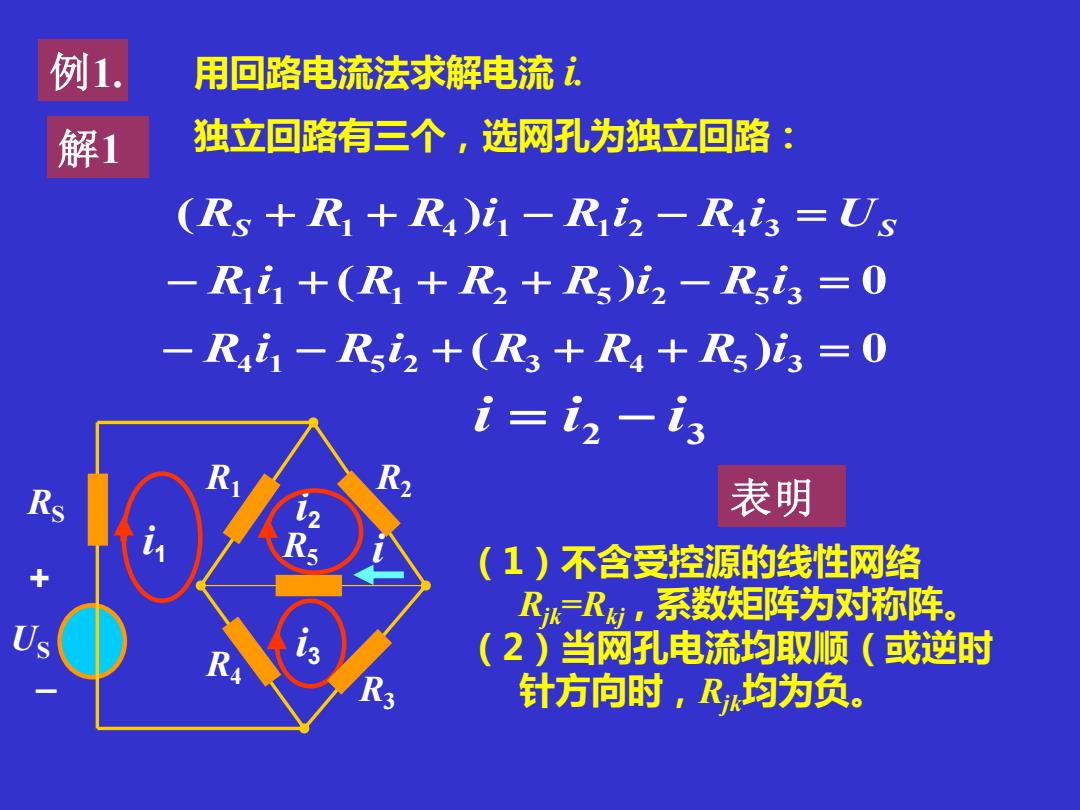
例1. 用回路电流法求解电流, 解1 独立回路有三个,选网孔为独立回路: (Rs +R+R)i-Riz-Rais =Us -R1+(R1+R2+Rs)i2-R3=0 -R1-Ri2+(R3+R4+R)i3=0 i=i,-is Rs 表明 (1)不含受控源的线性网络 R一R,系数矩阵为对称阵。 ● (2)当网孔电流均取顺(或逆时 针方向时,R均为负
例1. 用回路电流法求解电流 i. 解1 独立回路有三个,选网孔为独立回路: i1 i3 i2 S US (R + R1 + R4 )i 1 − R1 i 2 − R4 i 3 = − R1 i 1 + (R1 + R2 + R5 )i 2 − R5 i 3 = 0 − R4 i 1 − R5 i 2 + (R3 + R4 + R5 )i 3 = 0 (1)不含受控源的线性网络 Rjk=Rkj , 系数矩阵为对称阵。 (2)当网孔电流均取顺(或逆时 针方向时,Rjk均为负。 表明 2 3 i = i − i RS R5 R4 R3 R1 R2 US + _ i
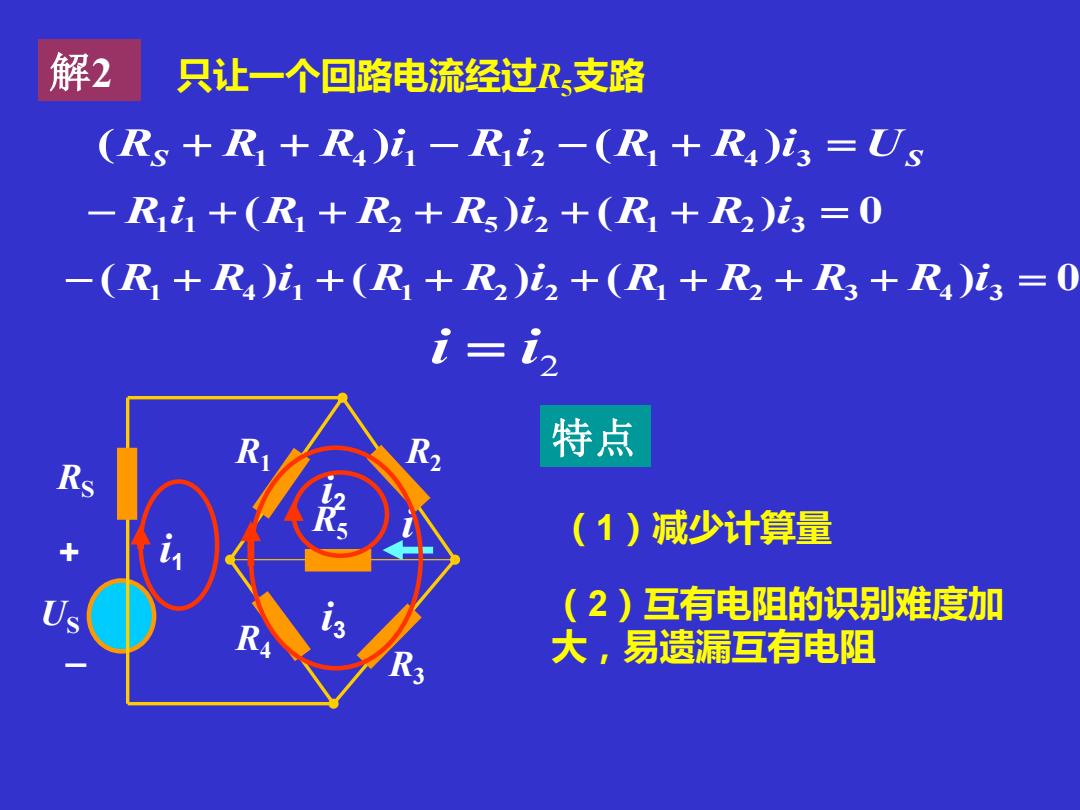
解2 只让一个回路电流经过R支路 (Rs +R+R)i-Rii-(R+R)i3=Us -R1+(R+R2+Rs)i2+(R1+R2)i3=0 -(R1+R4)i1+(R+R)i2+(R1+R2+R3+R4)i3=0 i=in 特点 Rs (1)减少计算量 (2)互有电阻的识别难度加 大,易遗漏互有电阻
RS R5 R4 R3 R1 R2 US + _ i 解2 只让一个回路电流经过R5支路 S US (R + R1 + R4 )i 1 − R1 i 2 − (R1 + R4 )i 3 = − R1 i 1 + (R1 + R2 + R5 )i 2 + (R1 + R2 )i 3 = 0 − (R1 + R4 )i 1 + (R1 + R2 )i 2 + (R1 + R2 + R3 + R4 )i 3 = 0 i1 i3 i2 2 i = i 特点 (1)减少计算量 (2)互有电阻的识别难度加 大,易遗漏互有电阻

回路法的一般步骤: (1)选定=b-(-1)个独立回路,并确定其绕行方向; (2)对1个独立回路,以回路电流为未知量,列写其KVL方程; (3)求解上述方程,得到1个回路电流: (4)求各支路电流(用回路电流表示); (5)其它分析
回路法的一般步骤: (1) 选定l=b-(n-1)个独立回路,并确定其绕行方向; (2) 对l 个独立回路,以回路电流为未知量,列写其KVL方程; (3) 求解上述方程,得到l 个回路电流; (5) 其它分析。 (4) 求各支路电流(用回路电流表示);
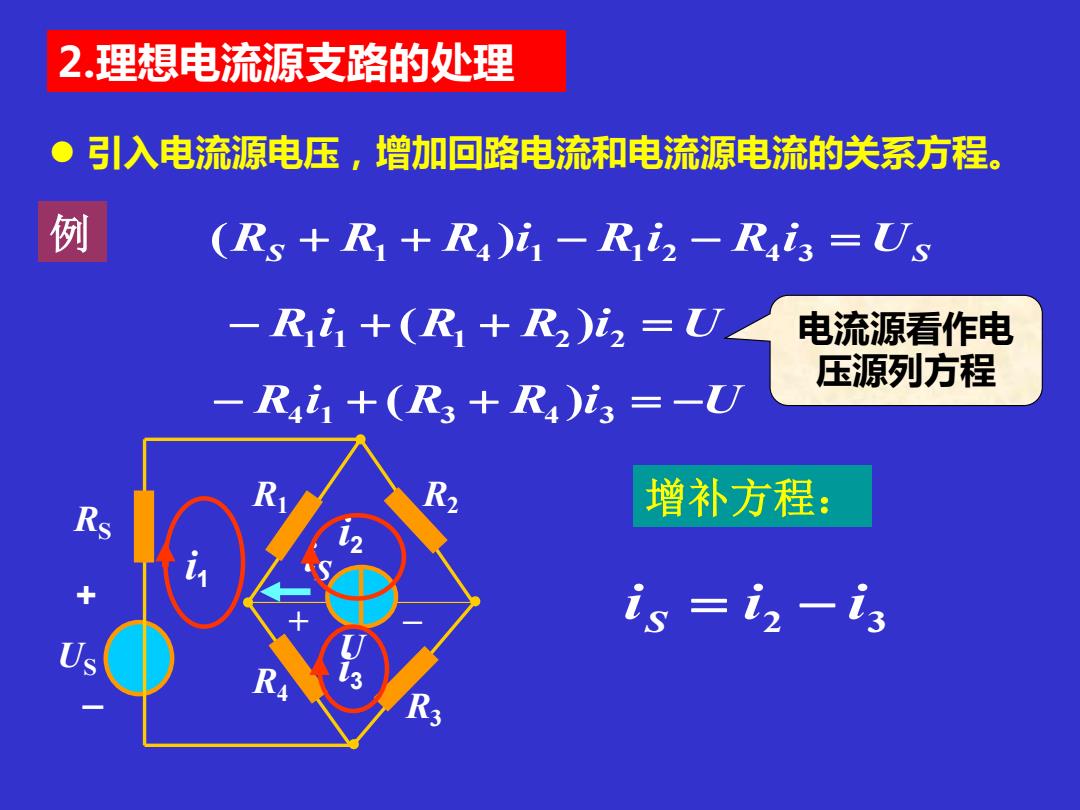
2.理想电流源支路的处理 引入电流源电压,增加回路电流和电流源电流的关系方程。 例 (Rs +Ri+R)i1-Riiz-Ris =Us -Ri1+(R1+R2)i2=U 电流源看作电 压源列方程 -R4i1+(R3+R4)i3=-U Rs 增补方程: is iz -is
2.理想电流源支路的处理 ⚫ 引入电流源电压,增加回路电流和电流源电流的关系方程。 例 RS R4 R3 R1 R2 US + _ iS U _ + i1 i3 i2 S US (R + R1 + R4 )i 1 − R1 i 2 − R4 i 3 = − R1 i 1 + (R1 + R2 )i 2 = U − R4 i 1 + (R3 + R4 )i 3 = −U 2 3 i i i S = − 电流源看作电 压源列方程 增补方程:

● 选取独立回路,使理想电流源支路仅仅属于一个回路, 该回路电流即上。 例 (Rs+R1+R4)i1-i2-(R1+R4)i3=Us i,is 为已知电流,实际减少了一方程 -(R+R)i1+(R1+R2)i2+(R1+R2+R3+R4)i3=0 Rs
⚫ 选取独立回路,使理想电流源支路仅仅属于一个回路, 该回路电流即 IS 。 RS R4 R3 R1 R2 US + _ iS i1 i3 i2 S US 例 (R + R1 + R4 )i 1 − R1 i 2 − (R1 + R4 )i 3 = − (R1 + R4 )i 1 + (R1 + R2 )i 2 + (R1 + R2 + R3 + R4 )i 3 = 0 S i = i 2 为已知电流,实际减少了一方程
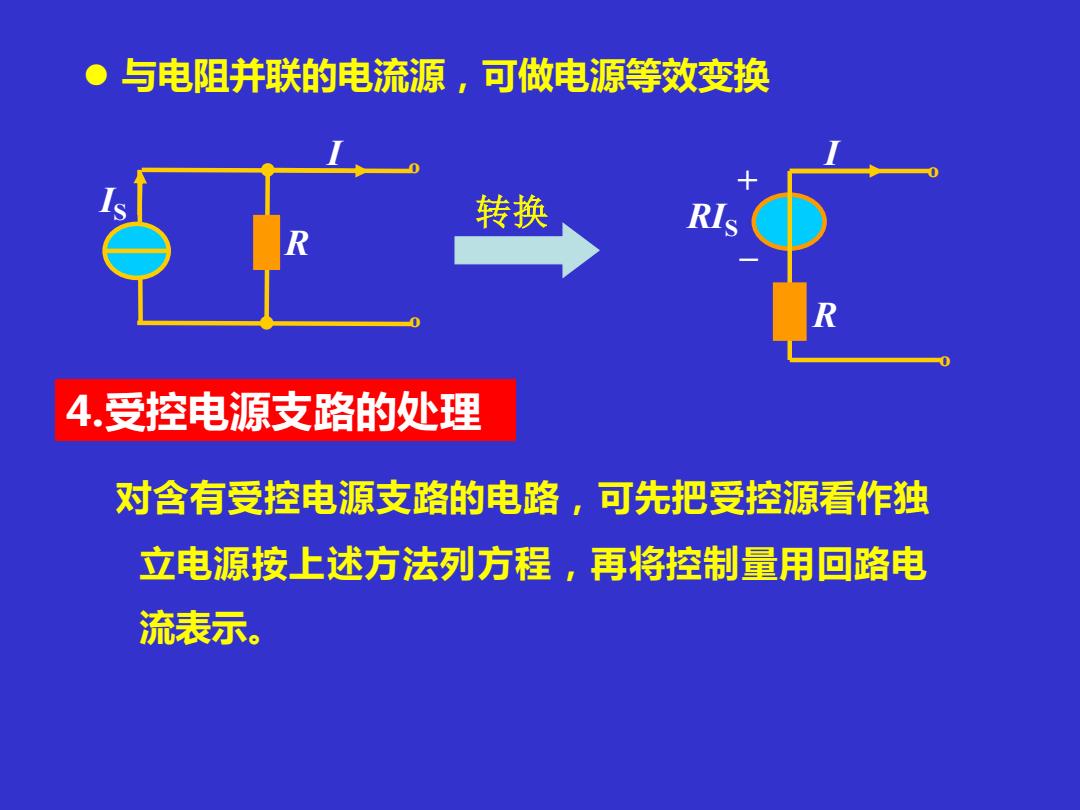
●与电阻并联的电流源,可做电源等效变换 转换 4.受控电源支路的处理 对含有受控电源支路的电路,可先把受控源看作独 立电源按上述方法列方程,再将控制量用回路电 流表示
⚫ 与电阻并联的电流源,可做电源等效变换 I R IS º º 转换 + _ RIS I R º º 4.受控电源支路的处理 对含有受控电源支路的电路,可先把受控源看作独 立电源按上述方法列方程,再将控制量用回路电 流表示