例2 t0时,开关K打开,求t>0后的i、W及电流源的端 电压。 5① 102 解 这是一个RL电路零状态响 应问题,先化简电路,有: 102 2H5 =10+10=202 Us=2×10=20/ t=L/Rg=2/20=0.1s 仑0 iL(o)=Us/Reo =1A iz(t)=(1-e10r)A 2H3 ul (t)Use-1 20e-iy z W=51s+10iz+uz=20+10e-1rV
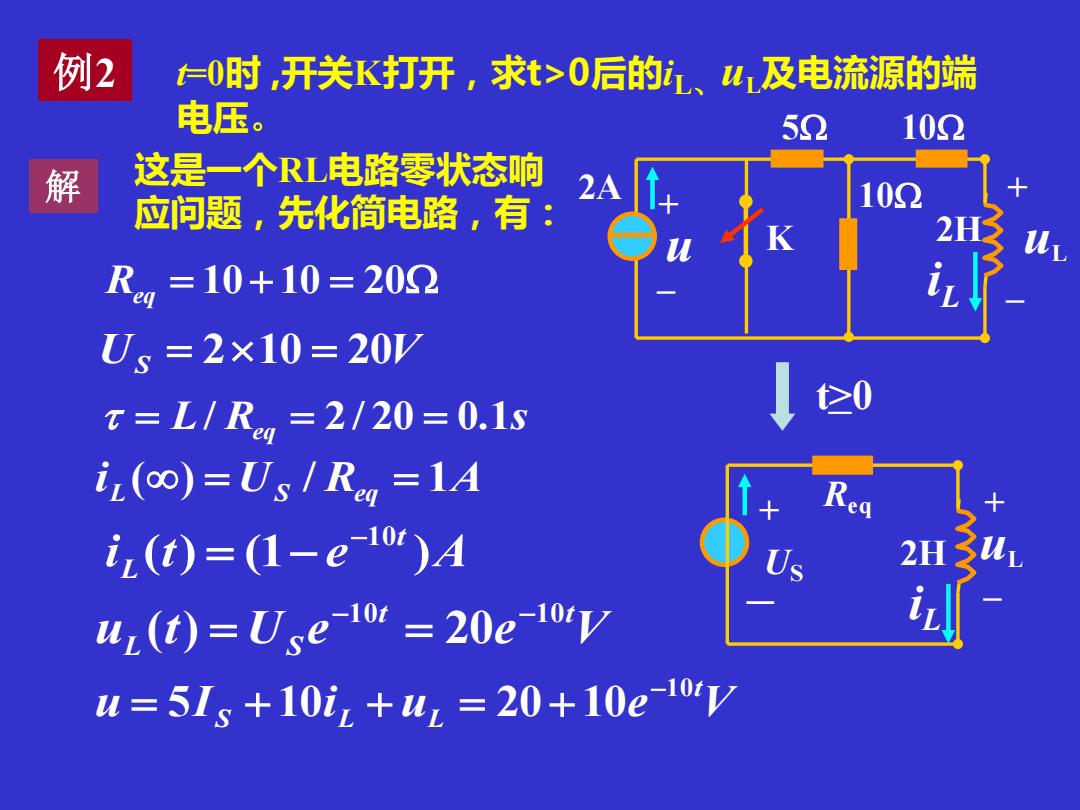
例2 t=0时 ,开关K打开,求t>0后的iL、 uL及电流源的端 电压。 解 这是一个RL电路零状态响 应问题,先化简电路,有: iL K + – uL 2H 10 2A 10 5 + – u t>0 iL + – U 2H uL S + Req - Req = 10 + 10 = 20 US = 210 = 20V L R s = / eq = 2 / 20 = 0.1 i t e A t L ( ) (1 ) −10 = − u t U e e V t t L S 10 10 ( ) 20 − − = = i L () = US / Req = 1A u I i u e V t S L L 1 0 5 10 20 10 − = + + = +
6.4一阶电路的全响应 全响应 电路的初始状态不为零,同时又有外加 激励源作用时电路中产生的响应。 1.全响应 (=0) 以RC电路为例,电路微分方程: RC duc+uc =Us dt 由起始值定A 解答为 uc(t)=uc+uc uc(0-)=Uo 稳态解uc'=Us uc(0)=U0=A+Us 暂态解化=Ae :A=U0-Us TRC
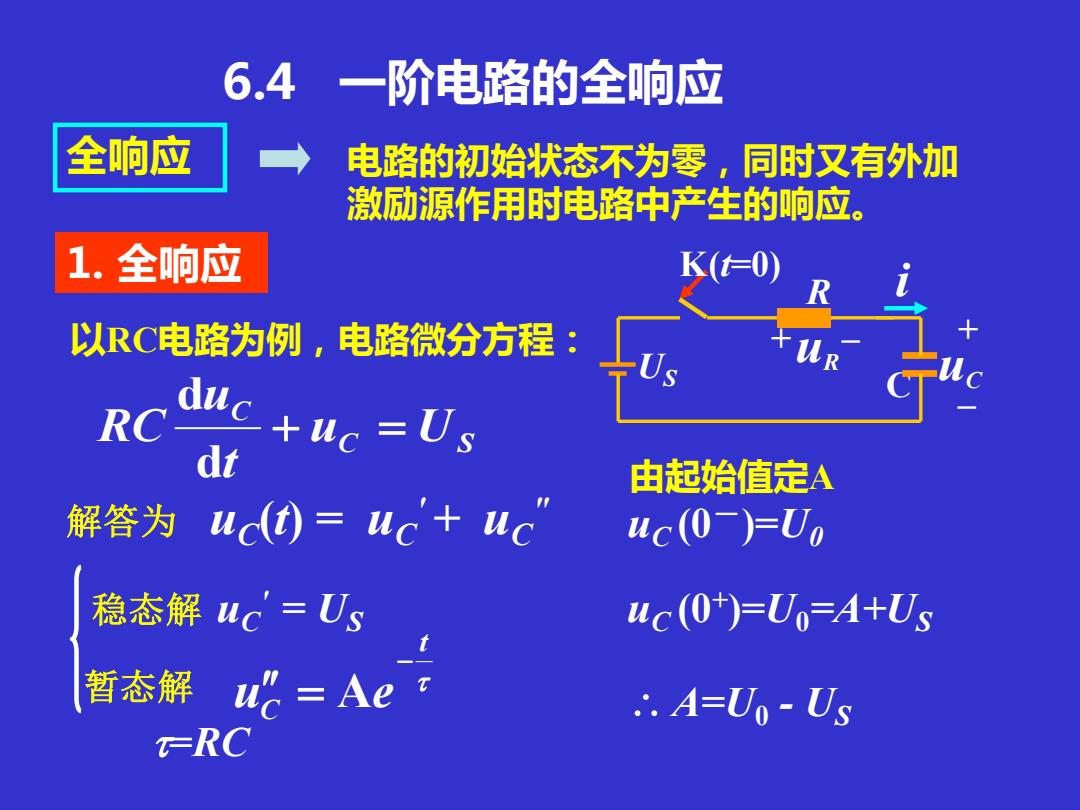
6.4 一阶电路的全响应 电路的初始状态不为零,同时又有外加 激励源作用时电路中产生的响应。 i K(t=0) US +u – R C + – uC R C S C u U t u RC + = d d 解答为 uC (t) = uC ' + uC " uC (0-)=U0 以RC电路为例,电路微分方程: =RC 1. 全响应 全响应 稳态解 uC ' = US 暂态解 t C u e − = A uC (0+ )=U0=A+US A=U0 - US 由起始值定A
-t uc =Us+Ae'=Uls+(Uo-Us)e t≥0 强制分量(稳态解) 自由分量(暂态解 2.全响应的两种分解方式 (1)着眼于电路的两种工作状态 稳态解 Us 全响应三 全解 强制分量(稳态解 0 自由分量(暂态解 U 暂态解 物理概念清晰
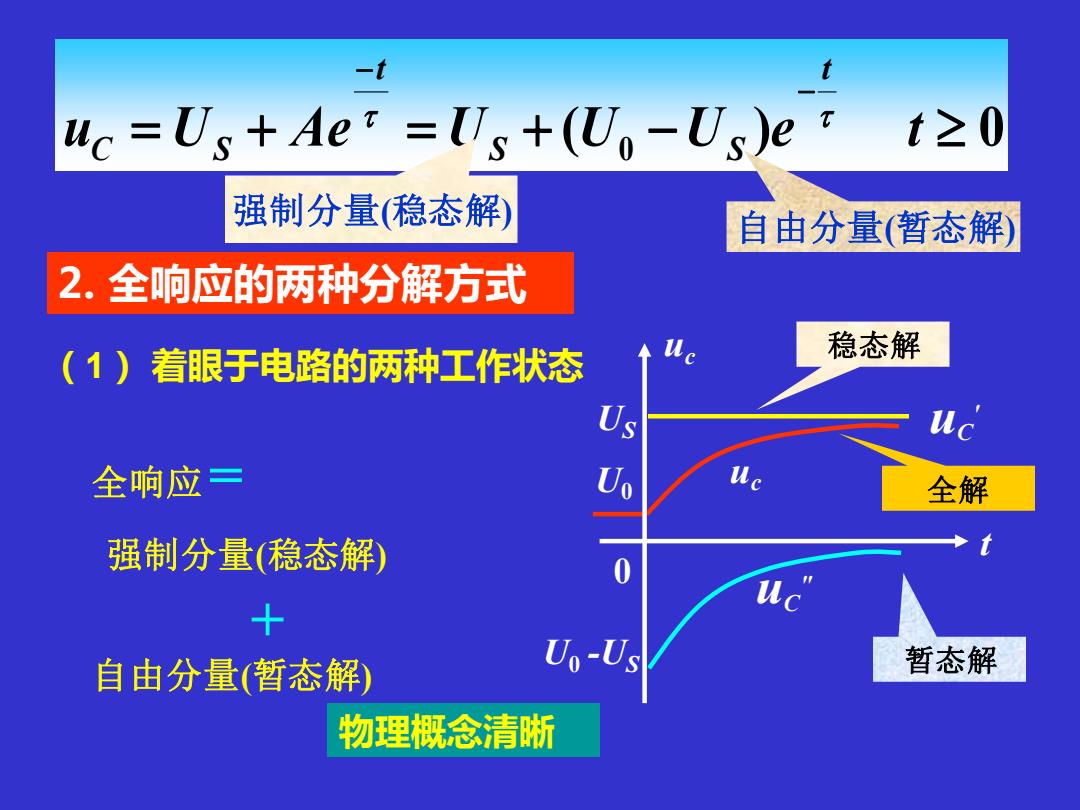
2. 全响应的两种分解方式 ( ) 0 = + = + 0 − − − u U Ae U U U e t t S S t C S 强制分量(稳态解) 自由分量(暂态解) uC " U0 -US 暂态解 uC U ' S 稳态解 U0 uc 全解 t uc 0 全响应 = 强制分量(稳态解) + 自由分量(暂态解) (1) 着眼于电路的两种工作状态 物理概念清晰

(2).着眼于因果关系 便于叠加计算 -f uc=Us+Ae:=Us+(Uo-Us)e t≥0 uc =Us(1-e )+Ue (t≥0) 零状态响应 零输入响应 全响应=零状态响应十零输入响应 K0) uc(O)=Uo uc(0-)=0 uc(O)=Uo
i K(t=0) US +u – R C + – uC R uC (0-)=U0 i K(t=0) US +u – R C + – uC R = uC (0-)=0 + uC (0-)=U0 C + – uC i K(t=0) +u – R R 全响应= 零状态响应 + 零输入响应 零状态响应 零输入响应 (1 ) ( 0) = − + 0 − − u U e U e t t t C S (2). 着眼于因果关系 便于叠加计算 ( ) 0 = + = + 0 − − − u U Ae U U U e t t S S t C S

uc =Us(I-e :)+Ue (t≥0) 零状态响应 零输入响应 全响应 零状态响应 0 零输入响应
(1 ) ( 0) = − + 0 − − u U e U e t t t C S 零状态响应 零输入响应 t uc 0 US 零状态响应 全响应 零输入响应 U0

例1 t0时,开关K打开,求t>0后的i吃、4 解 这是一个RL电路全响应问 82 42 题,有: iz(0)=iz(0)=Us/R1=6A K(=0 0.6H x=L/R=0.6/12=1/20s 零输入响应:(t)=6e20A 零状态响应:2() 2 12 1-e-20r)A 全响应:i2()=6e20+2(1-e20r)=2+4e20A
例1 t=0时 ,开关K打开,求t>0后的iL、 uL 解 这是一个RL电路全响应问 题,有: = L/ R = 0.6/12 = 1/ 20s i L (0 ) = i L (0 ) = US / R1 = 6A − + i t e A t L 20 ( ) 6 − 零输入响应: = i t e A t L (1 ) 12 24 ( ) −20 = − 零状态响应: i t e e e A t t t L 20 20 20 ( ) 6 2(1 ) 2 4 − − − = + − = + 全响应: iL K(t=0) + – 24V 0.6H 4 + - uL 8

或求出稳态分量:i,(∞)=24/12=2A 全响应: i (t)=2+Ae 2A 代入初值有: 6=2+A A=4 例2 t广0时,开关K闭合,求t>O后的iC、4c及电流源两端 的电压。(uc(0)=1,C=1F) 解 这是一个RC电路全响应 问题,有: 1Ω 稳态分量:wc(∞)=10+1=11V T=RC=(1+1)×1=2s 全响应:4c(t)=11+Ae0.5V→A=-10
或求出稳态分量: i L () = 24/12 = 2A 全响应: i t Ae A t L 20 ( ) 2 − = + 代入初值有: 6=2+A A=4 例2 t=0时 ,开关K闭合,求t>0后的iC、 uC及电流源两端 的电压。 解 这是一个RC电路全响应 问题,有: + – 10V 1A 1 + - uC 1 + - u 1 稳态分量: uC () = 10+1 = 11V (u (0 ) 1V,C 1F) C = = − 全响应: u t Ae V t C 0.5 ( ) 11 − = + = RC = (1+1)1 = 2s A=-10
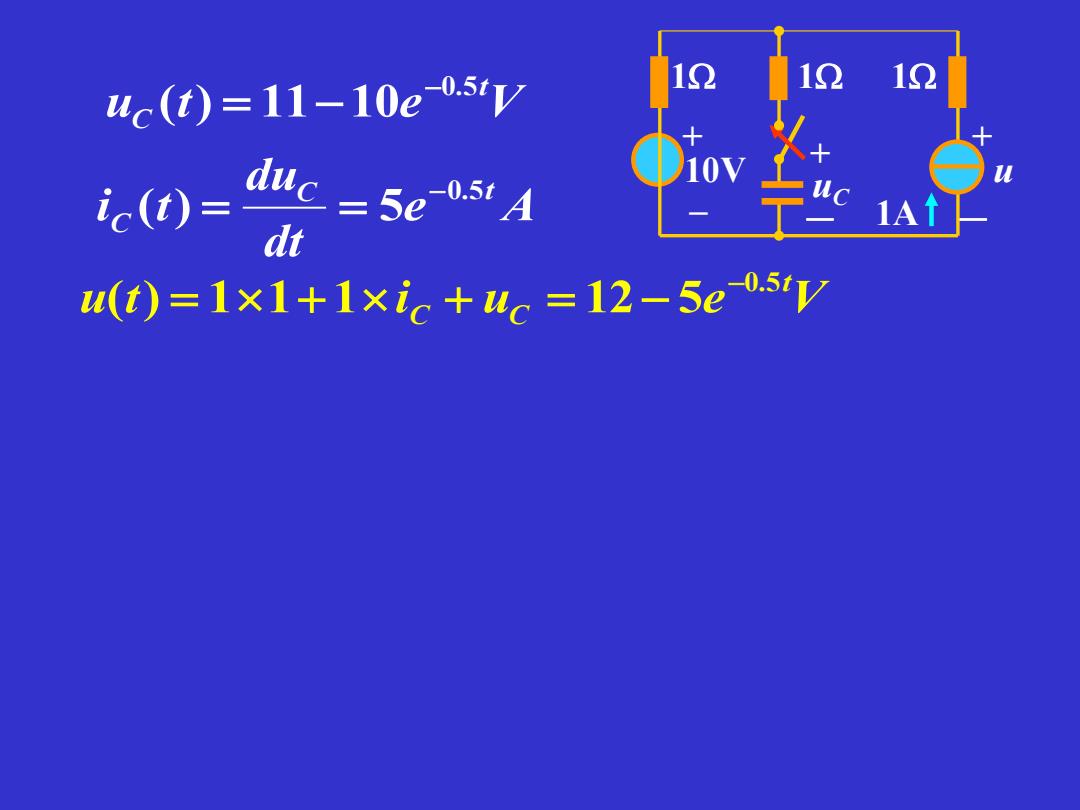
uc(t)=11-10e.sy 12 1Ω 1Ω 0-路=54 uc (t)=1×1+1×ic+4c=12-5e.sy
u t e V t C 0 . 5 ( ) 11 10 − = − e A dt du i t C t C 0 . 5 ( ) 5 − = = +– 10V 1A1 +-u C 1 +- u 1 u t i u e V t C C 0.5 ( ) 1 1 1 12 5 − = + + = −

3.三要素法分析一阶电路 af +bf=c 阶电路的数学模型是一阶微分方程: dt 其解答一般形式为: f(t)=f(co)+Ae 令t=0*f(0)=f(o)+A→ A=f(0*)-f(o) f(t)=f(oo)+[f(0)-f(o)]e f) 稳态解→用t→∞的稳态电路求解 三要素 f(0*) 初始值一→用0等效电路求解 时间常数求等效电阻 分析一阶电路问题转为求解电路的三个要素的问题
3. 三要素法分析一阶电路 t f t f f f e − + ( ) = () +[ (0 ) − ()] + 时间常数 初始值 稳态解 三要素 (0 ) ( ) f f 一阶电路的数学模型是一阶微分方程: t f t f e − ( ) = () + A 令 t = 0+ (0 ) = () + A + f f = (0 ) − () + A f f bf c dt d f a + = 其解答一般形式为: 分析一阶电路问题转为求解电路的三个要素的问题 用0 +等效电路求解 用t→的稳态电路求解 求等效电阻
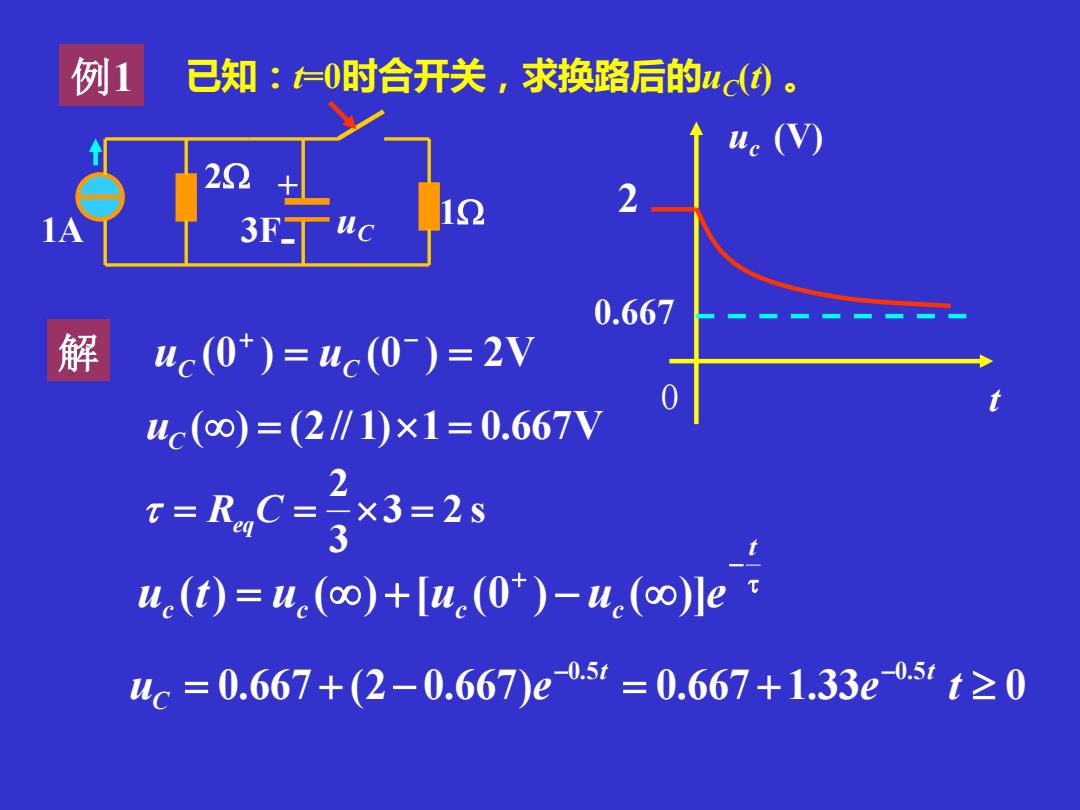
例1 已知:t0时合开关,求换路后的4(t)。 ue (V) 22 3F 0.667 解 uc(0*)=uc(0)=2V uc(o)=(21∥1)×1=0.667V T=RC-2x3-2s 2 3 ue(t)=uc(00)+lu.(O*)-u(o)le uc=0.667+(2-0.667)e0.5=0.667+1.33e.5t≥0
(0 ) = (0 ) = 2V + − uC uC uC () = (2// 1)1 = 0.667V 3 2 s 3 2 = ReqC = = 0.667 (2 0.667) 0.667 1.33 0 0.5 0.5 = + − = + − − u e e t t t C 1A 2 例1 1 3F + - uC 已知:t=0时合开关,求换路后的uC (t) 。 解 t uc 2 (V) 0.667 0 − + = + − t c c c c u (t) u ( ) [u (0 ) u ( )]e