
第9章正弦稳态电路的分析 重点: 1.阻抗和导纳; 2.正弦稳态电路的分析; 3.正弦稳态电路的功率分析;

9.1阻抗和导纳 1.阻抗 正弦稳态情况下 无源 线性 U 定义阻抗Z==Z|∠p: 欧姆定律的 相量形式 U 阻抗模 单位:2 阻抗角

当无源网络内为单个元件时有: + R -· =R =X。 Q +-。 3 =j@L=jX Z可以是实数,也可以是虚数

2.RLC串联电路的阻抗 R joL ++r-+4L ++R+0 1 Uc joC a 由KVL: -tat-Ritimi-ci =[R+j(@L-)]i=[R+j(X:-Xc)]i =(R+jX)i 2、 U R+L-jaC=R+x=Zc贝

Z一复阻抗;R一电阻(阻抗的实部:X一电抗(阻抗的虚部: ☑一复阻抗的模;9,一阻抗角。 |Z=√R2+X 转换关系: X o,arctg R 或 R=Zcosp: X=Zsing. 9,=Ψ,-Ψ 阻抗三角形 ☑
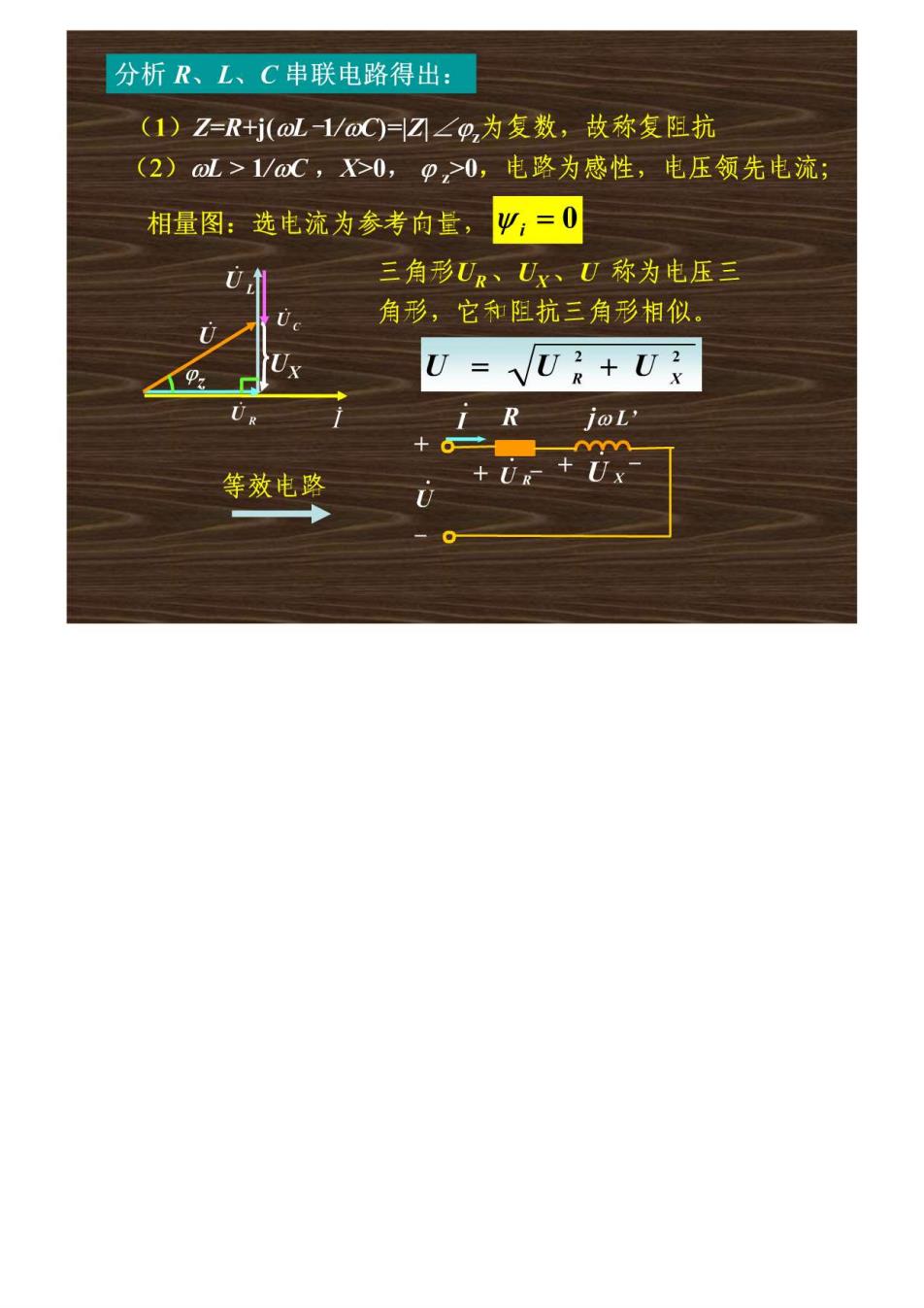
分析R、L、C串联电路得出: (1)Z=R+j(oL-1/oC☑∠p,为复数,故称复阻抗 (2)L>1/@oC,X0,p,>0,电路为感性,电压领先电流; 相量图:选电流为参考向董,少=0 三角形U、U、U称为电压三 角形,它和阻抗三角形相似。 U=V0R+U joL' 等效电路 +0R+0x
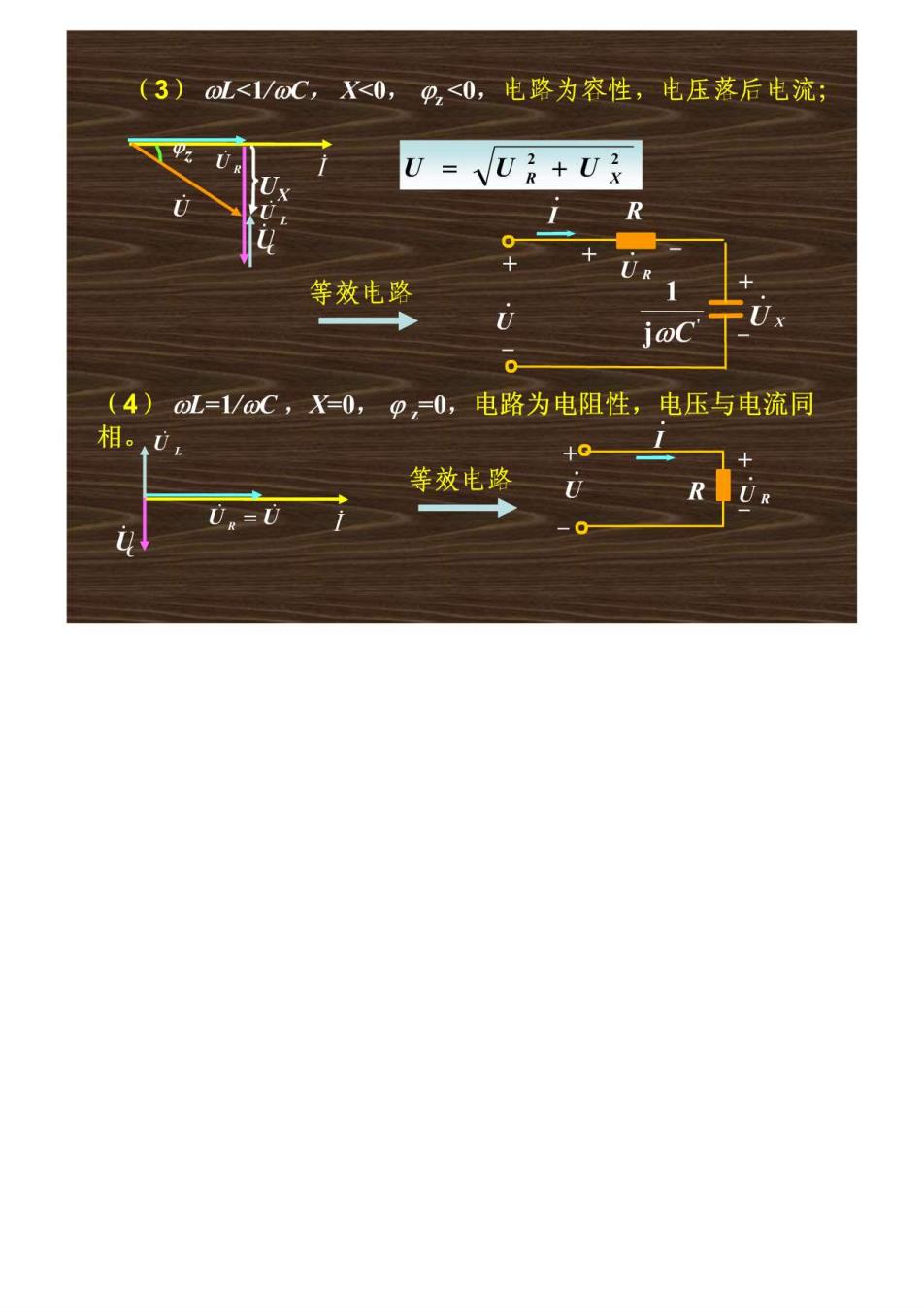
(3)oL<1/@oC,X<0,②,<0,电路为容性,电压落后电流; U=Ui+Ux R 等效电路 U j@C (4)oL=1/oC,X=0,p,=0,电路为电阻性,电压与电流同 相。0 +0 等效电路 U R Ur=U

例 已知:R=152,L=0.3mH,C=0.2uF, ++R +元 u=5√2cos(ot+60) e. 4cf=3×10Hz. 求i,uR,u,c 解 R joL 其相量模型为: ++UR +UL U=5∠60°V U c jωC joL=j2π×3×104×0.3×103=j56.52 1 Z=R+jol-j0C=15+565-265=354/63.40

i= 5∠60° =0.149∠-3.4°A Z 33.54∠63.4° 0r=Ri=15×0.149∠-3.4°=2.235∠-3.4°V 0L=joLi=56.5∠90°×0.149∠-3.4°=8.42∠86.4°V =jC1=26.5∠-90x0149∠-34=395∠-93 则i=0.149√2c0s(o1-3.4°)A 4r=2.235√2cos(wt-3.4)V U 41=8.42/2cos(ot+86.6°)V -3.4° uc=3.95V2c0s(wt-93.4)V UR 注 U1=8.42>U=5,分电压大于总电压。 相量图
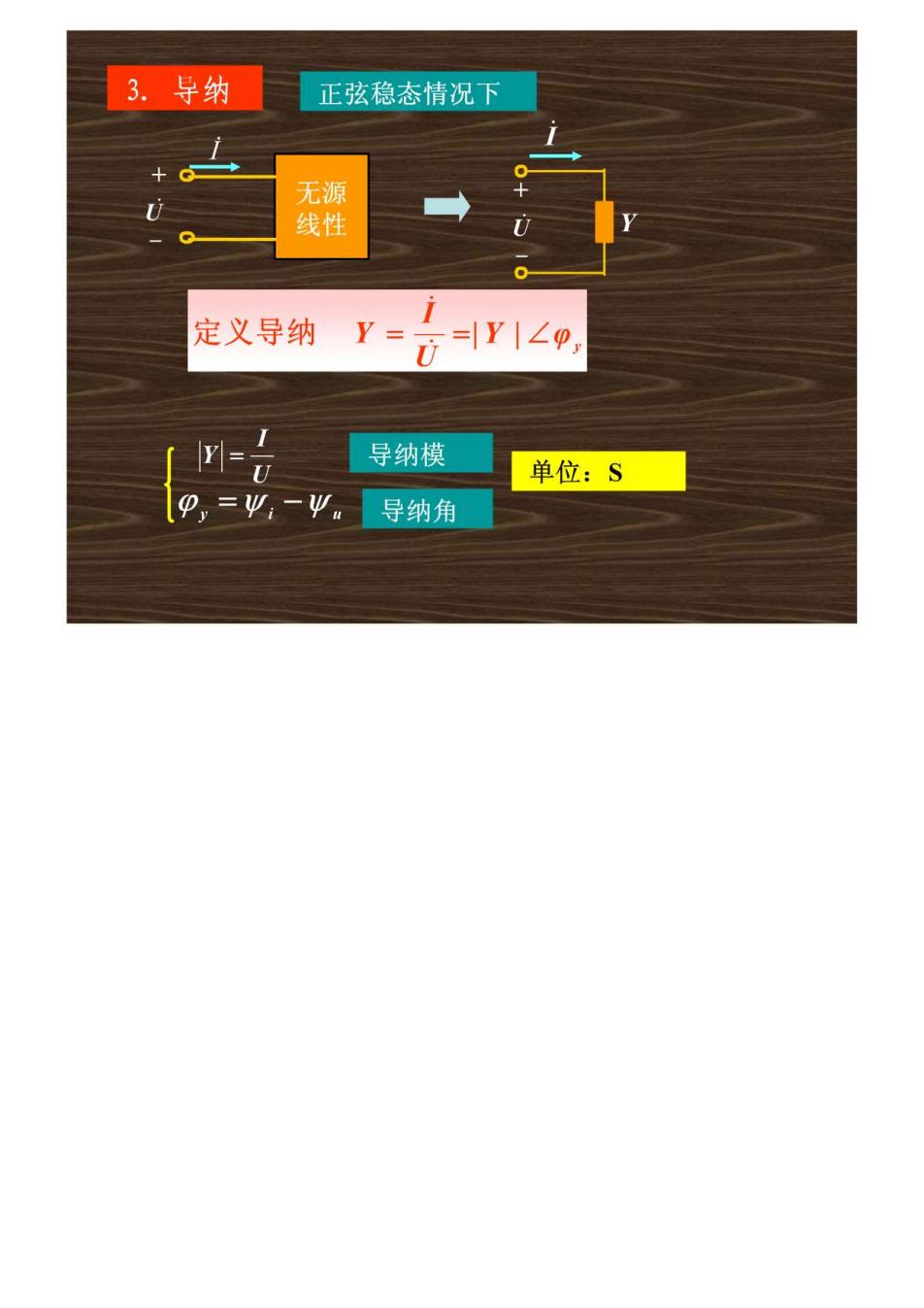
3.导纳 正弦稳态情况下 无源 线性 定义导纳 Y-U =|Y1∠p 导纳模 单位:S 导纳角