
第七章一阶电路 重点 1.动态电路方程的建立及初始条件的确定; 2.一阶电路的零输入响应、零状态响应和 全响应求解 3.稳态分量、暂态分量求解; 4.一阶电路的阶跃响应和冲激响应
第七章 一阶电路 2. 一阶电路的零输入响应、零状态响应和 全响应求解; ⚫ 重点 4. 一阶电路的阶跃响应和冲激响应。 3. 稳态分量、暂态分量求解; 1. 动态电路方程的建立及初始条件的确定;
7.1动态电路的方程及其初始条件 1.动态电路 含有动态元件电容和电感的电路称动态电路, 特点: 当动态电路状态发生改变时(换路)需要经 历一个变化过程才能达到新的稳定状态。这个变 化过程称为电路的过渡过程。 例 电阻电路 i=Us/R i=Us/(R+R) 0 过渡期为零
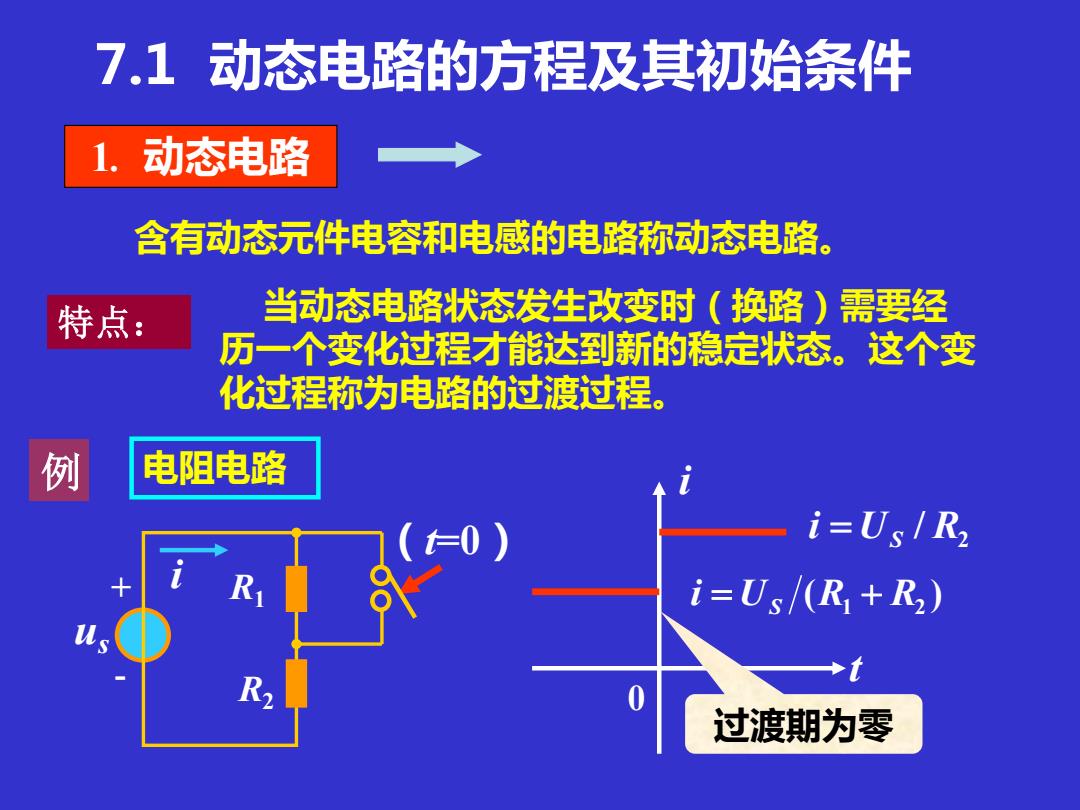
含有动态元件电容和电感的电路称动态电路。 特点: 1. 动态电路 7.1 动态电路的方程及其初始条件 当动态电路状态发生改变时(换路)需要经 历一个变化过程才能达到新的稳定状态。这个变 化过程称为电路的过渡过程。 例 + - us R1 R2 (t=0) i 0 t i 2 i = US / R ( ) U R1 R2 i = S + 过渡期为零 电阻电路
电容电路 K未动作前,电路处于稳定状态 i=0,uc=0 K接通电源后很长时间,电容充电 完毕,电路达到新的稳定状态 t→∞ i=0,uc=Us 前一个 c八 t1新的稳定状态 有一过渡期 过渡状态
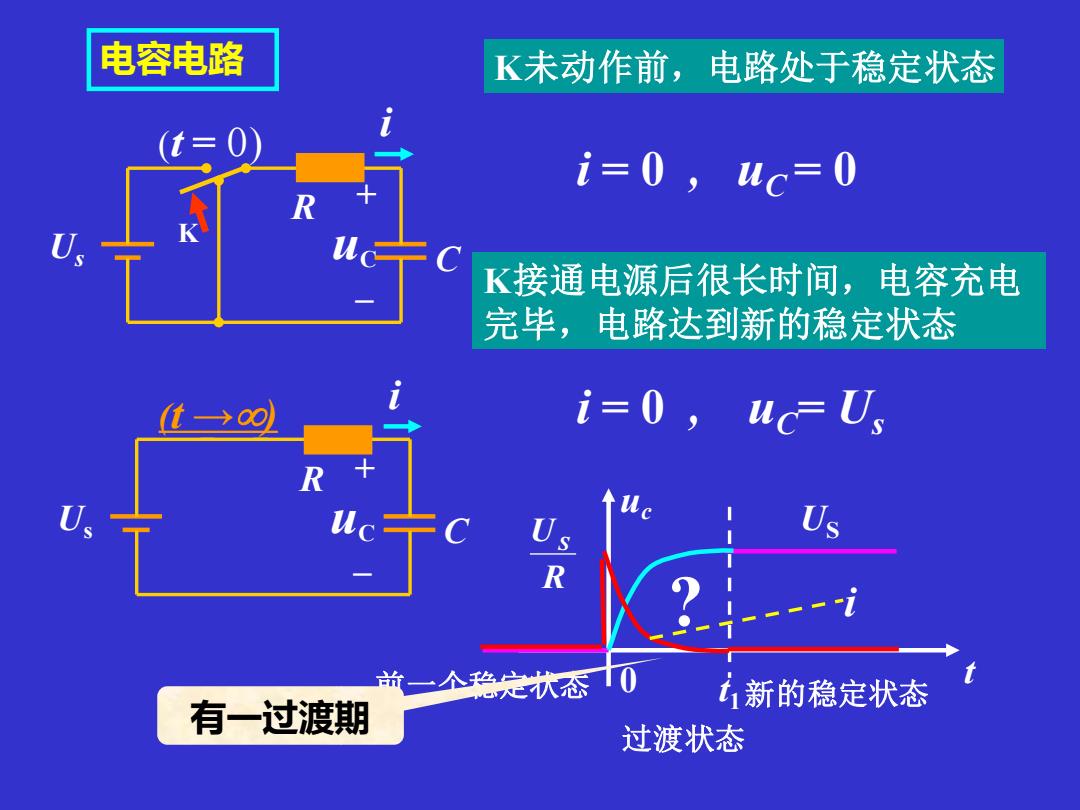
K未动作前,电路处于稳定状态 i = 0 , uC = 0 i = 0 , uC= Us K + – Us uC R C i (t = 0) K接通电源后很长时间,电容充电 完毕,电路达到新的稳定状态 + – Us uC R C i (t →) 前一个稳定状态 过渡状态 t1新的稳定状态 US uc 0 t ? i R US 有一过渡期 电容电路
电感电路 K未动作前,电路处于稳定状态 i=0,uz=0 K接通电源后很长时间,电路达到 新的稳定状态,电感视为短路 →00 u=0,=U、R Us/R 有一过渡期 前一个稳定状态 新的稳定状态 过渡状态
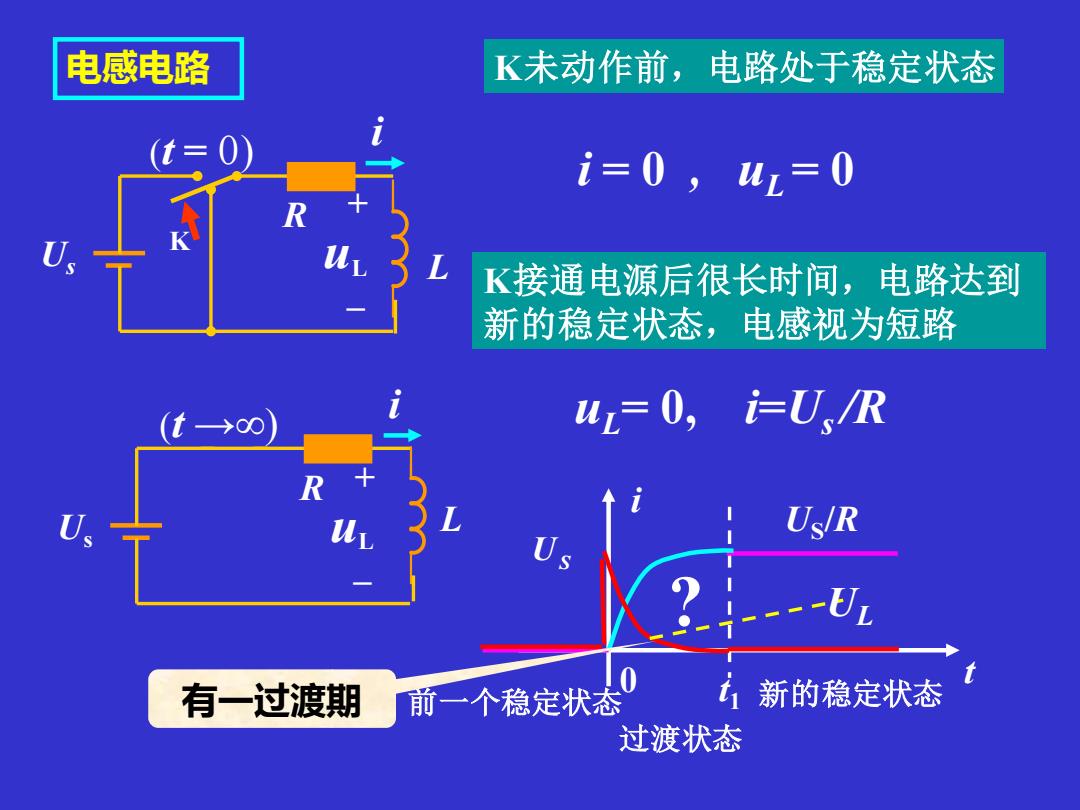
K未动作前,电路处于稳定状态 i = 0 , uL = 0 uL= 0, i=Us /R K接通电源后很长时间,电路达到 新的稳定状态,电感视为短路 前一个稳定状态 过渡状态 t1 新的稳定状态 US /R i 0 t ? UL US 有一过渡期 K + – Us uL R L i (t = 0) + – Us uL R L i (t →) 电感电路
换路 电路结构、状态发生变化 支路接入或断开 电路参数变化 过渡过程产生的原因 电路内部含有储能元件L、C,电路在换路时能量发生 变化,而能量的储存和释放都需要一定的时间来完成。 \W △t→0 00 △t
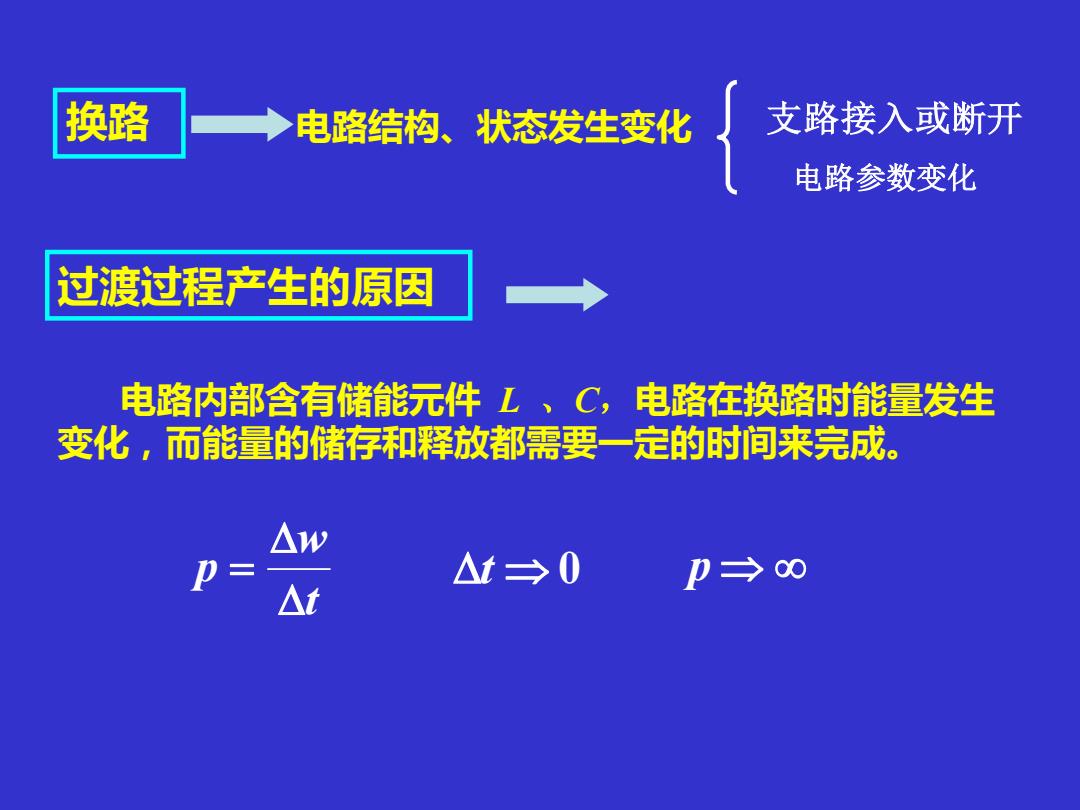
过渡过程产生的原因 电路内部含有储能元件 L 、C,电路在换路时能量发生 变化,而能量的储存和释放都需要一定的时间来完成。 t w p = 换路 电路结构、状态发生变化 支路接入或断开 电路参数变化 t 0 p
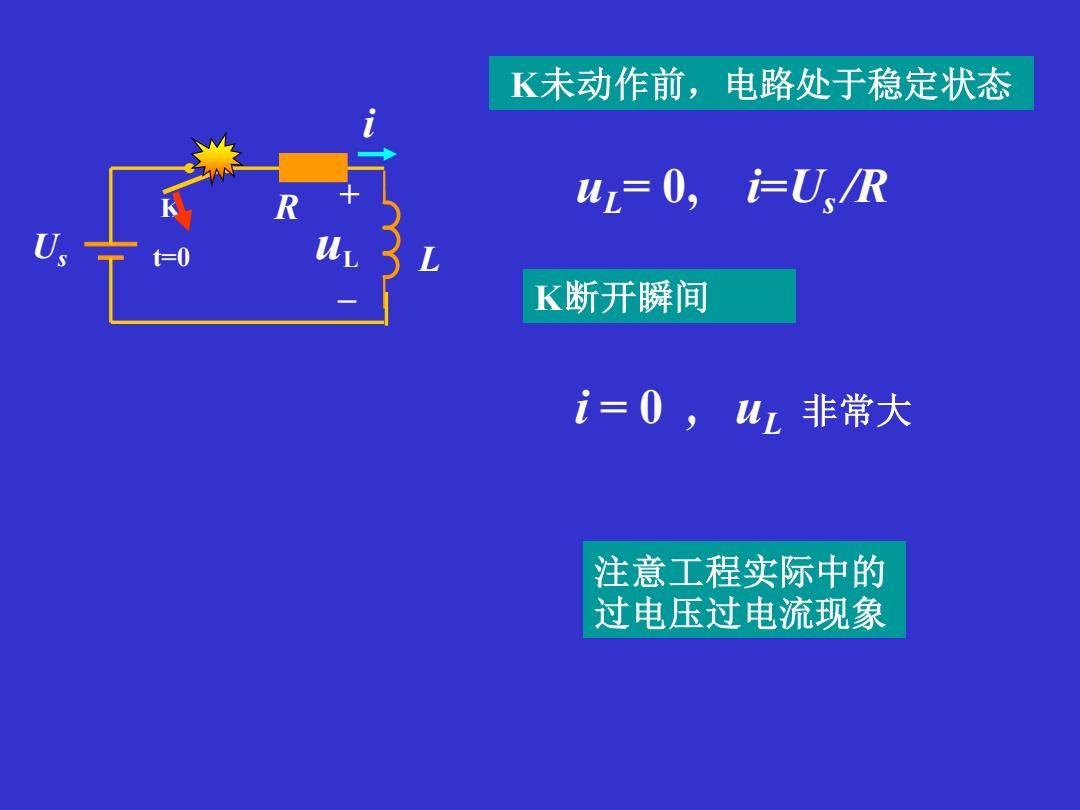
K未动作前,电路处于稳定状态 uz=0,i=U、R =0 K断开瞬间 i=0,uz非常大 注意工程实际中的 过电压过电流现象
K未动作前,电路处于稳定状态 i = 0 , uL 非常大 uL= 0, i=Us /R K断开瞬间 K t=0 + – Us uL R L i 注意工程实际中的 过电压过电流现象
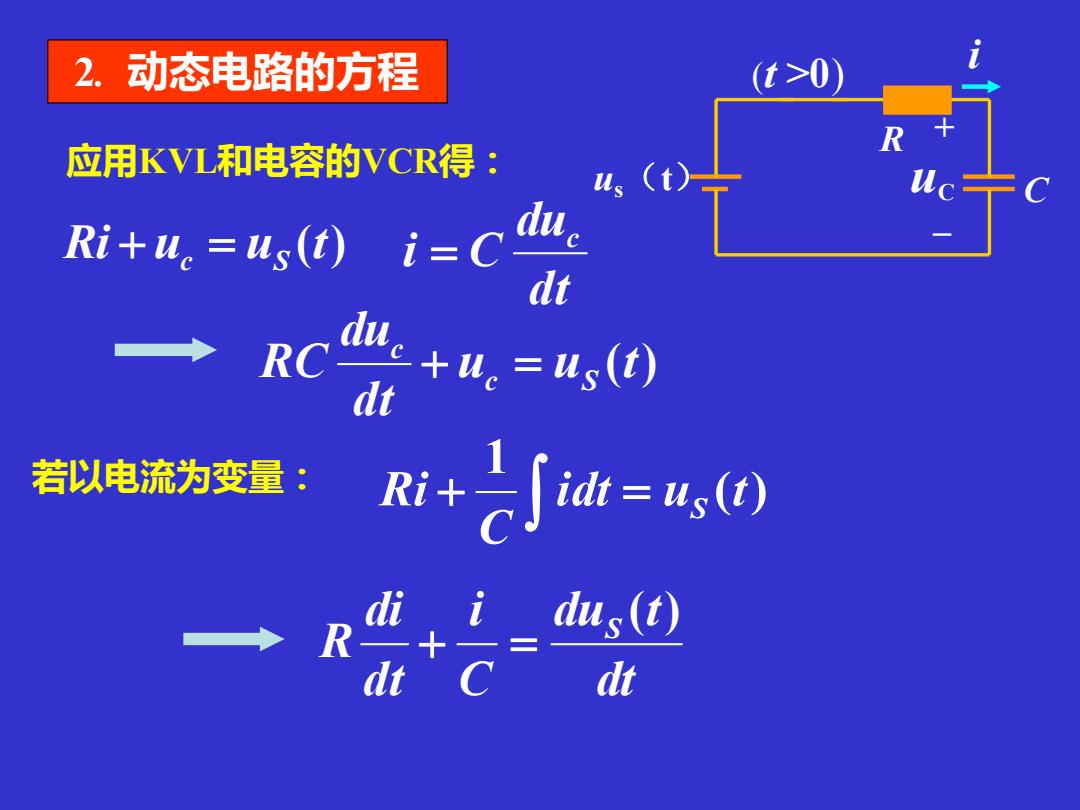
2.动态电路的方程 (t>0) R 应用KVL和电容的VCR得: Riu.=us(t)i=C dt →RC血+u.=a,d) dt 若以电流为变量: +之Jh=a切 d。 i R dus(t) dt C dt
u u (t) dt du RC c S c + = Ri u u (t) + c = S 应用KVL和电容的VCR得: dt du i C c = 若以电流为变量: ( ) 1 idt u t C Ri + = S + – uC us(t) R C i (t >0) dt du t C i dt di R S ( ) + = 2. 动态电路的方程
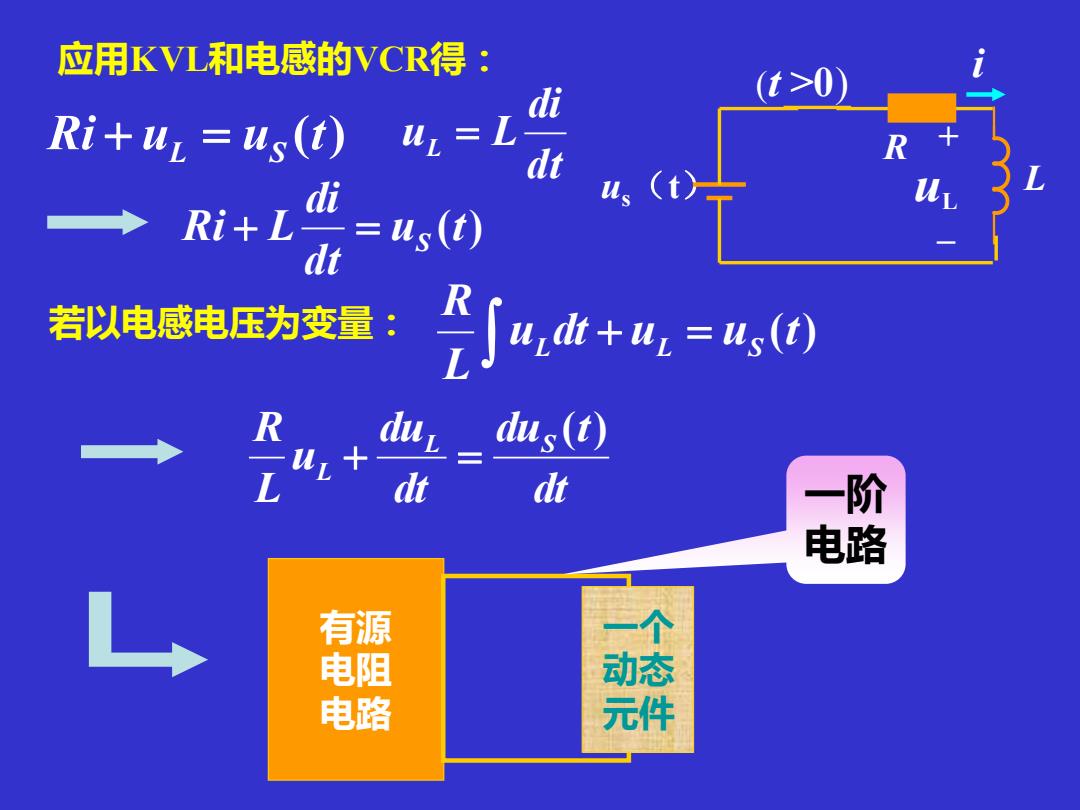
应用KVL和电感的VCR得: d (t>0) Ri+ul us(t)ul L dt R di (t ◆ Ri+L=us (t) dt 若以电感电压为变量: 于+=风 R du= us(t) L z+ dt dt 一阶 电 L 有源 电阻 动态 电路 元件
+ – uL us(t) R L i (t >0) Ri u u (t) + L = S u (t) dt di Ri + L = S 有源 电阻 电路 一个 动态 元件 一阶 电路 应用KVL和电感的VCR得: dt di uL = L 若以电感电压为变量: u dt u u (t) L R L + L = S dt du t dt du u L R L S L ( ) + =

Ri+ul +uc us (t) (t>0) i=Cdue R u,=L us (t dt dt 一C+c路= C 二阶电路 若以电流为变量:Ri十L di dt 之w=0 di R +L- dus(t) dt r+c
+ – uS( uL t) R L i (t >0) C uC - + + - ( ) 2 2 u u t dt du RC dt d u LC c S c c + + = Ri u u u (t) + L + c = S 二阶电路 dt du i C c = dt di uL = L 若以电流为变量: ( ) 1 idt u t dt C di Ri + L + = S dt du t i dt C d i L dt di R S 1 ( ) 2 2 + + =

结论: 描述动态电路的电路方程为微分方程 阶电路 一 阶电路中只有一种动态无件描述 电路的方程是一阶线性微分方程。 d +aox=e(t)t≥0 dt 二阶电路 二阶电路中有两种动态无件,描述电 路的方程是二阶线性微分方程。 d'x dx dt" +ax=e(t) t≥0
一阶电路 一阶电路中只有一种动态元件,描述 电路的方程是一阶线性微分方程。 结论: 描述动态电路的电路方程为微分方程 1 + a0 x = e(t) t 0 dt dx a ( ) 0 2 1 0 2 2 + + a x = e t t dt dx a dt d x a 二阶电路 二阶电路中有两种动态元件,描述电 路的方程是二阶线性微分方程