
第8章 相量法 重点: 1.正弦量的表示、相位差; 2。正弦量的相量表示 3.电路定理的相量形式;
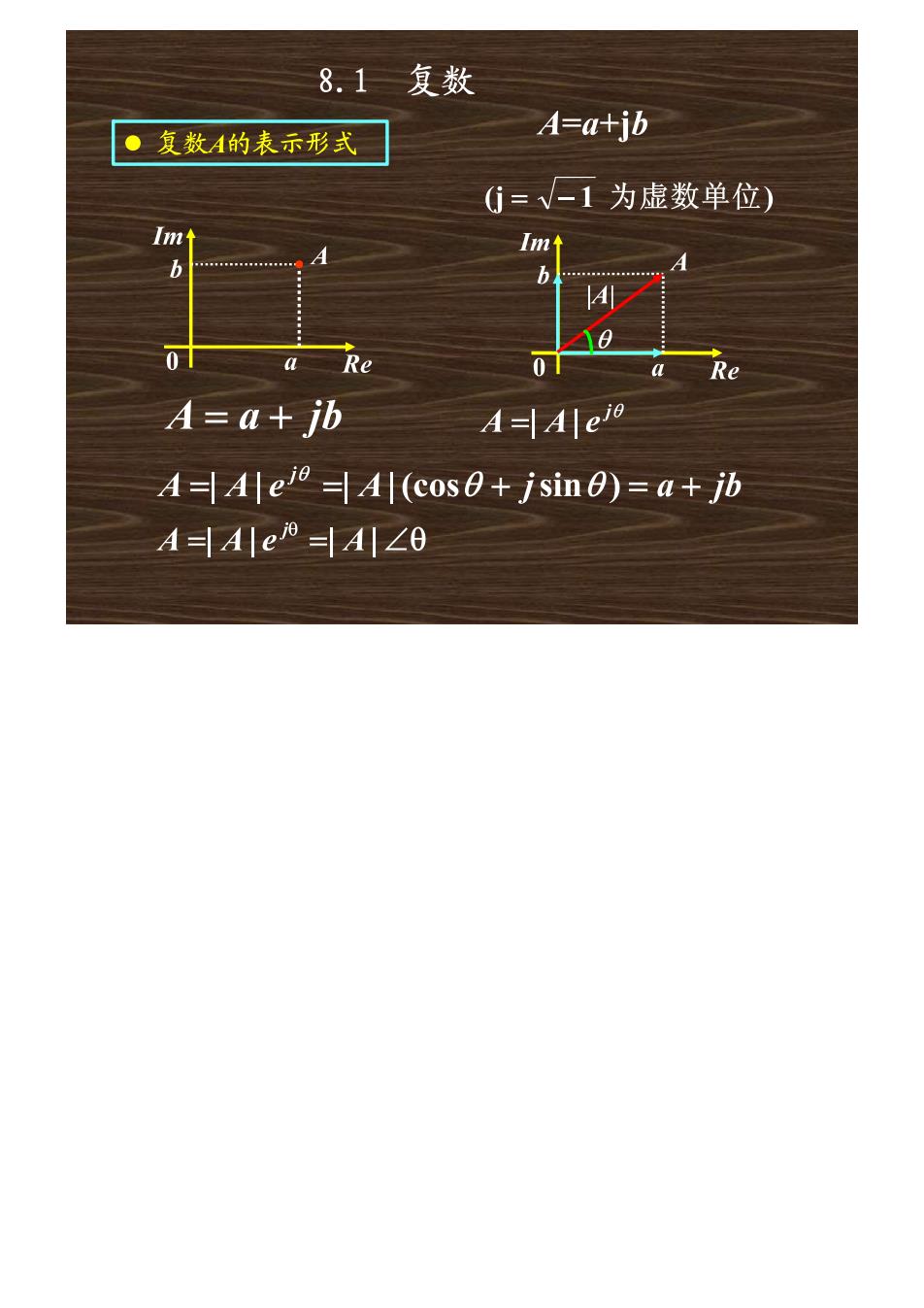
8.1复数 ·复数A的表示形式 A=a+jb G0=V-1为虚数单位) Im Im个 b b 01 Re 0 a Re A=a+jb A=Aleio A=Ale=Al(cos0+jsin0)=a+jb AHAe|A4|∠0
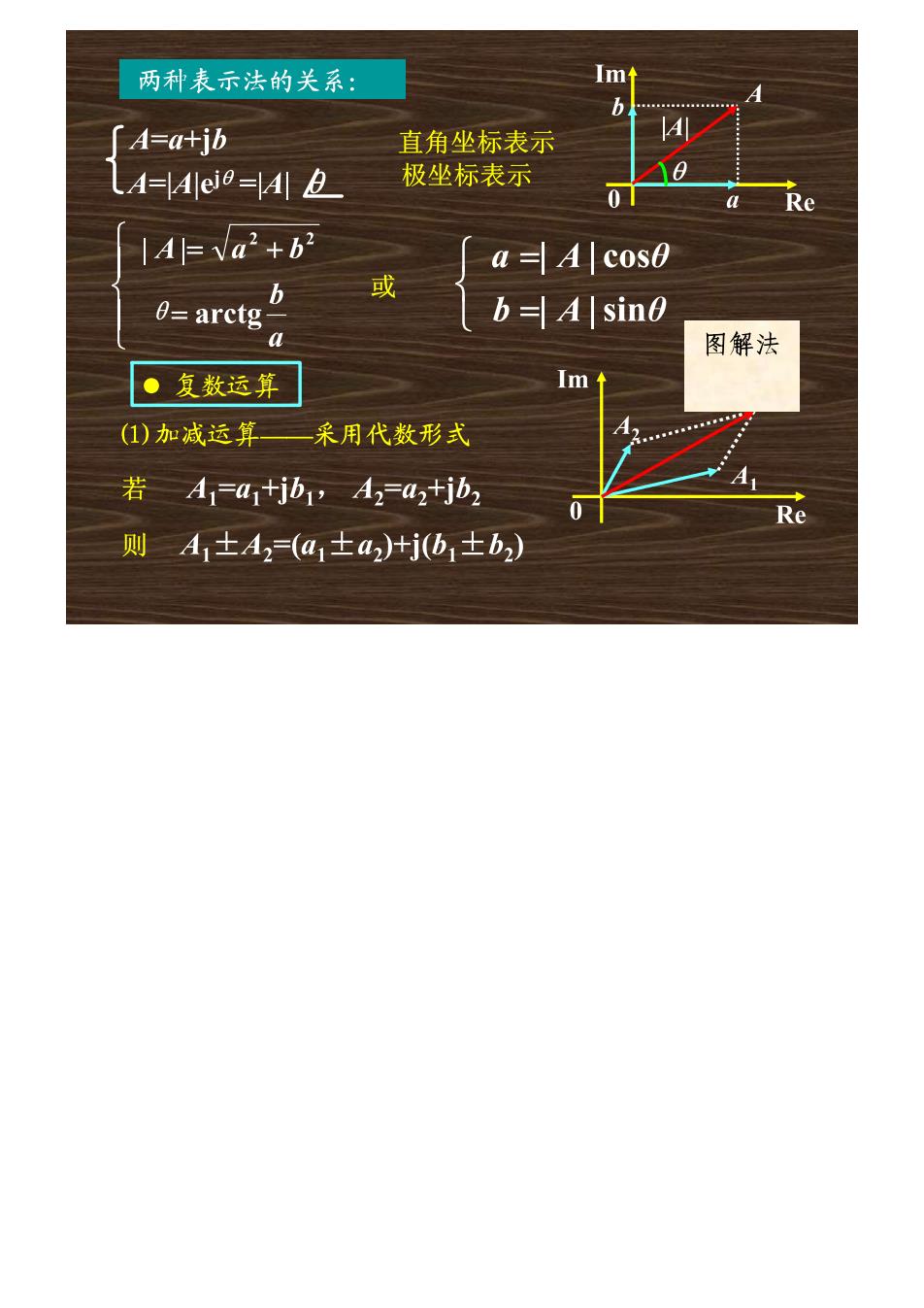
两种表示法的关系: b 「A=a+jb 直角坐标表示 LA=Aleio=A0 极坐标表示 0 Re |A =va2+62 a =A coso 或 0=arctg b=A sine a 图解法 ·复数运算 Im t (1)加减运算 采用代数形式 若A1=a1tjb1A42a2tjb2 Re 则A1±A2(a1±a2)+j(b1b2)

(2)乘除运算— 采用极坐标形式 若AAl/01,A2AlB2 则:AA,=4e84e8.=44e8+ =AA2∠0+02 乘法:模相乘, 角相加。 A=141∠01=|Ale ej01-02) A2A∠03 |A,|e02 A, 01-02 除法:模相除, 角相减。 A2 例1.5∠47°+10∠-25°=? 解 5∠47°+10∠-25°=(3.41+j3.657)+(9.063-4.226 =12.47-j0.569=12.48∠-2.61

例2. 220∠35°+ (17+j9)(4+j6) 20+j5 解 原式=180.2+j126.2+19.24∠27.9×7.211∠56.3 20.62∠14.04 =180.2+i126.2+6.728∠70.16 =180.2+126.2+2.238+j6.329 =182.5+j132.5=225.5∠36 Im A·ej0 (3)旋转因子: 0 复数ej0=cos0+jsin0=1∠0 0 Re A·ej8相当于A逆时针旋转一个角度0,而模不变。 故把e称为旋转因子

几种不同0值时的旋转因子 m 0= 2 Re 2 9=-e-os+jm-7- 0=土元,er=c0s(仕π)+jsin(仕元)=-1 故+i,一i,一1都可以看成旋转因子

8.2正弦量 1.正弦量 W/o 瞬时值表达式: 波形: i()=lmc0s(ot什の 正弦量为周期函数)=∫(什kT) 周期T(period)和频率f(frequency): f生 周期T:重复变化一次所需的时间。 单位:8,秒 频率f:每秒重复变化的次数。 单位:Hz,赫(兹)

●正弦交流电路 激励和响应均为正弦量的电路 (正弦稳态电路)称为正弦电路 或交流电路。 研究正弦电路的意义: (1)正弦稳态电路在电力系统和电子技术领域占有十分重 耍的地位。 优点: 1)正弦函数是周期函数,其加、减、求导、积分 运算后仍是同频率的正弦函数 2)正弦信号容易产生、传送和使用

(2)正弦信号是一种基本信号,任何变化规律复杂的信号 可以分解为按正弦规律变化的分量。 f)=∑Acos(kot+0) k=1 对正弦电路的分析研究具有重耍的理 论价值和实际意义

2.正弦量的三耍素 i(t)lmc0s(ot什叨 (1)幅值(amplitude)(振幅、 最大值)Im 反映正弦量变化幅废的大小。 (2) 角频率(angular frequency)o 相位变化的速度,反映正弦量变化快慢。 0=2rf=2r 单位:rad/s,弧度/秒 (3)初相位(initial phase angle)y 反映正弦量的计时起点, 2元 常用角度表示